Бугай П.Т. Теорія помилок і спосіб найменших квадратів

Подождите немного. Документ загружается.

або, розкривши дужки і звівши подібні члени по (х), (у),

(z)

-----

(и),

F = F0 -і- [al]q1 -b[bl]qs + [cl]qt + .. . 4 [tl)qk -\,

■b {[aajg'i 4- \ab]q2 -I- [ac}q.A +... + \at]qk +/і}(х) -|-

+ {[ab}qi + [bb]q2 -b [bc]qx +... + [Ы]дкл'/,}(у) + (56,9)

-\{[at}ql + [bt]q<Mct]q.i + ... + {tt}qk-bfk}{u).

Підберемо тепер неозначені множники qt, q2, . . . qk так,

, щоб вирази в фігурних дужках дорівнювали нулю, тобто

припустимо, що

\aa]ql + [ab]q2 + [ac}q?i +. .. f \at}qk Л /, 0,

[ab}qi^[bb\q2 + {bc]q;i +. . . + [bt}qk+f2~0t

[ac\q^-{bc)q2-{-\cc\qz^-... + \ct]qkJrfs^ О, (56,10)

jai\q1 + fhi]q2 + 1ct\qVi + ... + [tt\qk-\ f lt- 0 .

Тоді попередній вираз (56,9) можна записати так:

F /-’0 + [а/]<7і -I \bl\q2 + [ cl] q., +. . .-I \tl\qk. (56,11)

Тепер вагова функція F виражена через незалежні між

собою величини /і, h, ■■■, Іп, і до неї можна застосувати

формулу (56,8) для визначення оберненої величини ваги,

функції:

Рр Ь \дй ! '

і~ 1

де п - - кількість вимірів.

Огже, знайдемо часткові похідні функції (56,1)). Для

цього запишемо її в розгорнутому виді:

F=F0 \ ] 11 'і" а212 ■ і' (і з “і . * ■ -Ь Сї /; ) q j “ *

І {^1^1 + ьм~Ь Ь-лІг + .. . bJ„}q2Jr

"І" ^ > "1' І?. і . ■ • -і- c„ln}q3 +

~І {^1^1 4 ^0/3 "і'^3/3 4 •

і продиференціюємо по величинах /ь /2, ..., U :

—• = art і -Ь Ь^2 -і- од*, +... + txqk,

W: ” a^i -і' ьгЯг + С-Яг 4-... + Uqk, ,

д ї, “ + &з?з + с ъЧг + • ■ ■ + t 3 q kt

* — &nQі \~^пЦ% Л'СпЦъ . • • . tnQk'

Uln

Знайдемо тепер, згідно з формулою (56,8), суму квадратів

цих часткових похідних. Додаючи до неї величини fiqu f2q2,

■ ■ ,fk4k і одноразово віднімаючи їх, будемо мати:

р~ - (М <7і + [ab]q3 -і- [ac]q9 + ... + [at]qk +

+ {И]<7і + [*%а + [^Фз + ■ • - + [bt\qk + f 2)q2 +

\ - t[ac]qi + lbc]q2-\-[cc\ q9 I■. . . \ [ct]qk + / 3}?8 +

...........................

........................................................ (56,13)

r^_ctt]qlJr[bt]q2 + [ct\qz +. . . + [tt]qk-\fk}qk —

fb4% * • • 'fkQk-

Але, згідно з (56,10), вирази у фігурних дужках дорів

нюють нулю. Через те

~ p - - f lql+f2g3+f3q3 +.. .+fkqh. (56,14)

Ця формула і служить для визначення оберненої величи

ни ваги функції врівноважених аргументів х, у, z, , и. В

ній величини /і, /2, /я, ■ . . , fk — часткові похідні функції.

Множники q

і,

q2,

....

qk називаються перехідними кое

фіцієнтам и. Вони визначаються із системи рівнянь

(56,10).

Легко прослідкувати, що якби виміри були проведені не-

рівноточно, тоді неозначені множники q\, q2, . . ., qu визнача

лися б з таких рівнянь:

[paa\ql^-[pab}q2 + {Pac\q% + ■ ••!-[)vat]qk +/j = О,

[pab\ql + [pbb]qr \-[pbc\q3 + . . . +{pbt)qk + f2 = 0,

[pac]q^{рЬс^^-Ірсс^яЛ- ... + [pct]qk+fs = 0, (56,15)

[patjqy + [pbt]q2 + [pct]qs + ... + [pit }qk+ /* = 0,

а формула (56,14) для визначення оберненої величини ваги

функції залишалася б незмінною.

Розглядаючи системи рівнянь (56,10) і (56,15), бачимо,

що вони відрізняються від нормальних рівнянь лише віль

ними членами та назвою невідомих. Коефіцієнти ж при неві

домих однакові. Через те перехідні коефіцієнти q\, q2, . . . , фі-

можна визначити в .схемі Гаусса—Дулітля (а також і в ін

ших схемах) разом з розв’язанням .нормальних рівнянь. Для

цього в схему треба вставити додатковий стовпчик /. Якщо в

цей стовпчик ми будемо виписувати величини /ь f2, .. -, fk і

проводитимемо з ними ті ж самі операції, що й з вільними

членами нормальних рівнянь, то в результаті одержимо ве

личини ди Ці, ■ ■ •, Яь ■

§ 57. ВИЗНАЧЕННЯ ВАГИ ФУНКЦІЇ

ВРІВНОВАЖЕНИХ ВЕЛИЧИН ЧЕРЕЗ ВЕЛИЧИНИ f{

1 КОЕФІЦІЄНТИ ЕКВІВАЛЕНТНИХ НОРіМАЛЬНИХ РІВНЯНЬ

Для визначення оберненої величини ваги іфункці-ї перехід

ні коефіцієнти q, можна і не обчисляти, а величину -д- мож-

на виразити в функції величин fi, /2, . .., fk і коефіцієнтів ек

вівалентних нормальних рівнянь. Щоб показати це, візьмемо

систему рівнянь

[aa] (/j і- \ab\q, + [ас] q^+fi^O,

[ab] </i Ч- [bb]q.,+ [bc] </;,+/;> = 0, (57,1)

[ac] </,+ [be] q, \- [cc] <73+/» = (),

яка відповідає функції лише трьох врівноважених величин,

і розв’яжемо її методом послідовного виключення невідо

мих.

Визначимо з першого рівняння (57,1) невідоме q\ і під

ставимо його в друге і третє рівняння. Послідовно будемо

мати:

^ = - f S | ^-[аа] (1~[аа\' (57,2)

Ь [bb] q-> + [be] qs -t- /2 = 0 ,

+[Ьс\ <?2+ Н ^ + / з = 0. ■

Розкривши дужки в останніх двох рівняннях, після зведен

ня подібних членів одержимо:

\ т

} „ + {їм - W ».+ {л-да-о.

(57,3)

f/,r | — 1/7 a f <rr\ N M ] ( f Мас]\ п

' * йГаТ I ^

-------

Ш ~ /?» f \ Л - Таа] І = °'

205.

Вирази у фігурних дужках при q2 і qz відповідно рівні

[ЬЬЛ], [be. 1], [ЬсЛ] і fcc.ll. Крім того, введемо такі позна

чення:

1],

J " ялі LJ - J

(57,4)

f L_ r f . і і

/ з \aa] V*

Тоді рівняння (57,3) можна записати так:

[bb-1] q2+ [be-1] 9,-!- [/,• 1] = 0,

[beA] q-2+ \ccA] ?,+ l /s - l] - 0.

(57,5)

Знайдемо тепер з першого рівняння системи (57,5) неві

доме q2 і підставимо його в друге:

____

_ _ IA iL L /57 5)

<?3“ [M -ips Ibb-l]’ 10/,о;

11 ( — тйттт^з—[Йгіг) + Г^-1]^з-Ь[Л-1] “ 0. .(57,7)

або

/ f/v>. 1 1 №c-l] [fo- Ч j, . 1 / [у- -11

ІЛ’ 1 і 1^С~ Ч 1 _п (К7

Ч [б*.і] ) Я-л і ( l/з Ч [М-1] j и. (о/,8)

Вираз у першій фігурній дужці дорівнює [сс.2]. Для ви

разу у другій дужці введемо позначення

( 5 7 ’9 )

Тоді рівняння (57,8) запишемо в такому вигляді:

[сс-2]д3Л [Л-2]«0. (57,10)

Таким чином, початкову систему рівнянь (57,1) ми пере

творили в таку еквівалентну їй систему:

[аа] q{+[ab] q2 + [ас] qa + /,=-0.

[bb-1] q2-f [be-1] q.,+ [fr 1] =0, (57,11)

[cc-2] qz-V [/3-2] = 0 .

З останнього рівняння знаходимо значення перехідного

коефіцієнта <7з:

і. С57 і О)

Чя [сс-2] '

Підставивши його в (57,6), знаходимо:

[ЬсЛ] [/з -2] [/,•!]

[ab] fftc-І] [/а-2] [ab\ [ /,; 1J [ас] [/,■ 2] _Л /с 7 , 4 ч

[ля] [6й-1 j [сс-2] ]аа][<Ь6-1] [аа] [сс - 2] [аа]' ^ '

Коефіцієнти qt потрібні нам для визначення оберненої ве

личини ваги наперед заданої функції. Через те підставимо

їх значення (57,2), (57,6) і (57,12) в загальну формулу

(56,14):

_ [fo-nt/ii-Sl . /іИПЛ-М , /іІде] 1/з-2]

Р{, [аа] [яя] [W -l] [сс-2] ^ [яв] [66-1] "Г [аа] [cc-2j +

,/,[*с-1][Лі2]_ ЛГ/,-1] , /,[/»• 2]

f [6й-1 j [сс-2] “ '[&];• 1] ^ [сс-2] ’

або

І_= —Л і j 16с~і1 [/з- / f _ _ /іИ 1 'і / f _ /Лас1 )

[л а Г [йй-1] [сс-2] І / - [аа] / [сс-2] [аа] /.

__ !/•••'-! / г _ Л И \

Ігс -2] [яя] /•

Беручи до уваги введені раніш для виразу у круглих

дужках позначення (57,4), останнє, рівняння можна записа

ти так:

L = _ / і а 4 1^-і][Л-1]|/,-2] |/з-1] [/а-2] ІЛ-1)

PF [ааУ [bb-1] [сс-2] [сс-2] [bb-1] ’

або

J L

___

Л1__ЇЛ-П " ІЛ-21/rx ,, [fo -in / ,-in 3

Рр [аа] [bb-Ц [сс-2] 1 J [66-1]

Але, згідно з позначенням (57,9), вираз у дужках дорів

нює [У.і.21, а тому одержимо таку остаточну формулу:

(57,15)

Ри [аа] [ftft-lj [сс-2] v ’ ’

В загальному випадку функції від k врівноважених аргу

ментів формула для визначення оберненої величини ваги

функції буде така:

» Д + |£ іі; + іб * р + _ (57,16)

Рр [аа] [bb ■ 1] [сс-2]- £fr-(*—1)]

Всі величини, необхідні для обчислення за цією формулою,

одержують в схемі Гаусса—Дулітля, не визначаючи самих пе

рехідних коефіцієнтів <7ь С/2, . - • , Цк •

Формулу (57,15) можна одержати за аналогією так само,

як ми одержували [vv] (див. §50).

Справді, запишемо такі дві системи рівнянь А і В:

Система В

Система А

[aa]х + [ab]y + [ac}z -r[al] = 0,

[ab]x -v[bb]y -і- \bc\z-k-\bl] -=0,

І ас]х+ [Ьс]у + [cc\z + \cl] = 0,

[al\x + [bl]y + [cl]z + [ll}=[vv].

Раніш для системи А ми ма

ли

[vv] = [// • 3]

[сЛ2]г

Ісс - 2]

Допоміжні величини для об

числення [рс>] такі:

[аі],

[ЫЛ}-[Ы]

[аа] qx + [ab] q? + [ас] qt + /, - 0,

[а% ! + [ bb]q2+ [ be] qs + f% = 0,

[ac] ql + [be] 9'а+ М ^ з+ /а = 0 ,

ЛЧі + Л Я 2 +/»Я з + 0 “ - 7 Г -

За аналогією для системи В

можна записати:

- p L = [0-3)

= 0 -

/г , l/,J]s ,

[аа] Г \ЬЬА\ 1

-I-

[/г2р

[сс-2]'

Відповідні їм величини

обчислення

‘ гт

для

\аЬ] [аі]

\аа\ ’

[cl-l]^[el]-[-ac^ ],

\ с і - ^ [ с І Л ] - ^ р .

л,

ІЛ-Ч-Л-

ІЛ -1] Л ,

[/з-2] = [/з-1]

[аа]

./і К 1

Іааі

[/2.Щ 6с.І]

[М-1] ■* •

Порівнюючи останні вирази допоміжних величин, легко по

мітити закон утворення позначень, які ми вводили форму

лами (57,4) і (57,9).

§ 58. ВИЗНАЧЕННЯ ВАГ ОСТАННЬОГО

І ПЕРЕДОСТАННЬОГО НЕВІДОМИХ

Користуючись загальною формулою (57,15), легко знайти

вагу останнього невідомого z (для системи нормальних рів

нянь з трьома невідомими). Для цього припустимо, що ва

гова функція має вид

F(x,y, z)=z.

Для використання формули (57,15) знаходимо її часткові

похідні

/, 0, Л - n, / я 1

(58,1)

і величини

1]~ 1.

(58,2)

Підставивши (58,Г) і (58,2) в (57,15), будемо мати:

(58,3)

тобто вага Рг останнього невідомого z дорів

нює коефіцієнту при цьому невідомому в

о с т а н ньому е к в і в а л е « т н о м у я о р м а л ь н о м у

р І в Н Я II II і.

Легко переконатися в справедливості цього правила і в

загальному .випадку системи нормальних рівнянь при k .не

відомих:

де и — останнє невідоме, a t- коефіцієнти ігри ньому в рів

н ян нях 'ПОМИЛОК.

Так само можна знайти і вагу передостаннього невідо

мого, якщо буде, відома вага останнього невідомого. Для

цього при трьох невідомих припустимо, що вагова функція

має вид

Ра W- {к -1)|,

(58,4)

F(x, у, z) = y.

Знаходимо часткові похідні цієї функції

/ , ~ 0 , / 2~ 1 , / 8~ 0

і величини

------

[**тН-

(58,6)

Підставивши (58,5) і (58,6) в (57,15), одержимо:

Ру [ьь:ц + [ьь.ц'-р/

або, ви нісш и щ ~ ц за ДУж ки,

(58,7)

Але

[ w 2] -[c c l]-{ |0 ,

№ Щ -[сс.1]~[сс.2].' . (58,8)

Підставивши це значення в (58,7), будемо мати:

'Ру ~[ЬЬЛ \ і 1 ' >

або, розкривши дужки, після скорочення на [сс.2] одержимо:

і [СС-1] 1

Ру^\ьь:\\ /у

звідки

P y ^ ^ P z. (58,9)

Як видно з формули (58,3) і (58,9), всі величини, необ

хідні для визначення ваг останнього і передостаннього неві

домих, одержують при розв’язуванні нормальних рівнянь в

схемі Гаусса-—Дулітля.

Визначати таким способом ваги інших невідомих уже не

доцільно, тому що для них будемо одержувати складні ви

рази. Через те астроном Гпке запропонував для визначен

ня ваг дальших невідомих проводити перестановку нормаль

них рівнянь з повторним розв’язуванням їх. Так, наприк

лад, щоб знайти вагу невідомого х, нормальні рівняння не

обхідно записати так:

[сс] z 4- \ Ьс\ у -і- [ас] х + [сі] = 0 ,

\bc\ z+ [bb] y-Y [ab] х+ [bl] — 0,

[йс] z-v [ab\у f [aa] x-\- [al] --=(),

де «езідоме x стоїть на останньому місці. Розв’язуючи їх ме

тодом послідовного виключення невідомих, в схемі ми одер

жали б величину [аа.2], яка дорівнювала б Рх. Але такий

спосіб мало застосовують, тому що існують кращі способи

У геодезичній практиці ваги остатнього і передостанньо

го невідомих доводиться визначати тоді, коли при врівно

важенні тієї чи іншої геодезичної сітки хочуть дати оцінку

точності не всіх її елементів, а лише тих, які найбільш від

далені від вихідних даних. Очевидно, що /точність їх буде

лайм енш о ю , а точність інш их у в сяк о м у разі -не меншою від

точності цих н а й більш віддалених.

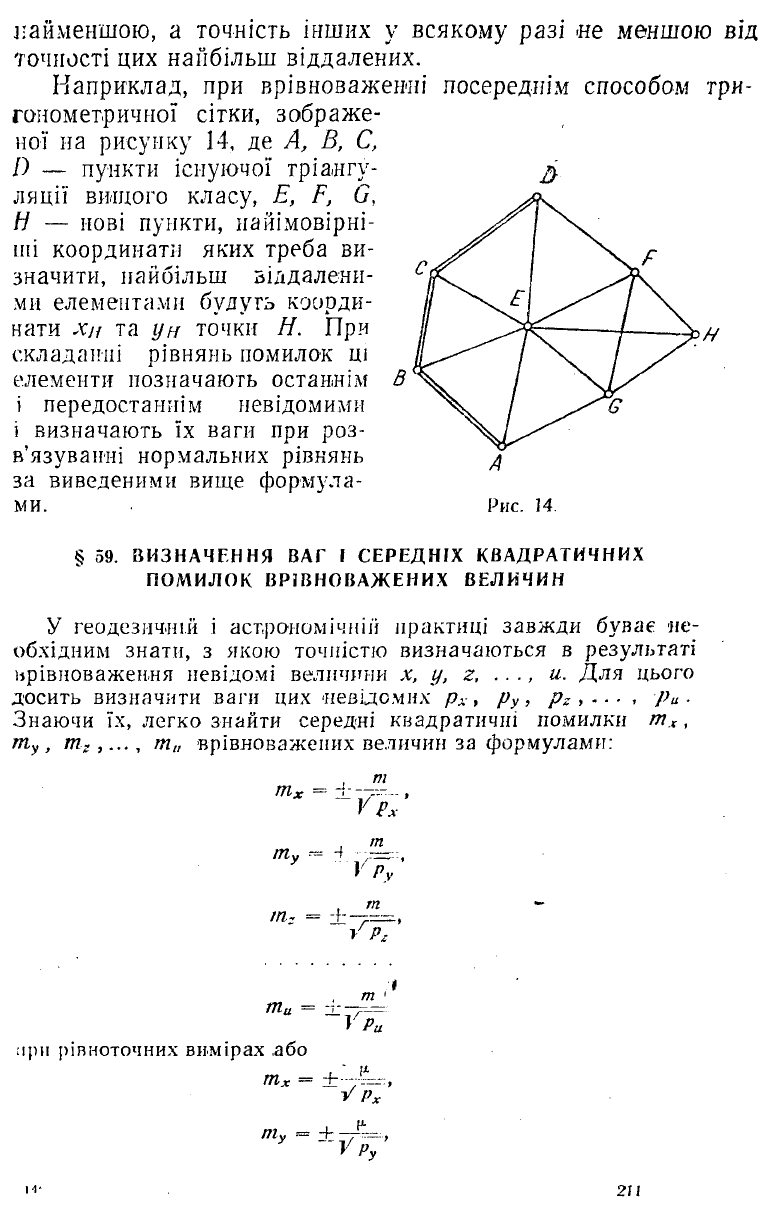
Н а п р и кл а д , при врівн оваж ен н і посереднім способом три

гоном етричної сітки, зо б р а ж е

ної на рисунку 14, де А, В, С,

D — пункти існуючої тріан гу

ляції вищ ого класу, Е, F, G,

И — нові пункти, найім овірні

ші координати яких треба ви 

значити, н айбільш віддалени

ми елем ентами будуть коорди

нати Хц та ун точки Н. П ри

складанні рівнянь помилок ці

елементи позначають останнім

і передостаннім невідомими

і визначаю ть їх ваги при роз

в’язуванні нормальних рівнянь

за виведеними вище ф орм ула

ми. Рис. 14.

§ 59. ВИЗНАЧЕННЯ ВАГ І СЕРЕДНІХ КВАДРАТИЧНИХ

ПОМИЛОК ВРІВНОВАЖЕНИХ ВЕЛИЧИН

У геодезичній і астрономічній практиці завжди буває не

обхідним знати, з якою точністю визначаються в результаті

врівноваження невідомі величини х, у, z, ..., и. Для цього

досить визначити ваги цих 'невідомих рх , ру, Pz , - ■ • . Pu ■

Знаючи їх, легко знайти середні квадратичні помилки тх ,

ту, тг ,..., т„ врівноважених величин за формулами:

тх == :г

У Рх

V Ру

І т

т~ = -±-у.=.

У Рг

ти =

ари рівноточних вимірах ,або

'V ~ P u

тх = ± .■,

У~Рх

...

якщо виміри нерівноточні. Середні квадратичні помилки од

ного виміру т і одиниці ваги jx знаходять за відомими фор

мулами

де k — кількість невідомих, а п — кількість вимірів.

Визначити ваги врівноважених величин можна двома спо

собами: за допомогою так званих вагових коефіцієнтів і ко

ристуючись загальною формулою (56,14) для визначення

оберненої величини ваги функції врівноважених величин.

Перший спосіб. Для визначення ваг невідомих, які ми

одержуємо, розв’язуючи нормальні рівняння, необхідно кож

не з невідомих х, у, .... и виразити в функції величин /,• —

— (х0, уо, .. ■, Uo) — L;, які мають таку саму середню квад

ратичну помилку, що й безпосередньо виміряні величини L,.

Це можна зробити за допомогою неозначених множників так.

Нехай маємо систему нормальних рівнянь, припустивши

спочатку, що посередні ниміїри були проведені рівноточно:

Іаа\ х \ \ab\ у + \ас\ z ь ... ь \ at \ и !- [al\ = 0 ,

[ab] x+\bb\y +- [bc\ z + ... + [bt\ u+[bl[=0,

[ac\ x+[bc] у \-{cc\ z-\-...-v[ct] и+[с/]= 0,

Помножимо їх на неозначені іпоки що множники: перше

рівняння на Qn, друге — на Qi2, &-ве рівняння — на Qік

і добутки складемо:

{\аа\ х+ [ab] у-і- [ас] [at] и+ [a/]}Qu +

+ {[ай] x+[bb]y + [bc] z + .

+ {|tff] x+ [be] y+ [cc[ z к

+ [bt\ U+ [6/]}Qi2 +

\ [ct] u \- [c/j}Qls-f