Бугай П.Т. Теорія помилок і спосіб найменших квадратів
Подождите немного. Документ загружается.


Тайлиц я 33
Номери
ХОДІВ
Виміряні пе
ревищення Л
в м
Донжипи
ході в
11 км
1
Номери І
ходів
Виміряні пе
ревищення h
в м
Довжини
ходів
в км
1 + 10,808
24,2 5
-І ■ 14,381
21,2
о
’ 7,912
10,8
6
- 16,302
12,5
3 ■і~ 31,182
13,4
7
-і 8,914
9,3
4
-і- 14,894
14,9
8
+ 24,286
7,1
В
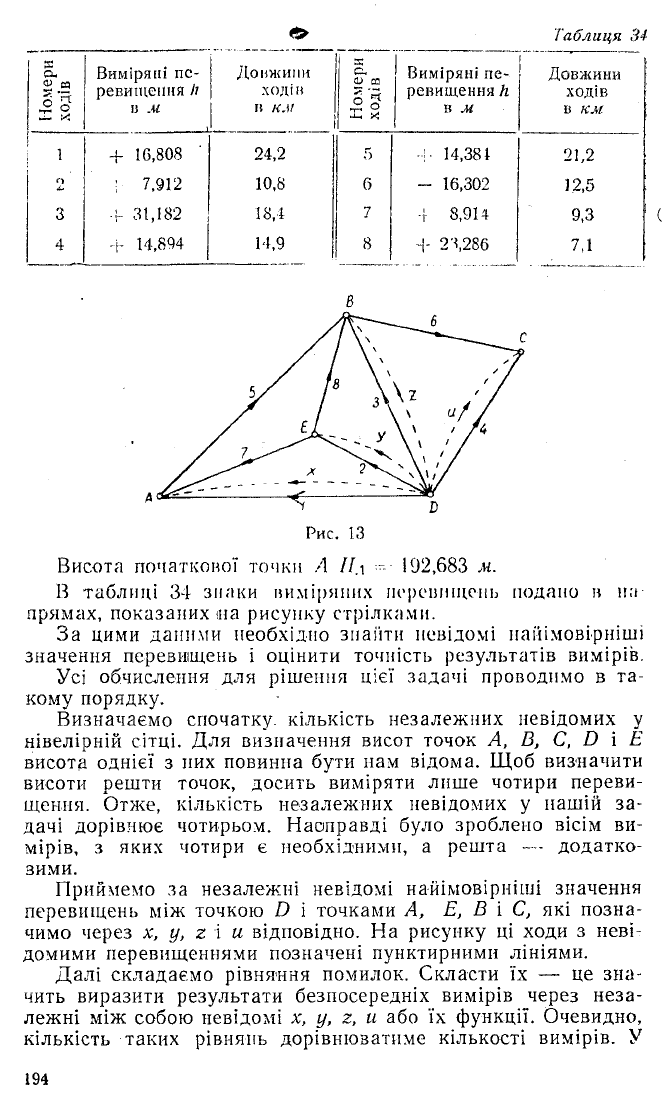
Рис. 13
Висота початкової точки А П.\ ----- 192,683 м.
В таблиці 34 знаки виміряних перевищень подано в на
примах, показаних «іа рисунку стрілками.
За цими даними необхідно знайти невідомі найімовірніші
значення перевищень і оцінити точність результатів вимірів.
Усі обчислення для рішення цієї задачі проводимо в та
кому порядку.
Визначаємо спочатку, кількість незалежних невідомих у
нівелірній сітці. Для визначення висот точок А, В, С, D і Е
висота однієї з них повинна бути нам відома. Щоб визначити
висоти решти точок, досить виміряти лише чотири переви
щення. Отже, кількість незалежних невідомих у нашій за
дачі дорівнює чотирьом. Насправді було зроблено вісім ви
мірів, з яких чотири є необхідними, а решта — додатко
вими.
Приймемо за незалежні невідомі найімовірніші значення
перевищень між точкою D і точками А, Е, В і С, які позна
чимо через х, у, z і и відповідно. На рисунку ці ходи з неві
домими перевищеннями позначені пунктирними лініями.
Далі складаємо рівняння помилок. Скласти їх — це зна
чить виразити результати безпосередніх вимірів через неза
лежні між собою невідомі х, у, z, и або їх функції. Очевидно,
кількість таких рівнянь дорівнюватиме кількості вимірів. У

нашому прикладі їх вісім. При складанні рівнянь будемо
керуватись правилом, що сума перевищень у зімкненому
нівелірному ході повинна дорівнювати нулю. Отже, позна
чаючи виміряні значення перевищень через 1г з відповід
ними індексами, будемо мати:
де Vi, v2, ... ,v8 — невідомі поки що поправки до виміряних
значень перевищень.
Рівняння помилок (а) являють собою прості лінійні функ
ції. Але вільні члени їх ht (перевищення) є величини великі.
Через те для спрощення дальших обчислень замінимо неві
домі х, у, z, и через наближені їх значення х0, уо, z0, и0 плюс
поправки до них (х), (у), (z) та (и), тобто припустимо, що
За наближені значення невідомих краще взяти їх вимі
ряні значення
Підставивши, (d) в (а), після простих перетворень одер
жимо рівняння помилок в такому остаточному вигляді:
x —hx=vu x-~z-rha = v 5,
y —h.,^v,, z—u + he- v a,
z —hs = vs, x — y—h4 = v4,
u—hi = vi, y —z-\-h& = v8,
(*)
x = x0 -f (x),
У -■ Уо + (у),
z - z 0 + (z),
a -- Ua-v(ti).
(b)
(c)
Тоді рівняння (b) матимуть такий вигляд:
x = /z, Л-(х),
у==Ло + ( у),
z ” h-j -}■ (z).
и = /г,г і- (и),
(У
(x) = vu (x) — (z) + 10 = t’5,
(y)-v 2, (2) — (И) — 14=T>6,
(z)-v a, (x)-(y)—l8 = vlt
(y)-(z)^ t-1 6 = г-з,
(e)
де вільні члени дорівнюватимуть:
/j —• /•)= /j — /(j== Oj
/5 — hy
--
Л3 + /tg =* + 10 MM J

tr> ■■= Л з - А; -і- //(; і- -14
/7 -/г, — Л2—/г7>= —18 лш,
/8 - Л2—А3 -І- Л8 -=-|-16 лж.
(О
Кожному рівнянню помилок буде відповідати своя вага,
за яку прийматимемо величину, обернено пропорціональну
довжині 'відповідного нівелірного ходу (див. задачу 2,
§38), а саме
100 км ,гг
Рі ~-Di KM -. і (55,1)
Отже, вагу р 1 матиме нівелірний хід довжиною в
100 км.
Розв'язування рівнянь помилок (е) проводимо при умові
[pvv] = minimum. Для цього складаємо нормальні рівняння,
з яких і знаходимо найімовірніші поправки (х), (у), (z) і (и)
до наближених значень невідомих.
Коефіцієнти нормальних рівнянь обчислюємо за допомо
гою таких двох схем, які для зручності обчислень доцільно
розташовувати поруч (табл. 35 і 36).
Таблиця 35
Схема 1
Номери-
рівнянь
а
ь с (1 1 S
1 і-і
0
0 0 0
+1 4,1
2
0
+ 1
0 0
0
. і-І
9,3
3
0 0 + 1
0
,0
+ 1
5,4
4
0
0 0
+ 1
0
+ 1
6,7
5
+ 1
0
■—1
0
+ 10 + 10
4,7
6
0
0
+ 1
—1
-1 4
— 14
8,0
7
+ 1 -1
0
0 —18
- -18
10,8
8
0
+ 1
...
] 0
+ 16 + 16
14,1
£
+ 3 . + 1
0
0
.-6
—2 ч

С хе м а 2
Номери
рівнянь
ра pb рс
pd. рі
ps
1 + 4,1 0 0 0
0 + 4,1
2
0
+ 9,3
0
0 0
+ 9,3
з
0 0
+ 5,4
0
0 + 5,4
4
0 0 0 + 6,7
0 + 6,7
5
+ 4,7 0 —4,7
- 0 + 47,0
-+47,0
6
0 0 + 8,0
- 8 ,0 — 112,0
- 112,0
7
+10,8
-10 ,8
0
0 — 194,4
— 194,4
8
0
+14,1
-14,1
0 + 225,6
+ 225,6
2
+ 19,6
+ 12,6
—5,4 —1,3
— 33,8
— 8,3
В схему 1 виписують коефіцієнти при невідомих поправ
ках і вільні члени рівнянь помилок (е). Ваги р досить обчис
ляти з точністю до одного десяткового знака.
Величини схеми 2 одержують, множачи величини схеми
1 по стовпчиках на. відповідні ваги р. В рядках £ стоять су
ми величин по стовпчиках.
Контроль обчислень у цих двох схемах такий: суми ве
личин по рядках S повинні дорівнювати сумам величин по
стовпчиках s. Зауважимо, що в схему 1 треба уважно і без
помилково виписувати коефіцієнти при невідомих і вільні чле
ни рівнянь помилок та їх знаки. В противному разі задача
по -врівноваженню буде розв’язана невірно, що виявиться
лише наприкінці обчислень. Те ж саме буде і в тому випад
ку, коли невірно будуть складені рівняння помилок або не
вірно визначені їх вільні члени. 4
Коефіцієнти нормальних рівнянь обчислюють, підсумо
вуючи добутки величин стовпчиків схеми 1 на відповідні по
рядках величини стовпчиків схеми 2- (табл. 37).

Таблиця 3
1
ь\
с\
.
......
.
л\
/]
S]
[ра
)
10,8
. .. .
— 4,7 0
- 147,4
143,3
\рь
1
1
(-31,2
- 14,1 0
1 • 420,0
+ 429.3
\рс
І
+ 32,2
j
— 8,0
- 384,6 — 379,2
[рл
■
....
у
-і- 14,7 І - 112,0 4- 118,7
\РІ
4- 9146,8
49146,8
Ірн
4 9172,3
Після розв’язання нормальних рівнянь (табл. 38) обчис
люємо поправки Vi, и2, ..., Vs до виміряних значень переви
щень, підставляючи знайдені невідомі (х), (у), (г) і (и) в рів
няння помилок (е). Далі визначаємо врівноважені переви
щення і остаточні висоти точок. Обчислення проводимо в
такій схемі (табл. 39).
Таблиця 38
Схема Гаусса—Дулітля розп’н«унання нормальних рівнянь
х
(X а
v ■-
у іС
X S. е 2 4 / (х)
/
(у)
/
(3)
1 І [а +19,6
2 І £, —1
З І (х)-1 + 6,2391
4
5
6
7
І 8
9
і 10
І*
/7
[ 6.1
lh
[с
/7
(У)’
- 10,8
+ 0,5510
- 3,5407
+ 34,2
- 5,9508
+ 28,2492
- 1
- 6,4260
4,7
-14,1
+ 0,5903
+ 5,5665
+ 32,2
- 1,1271
' а /
/
/ («)
І
0
-147,4
-143,3
3 0
+ 7,5201
+ 7,3112
1 0
+ 7,5204
0
+ 420,0
+ 429,3
0
— 81,2203
— 78,9610
0
+ 338,7797
+•350,3390
0
— 11,9925
- - 12,4017
0
— 11,9925
- 8,0
-384,6 .
-379,2
0
- 35,3459
- 34,3626
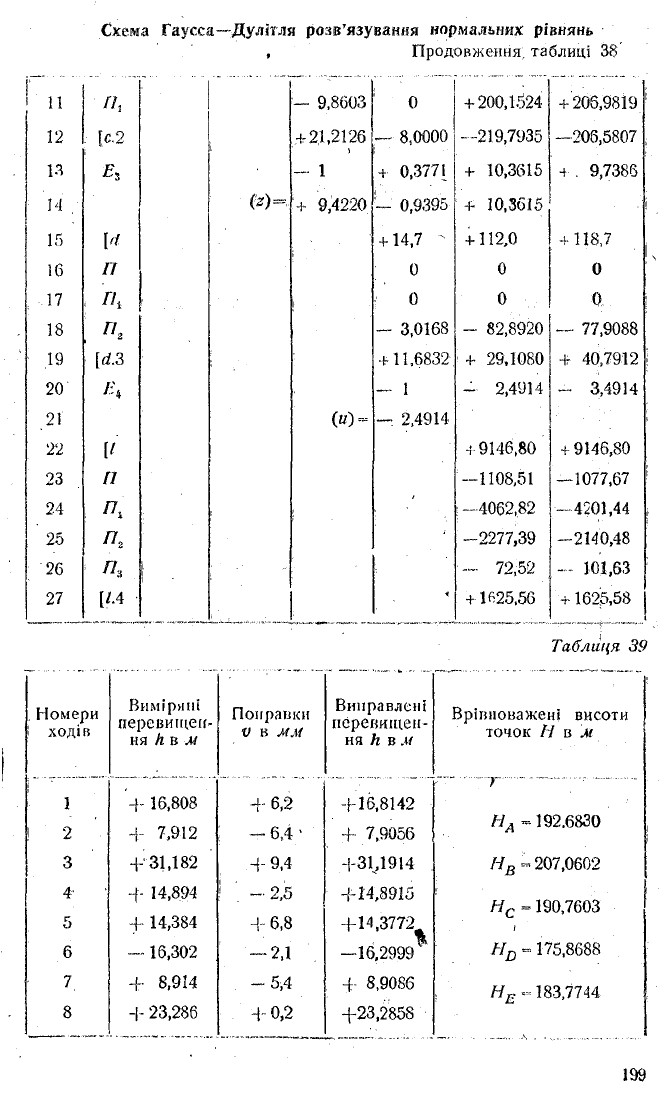
Схема Гаусса—Дулітля розв’язування нормальних рівнянь
, Продовження, таблиці 38
п,
— 9,8603
0 + 200,1524
+ 206,9819
12
; [С-2
+ 21,2126
— 8,0000 —219,7935
—206,5807
13 — 1
+ 0,3771 + 10,3615
+ . 9,7386
14 .
(z)=,
+ 9,4220
— 0,9395
+ 10,3615
15
I«f
+ 14,7 "
+ 112,0 + 118,7
16
ТІ
0
0
0
17
п, 0
о
0
18
, /7‘
- 3,0168 - 82,8920
— 77,9088
19 [йГ.З
+ 11,6832
+ 29,1080 + 40,7912
20
/:4 — 1
- 2,4914
- 3,4914
21
(« )-
—. 2,4914
22
[/
+ 9146,80 + 9146,80
23 П -1108,51
—1077,67
24
".
--4062,82 —4201,44
25
Пг
-2277,39
—2140,48
26 П,
- 72,52
~ 101,63
27 [1.4
+ 1625,56
+1625,58
Таблиця 39
Номери
ході в
Виміряні
перевищен
ня h в м
Поправки
V в мм
Виправлені
перевищен
ня /г в м
Врівноважені висоти
точок Н а м
1
2
+16,808
+ 7.912
+ 6,2
- 6,4 '
+ 16,8142
+ 7,9056
НА -192.6830
3 4-31,182
-1- 9,4
+31,1914 Нв - 207,0602
4-
5
-і- 14,894
+ 14,384
- 2 ,5
+ 6,8
+ 14,8915
+14,3772
—16,2999
Я с = 190,7603
6
— 16,302
— 2,1
HD -175,8688
7,
+■ 8,914 - 5,4 -і- 8,9086
НЕ -183,7744
8 -1- 23,286
+ 0,2
+23,2858

При обчисленні врівноважених перевищень необхідно вра
ховувати, ті їх знаки, з якими вони уходять у рівняння по
милок (а). Наприклад, для сьомого і восьмого перевищень
будемо мати:
х - у = + /г7 + г>7,
у - 2 - _ А 8 + ® 8.
Отже, до першого з них поправка v7 алгебраїчно додаєть
ся, а від другого віднімається.
Для оцінки точності обчислюємо безпосередньо вдруге
для .контролю [pvv] (табл. 40).
Таблиця 40
1 v
Р
pv
pvv
1
+ 6.2
4,1
+25,42
157,604
2
-6 ,4 9,3
-59,52
380,928
3
|-9,4
6,4 1-50,76
477,144
4
-2 ,5
6,7
-16,75
41,875
5
4-6,8
4,7
+31,96 217,328
6
-2,1 8,0
— 16,80
35,980
7 -5,4 10,8
-58,32
314,928
8 1 0,2
И,1
1- ?.82
0,564
[pvv] - 1625,651
В межах точності обчислень знайдене тут [pvv] повинно
дорівнювати тій же сумі, одержаній в схемі Гаусса—Дулітля!
Середню квадратичну помилку, яка відповідає одиниці вг^
ги, обчислюємо за формулою (51,29):
і і Г [pvv] . -і Г І625Д55Ї ол о
± у п.. ь “ ± у 4 —20,2 мм.
Раніш ми зазначали, що вагу р = 1 матиме нівелірний хід
довжиною D -— 100 км. Отже, середня квадратична помилка,
яка припадає «а 1 км нівелірного ходу, буде дорівнювати:
■ і 20,2 п
І ~7—= = І ~~7=— ~ 2,0 мм.
- у о /100

§ 56. ВИЗНАЧЕННЯ ВАГИ ФУНКЦІЇ
ВРІВНОВАЖЕНИХ ВЕЛИЧИН ПРИ ВРІВНОВАЖЕННІ
ПОСЕРЕДНІХ ВИМІРІВ
Величини, які одержують в результаті врівноваження
способом врівноваження посередніх вимірів, можуть служи
ти для визначення нових величин. Очевидно, ці останні будуть
функціями врівноважених величин х, у, z, .. ., и. Через те,
що ці аргументи одержують з деякими помилками, то і об
числені за ними функції теж матимуть помилки. Отже, в
зв’язку з цим виникає задача оцінки точності функцій врів
новажених величин.
Цю задачу ми можемо розв’язувати, якщо нам будуть ві
домі: вага Pf даної функції F (х, у, z, ..., и), яку назива
ють ваговою, і середня квадратична помилка ц, що відпові
дає одиниці ваги. Тоді середню квадратичну помилку т,
функції знайдемо за відомою уже формулою
тр~ ± ут;У <56>1)
де величина \і, у свою чергу, визначається за форму
лою (51,29).
Таким чином, для оцінки точності функції врівноважених
величин необхідно визначити її вагу.
Розв’яжемо цю задачу в загальному виді. Нехай маємо
функцію врівноважених величин
F(x, у, z,..., и). (56,2)
Тому що ця функція може бути складною, приведемо її
спочатку до простого лінійного виду. Для цього аргументи
напишемо у вигляді:
х ~ х 0 + {х),
У~Уо + (У),
z — z0 + (2), (56,3)
и = и0 + (и),
де Хо, уо, z0, .... и0 — наближені значення аргументів, (х),
(у ), (z), (и) — поправки до них, які знаходимо, розв’я
зуючи нормальні рівняння.
Підставимо ці значення аргументів у функцію (56,2) і
розкладемо її в ряд Тейлора:
/7{х0 + (х),у0 + (у),2г0 + (2;),!. и0 + (u)} = F (х0, уо, 2:0
-----
,и0)-\

При розкладанні можемо обмежитися членами з поправ
ками в перших степенях, тому що (х), (у), (Z), (и) —
величини малі.
Введемо такі скорочені позначення:
F(x, у, z, ..., и) — F, F(x0, у0,г0,..., иа) = F0,
( £ ) г л - ( * ) , - ' » ( *
.......
( я ) , - л « а д
де k — кількість аргументів. Ці часткові похідні , fh
вагової функції називаються ваговими коефіцієн
тами. Обчислюються вони за наближеними значеннями ар
гументів х0, уо, . . . , и0. Тоді функцію (56,4) можна за
писати так:
f = F0+f1(x)+f3(y)+f3(z) + . . -+fk(u). (56,6)
З теорії помилок нам відомі такі загальні формули для
визначення оберненої величини ваги функції незалежно ви
міряних величин:
<5 6 - 8 >
якщо виміри аргументів рівноточні.
Але ці формули для нашої задачі використати не можна,
тому що вони справедливі лише для визначення ваг функ
цій незалежних величин. Аргументи же
(х), (у), (z), . . (и)
функції (56,6) — залежні між собою, тому що їх знаходять
при умові [vv] = minimum або [pvv] = minimum.
В зв’язку з цим виключимо (х), (у), (г), ..., (и) з функ
ції (56,6), замінивши їх величинами /і, h, .... U, які незалеж
ні між собою. Це можна зробити за допомогою так званих
неозначених множників у такий спосіб.
Додамо до функції (56,6) нормальні рівняння, помноживши
їх спочатку на неозначені поки що множники qi, q2, . . ., <7* :
F = F0 +fi(x) + /2(y) + /3(z) +... +Mu) +
+ §aa](x) + [ab](y) + [ac](z) + .. , + [аЩи) + [аЩд\ +
-Г{[а&](л-) 4- [bb](y) + j bc](z) +... + [bt](u) + [bl\}q2 +
+ {[a*](x) + [fc*]0 /) + [c<](z)-|-.. . + [tt](u) + [trbqk,
