Бугай П.Т. Теорія помилок і спосіб найменших квадратів

Подождите немного. Документ загружается.

середньої квадратичної помилки т ми можемо ьикористати

лише найімовірніші поправки до результатів безпосередніх

вимірів. Це можна зробити завдяки тому, що між істинними

помилками Ац Л2, ..., Д„ і найімовірнішими поправками иі,

V2, .. ., vn існує певний зв’язок.

Щоб встановити цей зв’язок, візьмемо систему рівнянь по

милок в їх лінійному виді:

ахх + ЬіУ+ ... + t^i -і- /, = г\ ,

а2хл- Ь2у + ... + Uu -f /3 = v2,

■ ~

.............

..............

(51,1)

С*:;Х . Ь „ у . . . : ( ц і ї ' I n " 't'.’h

де

U -ft (*<>< Уо,---, »o)—Li. (51,2)

Замінимо в рівняннях (51,1) найімовірніші значення неві-

’ домих х, у, . .., и, які знаходимо за способом найменших

квадратів, їх істинними значеннями X, Y,.. ., U. Тоді в пра

вих частинах рівнянь помилок найімовірніші поправки v-L за

міняться істинними 'поправками. Позначимо їх через Sj, s2,....

e„. Очевидно, що є/ щодо своєї абсолютної величини до

рівнюють істинним помилкам А і і відрізняються від них ли

ше знаком, т о б т о —£і =А; .Отже, ми можемо записати таку

систему рівнянь:

b^\-і- . . . + tJJ-V = Sj,

CLoX "Ь Ьъ Y "Ь tt(-J“1^2“

/ ____Г

....................

..............

(51,3)

апХ -і-bnY + . .. -і tnU-£ln*= ?„•

Віднімаючи тепер від обох частин рівнянь (51,1) відпо

відні їм частини рівнянь (51,3), будемо мати:

' al(x-X )\-bl(y—Y)-r...-\-tl(u—U)=vl—£l,

a2(x-X)-\-b2(y — Y)+ ... \-t2(u—U) = vz~-t2,

an(x—X) + b„(y — Y) + . ■. + t„(n —U) = vn -s„,

:ів ід к н , вводячи для скорочення записів позначення

х — Л' = 5л-,

у —Г-оу,

•

...............

(51,4)

U—U — OU,

одержимо:

afix-V blЗу + .. . +£18й + г1 = vu

CL-i<iX 4- V • - • 4" 4-

(51,5)

a„ox-\-bnZy . . . \-tnou-i-zn = vn-

Таким чином, замість системи рівнянь помилок (51,1) ми

одержали еквівалентну їй систему рівнянь (51,5), яка від

різняється від системи (51,1) лише тим, що в ній замість

невідомих х, у, . . и стоять їх істинні помилки 8х, 5_у,..., 8и, а

замість вільних членів /ь /2, .. ., /« — істинні поправки

г,, результатів безпосередніх вимірів.

У попередньому параграфі були встановлені різні види

залежності між .найімовірнішими поправками vx, v2, . . ., v„, з

одного боку, і коефіцієнтами та вільними членами рівнянь

помилок (51,1), з другого боку. Ці залежності виражаються

формулами (50,1), (50,3), (50,7). Через те, що рівняння

(51,5) мають усі властивості рівнянь помилок, то згадані ви

ще залежності будуть справедливими і для них. Отже,' ми

можемо написати рівняння

[vv[ = [є-и]... |es.&], (51,6)

де к — кількість невідомих, і

1^ 1 . ї й . і)!' гі7 )

1 1 1 1 [аа\ [66.і| [//.(А- — 1)] •

Всі члени в рівнянні (51,7) додатні. Тому, беручи до

уваги, що $і = — Дйого можна записати так:

1 > 1 1 ійя] [66.1] \tt.(k -1)] '

Формула (51,8) і виражає зв’язок між найімовірнішими

поправками vt та істинними помилками Д,- до результатів ви- 1

мірів. З неї видно, що завжди

[г«гг]<[ЛД]. (51,9)

При досить великій кількості п виміряних функцій

h (х, у,..., и) в порівнянні з кількістю k невідомих х, у,... ,и

найімовірніші значення останніх будуть дуже, мало відріз

нятися від їх істинних значень X, Y, ..., U, а через те й

[ДД] мало відрізнятиметься від [vv]. Отже, в цьому випадку

всі останні члени в правій частині формули (51,8) в порів-

нянні з першим членом [ДА] — величини малі і їх граничні

значення при п ->оо дорівнюють нулю, тобто

Ііш

....

/І -> 00

\аа\

.. [6Д.1]2 ,,

!,пп; iw.,1! (,> (біло)

Для виведення формули, за якою повинна обчислятися

середня квадратична помилка т безпосереднього виміру, ско

ристуємося залежністю (51,8). Але спочатку візьмемо до

уваги таке.

При обчисленні вільних членів рівнянь помилок /г- за фор

мулою (51,2)-ми використовуємо остаточні значення L\, L?.

. . Ln вимірів функцій fi(x, у

..........

и), кожне з яких при

рівноточних вимірах може бути середнім арифметичним з

результатів багатьох повторних вимірів цих функцій. Так,

наприклад, остаточні виміряні значення кутів на станції, які

ми в §44 врівноважували за способом врівноваження посе

редніх вимірів, можливо, були одержані як середні арифме

тичні з результатів багатьох повторних рівноточних вимірів.

У зв’язку з цим можна вважати, що взагалі функції

/1, [г, ■ ■ ■, fn були виміряні кожна s разів при однакових

умовах, а значить і з однаковою мірою точності.

Кожному з цих s рядів вимірів відповідатимуть свої систе

ми істинних помилок

Д(;>, Л» (51,11)

і найімовірніших поправок

Ї-Т, г.(9, . .. , v"'. (51,12)

де і 1, 2, . . . , s, і для кожного з них можна написати рів

няння виду (51,8):

Г-,'г1«[Л'3І_ (аД']! [Й4'ЛІ2 іа'.(й-П)3

1 ! 1 [аа] " [ЬЬЛ] [tt,(k— 1)] ’

ШП .. І Л»21 _ И Т 16АТ _ _1**Ч*=})Г /г, 104

' 1 [аа] [ЬЬЛ] [tt.(k 1)1 ’ (51,13)

Іг,Мд(,)1 _ і2 _ _ Г

^ 1 ~ 1 1 [аа] [ЬЬЛ] • • • [tt.ik—lj] •

Якщо кількість s рядів вимірів буде досить великою, TQ,

беручи до уваги (51,10), замість рівнянь (51,13) можна взя

ти середнє арифметичне з них. Позначаючи середні значеная

відповідних величин рискою зверху, одержимо:

Г^1_ЇД2Т _ Ї « Д І _ І ^ _ A ^itzlK (51,14)

> I J [aa\ \bb. 1] ••• 1)] ' .

Знайдемо tenep, чому дорівнюють середні значення вели

чин у правій частині рівняння (51,14):

|Д2] _ ? [^ J _ [V ^l + ІД/ у81 + _ + \^С‘Г\

(і= 1, 2, ... , s).

Ллє при досить великому s можна припустити, що

1Аб т- (/« 1, 2, . . ., п), (51,15)

звідки

Далі для кожного з s рядів вимірів маємо

|яД^ ] 2 = (а, А/Ол-аЛ/»-)- ... та„Д/ ,;)2

а,2Д/1'’" і- -і- . . . 4 а„'! 1,/і>2 4

42 (а, а, V у V у + а і и* Д /°Л/ У + • ■ • +-а„_ і «» д» V у V і').

Середнє арифметичне ч них дорівнюватиме:

|аД| =*а, —-

-----

ьа->— --- 4 . - .+ а я s~~-r (5^ 57)

гд СУдГУ ] [д,^д/у] , , о Ід(У«-і дяҐУ1

4-2а, а ,—

------

3142а, а3‘- - J4 •.. 4 2ап- 1ап

------

S 1 * S S

Але згідно з четвертою властивістю випадкових помилок

lim

s-coo

іУ " У 5 „ о (j, 1і--=\,2

-----

П] ]фК), (51,18)

л тому при конечному, але досить великому‘S у формулі

(51,17) подвійними добутками можна нехтувати. Отже, взяв

ши до уваги (51,15), будемо мати:

[а Д]- = а ,2 /и- 4 а*г т1 - ... 4 а„2т2,

або

(а.Д|2= |аа| tv?. (51,19)

Так само можна встановити й такі рівності:

\b А]2 *= \ bb] т2,

\с А]2 = [сс\ /ге2,

............................. (51,20)

[ZА]2 = \tt\ /ге2.

Знайдемо тепер середнє значення [&Д.1]2. Для цього за

пишемо таку очевидну рівність:

[МГУД]2= ( [ & А « ] - № р ) 2,

або

\ЬЬ<0.\у- = [6AW]3 + g;[aA r/)]2_2g[aA № ] [ЙДГО]. (51,21)

Враховуючи (51,19) і (51,20), середнє значення з рів -

ностей (51,21)

{ЬАЛ]^\ЬЬ)т2 + [^ \ а а ) т2-2 [“Д\аА][ЬЦг (51,22)

Але

[а У> І \ЬА(Ц = [аЬ\ [Д«2] + [сц bh при j Фіг,

а тому, беручи до уваги (51,15) і (51,18), середнє, з цих рів-

Н0С.ТЄЙ

|аД] [b А] = [ab] пі1. (51,23)

Підставивши (51,23) в (51,22), знаходимо:

\ЬА-\}'l = [bb\ пг+ [^ ]г\аа\ т * -2^[аЬ j то2,

або

[й A - І]2 -[ЬЬ-\]т2. (51,24)

Так само можна довести і такі рівності:

[сА-2\-=[сс-2\ т\

1.1.11 1.11

............

(51,25)

[*Д-(й-1)]- = [« •(£ -1)]/ге2.

Нарешті, підставимо знайдені середні значення (51,16),

(51,19), (51,24) і (51,25) в (51,14):

[■»’[ = пт--~т2—т-—... т2 = m2(n—k),

k разів

звідки

(51,26)

де k — кількість невідомих.

При достатній кількості рядів вимірів s величину [и2]

можна замінити сумою [t>u] кзадратів найімовірніших попра

вок до результатів І,, L2, Ln безпосередніх вимірів. Тоді

В цій формулі величина п—k дорівнює кількості додат

кових вимірів. Чим більше буде проведено додаткових ви

мірів, тим з більшою точністю буде знайдена за формулою

(51,27) середня квадратична помилка одного виміру.

Якщо кількість невідомих k = 1, то

При врівноваженні нерівноточних посередніх вимірів

оцінку точності проводять за допомогою середньої квадра

тичної помилки одиниці ваги за формулою

Як відомо з попереднього викладу, розв’язування нормаль

них рівнянь методом послідовного виключення невідомих зво

диться до заміни цих рівнянь системою еквівалентних рівнянь

і до одержання елімінаційних рівнянь, які необхідні, по-

перше, для утворення величин рядків добутків Я£ і, по-друге,

для обчислення самих невідомих. Запишемо згадані систе

ми рівнянь для випадку п’яти невідомих у вигляді схеми

(табл. 25), яку будемо називати компактною схемою розв’я

зування нормальних рівнянь. У цій схемі таблиці коефіцієнтів

нормальних, еквівалентних та елімінаційних рівнянь для ско

рочення позначимо відповідно через А, В, С.

(51,27)

(51,28)

(51,29)

§ 52. КОМПАКТНА СХЕМА РОЗВ'ЯЗУВАННЯ

НОРМАЛЬНИХ РІВНЯНЬ

Таблиця 25

Компактна схема розв’язування нормальних рівнянь в позначеннях Гаусса

' к

2 ж

1 2

4 5.

о S

с °-

ь]

с]

е]

Таблиця А

[а

[яа]

[ab 1 [ас]

\ad\ [ ae\

[я/]

[as]

[Ь

[be]

[,bd] [be

[«]

№

1с

]СС]

[erf] [cel

[cl]

[csj

• И

\dd\

[de]

[dl]

\ds\

-5

Іе

[ее]

[el] [es]

[U]

[/s]

Таблиця В

1 [a

[ae]'

[ab] |ac]

[ad[

[ae 1

\al\

[as]

[6.1 [bb. 1]

[6c.l] [bd. t]

[be. 1]

1W.1I

[bs.l]

3 [c.2

[cc.2]

[erf 2]

[«■•21

[c/,2]

\cs.2]

[rf.3

[rfrf.3]

[rfc.3|

[rf/.3|

[rfs.3]

[eA

[ee.4| [elA]

[<?S.4]

[/.5

............\

[//.51

I/S.5)

Таблиця С

—і

_ И ] .

і««ї.

[aa]

Jad]

[да]

І"«Г

_И ).

\aa) \

—1

|&c.l]

[66.1]

[fed. 1]

[Ш ]

[he. 1]

[66.1]

[6/.1]

[66.1]

[bs.l]

[66.1]

'Ey

- 1

[cd.2]

[cc.2]

[ce.2]

[cc.2]

[c/.2]

[cc.2]

[cs.2]

[cc.2]

Ец

—1

[de.3]

Jrfrf.3]

[ШЯ]

[rfd.3]

[rfs.3]

[rfrf.3]

— 1

[elA]

[eeA[

[es.4]

[ее.4]

хг

* | j

Кожен з коефіцієнтів еквівалентних рівнянь можна за

писати в розгорнутому виді, наприклад, коефіцієнт [de.‘3>\ до

рівнюватиме:

[de.Z]~[de]~

([<*)

(П)

(52,1)

Отже, для переходу від нормальних рівнянь до еквіва

лентних необхідно кожен коефіцієнт останніх рівнянь запи

сати в розгорнутому виді і обчислити всі необхідні величи

ни рядків добутків ГІ. Для проведення всіх цих операцій і

розроблена схема Гаусса—Дулітля.

Але необхідно зауважити, що величини рядків добутків

If при обчисленні коефіцієнтів еквівалентних рівнянь є допо

міжними і фіксування в схемі їх числових значень не є обо

в'язковим. У зв’язку з цим при розв’язуванні нормальних

рівнянь можна не розкривати символічні дозначещія коефі

цієнтів еквівалентних рівнянь, а безпосередньо обчисляти і

записувати їх числові значення, опускаючи записування ве

личин рядків добутків П. Основана на цій ідеї схема розв’я

зування нормальних рівнянь називається компактною.

Обчислення в компактній схемі проводяться в такій послі

довності:

1. Обчислюють і записують в схему коефіцієнти і вільні

члени нормальних рівнянь і контрольні суми (таблиця А),

2. Виписують в таблицю В коефіцієнти першого еквіваа

лентного рівняння, які дорівнюють коефіцієнтам першого

нормального рівняння.

3. Обчислюють коефіцієнти першого елімінаційного рів

няння Еі (таблиця С).

4. Обчислюють послідовно коефіцієнти [ЬЬ. 1], [ЬсЛ\, ...

другого еквівалентного рівняння.

5. Обчислюють коефіцієнти другого елімінаційного рів

няння £ 2 і т. д. і, нарешті, обчислюють значення невідо

мих Хі, Х% . . . ■

Контроль обчислень коефіцієнтів еквівалентних та елі

мінаційних рівнянь такий самий, як і в схемі Гаусса—Ду

літля.

Правило для обчислення величин елімінаційних рядків

Еі, Е2, ... досить просте, а саме: коефіцієнти елімінаційних

рівнянь дорівнюють відповідним коефіцієнтам еквівалентних

рівнянь, поділеним на квадратичний коефіцієнт з оберненим

знаком.

Виведемо тепер правило для обчислення коефіцієнтів дру

гого, третього і т. д. еквівалентних рівнянь. Для цього проана

лізуємо структуру формули (52,1).

Коефіцієнт [de.3] стоїть в таблиці В у 4-му рядку і 5-му

стовпчику. На тому самому місці в таблиці А стоїть і коефі

цієнт [de\ правої частини формули (52,1). До нього ще треба

додати добутки П, Пі, П2. Кожен з них складається з двох

множників: перші стоять в 4-му стовпчику таблиці С, другі - -

в 5-му стовпчику таблиці В. При описаному вище порядку

обчислень усі ці множники при обчисленні коефіцієнта [de.3]

уже відомі. Отже, безпосереднє його обчислення проводиться

за таким правилом: коефіцієнт [de.3], який стоїть в 4-му

рядку і в 5-му стовпчику таблиці В, дорівнює відповідному

коефіцієнту таблиці А плюс сума добутків коефіцієнтів 4-го

стовпчика таблиці С на відповідні по рядках .коефіцієнти 5-го

стовпчика таблиці В.

Легко переконатися, що за таким правилом можна об

числяти й інші коефіцієнти еквівалентних рівнянь. Це пра

вило в загальному виді можна сформулювати так: коефі

цієнт, який стоїть в t-му рядку і в /-му стовпчику таблиці В,

дорівнює відповідному коефіцієнту таблиці А плюс сума до

бутків раніш обчислених коефіцієнтів ї-го стовпчика таблиці

С на відповідні по рядках коефіцієнти /-го стовпчика таб

лиці В.

Таким чином, ми бачимо, що основна ірізниця між схема

ми Гаусса—Дулітля та компактною полягає в тому, що в

першій з них обчислюються і записуються всі величини ряд

ків добутків П та проводиться контроль їх обчислення по

кожному рядку окремо, тоді як в компактній схемі запис і

контроль усіх- рядків добутків пропускаються. При утворенні

ж коефіцієнтів еквівалентних рівнянь добутки хоч і обчис

люються, але їх можна зразу підсумовувати на арифмомет

рі або лічильній машині і результат безпосередньо додавати

до відповідного коефіцієнта нормальних рівнянь.

Звідси випливають такі очевидні переваги компактної

схеми розв’язування нормальних рівнянь перед схемою Гаус

са—Дулітля.

1. Таблиця .коефіцієнтів і вільних членів нормальних рів

нянь входить до складу самої схеми, а тому немає потреби

ці величини виписувати з окремої таблиці коефіцієнтів нор

мальних рівнянь, як це має місце при розв'язуванні рівнянь

в схемі Гаусса—Дулітля. «■„.

2. Запис і контроль обчислення всіх величин рядків до

бутків не проводиться, що значно зменшує кількість запи

сів, затраченої праці та розміри схеми.

3. Обчислення коефіцієнтів і вільних членів еквівалент

них рівнянь проводиться шляхом нагромадження на арифмо-

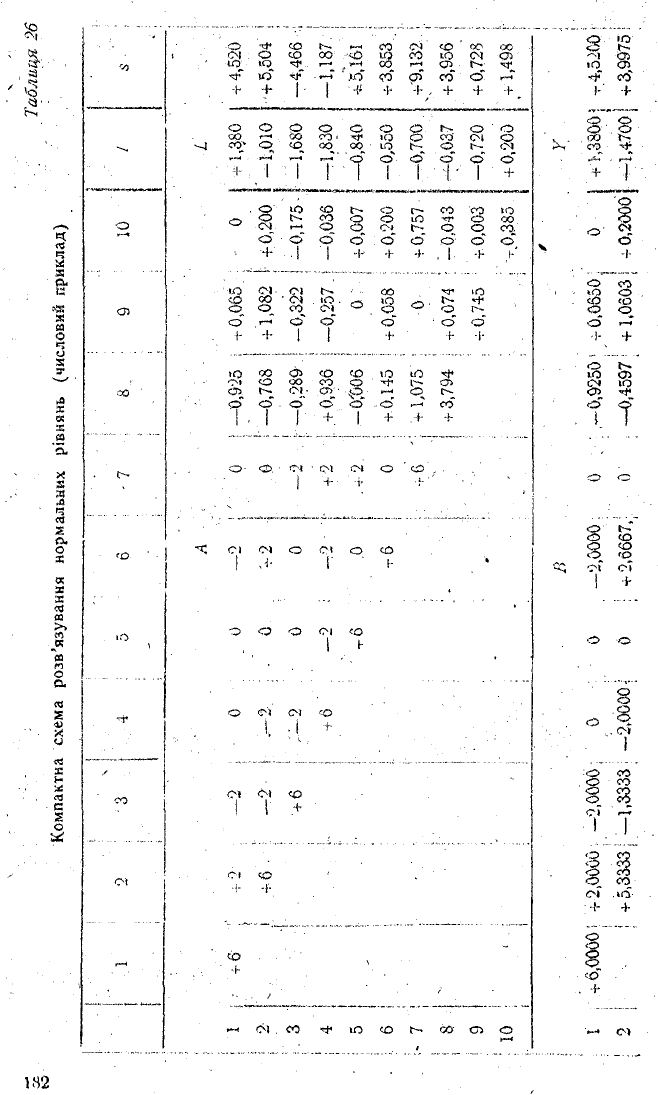
Компактна схема розв’язування нормальних рівнянь (числовий приклад)

йг: ■

, з

'о

ь!”

гл

‘ ,

■О "'**

гм . О

ю IQ

•ф" ІО

—4,466

со

оо

со

‘I’

сО

С>

СО

СП

со

ОО

г-

о"

C7J

о о

О о

о о

ОО

Г-*

CO I

«о

со'

о \

СО' О tq

00 •

о г-

<м

г-Г

r-i*

rr-Г

'о

о4 о o ’

о"

+ 1

: І

■ 1

' 1. ■'

---

----

-------

<о

Г'- CD г- со

со to

t--

СО

о 00

О ^ CM

•—*

О-»

г-

о о

СО.

о • о

о*

<о

О'

о*1 о

, I

-1-

ю <м

гг

О GO

• C-i

«о

■

1"-

<Уі

О CD

со сч

f- -1-

о"

; о

-І-

»0

Ф <о

СО

ю ю

о» о

со

•rf

00 '

оэ «М- а>

■,р ■

г—

о о • o'

о*

»-«

СО

! . 1

-f-

-Ь

О-

о- о.

гм <м

о ’ о

Н- •f-

. '

___

*о

'Х,

Cl сч

! J-

о С»

сО

і О

О О

<о

‘ ,

<©

• і

-f-

—

-------

со

О* <N

і i

<о

1 1

ч-

—

Сч o

і- -}•

...............

—

-h

,•

СО

ю <о

►—*

---

•.

---

------

...

.........

- -

.. Л

........

.....

+6,0000І -г2,0000: -2,0000 ; 0 0 -2,0000; 0 — 0,9250' *0,0650 ] 0 >1,3800j ^ 4,5200ї

і +5,3333! — 1,3333: -2,0 0 0 0 і о ! +2,6667,’ 0 , —0,4597 ' + 1,0603і + 0,2000 — 1,4700 j +3,9975!

■ і . . : . і . . і . і