Бугай П.Т. Теорія помилок і спосіб найменших квадратів

+ 5,0000 '.—2,5000 O' 0 - 2,0000 і —0,7122 ; —0,0353 ; —0,1250 -1,5875 j -1,9601 j

- 4,0000 -2 ,000 0 : -1 ,0 0 0 0 . -1,0000 ’ -Г0,4075'; -г0,1230: -0,0235 —3,17501 —0,6630 :

• ✓ ‘ 1

+ 5,0000; --0,5000 . -r 2,5000 - 0,1978; +0,0615: -0.C048 -2,4275 I +4,8270

. . ! ■ ' ! ' і

; +3,7000; -0,5000 + 0,1882; —0,4136; +0,09364 —0,3915 3 +3,6764:

. . ’ j " T 3,63-24: +0,5639: —0,0197' +0,7026 * 0,7254 j +5,6048

co“ o o'

•!* -b +

о

<м

ю

о

■ф

а>

ю «о

Г-4

со о

о"

ол

1

о

'1*

оО

со

V}*

ч*

оо

»о

01

г—4

о

CS

О о"

о

1

‘Ь

ю 00

05 <М

h-

*

о‘

-1-

о '

-ь

co

i-

>

Ґ

■cO -F Ю <C f-* ' ОО О О

СО

з

о

<N

05

сО

о"

'}*

о

+

<о

О)

о

СО

ю

0> О СО

*-* r-v, <м

Ю I"’ со

О

~ о” Г~‘

I I ]

. . 0О-

N (м. c-і

со

о* о ” о

I »- 'І*

00

ю

00 1^-

со

ю ю

со

ю

05

о

оо о о>

—м

О)

со

I"» *т

Т-Н

ол

г-

01

о"

о о

о"

O'

o '

о

Сі

. 2

о

ю

о 05

о со

о

Ої

г-.

*о

ю

ю со СО о

СО

сч

OI о

•ф 00

о

о о

о~

о“ о~ о~

о

o’*

■ о '

о

1

-1' -f-

1

f-

1-

со

,

00 со 00

оо

о см

ю со

о>

о

со

о ю

о о

о

►—

о

1

о

о“ ож

о

o '

о"

о” 1

1

I

І.

•г

-ь

і

----

__

04

'•О

00

о

О

ч*

о

н*

05 со

г-4 О

О СО

О

§

1

ю

Ю

«о

о

с»

СО

со

г-.

o '

-к

со

о>

о

o '

I

о

т**

о4

о

VO

«м

о

S3

о" .I

со

о>

O'}

СО О

со о

со «о

О о” о*

Ь І

1.0

ОІ

о\

О

о

+

о

ю

о

S

со ю

о

•ь

о

I-

ю

о>

<•-*

£2 Q

Я 8

со С

1

о" о‘

І- -I-

О)

00

о

ч-

я

со

о

ч -

со

о

Ю (£5 N УО 05

метрі добутків без їх заокруглення, тоді як в схемі Гаусса—

Дулітля кожний добуток (величини рядків добутків П) за

округлюється окремо, що приводить до зниження точності

обчислень за рахунок нагромадження помилок заокруглень.

4. Всі величини, які входять у компактну ^хему, розта

шовані настільки компактно і зручно, що обчислення про

водяться досить просто і легко без зайвого напруження ува

ги обчислювача.

До недоліків компактної схеми треба віднести меншу

кількість проміжних контролів обчислень, ніж в схемі Гаус

са—Дулітля, де існують контролі обчислень величин рядків

добутків. Але досвідчений обчислювач може обійтись і без

них.

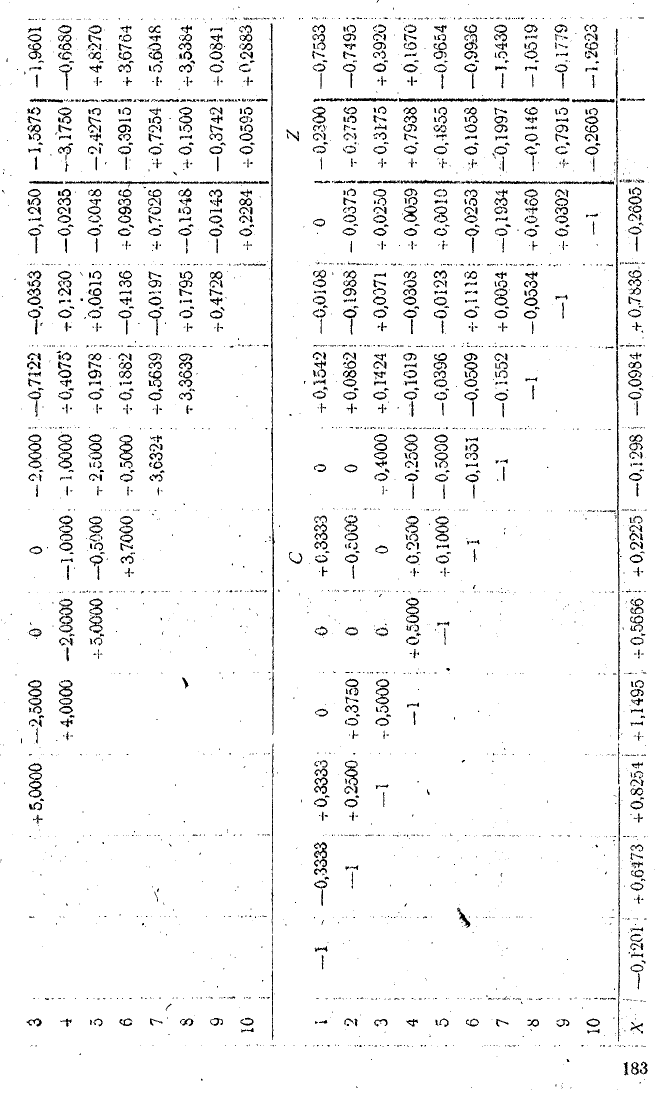
Для прикладу подаємо компактну схему розв’язування

нормальних рівнянь у числовому виді для 10 невідомих

(табл. 26).

§ 53. РОЗВ’ЯЗУВАННЯ НОРМАЛЬНИХ РІВНЯНЬ

МЕТОДОМ ПОСЛІДОВНИХ НАБЛИЖЕНЬ

Усі числові методи розв’язування нормальних рівнянь

можна поділити на дві основні групи: точних та ітеративних

методів, або методів послідовних наближень. Під точними

методами розуміють ті, які дають розв’язання рівнянь за

допомогою конечного числа елементарних арифметичних дій.

Кількість необхідних для цього обчислювальних операцій

залежить в основному від виду схеми для обчислень та від

кількості невідомих. Неточність знайдених при розв’язуванні

задачі невідомих залежить лише від заокруглень числових

величин, які неминуче доводиться робити при обчисленнях.

Основним класичним методом цієї групи є метод, осно

ваний на ідеї послідовного виключення невідомих. Для нього

Гаусс розробив алгоритм1, в результаті застосування якого

задана система рівнянь перетворюється в еквівалентну їй

систему, з якої вже легко знаходяться значення невідомих.

Для проведення обчислень за цим методом ми детально роз

глянули дві схеми: Гаусса—Дулітля і компактну.

Ітеративними методами (від латинського слова iteratio.

що значить повторення) розв’язування рівнянь називаються

такі, які дають можливість шляхом багаторазового застосу

вання певної математичної операції одержувати спочатку

наближені, а далі все більш і більш точні значення невідо

мих. Остаточне розв'язання задачі одержують як границю

послідовних наближених значень відшукуваних невідомих.

і Алгоритм — слово арабське, яке означає сукупність математич

них дій для рішення даної задачі, наприклад алгоритм виключення неві

домих, алгоритм добування кореня з числа і т. д.

m

Збіжність процесу послідовних наближень залежить голов

ним чином від коефіцієнтів рівнянь. Наприклад, існують такі

системи рівнянь, для яких 'процес послідовних наближень

сходиться дуже повільно, а іноді навіть розходиться. Але

в окремих випадках збіжність настає досить швидко. Це бу

ває, наприклад, тоді, коли в системі нормальних рівнянь

діагональні або квадратичні коефіцієнти значно більші від

неквадратичних. А такі системи рівнянь часто доводиться

розв’язувати в геодезичній і астрономічній практиці.

Основні переваги ітеративних методів розв’язування ліній

них рівнянь полягають в тому, що 1) всі обчислення прово

дяться за досить простими математичними правилами в про

стих’ схемах, 2) помилки, допущені при обчисленнях, ви

правляються в процесі наступних наближень, а через те від

падає потреба проводити додаткові контрольні обчислення і

3) всі величини при обчисленнях одержують шляхом нагро

мадження на арифмометрі окремих добутків, що значно змен

шує в них помилки від заокруглень.

Завдяки цим особливостям методу послідовних набли

жень застосування його для розв’язання рівнянь може дати

значний ефект, якщо є дані сподіватись швидкої збіжності

процесу ітерації.

Розглянемо найчастіше вживані прості способи розв’язу

вання нормальних рівнянь методом послідовних наближень —

способи Якобі і Зейделя.

Спосіб Якобі. Суть його розглянемо на такому прикладі.

Нехай маємо систему чотирьох нормальних рівнянь, яку до

цільно зобразити в такому явному виді відносно невідомих:

у- _ _ К6] „_■[£?] * _ lad\ п —

Л v [аа]У [аа[ {аа] [аа]'

V - _ Г - [-Ч г _ [¥ \ „ М

Jbb]x ' [bb] [bb]u [bb]’

_

____

[ас] [be] (53,1)

fee] [сс] [сс] [сс]’

„ - г _ М М г -

[<ta] [dd]y [dd[ [ddy

Виходячи з того, що величина вільного члена в кожному

нормальному рівнянні залежить в основному від того неві

домого, при якоіау є найбільший квадратичний коефіцієнт, ми

можемо для одержання значень невідомиз* в першому на

ближенні в нормальних рівняннях відкинути всі члени з

неквадратичними коефіцієнтами при невідомих. Після цього

одержимо:

*■ = __І^І V = _

[аа]’ > ] ’

, _ _ и „ (

[сс]’ 1 [ddy

Значення невідомих у другому наближенні одержуємо,

підставляючи числові значення невідомих у першому набли

женні (53,2) в рівняння (53,1):

.. .. _ И І „ .....[ас\ \ad\ _{al\

2 [аа\-^1 [да] 1 [<;а] ■ 1 [ла|*

№

„їм.. І

Ьсі]

[

ы}

т хї ~ [ьь\ 1 [ьь] 1....[її]' (53,3)

И ] t&c] [cd] [с/]

” [сс] ” [сс] Уі ><■[ иі " [сс] ’

М і _[bd] И ] [ЛІ

\dd] 1 [ddy1 [dd\ 1 \dd\'

І взагалі вл-му наближенні

_ H I v - [дс1 r // [я/1

Л‘ [аа\У і~1 [аа\ 1~х" [аа\ ' л~ [аа\>

\аЬ] [6с] [bd] [&£]

\bb\Xi ! ' ~ m Zi’V' \ЬЬ)ІІІ~Г Ш (53,4)

_ I rtC) V-

_

„ J Cd\-t, - tC/l

' [cc\ 14 [сс]Уі~л

’

fee]

U ,~r

[сс] ’

[ad] [bd] Jdl\

\dd\ ' 1 {dd]yc~x [dd]"1 ' [rfrfj-

Замість того, щоб відшукувати значення невідомих в кож

ному наближенні, краще обчисляти поправки до значень-неві

домих у першому наближенні Х\, у і, Zi, U\ за формулами, які

виводяться так. Введемо для поправок позначення

X [ JC 2 А і j

8У і —Уз --- У і.

bzl = z2-~z1, (53,5)

5гі, = їй — u lt

і взагалі

<>Ч ^

ОХ і ^ JCi-\-\ X it

ЪУ1=УМ”УГ,

oZi^Zm—Zi, (53,(3)

but = Ui (.і — iii-

Щоб одержати числові значення перши к поправок, від

рівнянь (53,3) віднімаємо рівняння (53,2):

8X „ _ М у —1ас] z |"'/1 а

[в й |Уі Urn Г 1

З» -u ~Jabl x - [Ьс] z - [М] и

J 1 [6ft] 1 1^1 ' *’

ас) r Jb cI [cdj (53,7)

ccj 1 [сс] И ”

8» _ M V _ М г

ой‘ “ [dd]Xi [dd]yi [ddj *’

Другі поправки обчислюються за такими очевидними фор

мулами: ■

ІдбК ІасК ІadL

5 х , =■ , о Vі — ■! JiO Zr -

....

о//,.

2 [tfrt] [<;а] J [йа] 1

; - °У'1

..

Jbb\lXl [bb] 1 \bb] и

oz «=- ^ o x -

__

!*cl о v ' — —--8й (53,8)

г 2 " [сс] Хі [сс] ' [ccjШ{'

І взагалі в г-му наближенні

Г(7С] ,v [«^1-,.

OJC; — ■ - , UZ-, і І ОНІ I,

‘ « « 1 асг ' [а д ' ’

я И І* ІМ » , fWl>„

'' [bb\°Xi ' ■ [M f ! '[bb\ ‘

<i 1,

И К , IM*,. (53,9)

й2і=, _ . _ йіХі..1_ _ 8у/_І - — ой,.,, v w

^ . Г^/г/J [#лП<ч fcdI л . .

0Иі - - \ш\оХ1- л- т йУ1- }~ ¥ ^ г1'и

Обчислення поправок проводять доти, поки їх числові зна

чення в останньому наближенні будуть настільки малими,

ідо в межах потрібної точності обчислення невідомих ними

можна нехтувати. Остаточні значення невідомих одержують

за формулами

X => Х 1 -Г OATj -І- 0Х2 + . . . - V Ьх-1,

У = У і f О у1 -!- о у 2 + . . . -І- %Уі,

z= zx + ог, -і- oz2 + .. , 4- Ьг-„ (53,10)

и = и[ + out + Ьи2 + ... - і - Ьщ,

де JC|, y\, zь мі обчислюються за формулами (53,2).

' Всі обчислення необхідно робити на арифмометрі або лі

чильній машині в таких двох схемах (т^Зл. 27 і 28), які

для зручності обчислень краще розташовувати поруч.

Спосіб Зейделя відрізняється від способу Якобі лише тим,

що в ньому кожне знайдене наближене значення невідомого

зараз же використовується для визначення наближеного зна

чення наступного невідомого.

С х ем а 1

С х е м а 2

)

X

у

*

a

x

[ab] _[ac]

[ad]

[bb]

[ce]

]dd]

у

[ab]

[be]

[bd]

[aa]

[cc]

[dd]

z

[ac]

[be]

[cd]

[aa]

[bb]

[dd]

11

[ad]

[bd]

[erf]

[aa]

№

[cc]

[«]

S.

o2

X _[£*]

[a a]

5jr,

b x s

у

[W]

[bb]

1

I ^

і

ЬУ

s

2

tvl

c>

^ 1

1

U

1

Sj**3

1 1

0/V«

b u 2

Візьмемо знову систему чотирьох нормальних рів

нянь (53,1):

х-

У -

Z--

[ab]

[ьь]

[ос]

'Ы

И 1., tacL \ad\ И I

[аа]” [аа\

[да] [аа]’

_ № гм] [Ы]

\

ЬЬ

} [ЬЬ]

IW]’

\Ьс 1

[сс 1 [сс]’

ft

_ [a d] \bd\

M L

[ d d f [dd\y \ d d f

\dl

I

\dd V

Знайдемо з першого рівняння наближено шачення невідо

мого Х\, вважаючи, що всі неквадратичні коефіцієнти в ньо

му дорівнюють нулю:

*- _ _ И 1

1 \аау

Перше наближене значення невідомого у\ знайдемо при

умові, що х — Хі, a z = 0 і и = 0; одержимо:

(53,11)

Уг

[аЬ] „ _ [« ]

[ЬЬГ1 [ЬЬ\-

(53,12)

Невідоме z\ знаходимо при умові, що х = хи у уі і

и 0:

\cl\

fee] 1 [се ] [сс]

(53,13)

І, нарешті, невідоме U\ знаходимо при умові, що х ~ Х),

У = Уи Z = Zi.

1

[dd\l [dd]y i [dd]

1

[ddy

(53,14)

Другі наближені значення невідомих одержуємо з рівнянь

(53,1). При цьому в ті члени, які стоять вище діагоналі, бу

демо підставляти перші наближені значення невідомих уі,

21, и\, а в члени, які стоять нижче діагоналі, — значення не

відомих у другому наближенні:

V- _ __И1 _ІЯ£І М 1аі}

2 }аа] 1 1 [яа]’

tab) [be] [bd] [6/]

Л — Ції** (53,15)

г \ach tfecK, и і „ [сі]

1 с с Г 2 [сс ] ' [сс ] И і [сс У

„ r _ І М _ И ] r _ IfMJ

2 \dd\~ [d d f2 И 1 2 W

1 взагалі в і-му наближенні

[au]^i_l [да] [aa] 1 \аа\*

[ab] [fee] [bd] [6/1

Уі1! \Щ Хі І bbfl~' 1 btif1- 1 [bby (53,16)

_

_____

l«l*■

__

lfrcK, М .. _ L ciJ

Z ' “ Icc]Xi [ c c] Ice] 1-1 [cc ]’

„ _ _ І£*] V

1 [dd]Xl [ddy1 [dd] 1 [dd]’

Так обчислюють доти, поки значення невідомих в остан

ньому наближенні мало відрізнятимуться від їх значень у

передостанньому наближенні.

Замість того, щоб обчисляти значення самих невідомих,

краще знаходити поправки до їх значень у першому набли

женні. Ці поправки визначаються формулами (53,5) і (53,6).

Перші поправки, як це легко довести, повинні обчисля

тися так:

Sjc = _ l aA!v _ Ы 2 - M tt v

1 [ааг 1 \aa\ 1 [aa\ l’

>

IflbK l^cl \bd\

0У і_ _ Р і 0Хі “ ІЩг* ~ m u" (53,17)

bz - l—]Sv —{^ u

6Zi “ [cc]6* 1 [cc [cc l " 1*

8a = - \ “*hx - l-^ 5 v - l* h z ^

[ d d fx ' [dd]bZu

де у ь Z\, u\ знаходять за формулами (53,12), (53,13), (53,14).

ГІопразки г-го порядку обчислюють за такими форму

лами:

ЬХі--

З у і =

[ab],

[ас],.

[ad\

'[bb] Xl

— r

-----

\6Уі— і — 7

-----

1 bZi—і — r

-----

,0 U і -і,

[ад] 1 [aa\ [aa\ ’

[6c] ^ [bd]*

~ [bbfZi-'t ~~[bb],jUi ~ u

[ясК [ 6c]

OZi = — [---] OXi — [cC]°> '‘

- { ^ -I, (53,18)

[ad]* [6d]o. [erf] ^

0Ui= m * Xi m f* 1 m 0Zi-

Обчислення поправок припиняють, коли вони стають мен

ші від потрібної точності обчислень невідомих.

Розв’язування рівнянь способом Зейделя зручно вести в.

таких двох схемах (табл. 29 і ЗО).

Таблиця 29

Таблиця ЗІЇ

Схема 1

Схема 2

1

2

3

4

0

1 2

3

V .

X

— '

[ab] 1 [ас]

[bb] j [сс]

[ad]

[dd]

X X,

<іХг

A.v,

у

_ и і

[аа]

\ _ м

j [сс]

[bd]

[dd]

У

Уі

?0'Г

?;V2

Z

_ І асІ

[аа]

[6с]

|66]

—

[erf]

f dd]

2

о z,

Ъг,

........

и

І - І -

І І І

[bd]

[66[

[сс]

—

и

и I

й к,

Ьи„ і

........

‘ 1

[U]

_ И І .

[аа]

[Ы]

[66]

_ L C/L

[сс]

[dl]

[dd]

§ 54. ЧИСЛОВИМ ПРИКЛАД РОЗВ’ЯЗУВАННЯ

НОРМАЛЬНИХ РІВНЯНЬ СПОСОБОМ ЗЕЙДЕЛЯ

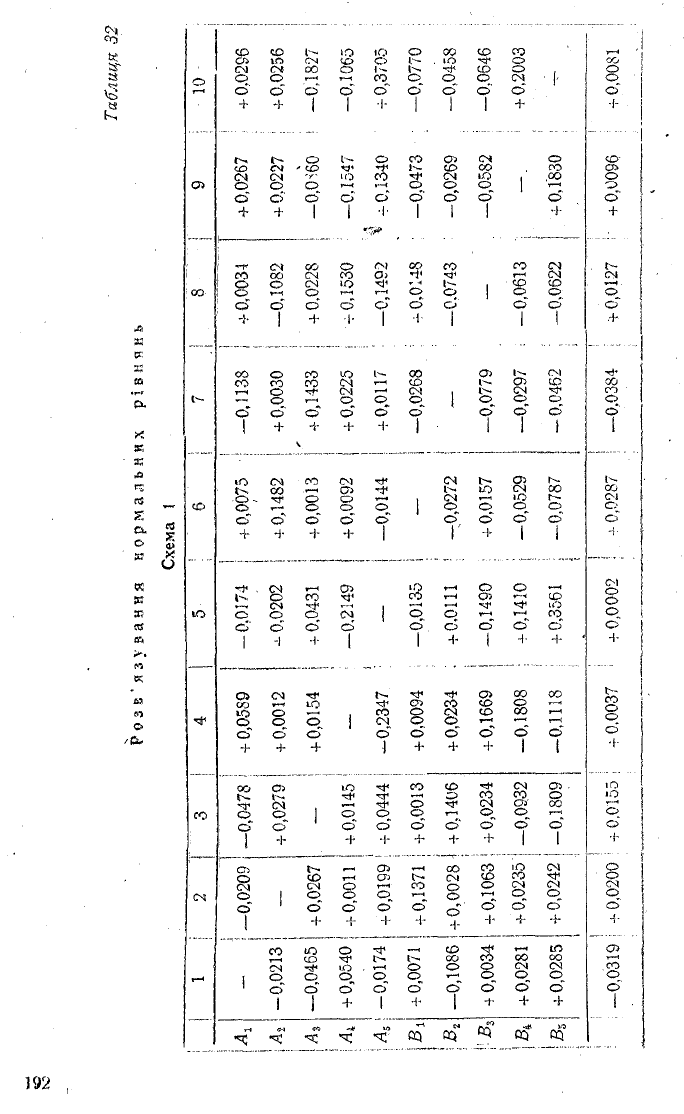
Застосування способу Зейделя розглянемо на числовому

прикладі рішення системи десяти нормальних рівнянь, де не

відомими є коефіцієнти Аи А2, Аз, А4, А5, В,, В2, В3, В4, В

деякої емпіричної функції. Швидка збіжність процесу ітера

ції в цьому прикладі пояснюється звичайно тим, що квадра

тичні коефіцієнти нормальних рівнянь значно більші від не-

квадратичних (табл.31, 32, 33).

§ 55. ВРІВНОВАЖЕННЯ НІВЕЛІРНОЇ СІТКИ

МЕТОДОМ ВРІВНОВАЖЕННЯ ПОСЕРЕДНІХ ВИМІРІВ

(ЧИСЛОВИЙ ПРИКЛАД)

Розглянемо застосування загальної теорії врівноваження

нерівноточних вимірів на конкретному прикладі врівноважен

ня нівелірної сітки (рис. 13).

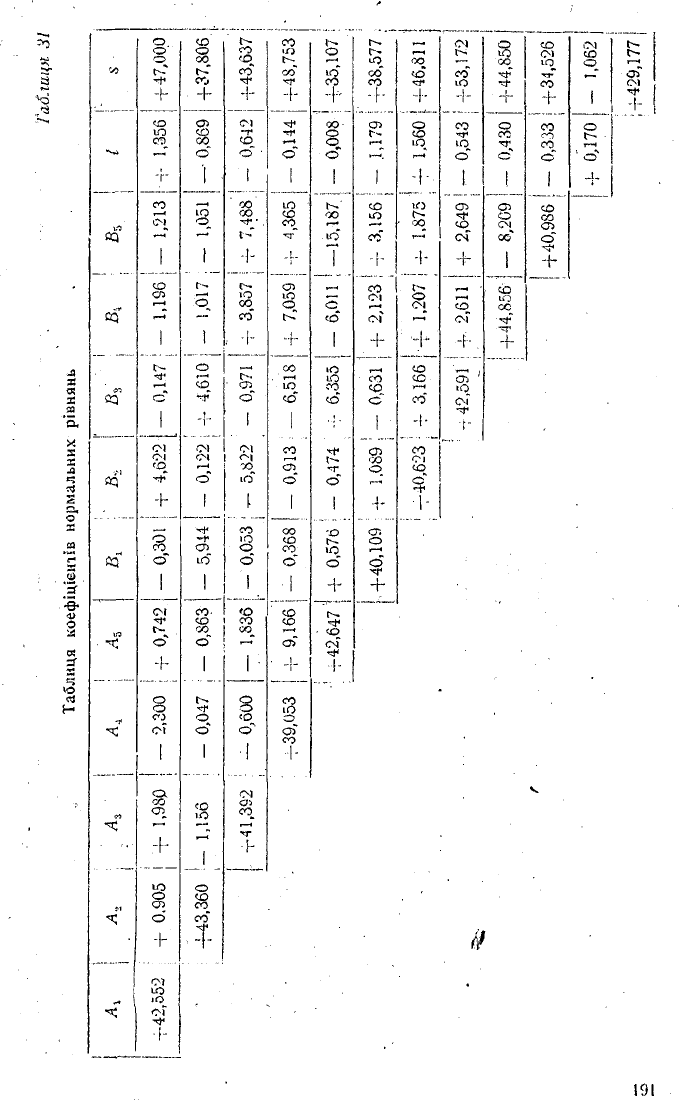
Таблиця коефіціеніів нормальних рівнянь

1—.

Cl

о

ю

CO

—

CO

<o CO

*cr Ю

-I- "Г

СО

ю

o'

05

*=f

о

CS

<o

o\

O';

Ю

О

0

01

+

01

t—

to

0

Г—<

,

a

01

f

Л.

о

_ц

if

£«

hi

S'

a

к!

a,

о

«

о

Г Єй

«

rf

см

Г-н

0>

51

о

о»

со

rt«

Ж!

Ю

о о

о

см

«f

о ' о

о о '

-------

------

со to

»о ю

сл

ю см

со

О

см

СО

о

1-

о о

Г-І

со

о

о" о

о~

4-

1

•I-

о

1-

о

СО

см

" с о

•Ч'

*£

см

«о со

о о о

»—< «—<

о о

о о ' о

+

4-

1 1

см

со

о

о\

со СО

см со о >

о

см

JO

о

*~4

о

t—с

о о о

о

o '

4

1

4-

-I-

I

00

о

со

£>

1^

со со со

см

т—Ч

о

см

о

rH

о

о*

о о о"

о

1

4-

+

н-

О

o '

со

Г-н '

ю

о

со

-tf1

со о , о

о о

^ • 1'

о

о сГ

I 1

+

4-

CO

о>

см

I'-

to со

см

ю

о

о о

о

I I

о

4

00

СО

CM

О

»о

см

со

см

t-. 00

а>

-О -

о о

о

2

о

о~ о"

о~

о

4-

4- 4-

Н-

О

о

Й

о

I

о

4-

о

4*

<х>

о

сГ

О)

t-

СМ

о

4*

ю

•ф

о

+

rf

о

о"

о

+

о

го

,со

о

4-

со

I"-

о

I

СО

о

1--

о>

СМ

о

о"

см

(N

СО

о

СМ

СО

о

см

а>

h-

i>*

to

см 00

00

см ю

г—

см

о

о о о

o '-

г

о

o '

1

о

1

о

05

о

н-

-------

. _.. .

---

-

—

Tf

г -

о>

ю

гИ

05

со

СО

. со

о

см со

о

1 °ч

о

о о

о о о

4-

1

4*

о

5

г-н

o '

со

о

со

Ю

со

о

4-

СГ)

о

см

о

о~

t-

Г~м

СП

«-Н

СО

г-н

1—

см

о

r~i

СО

о о

о

1—1

о о~ о

о

+

4-

+

о

н-

о

о _

о

н-

см

0 5 .

ю

СО со

о

ю

см

OS’

со

о

с> о о

о

+

1

•f-

со

<о см о

СО

со о

о

см см

см

о о

о

о о

о

4 '

4-

4*

со

ю о

—,

СО

1^

І-- 00

см

1.0

Г-Н

о о

о

с>

о

о"

о

Й> СО

О СМ

о о

о~ о

-t- 4*

со

см

о

4-

N /Vs -аР

CQ CQ *4 0^ CCJ

см

о

4-

со

о

о*

4-

со-

о>

о

о"

+

о

o '

4-

о

о*

I

і

СО

о

Бугай П.Т. Теорія помилок і спосіб найменших квадратів

Подождите немного. Документ загружается.