Бугай П.Т. Теорія помилок і спосіб найменших квадратів

Подождите немного. Документ загружается.

міряні кути між напрямами на пункти

/, 2, 3, 4 у всіх можливих комбінаціях по

два напрями в кожній і одержано такі

результати:

(/- 2 ) = 12°ЗГЗЗ",6 = /.„

(/-<?)= 28 21 30,1 ~Z.2,

(/- 4 ) = 140 05 03,4 = Ц,

(.2 -3)=. 15 49 53,5 = L4, (44,1)

(2—#) = 127 33 22,2 = L5,

(3-4)=* 111 43 28,4 = Z.6.

Всі виміри кутів будемо вважати рівноточними.

Завдання полягає в тому, щоб знайти найімовірніші зна

чення кутів х, у, z та їх функцій.

Згідно з рисунком знаходимо такі рівняння помилок:

А' — L l *=vu

х + у — L2 = v2,

x + y+z — L3 = vs,

у — L4 = v 4, (44,2)

y + z - Lr0 = v5,

г - Le=vG.

Всі рівняння цієї системи мають лінійний вид. Отже, мож

на було б зразу приступити до складання нормальних рів

нянь. Однак вільні члени L\, L2, . . ., L6 є величини, які

виражаються семизначними числами, а тому проводити з ни

ми дальші обчислення буде дуже незручно. Щоб уникнути

цього, візьмемо наближені значення кутів Хо, уо, z0 і знайде

мо поправки до них (х), (у), (z), тобто припустимо, що

х = х0 + (х),

У-Уо + Ы . (44,3)

г - г 0 + (г).

Підставимо тепер (44,3) в (44,2):

лг0 + (л ) — L l = v 1,

х0 + (х) + у0 + (у) — L2 = v2,

Хо + (х) + Уо + {у) + z0 + (г) -- Z-з = v3,

Уо + (У) ~ L t- v 4, (44,4)

Уо + (у) + гo + (z) - Lb = vb,

4-(г) - L t = v6.

Рис. 12.

Номери

рівнянь

а ь с /

S аа ab ас

аі

2 3

9 10

1 1

—3,6

—2,6 1 0

-3 ,6

—2,6

1 1 0 -0,1 + 1,9

1 1 0 -0,1

+ 1,9

1 1

-3 ,4 —0,4

1 1 1

-3 ,4

—0,4

0 1 0 6,5 7,5

0 0

1 1 7,8 9,8

0 0'

1,6

2,6 0 0

0 0 0

2 3,0 4,0

3,0

8,8

18,8 3,0

2,0

1,0

-7,1

—1,1

Продовження таблиці 21

Номери

рівнянь

ьь Ьс

bs сс

сі

11 Is

s s .

!4 15 іб 17 18

20 21

0 0

12,96 9,36

6,76

0 —0,1 1,9 0

0,01

-0,1 9

3,61

1 1 -3 ,4 -0 ,4

1 —3,4 -0 ,4

11,56

1,36 0,16

6,5 7,5

0 0 0

42,25

48,75

56,25

1 1

7,8

9,8

7,8

9,8 60,81

76,44

96,04

0 0

1,6

2,6 2,56

4,16 6,76

4,0

2,0 10,8 18,8 3,0 6,0 12,0 130,18

139,88 169,58

Нехай наближені значення невідомих будуть такі:

х0 = 12Г131'30",

у0 = 15°50'00", (44,5)

г 0=111°43'30".

Підставивши, результати вимірів (44,1) і наближені зна

чення невідомих (44,5) в рівняння помилок (44,4), після від

повідних зведень одержимо рівняння помилок в поправках у

такому остаточному вигляді:

(х) -3 ",6 = ®„

(*) + (у) -0 " ,1 = гг2,

(x) + (y) + (z)~ 3",4 —0;І1

(у) + 6",5=--vit (44,6)

(y) + (z) + 7",8 = vs,

(z) + l",6 = ve.

Рівняння помилок треба складати дуже уважно. Будь-

яка помилка, допущена при цьому, приведе до того, що всі

обчислення по врівноваженню спостережень треба буде зро

бити вдруге. Особливо уважно треба визначати значення і

знак вільних членів /,-.

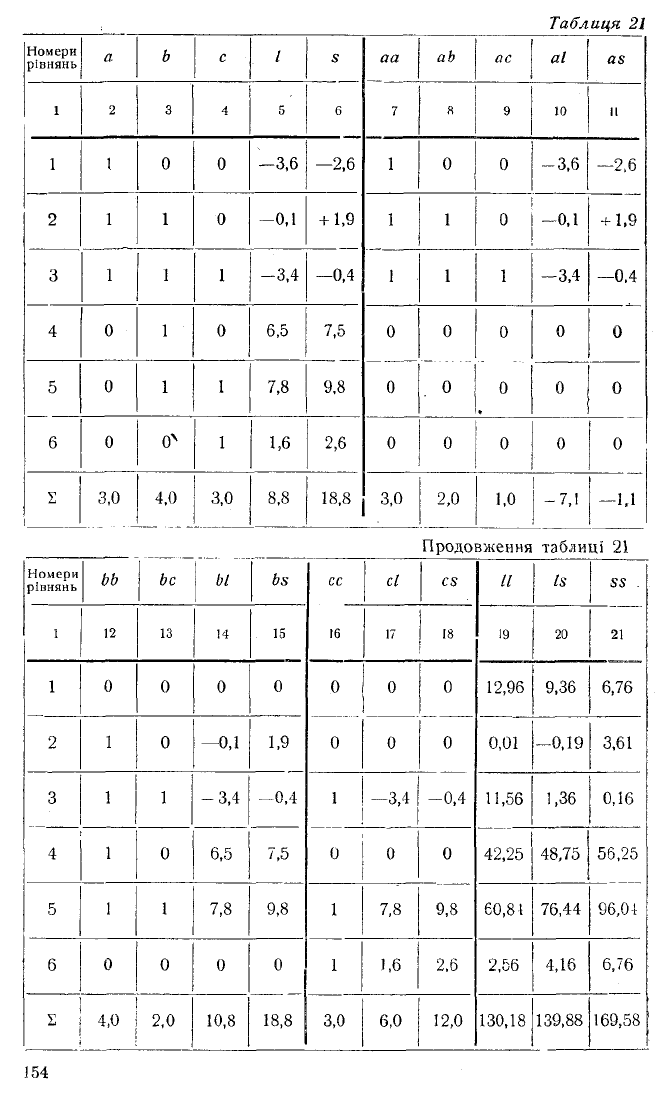
Далі обчислюємо коефіцієнти нормальних рівнянь, що ду

же зручно робити за такою простою схемою, яку ми подаємо

в числовому виді (табл. 21).

В 'заголовку схеми дано загальні позначення коефіцієнтів

і вільних членів рівнянь помилок (44,6): а — при першому

невідомому, b — при другому, с — при третьому та позначен

ня добутків цих коефіцієнтів аа, ab, ... і вільних членів по

рядках.

У рядках 1, 2, 3, . . . , 6 виписані числові значення цих ве

личин. В останньому рядку 2 обчислюються суми по стовп

чиках.

Стовпчики 6, 11, 15, 18, 20 і 21 — контрольні. Як прово

дяться контролі при складанні нормальних рівнянь, буде ска

зано в §45.

Беручи до уваги симетрію коефіцієнтів нормальних рів

нянь відносно діагоналі, на якій стоять квадратичні коефі

цієнти [аа\, [bb], [сс], нормальні рівняння звичайно запису

ють так, як показано в таблиці 22.

Числові значення коефіцієнтів у цю таблицю виписуються

із сумарного рядка Е попередньої схеми.

й]

Ь) с]

S] я]

с]

[а [аа] [ab]

[ас] [аі] [as]

3,0 2,0

1,0

—7,1

—1.1

[Ь №

[6с]

[Ы]

lbs]

4,0 2,0 + 10,8

+ 18,8

[с

[сс] [сі] [cs]

3,0 6,0 12,0

[11]

[/s]

130,18

139,88

[«

[ss] 169,58

Отже, нормальні рівняння в нашій задачі в числовій фор

мі будуть такі:

3.0 (х) +2,0 (у)+ (г)- 7,1=0,

2.0 (х) + 4,0 (у) + 2,0 (z) +10,8 = 0, (44,7)

(*)+2,0(.y) + 3,0(z)+ 6,0 = 0.

Розв’язуючи їх за правилами алгебри, знайдемо:

(■*)= +6",25,

( У ) = -5",67, (44,8)

(z) = — 0",30

і найімовірніші значення кутів:

л; = х0 + (х) = 12°31'36",25,

.У = Уо + Cv)= 1 5Ч9'54",33, (44,9)

z = z0 + (z) = 111°43'29",70.

Щоб знайти найімовірніші поправки vu і>2, • • • , Vn до ре

зультатів вимірів кутів, підставимо знайдені значення (х),

(у), (z) в рівняння помилок (44,6):

При складанні коефіцієнтів нормальних рівнянь, щоб

уникнути помилок, необхідно проводити контрольні обчис

лення. В загальному випадку нерівноточних вимірів при на

явності k невідомих це мо^на зробити так.

Складемо такі контрольні суми з коефіцієнтів і вільних

членів рівнянь помилок:

і -f b t -f + ..

. + tx + /( = S(

Pl^i

2 + b 2 + c2+ .

• Jrt2Jr l2 = S2

p2a2

Р 2^2

n + bn + cn+ .

• + t n + ln = Sn Pn&n РпЬп

Рг* 2

P ntn

Plh

P2l2

Рпі-п

PlS

/>2«2

PnSn

(45,1)

Помножимо їх спочатку відповідно на р\й\, р2а2, . ..,рпап

і добутки підсумуємо:

і + А а A -І-р1аіс1 + . . . + plaltl +plall] '•plalsu

p2a2a2+p2a2b2+ р2а2с2 + . . . +■ p2a2t2+p2a2l2=* p2a2s2t

................................................................................................... (45,2)

P n & n Q n ~V P n & n b n ^ P n d n P n

"V • +

P n Q n t n ~ \ ~

рп&п1п~

P n O - n S f l

\paa\ + \pab\ + [рас] + ... + [pat] + [pal] = [pas].

Контроль обчислень коефіцієнтів досягається тут тим, що

суму [pas] можна одержати двічі: підсумовуючи перший раз

величини по останньому рядку і другий раз — по останньому

стовпчику. Обидва результати повинні бути однакові, чого,

очевидно, не буде, якщо будь-яка величина співвідношення

(45,2) обчислена невірно.

Так само контролюються обчислення коефіцієнтів і реш

ти нормальних рівнянь: множимо суми (45,1) на рФі, р2Ь2, ...

рпЬп, пот^м на РіСх, р2с2,..., рпСп і так далі І, нарешті, на

PiSj, p2s2, . .. , pnsn. Підсумовуючи кожен раз добутки, одер

жимо ще такі контрольні формули:

[pab\ + [pbb] + [pbc] + ... + [pbt

[рас] + [pbc] + [рсс] + . . . + [pet

+ [pbl]-[pbs],

+ [pcl] = [pcs],

pat] +

pal] +

pasj +

pbt] + [pet] +

pbl] + [pci] +

pbs] + [pcs] +,

+ [РЩ+ [pU]-[pts],

+ [ptl]+ [pll] = fp/s],

+ [p£s]-i-[p/s] = [pss].

Суми [pas], [pbs], . .., [pis], [pss] застосовують для

контролю обчислень і при розв’язуванні нормальних рівнянь

у так званій схемі Гаусса—Дулітля.

Якщо виміри будуть рівноточні, то контрольні формули

(45,2) і (45,3) наберуть, очевидно, такого вигляду:

[аа\ + [ab] + [ас\ +.,. + [at\ + [a/] = [as j,

\ab\ + [bb] + [be] +... -i- \bt\ + [bl\ = [6s],

[at] + \bt] + \ct] + ... -r \tt]+ \tl\ = [Zs], (45,4)

\al] + \bl\ -і- \cl\ + ... + \tl\-\- [ZZ] = [/s],

[as] + [fts] + [cs] + ... + [Zs] + [/s] = [ss[.

§ 46 ПРИВЕДЕННЯ РІВНЯНЬ ПОМИЛОК

З НЕРІВНИМИ ВАГАМИ ДО ВАГ, РІВНИХ ОДИНИЦІ

Нехай маємо результати Lі, Ь2, . . . , Ln- нерівноточних ви

мірів функцій незалежних між собою невідомих величин

, х, у, z, , t. Ваги цих результатів нехай будуть р\, р2, . . . ,

рп . Запишемо систему рівнянь помилок у лінійному виді:

а^х) + &1(у) + ^і (z) + ■ •• + tl(u) + ll = v1,

а2(х) -\- b2(y) + c2(z) + . .. + t2(u) + l2 = v2,

.............................................................................. (46,1)

ап(х) + b„(y) -і- сп (z) і- .. . і- tn (/і) + l„ = vn.

В цих рівняннях коефіцієнти а-„ bh . . . , ti є величини ста

лі, і ми можемо вважати їх безпомилковими. Вільні члени,

чк відомо, дорівнюють:

її — f i

(^ 0)

Уоі

^0’ ■ • • ’ «о)

•

Через те що

/ і (-«о. Уо, Z0, . ..,-и0) = con st,

то вільні члени /,• матимуть ті ж самі середні квадратичні по

милки, а значить і ваги, що й результати безпосередніх ви

мірів L,.

Як же треба перетворити вільні члени рівнянь помилок,

щоб ваги їх дорівнювали одиниці? Позначимо ці перетворені

вільні члени через //. Припустимо, шо

Іі'=°-гІг, (46,2)

де а.і — неозначені поки що множники. Це припущення ми

маємо право зробити, тому що між середніми квадратични-

ми помилками і вагами двох величин існує хоч і обернена,

але пропорціональна залежність. Отже, маємо дві величини з

відповідними середніми квадратичними помилками і вагами:

І і, ГПі , Рі ,

І і', Ц, 1.

Знайдемо середню квадратичну помилку функції (46,2):

і Іі = <*г ті , (46,3)

Але, з другого боку, mt = -7^=. Підставивши це значення

У Рі

т,-в (46,3), знаходимо:

лі =VРі , ' (46,4)

W = У Pi h ■

Таким чином, для перетворення вільного члена рівняння

помилок з вагою pt у вільний член /, 'з вагою, рівною оди

ниці, необхідцо перший з них помножити на квадратний ко

рінь з його ваги.

Для приведення рівнянь помилок (46,1) з нерівними ва

гами до ваг, рівних одиниці, необхідно їх коефіцієнти, вільні

члени і поправки vlt и2, .. . , vn , щоб не порушити самих рів-

нсстей, помножити на У рі :

Яі Урі (х) + Ьі У рі (у) + Сі У Pi ( z ) + ...+ ti У рі (и) +

+ h У pi = Vi У рі ,

або, вводячи позначення

at Урі = а’і , Ьі У рі = Ь'і , . . . , ti У рі = і'і ,

Іі Урі = І'і , Vi у Pi = v ’i , (46,5)

одержимо

а і ’(х) + Ь' і (у) + ... + 11 '(«) і - І і’ = Vi'. (46, 6)

Нормальні рівняння, що відповідають цим рівнянням по

милок з вагами, рівними одиниці, можна записати так:

[а'П’\ (х)+[а'Ь’\{у) + . . . + [a't'] (и) + [а’1'] = 0,

\a'b'](x)+[b'b'](y) + , . . + [ЬТ] (и) + [Ь'і] = 0, (46,7)

[а'Г] (х) + [Ь'і] (у) + . . ■ l\t't'] (в)+[*7'| = 0.

Таким чином, рівняння помилок з нерівними вагами зав

жди можна перетворити в еквівалентні їм рівняння помилок

з рівними вагами і врівноваження посередніх нерівноточних

вимірів звести до врівноваження рівноточних.

Коли кількість нормальних рівнянь невелика (2—3), то

їх можна розв’язувати за допомогою детермінантів. Якщо ж

їх буде більше, тоді застосовують інші способи. Найкращим' і

найпростішим з них є спосіб послідовного виключення неві

домих, розроблений Гауссом. Переваги його полягають в од

номанітності процесів обчислень, у наявності поточного конт

ролю їх; при розв’язуванні рівнянь цим способом одночасно

можна знаходити величини, необхідні для оцінки точності

вимірів і результатів врівноваження. Суть цього способу по

лягає ось в чому.

Для спрощення записів і викладу візьмемо систему трьох

нормальних рівнянь:

\аа]х + [ab\y+ [ac]z+ [al] = 0,

[ab]x + [bb\y+ [bc]z+ [Ы] =0, (47, 1)

\ас]х + \bc]y+\cc]z + [сі] = 0.

Визначимо з першого рівняння невідоме х:

[ab] [ас] [аі] р

[аа]У [аа] [аа]' 1

Це рівняння- називається елімінаційним (від лат,

eliminare — виключати). Підставимо тепер його в друге і

третє рівняння системи (47,1):

И]{ - & - й г- й )+[*»ІУ+[»Ф+1 ы\-о;

-[lif } + [6<^]у + М * + И - 0 .

або, розкривши дужки,

[об] [nb] [ab] [ас] [ab] [аі]

[ас] {

y - 4 ^ ^ 4 ^ ; - + {bb\y+{bc}z-Y [Ы] = 0,

[«a] J [аа] [аа]

_[аьпр _ М И ] + [bc}y+[cc\z+ [cl]- 0 .

[аа] [аа] [аа] 1 1 1 1 1

Після зведення подібних членів по невідомих у і z будемо

мати:

[яс][я/]\_п

Введемо тепер такі позначення:

(47, 3)

и -

Тоді рівняння (47, 2) можна записати так:

[ЬЬЛ]у + [ЬсЛ]г + [ЬІЛ] = 0,

[bc.\\y + [cc.\\z+[cl.\\ = Q. (4, ’ 4)

В такий спосіб із системи трьох нормальних рівнянь (47,1)

ми одержали два рівняння з двома невідомими. Невідоме х

виключене. Рівняння (47,4) називаються перетвореними.

Зауважимо, що коефіцієнти рівнянь (47,4) мають ті ж

самі властивості, що й коефіцієнти рівнянь (47,1), а саме:

1) на діагоналі розташовані квадратичні коефіцієнти;

2) коефіцієнти, симетрично розташовані відносно діагона

лі, рівні між собою.

Виключимо тепер друге невідоме у. Для цього визначи

мо його з першого рівняння системи (47,4):

Це — друге елімінаційне рівняння. Підставимо його в.

друге перетворене рівняння (47,4) :

и -п -о,

аоо

Введемо' позначення

(47, 5)

11 П. Т, Бугай

ібі

Після підстановки їх в попереднє рівняння будемо мати

[rc.2]z+[cZ.2]=0. (47,6)

Звідси знайдемо

Підставивши значення z в рівняння Е%, знайдемо невідоме

у. І, інарешті, підставивши z та у в рівняння Е одержи

мо х.

Таким чином, систему нормальних рівнянь (47,1) ми пе

ретворили в таку:'

[аа]х + [ab]y + [ac]z-v [аі] =■*(),

[ЬЬЛ]ул- [bc.\]z-\- [ЫА] =-0, (47, 7)

[cc.2]z+ [cl.2} = 0 .

Ці рівняння називаються еквівалент ни м н. З них і

визначаються всі невідомі.

В загальному випадку система нормальних рівнянь з k

невідомими при нерівноточних вимірах таким самим спосо

бом перетворюється в таку еквівалентну систему рівнянь:

[раа\х-\- [pab]y \- [рас[гл \pad\w + . . . -\-[pat] и4-

-і~ [раї] = 0,

[рЬЬЛ]у-\ \pbcA]z \ \pbd.\]w ■■!- ... і \рЫА \ v.

Л-\рЬ!А]-Л),

\pcc.2\z + [pcd.2]w -і-... ! \pct.‘l]u.\- (47,8)

-і- [pcl.2] = 0,

[pdd.3] «' ч- . . . 4- [pdt.Z]u-\-\pdl.Z] =-■ 0,

{ptt.(k-A)\u + [ptl. (Л— 1)] —0. .

Розглядаючи введені нами позначення (47,3) і (47,5), лег

ко помітити правила їх утворення, а саме:

1) індекси 1 і 2 в символах, що стоять у правих частинах

позначень (47,3) і (47,5), означають той факт, що в резуль

таті перетворень рівнянь (47,1) і (47,4) виключені перше і

друге невідомі відповідно;

2) кожен символ дорівнює двом членам; перший з них

позначається тими ж самими літерами, що й сам символ, але

з індексом на одиницю меншим;

3) другий член є дріб, знаменник якого дорівнює квадра

тичному коефіцієнту, що стоїть при тому невідомому, яке ви

ключається ([аа], [ЬЬА], . . . ), а чисельник дорівнює до,бутку