Бугай П.Т. Теорія помилок і спосіб найменших квадратів

Подождите немного. Документ загружается.

Наявність у результатах вимірів систематичних помилок

можна виявити безпосередньо, аналізуючи значення самих

широт. Справді, візьмемо широти ®3 та <р8 і знайдемо їх різ

ницю:

<Рз- ? 8“ 1".53. (37,2)

Цю величину можна' розглядати як істинну помилку різ

ниці (при абсолютно точних вимірах вона повинна дорівнюва

ти нулю). З другого боку, середня квадратична помилка різ

ниці (37,2) дорівнюватиме:

пи

/По

± |/( а 2 0 ) 2'+(0,І8)і = + 0,"27.

Отже, дійсна помилка різниці 'f3—fs в п’ять з лишком ра

зів більша від її середньої квадратичної помилки, виведеної

за середніми квадратичними помилками окремих результатів.

Приклад 3. За поданими в таблиці 15 результатами ви

мірів кута знайти його найімовірніше значення, середні квад

ратичні помилки окремих вимірів і остаточного результату.

За ваги результатів взято числа прийомів, зменшені в два

рази.

Таблиця 15

№

Число при-;

йомів k

Ваги

Р ~2

рг

5 рЬ

р 6*

V p

56°43'35",5

2,5

30,0 75,00 +0,74

+8,88 6,5712 0",56

2 34,7

12 6

1,7

10,2

17,34

-0,0 6 -0,3б! 0,0216 0,79

3 34,<5

',6

8,0

12,80 -0,16

-0,80

0,1 *80

0,86

4 34,3

1,3

3,9

5,"7

-0,46 -1,38 0,6348

1,12

33,4

0,4

1/5

0,64

-1,36

-5,44

7,3984

0,96

6 34 4

2,5

1,4

3,5 4,90

-0,36

--0,90

0,3240

1,22

/«

56 43 33,0

32,5

57,2

115,75

+ 8,88

\Р*\

\І>\

+ 1.76

—8,88

,Ц

56 43 34,76

15,0780

Контроль:

\Р Щ И5.7Г)

327 L 84

32,5

15,08.

Середня квадратична помилка одиниці ваги

„ - i j / E f l . + j і 1»,93.

Середня квадратична помилка середнього арифметично

го по вагах

/И0--! / = '■()",34.

' V \Р] ~

Середні квадратичні помилки окремих результатів обчис

лені за формулою

В даному прикладі ми не маємо даних для визначення

середньої квадратичної помилки (її одиниці ваги за формулою

(32,10) або (37,1) і не можемо порівняти її з помилкою [л, об

численою за формулою (33,9). Тому ми не можемо судити

про узгодженість окремих результатів'вимірів. У цьому й по

лягає принципова різниця між двома випадками обробки не-

рївноточних вимірів, про які ми говорили на початку цього

параграфу.

§ 38. З А Д А Ч І Н А З А С Т О С У В А Н Н Я Т Е О Р ІЇ П О М И Л О К

Н Е Р І В Н О Т О Ч Н И Х В И М ІР ІВ У Г Е О Д Е З И Ч Н І Й П Р А К Т И Ц І

Задача 1. Змайти вагу виміру лінії довжиною D, якщо вагу

результату виміру лінії довжиною d прийняти рівною оди

ниці.

Позначимо ваги даних ліній відповідно через pDi pd . Зтід-

ио з формулою (28,6) середні квадратичні помилки вимірів

цих ліній будуть

til'd — i.V'Yd і ~ І о. (38,1)

Беручи до уваги основне співвідношення (29,2) між се

редніми квадратичними помилками вимірів та їх вагами,

одержимо

Рр т йг . y d

Р<і~*то г н-о2’

звідки

P d _ d

Ра ~ D '

Якщо pd =“1, то

Pd = £•

(38.2)

(38.3)

Отже, вага результату виміру лінії обер

нено пропорціональна довжині лінії.

Задача 2. Знайти вагу ро суми перевищень нівелірного

ходу довжиною А якщо вагу ра суми перевищень нівелір

ного ходу довжиною d прийняти рівною одиниці.

Згідно з формулою (28,10) середні квадратичні помилки

сум перевищень даних нівелірних ходів дорівнюватимуть:

md= ± \V d і mD= ± v Y D . < (38,4)

Знаходимо відношення ваг:

р р т* a d

Pd m*D ® " (38,5)

Якщо

P d =

1 , TO

= (38,6)

Отже, вага суми перевищень нівелірного

ходу обернено пропорціональна довжині

ходу.

Довжини нівелірних ходів можна виразити через кіль

кість станцій п, а саме

d = 2pnd, D = 2pnn,

де р— однакова для всіх станцій віддаль від нівеліра до

рейки. Тоді формула (38,6) набере такого вигляду:

Рп=П± (38,7)

Таким чином, вага суми перевищень ніве

лірного ходу на п станцій обернено про

порціональна кількості станцій.

Задача 3. Визначити середню квадратичну помилку т

одного виміру кута за кутовими нев’язками полігонів, пода

ними в таблиці 16.

Якщо вагу одного виміру кута прийняти рівною одиниці,

то згідно з формулою (35,7) вага суми щ кутів і-го поліго

на дорівнюватиме:

Номери

ПОЛІГО

НІВ

Нев’язки

Кількість

кутів п

Ваги

Р - ~

да!

pw2

1',8

1,11

3,24 3,5964

2,2

0,83 4,84 4,0172

3 3,5

0,67 12,25 8,2075

0,8

5 2,00 0,64 1,2800

0,2

1,25

0,04 0,0500

1,5

1,43

2,25

3,2175

2,0 18

0,56

4,00

2,2400

1,2

1,67 1,44

2,1708

9 2,8 14

0,71 7,84 5,5664

2.5

1,00

6,25

6,2500

S-= 46,5958

Кутові нез’язки WЬ W2, ■ ■ ■ , Wk , де k — кількість поліго-

ніз, можна розглядати як істинні помилки сум кутів поліго

нів. Тому середню квадратичну помилку [і одиниці ваги мож

на одержати за формулою (32,9):

fw? w* wk "

У --пі

1г - k — k

За числовими даними таблиці 16 одержимо:

Iа = ± У ':'

46,5958

■ +

У 4,

65958 -

2',2,

(38,9)

(38,10)

“ - ± р % - ± 0'-7-

Задача 4. Зробити оцінку точності геометричного нівелю

вання за нев’язками полігонів, поданими в таблиці 17.

Ваги сум перевищень по кожному зімкнутому нівелірному

полігону обчислюємо за формулою

Номери

поліго

нів

Нев’язки

/ в мм

Кількість

станцій п

Ваги

100

р “ п

/ 5

P f

+ 8,2

1,32

67,24 88,7568

2 - 6,5

2,22

42,25

93.7Р50

+ 4,9 54

1,85 24,01 44,4185

— 7,5

108

0,93

56,25 52,3125

-11,4 124

0,81 129,96

105,2676

+ 5,3

1.47 28,09

41,2923

-12,8

115

0,87

163,84

142,5408

+ 7,3 93

1,08

; 53,29 57,5532

— 9,7

1.23 j 94,09

115,7307

+ 13,2 138

0,72 174,24

125,4528

; V

867,1202

де щ — кількість станцій в t-му полігоні. Отже, вагу р — 1

буде мати полігон на 100 станцій. Приймаючи нев’язки Д. за

істинні помилки сум перевищень, середню квадратичну по-,

милку |х одиниці ваги обчислюємо за формулою (32,9):

l / S

V nj

f Z

I ;--„L +

fjr

/ Ш

Підставивши числові дані задачі, будемо мати

[і-+±9,3 мм.

Середня квадратична помилка виміру одного 'перевищен

ня на станції

0:,9 мм.

Задача 5. Один і той же кут вимірявся різними інстру

ментами. За даними в таблиці 18 значеннями кута та середніми

квадратичними помилками т одного виміру, одержаними з

вимірів цими інструментами, знайти найімовірніше значення

кута і визначити його середню квадратичну помилку М0.

№

Резуль

тати ви

мірів

1 КІЛЬКІСТЬ

j прийомів

М Мг

Ваги

*>~м'

рг

ргг

рЬг

58°36' 12" 12

+3",0

+0",е 0,81

1,23

2,46 4,92

-2,5

—3,075

7,6875

16 9 ±5,0 ±1,7 2,89

0,35

6 2,10 12,60

+ 1,5

+ 0,525

0,7875

±4,0

±1,6

2,56

0,39

0 0

-4,5

-1,755

7,8975

±3,5

±0,9

0,81

1,23 4

4,92 19,68

-0,5

-0,615

0,3075

10 ±4,5 ±1,4 1,96

0,51

1,53

4,59

-1,5

-0,765

1,1475

20 ±3,5

±0,8

0,64

1,56

12,48

99,84

+3,5 + 5,460 19,1100

А>

58 36 10

5,27

23,49

141,63

[р5*] -

36,9375

\Р\

+ 4,5

58 36 14,5

и, , .

...

....

...

____

....

.....

Контроль:

[/?52] - [ps2] - 141,63- 55JvJ0' - 141,63-104,70 =■ 36,93.

Дані в таблиці значення 'кута являють собою середи*

арифметичні, виведені з відповідної кількості прийомів. Че

рез те, що середні квадратичні помилки т одного виміру ку

та різними інструментами не є однакові, то за ваги резуль

татів І не можна брати величини, прямо пропорціональні кіль

кості прийомів. Для їх обчислення необхідно спочатку знайти

середні квадратичні помилки М середніх арифметичних І за

формулою

де ki — кількість прийомів, а потім обчислити ваги

За даними задачі найімовірніше значення кута дорів

нюватимє:

£o = V J f ^ J = 5 8 °3 6 '1 4 ",5

з середньою квадратичною помилкою

мп

= + і / Т М І І І - ’ _ + т / ? ^ ? 3 7 5

г,

± У (rt-l)LpJ - К 5-5.27 1 1 ,Z-

Задача 6. Між чотирма точками А, В, С і D з невідомими

висотами було прокладено шість нівелірних ходів (рис. 9).

Суми перевищень і кількість станцій по цих ходах дано в

таблиці 19, причому знаки перевищень позначені в напря

мах, показаних стрілками. Необ

хідно врівноважити перевищення

по ходах, тобто виправити їх так,

щоб у кожному зімкнутому полі

гоні алгебраїчна сума переви

щень дорівнювала нулеві.

Щоб врівноважити ці ходи, за

стосуємо так званий спосіб ек

вівалентної заміни.

Як відомо з попереднього ви- (

кладу (див. § 38, задача 2),

вага суми перевищень нівелірного ходу на п станцій оберне

но пропорціональна числу станцій, тобто

Рг

_х_

~п,

де і — номер даного нівелірного ходу, X— коефіцієнт про-

порціональності, прийнятий при обчисленні ваг. Якщо буде ві

дома вага ходу р, то можна теоретично визначити і кіль

кість станцій п, яка відповідає цьому ходу з вагою р. Маю

чи це на увазі, врівноваження даної нівелірної сітки про

водимо так.

Візьмемо нівелірні ходи 1 і 2. Суми перевищень hi і h2

відповідно по кожному з них дають величини перевищення

точки А над точкою D з вагами

X , х

. * - " 5 Г 'Л - Ї Г -

Найімовірніше значення перевищення hEl точки А над

точкою D знаходимо за формулою середнього арифметично

го по вагах, тобто

, hlPt + h^p,

Е і Р і + Р г

з вагою

Ре^ Р і+Рі-

Таким чином, два нівелірні ходи між точками А і D ми

можемо замінити одним уявним ходом Еі з сумою переви

щень /ц , вага якої дорівнює ■

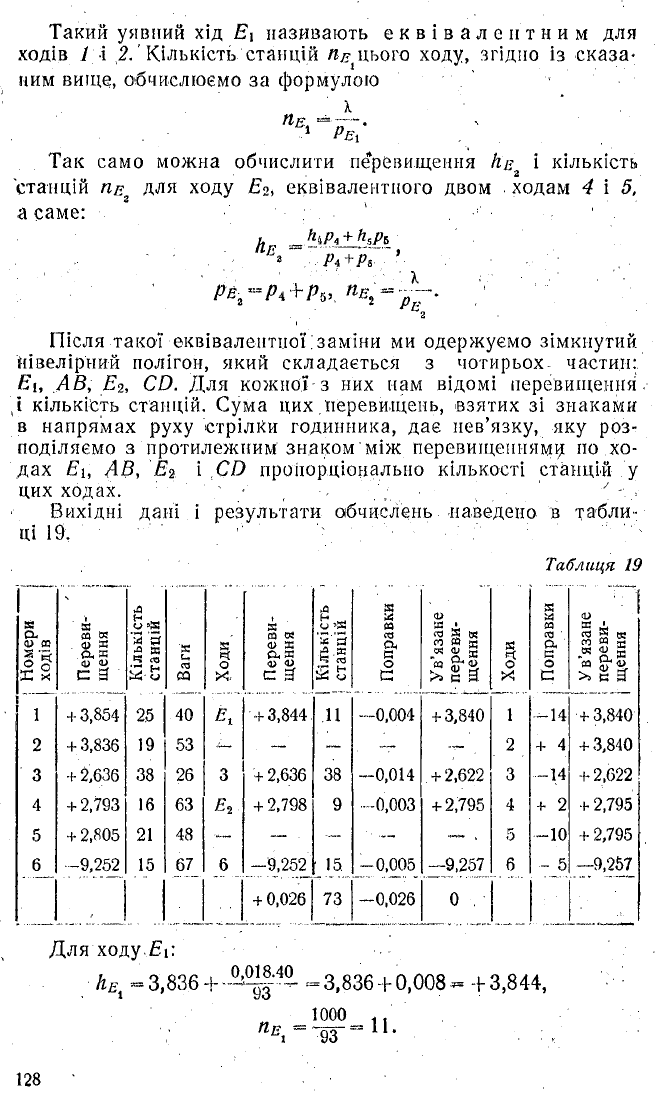
Такий уявний хід Е\ називають еквівалентним для

ходів І і 2.' Кількість станцій цього ходу, згідно із сказа

ним вище, обчислюємо за формулою

X ‘

til-- - — .

1 Рій

Так само можна обчислити пє*ревищєння А я і кількість

станцій пе для ходу Е2, еквівалентного двом ходам 4 і 5,

а саме: •. ' 1

’.-а +аГГ*-

Рё ~ Р ^ Р ьк ПЕ.

: x

Pi:..

Після такої еквівалентної:заміни ми одержуємо зімкнутий

нівелірний полігон, який складається з чотирьох частин:

Е[, АВ, Е2, CD. Для кожної-з них нам відомі перевищення .

,і кількість станцій. Сума цих .перевищень, взятих зі знаками

в напрямах руху стрілки годинника, дає нев’язку, яку роз

поділяємо з протилежним знаком між перевищенням^ по хо

дах Еі, АВ, Ег і CD пропорціонально кількості станцій у

цих ходах. ' • , - ; ‘ у

Вихідні дані і результати обчислень наведено в табли

ці 19. ■ ■■

Таблиця 19

Номери j

ходів !

03 «

<у Я

<Х я

с 3

Кількість

станцій

Ваги

Переви

щення

: КІЛЬКІСТЬ 1

І станцій

Поправки ;

1 Ув’язане

переви-

' щення

Ходи

та '

О.

Ув’язане

переви-

j щення • ‘ j

+ 3,854

2.5

+ 3,844

-0,004

+ 3,840

-1 4 + 3,840

+ 3,836

1 9

—

— .

4 + 3,840

-1-2,636

26 3

+ 2,636

38 -0,014

+ 2,622

-1 4

+ 2,622

4 + 2,793

16 63

Ег + 2,798

-0.003 + 2,795

+ 2

+ 2,795

5 + 2,805

—

— ,

5 -1 0 + 2,795

6 -9,252 15

6 -9,252

+ 0,026

-0,005

-0,026

-9,257

0 .

- 5

—9,257

Для ходу.£і:

hEi - 3,836 + - ° Я |42- = 3і836 + 0)008

Ля

1000

: 93 =

11.

Для ходу Е2:

hEi = + 2,793 + 001112-48 = + 2,793'+ 0,005 = 2,798,

Поправка а0, що припадає на одну станцію,

а°= Тз~ = ~'*-*»356 мм.

Задача 7. Між реперами А, В,

С і D з відомими висотами про

кладено п’ять нівелірних ходів,

які утворюють дві вузлові точки

М та N (рис. 10). Треба ув’язати

ходи і знайти висоти точок М і N.

Задачу можна розв’язувати

різними способами. Один з них

такий.

Рис. 10.

За відомими висотами точок А і В і перевищеннями по

ходах 1 і 2 знаходимо висоти точки М:

Середнє вагове значення висоти точки М, обчислене по

цих ходах, дорівнюватиме:

з вагою PEi =PiJrp2- Цій вазі теоретично відповідатиме

кількість станцій

Отже, нівелірні ходи 1 і 2 ми замінили одним уявним ек

вівалентним ходом Ех з вагою рв і кількістю станцій пег

Таким чин^м, дану нівелірну сітку з двома вузловими точ

ками ми перетворили в сітку з однією вузловою точкою N.

Остаточну висоту її Ядг знаходимо за формулою середнього

арифметичного по вагах з трьох ходів £і+3, 4 і 5, а саме:

Рі + НіРї

Р і + Р г

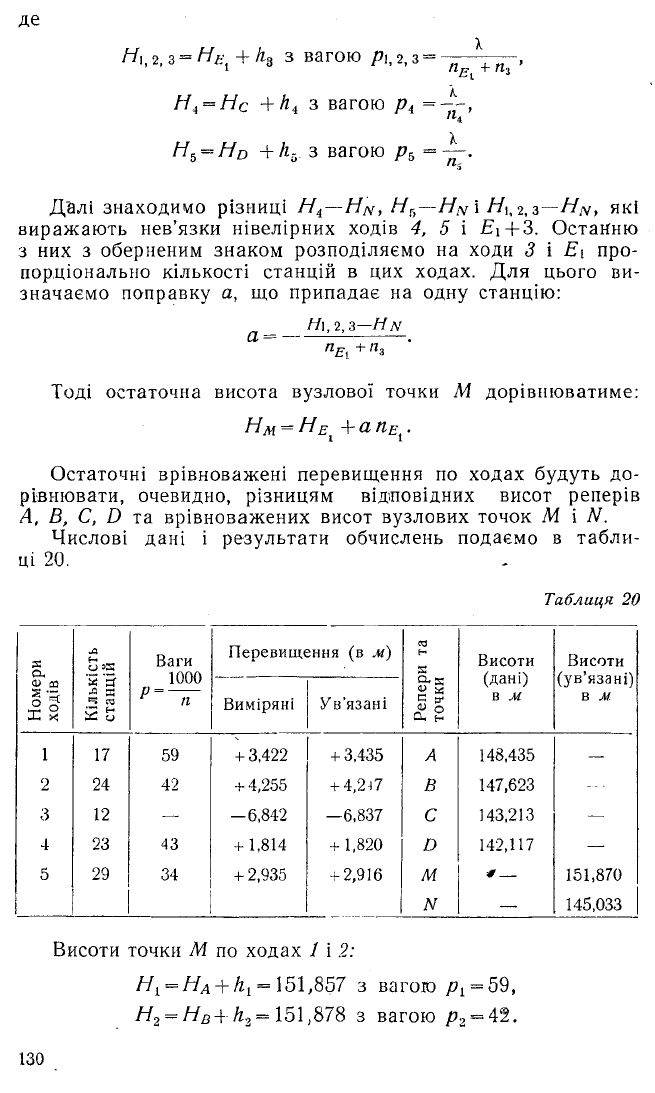
Н\'ї,г = НЕ, +hs з вагою Рі,г,з= „

Е\ %і

Н4 = НС +hi з вагою

П4

НЪ = Н0 +А5 з вагою р5 =-” •

Далі знаходимо різниці H^—Hn, Hb—HN і H\^tz~HN, які

виражають нев’язки нівелірних ходів 4, 5 і £і + 3. Останню

з них з оберненим знаком розподіляємо на ходи 3 і Еі про-

пордіонально кількості станцій в цих ходах. Для цього ви

значаємо поправку а, що припадає на одну станцію:

Н \ ,

2, з

— H n

а =

------------------

пЕі + П*

Тоді остаточна висота вузлової точки М дорівнюватиме:

Н м = Н еі + (і Пеі •

Остаточні врівноважені перевищення по ходах будуть до

рівнювати, очевидно, різницям відповідних висот реперів

А, В, С, D та врівноважених висот вузлових точок М і N.

Числові дані і результати обчислень подаємо в табли

ці 20.

Таблиця 20

Номери

ходів

Кількість

станцій

Ваги

1000

р - ~

Перевищення (в м)

Репери та

точки

Висоти

(дані)

в м

Висоти

(ув’язані)

в м.

Виміряні Ув’язані

17 59 + 3,422

+ 3,435

148,435

—

24 42

+ 4,255

+ 4,247

147,623

---

3 12

—

—6,842 —6,837

143,213

—

4 23 43

+ 1,814 + 1,820

142,117

—

5 29

34 + 2,935

+ 2,916 М

151,870

N — 145,033

Висоти точки М по ходах 1 і 2:

Н1=На + Ь1 = 151,857 з вагою pL = 59,

Н2 = Нв + h2 = 151,878 з вагою