Бугай П.Т. Теорія помилок і спосіб найменших квадратів

Подождите немного. Документ загружается.

Задача 5. Знайти середню квадратичну помилку т-і суми

перевищень при довжині нівелірного ходу D = 2np, де п —

кількість станцій, а р — віддаль від нівеліра до рейки, якщо

середня квадратична помилка відліку по рейці дорівнює

± т.

При нівелюванні з середини перевищення одержують як

різницю двох рівноточних відліків:

h = a—b.

Середня квадратична помилка mh перевищення дорівнює:

mh = ± т У 2. (28,7)

Середня квадратична помилка суми перевищень дорівнює:

/Яї = ±тУг2п. (28,8)

Але я = ~|р - Підставивши це значення в (28,8), одержимо:

тv - ±т ]/ °? - ± у ~ У О. (28,9)

При даних умовах нівелювання і приймаючи т і р одна-

ковими для всіх станцій, величину можна вважати ста-

> р

лою. Позначимо її через v. Тоді формулу (28,9) можна запи

сати так:

пн = ± v УТ). (28,10)

Звідси випливає, що випадкові помилки при нівелюванні

нагромаджуються прямо гіропорціонально квадратному ко

реню з довжини нівелірного ходу.

Задача 6. Знайти середню квадратичну помилку остаточ

ного значення кута, який вимірявся при двох положеннях

вертикального кола способом повторень, якщо середні квад

ратичні помилки візування і відліку по верньєру дорівнюють

відповідно mv і гпь .

Щоб виміряти кут п повтореннями при одному положенні

вертикального кола, необхідно зробити два відліки по лімбу

і 2п візувань зоровою трубою. Якщо середня квадратична

помилка відліку по одному верньєру дорівнює гпь, то по

милка . відліку по лімбу, взятого як середнє арифметичне з

відліків по двох верньєрах, буде —-

>' 2

Беручи до уваги помилки , візування, квадрат середньої

квадратичної помилки різниці відліків по лімбу, яка дорів

нює /г-кратному значенню вимірюваного кута а, складати

меться з таких помилок: . 1

(

та \2 / т \2

■~=.j + ^ 2 ~ j +т °2+ /я'°2 + • • • 1 т»

пі,.

\у 2 / \у 2 ! —

-------

2 п

= /гавг [- 2nmv2, (28Д1)

звідки

тп^ ± У 2 п (т с> : т/ ї ) . (28,12)

Помилка одноразового кута буде в п разів менша:

. t28.13)

т„

І, нарешті, середня квадратична помилка остаточного

значення кута а, взятого як середнє арифметичне з резуль

татів вимірів його при двох положеннях вертикального кола,

дорівнюватиме:

___

____

*.-±/М ”'г+£Г)- <28’14)

Задача 7. В трикутнику ABC були виміряні сторона с і

кути (З і у (рис. 1). Знайти середню квадратичну помилку

ть сторони Ь, якщо середні квадратичні помилки кутів § 1 т

в радіанній мірі дорівнюють відповідно т$ і тл.

За теоремою синусів

, с sinft

sin-/ • (28.15)

Знаходимо часткові похідні функції (28,15):

db sin В sinS b db Ь

ъ- = --—; але

, отже, (28 16)

де sin f snif с ’ де с ’

db с cosB с b db , , a _ v

Ю — але ------ = -.-7Г, отже, ™ ■■= b ctgB; (28 Ш

dp siny sin^ sinp’ ’ dp , ;

db csinBcosY - db sinS sinS ,

, = - — або -j-=— с cter; але с .--- = 0,

ду sin-2 у 0‘f sin^ 1 sui'f

отже, ftctgT. (28,18)

Підставивши (28,16), (28,17) 1 (28,18) в загальну формулу

(18,14) і виразивши середні квадратичні помилки /ир і т т в

кутовій мірі, одержимо:

ш, - ± ь V f T a (» .

с р р

де р" — число секунд в радіані.

Цю задачу можна розв'язати ще так. Візьмемо натураль

ний логарифм функції (28,15):

In 6 = lne + In sinp — Insiny . (28,20)

Знаходимо далі повний диференціал від (28,20):

Т “ 7 + _ ctgTrfy,

або, замінивши диференціали конечними, але малими помил

ками, матимемо

= й ( т + ctSPAP — ctgrAr}- (28,21)

Тут помилки др і Ду повинні бути виражені в радіан-

ній мірі.

Формула (28,21) цілком подібна до формули (18,10). Вона

виражає помилку функції (28,15) при певних фіксованих

значеннях Де, Др, Ду помилок аргументів. Для переходу

від помилки (28,21) функції до її середньої квадратичної

помилки (18,14) необхідно помилку функції Дb і помилки ар

гументів Дс, Ар, Д-f замінити квадратами їх середніх квад

ратичних помилок і коефіцієнти при них (часткові похідні)

теж взяти в квадратах. Тоді

шьг = b2 { + ctg2 р щ2 + ctg2? m T 2} ,

або, виразивши і отт в кутовій мірі, одержимо:

лг2ь = й2 { -- -f ctg2 р {-?*- )2 + ctg2Y (-"-V )2} . (28,22)

Задача 8. Перевищення h між двома точками при гео

дезичному нівелюванні визначається за формулою Л = / tga.

Знайти середню квадратичну помилку /ге* перевищення, якщо

середні квадратичні помилки віддалі І і кута нахилу а до

рівнюють відповідно ті і пга.

Прологарифмуємо дану функцію:

In A = ln/+lntga. (28,23)

Повний диференціал цієї функції буде

d h ^ d l d a d l

d o .

h I t g a

cos2 a / ^ sin 2a ’

або, замінивши диференціали конечними малими помилками,

ДЛ = Д£ 2Да (28,24)

h I sin‘2а

Переходячи під помилок до середніх квадратичних по

милок, будемо мати

звідси

( ^ \2= ( "ІіУл. (_ 2 пн" 'і3

І А і W / ' I p'"sin 2а 1 '

п . . І ті- , і' 2 та" \ 2 1

mh* = h2 I -j, -г ( ,/,sin2r( ) (28,25)

Задача 9. Дано середні квадратичні помилки на 1 км

ходу геометричного нівелювання: випадкового впливу --

+ т/ і систематичного — + т'а. Знайти середню квадратичну

помилку іпь сумарного впливу для нівелірного ходу довжи

ною L км.

Вважаючи, що вплив випадкових помилок при нівелю

ванні зростає прямо пропорціонально квадратному кореню

з довжини ходу, а систематичних помилок — прямо про

порционально його довжині, для ходу довжиною L будемо

мати

т е= т .’у l

Згідно з цим

(28,26)

та = + т / L.

ті. - ± \ / m,'*L + m / ‘L2. (28,27)

Задача 10. Знайти середню квадратичну помилку виміру

лінії, якщо середня квадратична помилка випадкового впливу

на одиницю довжини дорівнює |х, а систематичного впли

ву — а.

Позначивши довжину лінії через D, середню квадратичну

помилку тг в результаті виміру лінії, обумовлену впливом

лише випадкових помилок, знайдемо за формулою (28,6):

m6=+;xj/D . (28,28)

Беручи до уваги, що вплив систематичних помилок зро

стає прямо пропорціонально довжині лінії,

m ^ ± c D . (28,29)

Отже, сумарний вплив випадкових і систематичних дже

рел помилок дорівнюватиме:

то2 = !і2 D + о2 D2,

'21

звідки

то

= ± j / ti3D + о2£>2. (28,30)

Відносна помилка довжини ліній буде

-т£ - У - б + * ‘ <28’31>

Гіри даних умовах вимірів ліній і для даного вимірю

вального приладу величини ji і з можна вважати сталими.

Отже, при цій умові з формул (28,30) і (28,31) виходить, що

із зростанням довжини лінії абсолютна помилка її виміру

зростатиме, а відносна зменшуватиметься. Чим довша лінія,

тим менша частка випадкового впливу, і навпаки.

Задача 11. Дано середню квадратичну помилку b

логарифмі довжини лінії L. Знайти відносну помилку b

довжині цієї лінії.

Візьмемо функцію

_у =■ 1 n Z,. (28,32)

Якщо лінія має відносну помилку тоді її абсолютна,

або лінійна помилка дорівнюватиме:

- 4". (28,33)

Знайдемо тепер середню квадратичну помилку функції

(28,32) за формулою (18,14):

™ » - ± У { ! - о п £ > Г ( 4 - Т ,

або

м L М ,00

l — £ • дг /V ’ (28,34)

де М = 0,4343 — модуль переходу від натуральних логариф

мів до десяткових.

Якщо migi дано в одиницях сьомого знака логарифмів,

то формулу (28,34) необхідно записати так:

(28,35)

10" N к '

звідки

(2 8 >3 6 >

Використовуючи формулу (28,36), можна розв’язати і

обернену задачу, а саме: знайти середню квадратичну по

милку m\SL, якщо відома відносна помилка 3 формули

(28,36)

_ М-107 . .

«ig/. = - -у- ■ (28,37)

Задача, 12. Знайти середні квадратичні помилки прирост

ків координат Дх = s cos а і Ay = ssina, якщо відомі середні

квадратичні помилки ms і та довжини лінії s і дирек-

ційного кута a: s + ms = 205,40 ± 0,12 м, а +та = 34°30' ± і',5.

Розв’яжемо цю задачу спочатку в загальному виді.

Для цього за формулою (18,14) знаходимо середні квадра

тичні помилки функцій:

Підставивши ms, та і значення часткових похідних функ

цій (28,38) у формулу (18,14), одержимо:

де помилка та виражена в радіанній мірі.

Цю задачу можна розв’язати ще за допомогою таблиць

логарифмів. Прологарифмуємо функції (28,38):

Через те, що аргументи s, а і залежні від них прирост

ки Ах та Ду мають помилки, то матимуть помилки і лога

рифми величин, що входять у формули (28,40). Позначимо

ці помилки через mtgbX, migДу, migs, /rcigCosa і mlgs-m*.

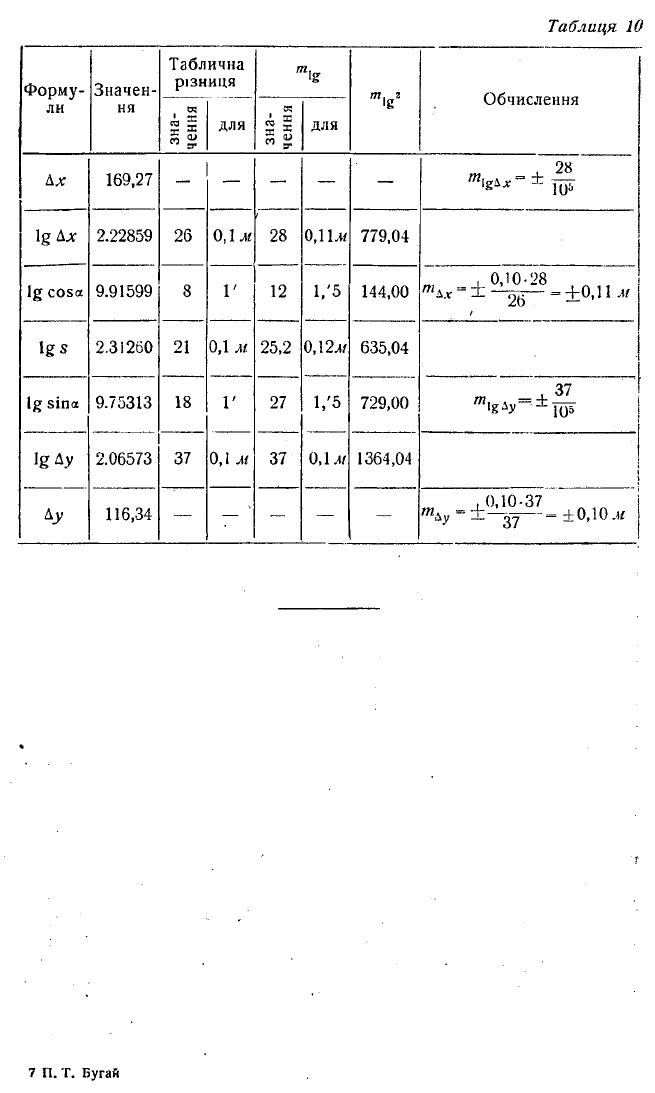
Обчислення за цими формулами зручно провадити в схемі

(табл. 10).

За числовими даними задачі знаходимо mig!iX = ±28,

/Яігду = ± 37 в одиницях п’ятого знака логарифмів. Цим по

милкам відповідають помилки в приростках координат

тьх= ±0,11 м і /яду = ± 0,10л.

Ax = S COS а,

Ay=ssitl а.

(28,38)

Маємо

(28,39)

lg A x = l g S + lgCOS а,

lg Ду = lgs± lgsin а.

(28,40)

Тоді

Ьх— ^ “igs ± ^i2]gcosa,

(28,41)

Форму

ли

Значен

ня

Таблична

різниця

тІ2

« V Обчислення

зна

чення

для

зна

чення

для

Ах

169,27

" W * S

lg Ах

2.22859 26

0,1 м 28 0,11 м

779,04

lg C O sa 9.91599 8

V 12

1,'5

144,00

, 0,10-28

gig— = ±0,11 иг

lg s 2.31260

ОД м

25,2

0,12 м

635,04

lg sina

9.75313

1/5

729,00

«7

lg Ду

2.06573

0,1 м 37 0,1л 1364,04

116,34

,0,10-37

m4y“ + —37— = ±0,10 .и

Г л а в а II

НЕРІВНОТОЧНІ ВИМІРИ

§ 29. НЕРІВНОТОЧНІ ВИМІРИ ТА ЇХ ВАГИ

Досі ми розглядали питання обробки результатів рівно

точних вимірів, тобто таких, які були проведені однаково

точними інструментами, однаково досвідченими спостеріга

чами, при однакових приблизно зознішніх умовах та ін. Ана

лізуючи результати таких вимірів однієї і тієї ж величини,

у нас не було будь-яких підстав вважати один з них кра

щим, а другий гіршим, тому що обидва вони були одержані

при однакових умовах, яким відповідає одна і та ж середня

квадратична помилка т одного виміру. При виводі остаточ

ного значення вимірюваної величини ми брали просте се

реднє арифметичне і вважали його найімовірнішим значенням

вимірюваного об’єкта.

Однак часто окремі визначення (чи то за допомогою ви

мірів, чи шляхом обчислень) однієї величини (або різних,

але однорідних) проводяться при різних умовах — неодна

кової точності інструментами, різними методами, при різ

них зовнішніх умовах. Результати таких визначень одержу

ють з різною точністю, з різною мірою надійності; одні з

них будуть більш, інші ■— менш точними. Такі виміри, як

відомо, називаються нерівноточними.

Цілком очевидно, що при виводі остаточного значення з

ряду нерівноточних вимірів однієї і тієї ж величини ми не

можемо вже брати просте середнє арифметичне, тому що на

остаточний результат більш точний-вимір повинен мати біль

ший вплив. Інакше кажучи, при виводі остаточного значення

з ряду результатів нерівноточних вимірів необхідно брати

до уваги якість, надійність кожного окремого виміру.

Якість результату виміру, міру його на

дійності визначають числом, яке назива

ється його вагою. Якщо ми порівнюємо два або де

кілька результатів, то той з них, який буде найбільш точним,

повинен мати і найбільшу вагу, а менш точний — меншу

вагу.

Припустимо, що величина X визначалася п разів і одер

жано результати

Середні квадратичні помилки можуть служити критерієм

для визначення надійності окремих значень величини X. Чим

менша середня квадратична помилка пц, тим надійнішим бу

де результат %і. Через те за міру надійності його можна бу

ло б прийняти яку-небудь величину, обернено пропорціональ-

ну середній квадратичній помилці т г. Але ще більш чутли

вою мірою надійності окремого визначення величини' X буде

його вага. Так називається величина, обернено пропорщіо-

нальна квадрату середньої квадратичної помилки окремого

результату, а саме

де X — коефіцієнт пропорциональность Величина X може на

бирати різних довільних, але обов’язково однакових значень

при порівнянні в даній задачі однорідних величин різної

якості. Як правило, її вибирають так, щоб ваги рі, р2, ..., рп ви 

ражалися цілими двозначними або тризначними числами.

При визначенні ваг повинні задовольнятись дві умови:

1) середні квадратичні помилки тіг по яких обчислюються

ваги р і, повинні бути визначені досить надійно, тобто з дос

татньої кількості вимірів; 2) виміри, по яких визначають се

редні квадратичні помилки, а потім і ваги, повніші бути

вільними від систематичних помилок.

Приклад. Деякуй кут вимірявся два рази і одержано ре

зультати aL і а.,, середні квадратичні помилки яких нехай

будуть ті — ±5" і пі2 = -±ІО" відповідно. Знайдемо ваги

цих результатів.

Згідно з визначенням ваги

•*-1> -^ 2> • • - > Хц

з середніми квадратичними помилками

• ти т2, ..., тп.

\ \ х

(29,1)

Р1 т Ь Рі=* £ї, •••> Рп т^2 ,

X X

Рі (5»}2> Рі (

(іб"У2*

або

Р1 ’ 25 ’ Рг “ 100'

Припускаючи, що X ==' 1, одержимо А = 25’ ^2=Тбо; ПРИ

X = 100 будемо мати:/71 = 4, 1.

. Знайдемо тепер відношення ваг. Як легко помітити, при

першому і другому значеннях коефіцієнта пропорціональності

X воно буде однакове:

Рі '■ Р2 ~ : = ~г, (29,2)

тому що воно не залежить від коефіцієнта X.

Таким чином, при різних значеннях коефіцієнта X одер

жують і різні числові значення ваг, але співвідношення між

ними при цьому залишається незмінним (у нашому прикла-

ДІ 4:1).

Звідси випливає таке правило: ваги результатів

вимірів однієї або декількох однорідних

величин можна збільшувати або зменшу

вати в одне і те ж число разів, що, очевид

но, рівносильне зміненню коефіцієнта X.

Взагалі необхідно зауважити, що вага будь-якої величини

сама по собі ще ні про що не говорить. Ваги мають значення

лише при зіставленні або порівнянні між собою з точки зору

точності, надійності результатів визначень однієї або декіль

кох однорідних величин. Співвідношення між вагами ніби по

казує, у скільки разів одна величина більш або менш надій

на від другої. Отже, поняття ваги є відносне, а величина ва

ги цілком залежить від значення коефіцієнта X.

Формула (29,2) має дуже важливе практичне значення

через те, що вона дає можливість за трьома будь-якими ве

личинами, що входять у цю формулу, знаходити четверту.

Розв’яжемо, налриклад, таку важливу задачу. Маємо ре

зультат виміру величини х з вагою рх і з середньою квадра

тичною 'Помилкою т.х. Знайти середню квадратичну помилку

виміру, вага якого р = 1.

Позначимо середню квадратичну помилку такого виміру

через [і.. Для її визначення напишемо основне співвідношен

ня (29,2) між вагами рх і р = 1 і відповідними їм середніми

квадратичними помилками тх та (і:

pJL = ^L

1 т 2'

звідки

= (29,3)

або

1^ = ±т х Урх, (29,4)

тобто середня квадратична помилка ц, що

відповідає виміру з вагою р — 1, буде в