Бугай П.Т. Теорія помилок і спосіб найменших квадратів

Подождите немного. Документ загружается.

•} трикутника BCD:

CD = £ C sin'‘‘. (b)

sin VI

Замінивши в (b) довжину сторони ВС її значенням (а),

будемо мати:

г . п Sin I sin III /-7П 1 Ч

f--=CD = AB . ... . (70,1)

' sin IV sin VI v > /

Цю функцію називають ваговою. Приведемо її до 'просто

го лінійного виду. Для цього замінимо 'найімовірніші значен

ня кутів виміряними значеннями і поправками до них, піс

ля чого прологарифмуемо:

r n _ ,„ s i n ( l + ( l ) } s m { 3 + (3) }

sin{ 4 -H 4)}sm {6-|-(fy }'

lg CD = \gAB-\ lg sin {1 -!-(l)}+lg£in (3-}-(3)} — lg sin (4+(4)}

— Igsin{6-t-(0)>.

Розклавши lg sin{ } в ряди Тейлора за формулою (69,13),

одержимо:

/= 1 ё С1) = 1ё Л 5 + ^ ^ + А (1 ) + ^ (3 ) -

Введемо такі позначення:

A l _ 1 _ 1 1 ^ 6 _ ) / Т А C)\

JQ7 ” 1’ ] (JT A 3l 107 = 4’ 107 6‘ ' >“ >

Після підстановки їх в попереднє рівняння одержимо ва

гову функцію в такому лінійному виді відносно поправок:

/ - lg С75- lg ^ в +Хх( 1 )+Х,(3)—Х4(4)- Хв(6). (70,3)

Цей вираз цілком подібний до формули (68,4). Величини

X називаються ваговими коефіцієнтами. Як видно з позна

чень (70,2), вони в нашому прикладі дорівнюють змінам ло

гарифмів синусів кутів при зміні кутів на І" і виражені в

одиницях сьомого знака логарифмів.

Якщо при розв’язуванні нормальних рівнянь корелат в

схему введемо додатковий стовпчик X, в який випишемо ве-

личини [аХ], [&Х], [сХ], [d\J, fXX] і будемо «ад ними прово

дити ті ж операції, що й над коефіцієнтами і вільними чле

нами нормальних рівнянь корелат, то в останньому рядку

стовпчика X одержимо величину

[XX.4]= р-. (70,4)

Якби коефіцієнти X,. вагової функції точно дорівнювали

частковим похідним lg CD, то [ХХ.4] дорівнювала б оберненій

величині ваги I g CD. Насправді ж коефіцієнти X,- ми взяли

збільшеними в 107 .раз, а тому

звідки

1 - - = У [а.х.4] f70 5)

у Pf 107 " ^ ^

Середню квадратичну помилку в логарифмі сторони знай

демо за формулою

ТП\£ C D = ± - ~ ^ . (70,6)

V pf

Ця помилка виражена в одиницях сьомого знака лога

рифмів.

Щоб знайти відносну помилку в довжині сторони CD, мір

куємо так. Припустимо, що вона дорівнює -jj. Тоді лінійна

її помилка буде де L — довжина сторони CD. Середня

■ квадратична помилка в логарифмі сторони CD, очевидно, до

рівнюватиме:

т 1исД = ± |/ ( ^ 1 п і ) 2( ^ ) 2= ± ^ (1 п І)4 ->

або

.ML м

t n ig c D = ± - ^ - • - j £ = (70,7)

де М — модуль переходу від натуральних логарифмів до

десяткових.

З другого боку, середня квадратична помилка в логариф

мі тієї ж сторони CD за формулою (70,6) дорівнюватиме:

ЯІ Iff CD — І

V Р

V-V ІА.Х.4]

107

(70,8)

ГІрирівінюючи праві частини рівностей (70,7) і (70,8). бу

демо мати:

— = »У tu -4i

N м І07

(70,9)

§ 71. ВРІВНОВАЖЕННЯ ГЕОДЕЗИЧНОГО ЧОТИРИКУТНИКА

(ЧИСЛОВИЙ ПРИКЛАД)

Виміряні кути

1. 2Г05'24",3 5. 43°38'47",8

2. 75 52 18,4 / 6. 53 18 57,2

3. 55 50 55,4 7. 54 49 25,8

4.27 11 20,3 8.28 12 51,4

Логарифм вихідної сторони АВ = 4.0020924. З цими да

ними необхідно врівноважити кути геодезичного чотирикут

ника і визначити відносну помилку в довжині сторони CD

(схему чотирикутника див. рис. 15). Усі обчислення прово

димо у відповідних схемах в такому порядку.

Таблиця 44

1. Складання умовних рівнянь трикутників

Номери

трикут

ників

, Назва

! ВерШИН

: Номери

кутів

Виміряні кути

Умовні рівняння поправок

трикутників

1 21° 05' 24",3

(1) + (2) + (3) + (4)—1",6 - 0

75 52 18,4

3 w 55 50 55,4

4 27 11 20,3

179 59 58,4

ге-,

-1 .6

28 12 51,4

43 38 47,8

53 18 57,2

54 49 25,8

(5) + (6) + (7) + (8) + 2", 2 - 0

180 00 02,2

+ 2,2

1 21 05 24,3

(1) + (2) + (7) + (8)—0", 1 " 0

28 12 51,4

75 52 18,4

III

54 49 25,8

179 59 59,9

w 3

—0,1

П р и м і т к а. Знак вільного члена умовного рівняння трикутників

визначається за правилом: «те, що є, мінус те, що повинно бути».

2. Складання полюсного умовного рівняння

Беремо полюс в точці В. Позначаємо промені, що вихо

дять з неї, через а, Ь, с і записуємо очевидну рівність

а Ь с _ і

Ь с ~ а ~

Замінивши відношення сторін відношеннями синусів про

тилежних їм кутів, будемо мати:

sin VII sin (IV+V) sin I ,

sin (I + VIII) sin VI sin IV

Приводимо це рівняння за формулою (69,15) до ліній

ного виду:

( Д і ~ Ді+8)(1) + (Д 4+5 —Д4) (4)-f-A 4+5 (5) — Дд (6)-}-

+ А 7 ( 7 ) -А 1+8(8 )+ ц ;4- 0 .

Номери

кутів

Чисельник

Номери

кутів

Знаменник

Виміряні

кути

lg синусів

кутів

Виміряні

кути

lg синусів

кутів

54°49'25",8

9.9124265

+ 14,9

1+8

49° 18' 15",7

9.8797746

+ 18,1

4 + 5

70 50 08,1

9.9752389

+ 7,3

6 53 18 57,2 9.9041426

+ 15,7

1 21 05 24,3 9.5561038 + 54,6

4 27 11 20,3

9.6598466

+ 41,0

9.4437692

ї, 9.4437638

= 4-54.

36,5 (1) —33,7 (4)-)-7,3(5) —15.7 (6) — 14,9 (7) —18,1 (8 )+ 5 4-0.

3. Складання вагової функції

Для оцінки точності результатів врівноваження знаходимо

середню квадратичну помилку в логарифмі сто,рони CD

(найбільш віддаленої від вихідної сторони А В). Для цього

складаємо вагову функцію. З трикутників ABC і ACD маємо:

А тИП + Ш) с о = АС —

С»П \/ ' С If

sin VIII

sin IV ’ sin(VI + VII) ’

звідки

£7 1 Ґ'ГЛ 1 л о sin (И + III) sin VIII

F=\gCD = \gAB sin ,v sin (vnrvr,j,

або

/?о+Хг(2)+Хї(3) - ^(4) -X e(6) - X7(7)+X8(8).

Таблиця 46

Обчислення коефіцієнтів вагової функції

Номери

кутів

Виміряні кути

Номери

кутів

Виміряні кути

2 + 3

131°43'13",8 -18,7 4

27°11'20",3

41,0

28 12 51,4 39,2 6 + 7

108 08 23,0

— 7,0

F « /'0- 18,7 (2) -18,7 (3) -41,0 (4)+7,0 (6)+7,0 (7)+39,2 (8).

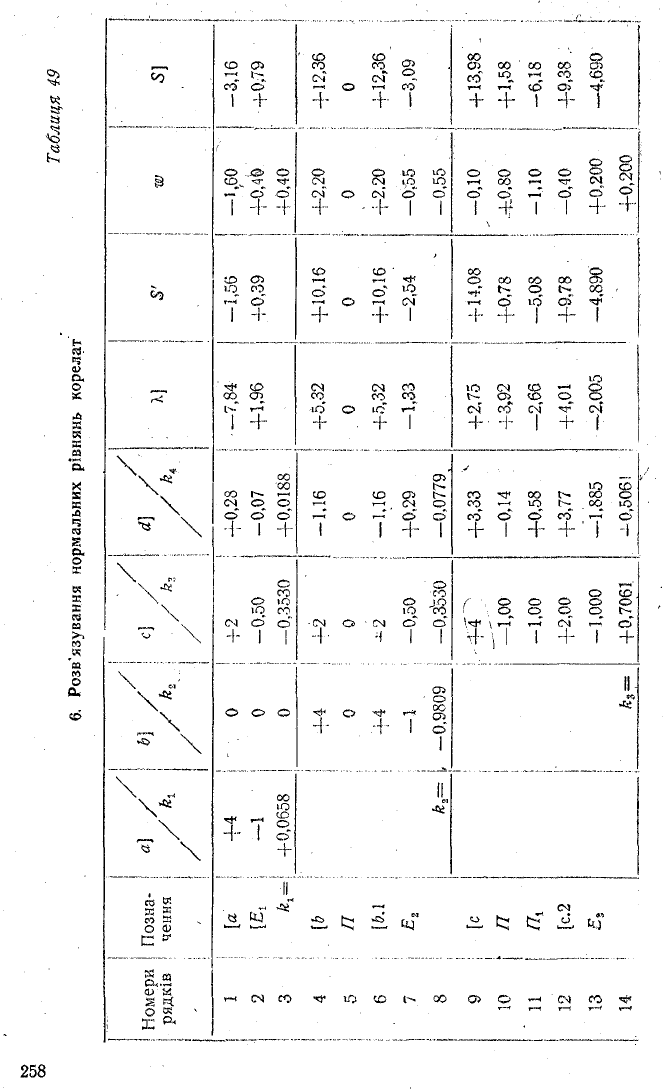
і. Розв'язування нормальних рівнянь корелат

со со

О)

00 со оо

Сч

см

СО

г-ч

СО

1—<

со

СО

а>

4 -

+ +

о о о

см 1.0

ю 1—1

оо чг

см'

о см

. +

о*

о~

со

rff

со

о"

т-н

7 °

-sH

СО см

см

со

со аз

со

I'-*'

t—^

о ю

Г“•

см

со

. +

+ +

СО <У> *"•

»-». сч о

0 ^ 0 0

І + І

_ со

О J O

Ю СО

' сч о о "

н І І

со

00 І'-

ю t—

О СО

+ +

О)

СО

сч

( ■■

00 о

О 0 0 СО 0 0 0 5

Ь» О Ь* 00

г-« о і о стГ ^

-і- + 1 + 1

о о

<N T-Z

+ І

со

ь-

4 - S

ос

іц

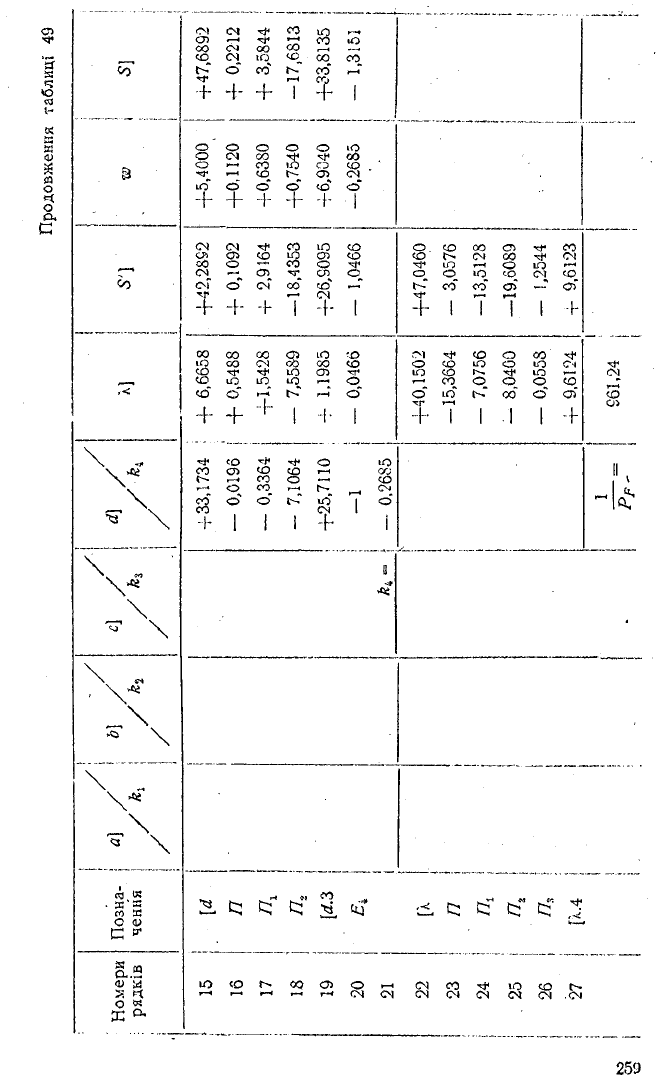
Номери

поправок

а b с,

d L

1 1

1 +3,65

+5,65

2 і 0 1

-1,87

: 0,13

0 0

-1,87

—0,87

0 0

—3,37

-4,10

—6,47

0 1

+0,73

0 +1,73

0 1

—1,57

+0,70

+0,13

7 0 1

• 1,19

+0,70

+4,19

0 1

-1,81

-f-3,92

+4,11

4 4 4

— 0,88

—2,52 +8,60

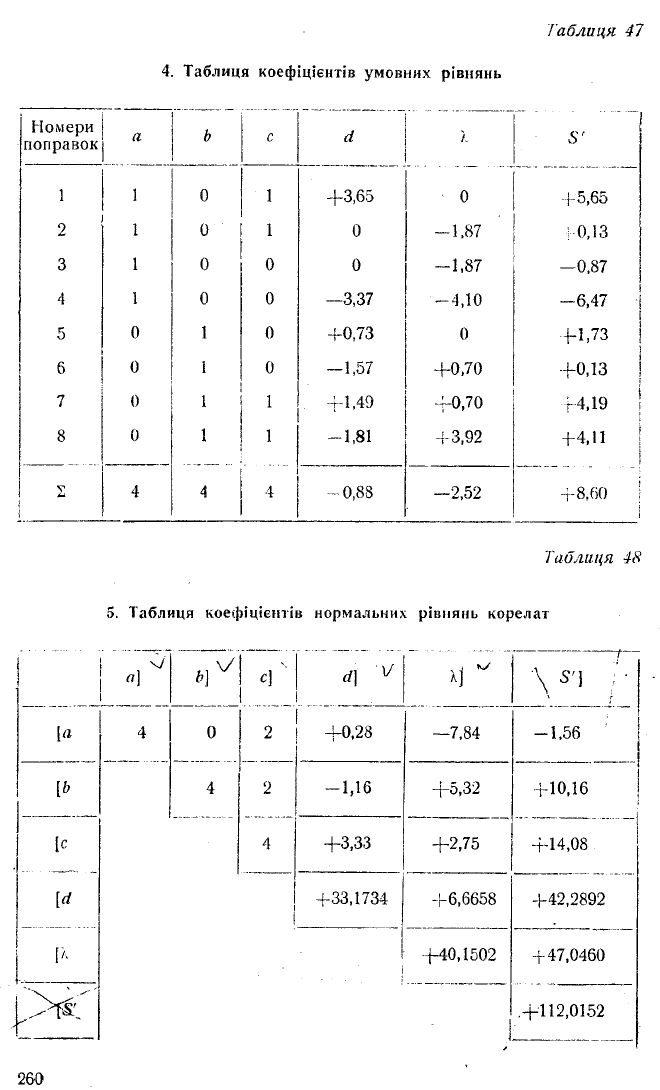
Таблиця 48

5. Таблиця коефіцієнтів нормальних рівнянь корелат

Т 7 '

с]

d\ v X] "

V ' 1 Г

+0,28

—7,84 — 1,56

-1,16

+5,32

+10,16

+3,33

+2,75

+14,08

+33,1734

+6,6658

+42,2892

+40,1502 + 47,0460

+112,0152

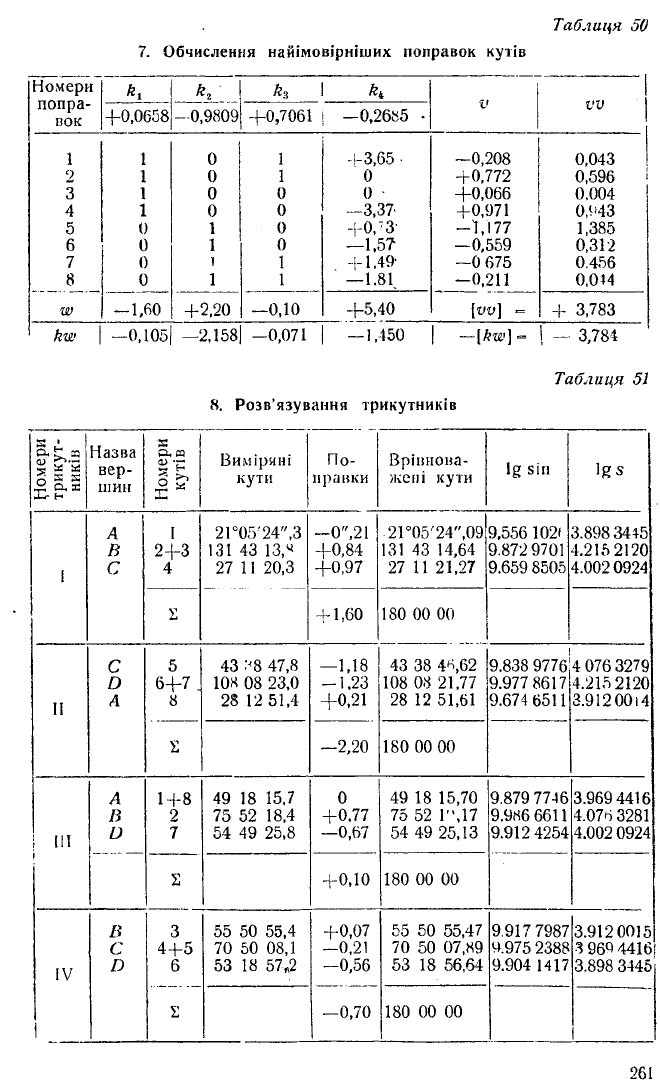
7. Обчислення найімовірніших поправок кутів

Номери

попра

вок

+0,0658

-0,9809

+0,7061

—0,2685 •

1 1 0

1 -1-3,65 ■

-0,208 0,043

1 0

1 0 +0,772

0,596

3 1

0 •

+0,066

0,004

0 —3,37'

+0,971

0,443

5 0

0 + 0,73' -1,177

1,385

0 —1,5? —0,559

0,312

1,49

- 0 675

0.456

8 0

1 1

— 1.81

-0,211

0,044

w -1,6 0

+2,20

—0,10 +5,40

[VV) =

+ 3,783

-0,105

—2,158 -0,071

— 1,450

—[kw] =

1 — 3,784

Таблиця 51

8. Розв’язування трикутників

Номери

трикут

ників

Назва

вер

шин

Номери

^ кутів

Виміряні

кути

По

правки

Врівнова

жені кути

lg Sill

lg s

2+3

2Г05'24",3

131 43 13,ч

27 11 20,3

—0",21

+0,84

+0,97

21°05'24",09

131 43 14,64

27 11 21,27

9,556 1021

9.8729701

9.6598505

3.898 3445

4.215 2120

4.0020924

+ 1,60 180 00 00

6+ 7

43 :^8 47,8

10Н 08 23,0

28 12 51,4

—1,18

-1,23

+0,21

43 38 46,62

108 08 21,77

28 12 51,61

9.838 9776

9.977 8617

9.674 6511

4 076 3279

4.215 2120

3.9120014

X —2/20 180 00 00

1 III

1+8

49 18 15,7

75 52 18,4

54 49 25,8

+0,77

—0,67

49 18 15,70

75 52 Г‘,17

54 49 25,13

9.879 7746

9.986 6611

9.912 4254

3.969 4416

4.076 3281

4.002 0924

2 +0,10 180 00 00

4+ 5

55 50 55,4

70 50 08,1

53 18 57*2

+0,07

—0,21

—0,56

—0,70

55 50 55,47

70 50 07,Н9

53 18 56,64

9.917 7987

4.975 2388

9.904 1417

3.9120015

3 964 4416

3.898 3445

180 00 00

9. Оцінка точності

Середня квадратична помилка одиниці ваги

Іі= ± у j ур_ = ± у 3J 83_ ± q „ 97

Середня квадратична помилка в логарифмі сторони CD

tn\g CD

~ * V -F 7 -

107‘

Відносна помилка в довжині сторони CD

1st

ЛГ МЛО1 ' 14и 000’

§ 72 ВРІВНОВАЖЕННЯ НІВЕЛІРНОЇ СІТКИ

(ЧИСЛОВИЙ ПРИКЛАД)

Врівноваження нерівноточних умовних вимірів розгляне

мо на прикладі врівноваження нівелірної сітки (рис. 16), яка

в §55 була вже врівноважена методом посередніх вимірів.

Рис. 16.

Нижче подаємо вісім виміряних різниць висот точок А, В,

С, D і Е в напрямах, показаних на рисунку стрілками, і дов

жини відповідних нівелірних ходів.

DA ... A j-+16,808 м,

Л3 = + 7,912 м,

/г3 = +-31,182 м,

Л4 =+14,894 м,

Л5 = + 14,384 м,

h6 = — 16,302 м,

/г7 = + 8,914 м,

/г8 = -+23,286 м,

АВ

ВС .

ЕА

ЕВ ,

й^ = 24,2 км,

d2 = 10,8 км,

d3 = 18,4 км,

dA = 14,9 км,

d6 = 21,2 км,

ds = 12,5 км,

d7 = 9,3 км,

ds= 7,1 км.