Бугай П.Т. Теорія помилок і спосіб найменших квадратів

Подождите немного. Документ загружается.

Якщо тепер підставимо (18,5) в (18,1), то одержимо по

милкове значення функції (18,3), яке позначимо через F':

, F>~F{x,y} = F { X i - (х), Y0-(y)}. (18,6

В геодезичній і астрономічній практиці всі виміри про

водяться,' як правило, ретельно і досить точними інстру

ментами, а тому результати вимірів х та у будуть мало

відрізнятися від істинних* значень аргументів X і Y. Крім

того, згідно з попередньою умовою, наближені значення Х0

і Y0 також досить близькі до них. Отже, можна вважати, що

(х) і (у) є величини малі. Внаслідок цього останній вираз

функції можна записати в “такому вигляді:

(18,7)'

Віднімаючи з (18,7) вираз (18,4), знайдемо істинну по

милку функції для даної пари виміряних значень аргумен

тів х та у:

^ F - F - F - (to),IW-WI+ ( § (18,8}

Віднімаючи же з (18,5) рівності (18,2), знайдемо істинні

помилки виміряних значень аргументів, які позначимо че

рез Дх і А у:

х - Х = ( Х ) - ( х ) - Ь х %

у - Y= (Y) — (y) = Ay.

Підставивши (18,9) в (18,8), знайдемо одне значення

істинної помилки функції, обчислене за даною парою виміря

них значень аргументів:

ЛМ § ) 0Д* + (!?)0ДУ- (18,10)

Для визначення квадрата середньої квадратичної по

милки функції (18,1) незалежних між собою аргументів не

обхідно знайти всі можливі її істинні помилки, загальний

вигляд яких дано виразом (18,10), піднести їх до квадрата,

підсумувати і поділити на число всіх можливих помилок

функції.

Припустимо, що аргумент X вимірявся k разів, a Y — п.

разів і одержано такі результати:

Xj, х2, ■ ■ ■, ,

Уі, У2, - • - , У»-

Якщо підставимо ці значення в (18,9), одержимо:

к х иЬх2,-■ ■ ,кхи ,

■ -ЛУп.

Це істинні помилки виміряних величин. Число .Можливих

сполучень по дві з цих помилок буде дорівнювати! &/г. Під

ставивши їх в (18,10), знайдемо kti значень помилок функ

ції. Таким чином, будемо мати: ■

Д Fn = а Д х1 + р Д уи Д F21 = я Д л:2 + р Д yl J

Д Fv2 = а \х 1 + рД у2, AF22 = aAx2 + р Ду],

ДFin = а Д х, + р Д уп , Д F2n = а Д ,v2 + р Д уп,

Д Fki = а Д Xft + р Aylt

Д^й2= а Д ^ +рд_у2, /1011ч

....................................... (lo.il)

д Ркп = лАхк + $Ауп.

Тут для скорочення записів введено позначення

О 0 = а’ & f)0 = P- (18,12)

Число таких груп рівнянь буде k по п рівнянь у кожній.

Піднесемо тепер ці kn істинних помилок функції до

квадрата і результати підсумуємо по групах:

[Д Fjj2] = п а2 Д xt2 + Pa [Ajr?\ t 2<хрДл;1 [ A_y(],

[Д F2?] = n а? Д Xj2 + p2 [Д y,-2] + 2а p Д x> [ Дy t],

ІД = « а2 Д a:32 + P2 [Д yil [ + 2a p Д x3 [Дyt],

[Д Fk?\ =tta2 Д JCft2 + p2 [Д y,-2] + 2a p [A_yf]

[Д/72] =/га2 [Дл;/] +^p2 [Д_у/2] +2 a p [Д xj\ [Дj/і[,

де ] = 1, 2, ..., k, /= 1, 2, ..., n.

Поділивши останню загальну суму квадратів помилок

функції на число помилок kn, одержимо:

[Д/72] ]А X/2] [Лу,г] Г Д Jt,1 [Д у.)

~2 ' + р2- + 2арі--./і -LZfL. (18,13)= a , -

ftrt ft Г n r ft

З огляду на четверту властивість випадкових помилок

Ах і Ду третій член в правій частині цього виразу при ве

ликій кількості вимірів аргументів х іу буде величина мала в

порівнянні з двома першими членами, а тому ним можна

знехтувати. Далі, величини

[А х/] [Л_уг2)

ft п

є квадрати середніх квадратичних помилок тгх і тгу аргу

ментів. Заміняючи позначення а і (J частковими похідними

функції, одержимо остаточну формулу:

Легко можна вивести подібну формулу і для функції

трьох і більше аргументів. Вона матиме такий загальний

вигляд:

тобто квадрат середньої квадратичної помилки

функції незалежних величин дорівнює сумі

добутків квадратів часткових похідних функ

ції по кожному аргументу на квадрати серед-

ніх квадратичних помилок відповідних аргу

ментів.

При застосуванні формули (18,14) необхідно мати на

увазі таке:

1) аргументи, які входять під знак функції, повинні бути

незалежними між собою;

2) середні квадратичні помилки тх, ту, •••, іпи повинні

бути відомі і величини їх визначені із спеціальних дослі

джень. Крім того, результати вимірів аргументів неповинні

містити систематичних помилок; тільки при цій умові ми

мали право в формулі (18,13) нехтувати членом

§ 19. ОКРЕМІ ВИПАДКИ ОЦІНКИ ТОЧНОСТІ ФУНКЦІЙ

Застосуємо формулу (18,14) до найпростіших функцій,

оцінку точності яких досить часто доводиться давати на

практиці.

1. Дано функцію f=kx, де к -- сталий коефіцієнт і

піх — середня квадратична помилка величини л; знайти /И/.

Знаходимо спочатку похідну

Підставивши її в формулу (18,14), одержимо:

(dF \ з I dF у- , (d F y-

mҐ = Ы 0 m* + Ы „ m>' + ■ • ■ + Ы )0 m'c' (18,14)

пі/2 = k-inx2, або ш, = ±kmx.

(19,1)

Отже, середня квадратична помилка добутку

точного сталого числа на аргумент, значення

якого одержано з вимірів, дорівнює добутку

сталого точного числа на середню квадра

тичну помилку аргумента.

2. Дано функції fi=x+ y, або / 2 = х —у і середні квадра

тичні помилки тх та ту аргументів; знайти mf.

Часткові похідні для першої функції будуть:

^ - + 1

дх ' ’ ду ^

і відповідно для другої функції

^ - 4 1

____

дх ду ■

Застосувавши (18,14), матимемо:

/Пд 2 = тх 2 + ту.

m,f = trix2 + ту.

Звідси

mft = mft ^ ± у mJi + mT (19,2)

Таким чином, середня квадратична помилка

суми або різниці двох аргументів різної

точності дорівнює квадратному кореню із

суми квадратів середніх квадратичних по

милок аргументів.

У тому випадку, коли аргументи х і у виміряні з одна

ковою точністю, тобто тх = ту = т,

то m.f <= ±m \f2] (19,3)

3. Дано лінійну функцію

f — + Ul Х1 + й2 Х'д І • • • І &п Хп ,

де хи х2, . . ■ , х„ — незалежні між собою аргументи,

яь а2, ..., ап — сталі коефіцієнти, а також середні квадратич

ні помилки аргументів тХі, тХг, ... , тХп• Знайти середню

квадратичну помилку функції mf .

Маємо

df _i_„ df 4-п df А-п

Ш Г ±аи Ш Г ±а2’ ■ дГп=±ап-

Застосувавши формулу (18,14), одержимо;

mf = ± Y а^тх^ + а2гШхг2 + ... Л-а^глх*. (19,4)

Якщо ВСІ аргументи будуть рІВНОТОЧНІ, тобто OT.Vl = Отл, =

= ... =тхп = т, тоді

nif = + m Y аг2 + а22 + ... + ал2 = ±_m\f\al\. (19,5)

4. Знайдемо тепер дуже важливу формулу для визна

чення середньої квадратичної помилки М середнього ариф

метичного з результатів рівноточних вимірів однієї величини.

Середнє арифметичне обчислюється за такою формулою:

X і "Ь X<t -І- . . . -b Хп 1 1 1

/ = * „ = — „-----------" = '!' п Х і + • • • + -пх -

Отже, воно буде лінійною функцією результатів окремих

рівноточних вимірів. Диференціюючи цю функцію, знаходимо:

K . = VL= =

dxt дх., ' ' ' дхп п '

Застосувавши (18,14), матимемо:

Щ = /И= ± у ( 1 ) W + ( і fmx 2+ ... + ( і )1тХп\

Беручи до уваги, що всі виміри проведені з однаковою

точністю т, попередній вираз можна записати так:

М = ±

або

М-±-£=, (19,6)

у п

тобто середня квадратична помилка середньо

го арифметичного з рівноточних вимірів до

рівнює середній квадратичній помилці одного

виміру т, поділеній на квадратний корінь з

числа вимірів.

Формула (19,6) показує, в якій мірі послабшав вплив

випадкових помилок на остаточний результат внаслідок бага

тьох вимірів, а саме вона показує, що середня квад

ратична помилка середнього арифметичного

М в Уп разів менша від середньої квадратич

ної помилки т одного виміру. На основі цього

можна було б зробити висновок, що для того, щоб одер

жати остаточний результат багатьох вимірів однієї величини

з дуже малою помилкою М, треба провести дуже велику

’кількість вимірів. Але, як це ми зараз покажемо, практично

робити це недоцільно. Щоб переконатись в цьому, знайдемо,

як. змінюється величина М в залежності від збільшення

кількості вимірів п.

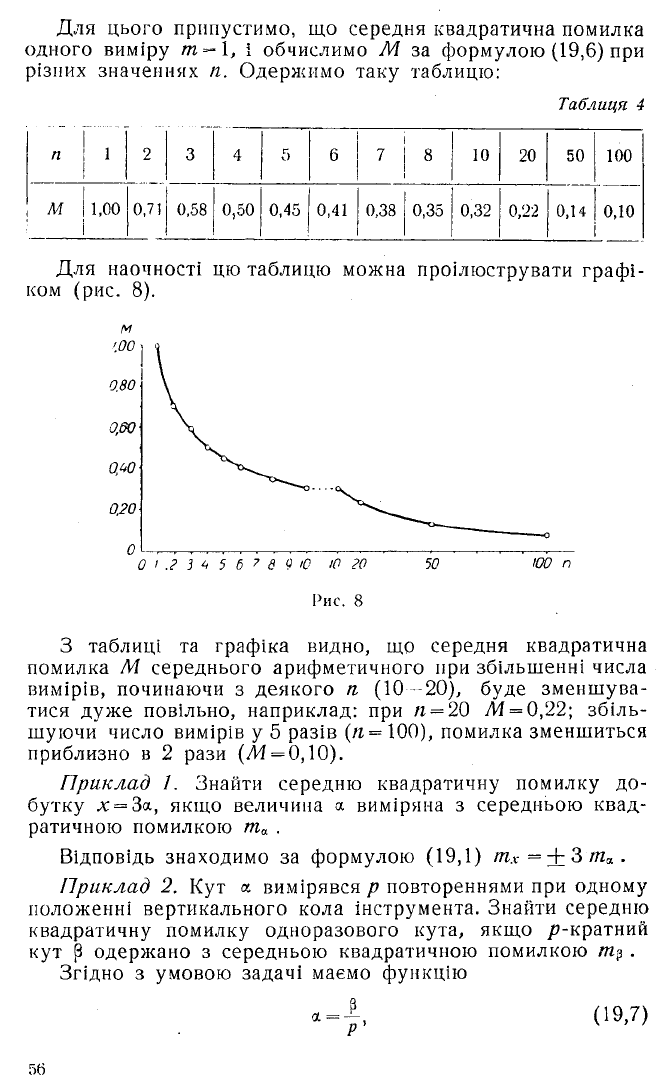
Для цього припустимо, що середня квадратична помилка

одного виміру т=-\, і обчислимо М за формулою (19,6) при

різних значеннях п. Одержимо таку таблицю:

Таблиця 4

4 5 6 7 8 10

20 50

100

1,00

0,71

0,58 0,50 0,45 0,41

0,38 0,35 0,32

0,22 0,14

0,10

Для наочності цю таблицю можна проілюструвати графі

ком (рис. 8).

Рис. 8

З таблиці та графіка видно, що середня квадратична

помилка М середнього арифметичного при збільшенні числа

вимірів, починаючи з деякого п (10—20), буде зменшува

тися дуже повільно, наприклад: при п = 20 УЙ = 0,22; збіль

шуючи число вимірів у 5 разів (п = 100), помилка зменшиться

приблизно в 2 рази (УИ = 0 ,10).

Приклад І. Знайти середню квадратичну помилку до

бутку х = 3а, якщо величина а виміряна з середньою квад

ратичною помилкою та .

Відповідь знаходимо за формулою (19,1) тх = + 3 тЛ .

Приклад 2. Кут а вимірявся р повтореннями при одному

положенні вертикального кола інструмента. Знайти середню

квадратичну помилку одноразового кута, якщо /ькратний

кут р одержано з середньою квадратичною помилкою .

Згідно з умовою задачі маємо функцію

середня квадратична помилка якої та дорівнюватиме:

та = ± ”± . (19,8)

Приклад 3. Величину кута А одержано як суму двох

інших кутів В і С. Знайти середню квадратичну помилку

тА кута А, якщо середні квадратичні помилки кутів В і С

дорівнюють відповідно т в= ±3" і «с = + 5".

За формулою (19,2) знаходимо:

тА = ± уіпп'Л~тг = ± y ^ T f + ^ f ~ ± 6".

Очевидно, що якби кут А був знайдений як різниця

кутів В і С, то його середня квадратична помилка була б

такою ж самою.

Приклад 4. Кути в трикутнику вимірялися однаково

точно з середньою квадратичною помилкою тЛ = ±2". Знайти

середню квадратичну помилку суми кутів трикутника. ,

За формулою (19,5) маємо:

ті = + У т а2 + та2 + та2^ ±та | / 3 ^3",5. (19,9)

Приклад 5. Віддаль визначається далекоміром за фор

мулою d = kl + c, де Іг— коефіцієнт далекоміра, а с - стала

далекоміра, які вважаються безпомилковими. Визначити се

редню квадратичну помилку та віддалі, якщо величина І

визначається як різниця 1 = 1' — Г двох відліків по далеко-

мірній латі по крайніх нитках сітки зорової труби і середні

квадратичні помилки відліків т' = т" = 0,5 см..

Спочатку знаходимо середню квадратичну помилку ті різ

ниці відліків:

ті = ± т у 2 = +0,7 см.

Звідси середня квадратична помилка віддалі

та = + knii = + 0,7 k.

При k = 100

md =0,7 м.

§ 20. ОБЧИСЛЕННЯ СЕРЕДНЬОЇ КВАДРАТИЧНОЇ ПОМИЛКИ

ЗА НАЙІМОВІРНІШИМИ ПОМИЛКАМИ

При визначенні середньої квадратичної помилки одного ви

міру з ряду результатів рівноточних повторних вимірів однієї

величини ми припускали, що нам^відоме істинне її значення X.

Далі ми знаходили істинні помилки А окремих вимірів і по

них виводили формулу (16,5). Але, якщо нам буде відоме

істинне значення відшукуваної величини, то зовсім немає

потреби її вимірювати, а через те й взагалі говорити про

точність вимірів. Формула (16,5) має застосування лише в

тих порівняно небагатьох випадках, коли з теоретичних

міркувань нам відомо істинне значення деякої функції вимірю

ваних величин. Так, можна говорити про середні квадратичні

помилки виміряних суми кутів одного трикутника, суми ку

тів зімкнутого полігона або суми перевищень зімкнутого

нівелірного полігона і т. д. В більшості ж випадків істинні

значення вимірюваних об’єктів (довжини ліній, величини

кутів, перевищень між двома точками та ін.) нам невідомі.

В завдання спостерігача входить визначити найбільш надій

ні, найімовірніші остаточні значення таких величин з бага

тьох повторних вимірів і оцінити їх точність.

Нехай маємо результати рівноточних вимірів однієї і тієї

ж величини

Не знаючи істинного значення X, ми, згідно з принципом

арифметичної середини, за найімовірніше значення відшу

куваної величини приймаємо середнє арифметичне Х0. Ре

зультати окремих вимірів будуть відрізнятися від нього на

величини

Величини 8,- відрізнятимуться ВІД ІСТИННИХ ПОМИЛОК А і тим

менше, чим менше середнє арифметичне Х0 відрізнятиметься

від істинного значення X. Подібно до того, як ми назвали

середнє арифметичне найімовірнішим значенням вимірюваної

величини, так і величини 3/ називають найімовірніши

ми, або залишковими помилками окремих резуль

татів вимірів.

Щоб уникнути надалі непорозумінь, необхідно чітко ро

зуміти ту різницю, яка існує між відхиленнями vu v2,

. . . , vn результатів окремих вимірів аи а.,, . . . , ап від се

реднього арифметичного з них (§ 15) та найімовірнішими

помилками 8,, 8,, ..., 8„ . Перші з них ми домовились об

числяти за формулою

# 1, йо> • • • і а п •

(20,1)

&П X q — о п .

V і

X q d t ,

(а)

а другі — за формулою

Звідси

Vi=—hi. (в)

Якщо рівності (а) і (б) записати так:

+Т' (20,2)

а о — а і о;,

то легко помітити, що відхилення означають ті поправки,

які треба додати до результатів вимірів, а найімовірніші

помилки — ті помилки, які треба відняти від них, щоб і в

першому і в другому випадках одержати найімовірніше

значення Хп. Надалі при викладанні курсу ми постійно бу

демо додержуватись такої термінології.

Не знаючи істинних помилок Д результатів окремих ви

мірів, для оцінки точності використовуватимемо найімовір

ніші помилки 8 в такий спосіб.

Напишемо два ряди рівносте’!:

у\г = Д1, я, А0 = Зь

а3—Л"=-Д2, ^203) а,-Х ^Ь .г,

а , г X

— Д/7,

a n X q

—

о„

Віднімаючи почленно від перших рівностей другі, одер

жимо:

^ 0- А ’ = Д1- 81,

Х0- Х = А2-5 2,

Х0- Х = Ап-о п.

Стала різниця Х0—Х означає істинну помилку серед

нього арифметичного Х0. Раніш ми позначали її через Д„.

Отже, рівності (20,5) можна записати так:

Aj = 3j + Д0,

Д2 = 52 + До> (20)6)

Дл = 0/1 + До-

Піднесемо їх до квадрата і результати підсумуємо:

]ДД] = [88]+/гД02 + 2Д0[8]. (20,7)

Ллє легко довести, що [8] = 0. Справді, знайдемо суму

рінпостей (20,1):

[а] — п Х0 = [3|.

Підставивши замість Х0 його значення:

и п ’

одержимо

[S]- о , (20,8)

тобто сума найімовірніших помилок результа

тів рівноточних вимірів завжди дорівнює ну

лю.

Таким чином, рівняння (20,7) набирає такого вигляду:

[ДД] = [S8J + я Др2. (20,9)

Всі члени в правій частині цієї рівності є величини

додатні. Звідси випливає така важлива властивість найімо

вірніших помилок:

[ДД] > [88], (20,10)

тобто сума квадратів найімовірніших помилок

завжди менша від суми квадратів істинних

помилок. Це вірно при будь-якій системі значень істин

них помилок Д.

Використаємо тепер співвідношення (20,9) для виведення

формули, за якою визначається середня квадратична помил

ка одного виміру за найімовірнішими помилками 8. Для цього

поділимо це співвідношення на число вимірів и:

або

Беручи до уваги, що

[ДА ]_{Щ 2

п ~ п '

т 2 = Ц^ + Д0а. (20,11)

А [Д] Д1 + Д2+---+ДЯ

можемо записати:

Д„а =

2 І [Д] \2 [А2] 2(Д(Д2 + AtA3+ ... + Д ^,,+ ... + Ал)

0 j JT1

Добутки Д,Д2, Д^з, ..., Дл- іДп мають усі властивості

випадкових помилок. Отже, при досить великому числі ви

мірів сума їх буде величиною малою, а тому другим чле

ном в останній рівності можна знехтувати. Тоді