Бугай П.Т. Теорія помилок і спосіб найменших квадратів

Подождите немного. Документ загружается.

Різниця U—L0 буде величиною сталою. Позначимо її

через w. Тоді

8^ = vl -f ш,

82=®2+ “ . (15,П)

Зл = 1>п + w-

Піднесемо ці рівності до квадрата і результати підсу

муємо:

[82] =

Але, згідно з (15,5), [о] =0. Отже,

[82] = [г>2]+лш8, (15,12)

Всі члени цієї формули є величини додатні, а тому

[З3] Ж 2]. (15,13)

Звідси випливає така друга математична властивість се

реднього арифметичного: сума [и2] квадратів від

хилень даного ряду величин /ь /2, . . ., Іп від

їх середнього арифметичного L0 завжди

буде менша від суми [ о2 j квадратів від

хилень цих величин від будь-якого довіль

но г о ч и с л a L'.

Ця властивість набирає для теорії помилок дуже важли

вого значення, якщо величини /ь /2, з яких визнача

ється середнє арифметичне, будуть не довільними числами,

а результатами вимірів однієї величини. Тоді відхилення

Уі, V2, • • •, Vn означатимуть ті поправки, які треба додати

до результатів вимірів, щоб одержати, згідно з принципом

арифметичної середини, найбільш надійне, або найімовірні

ше остаточне значення L0 вимірюваної величини. Сума квад

ратів їх буде мінімальна, що узгоджується з принципом най

менших квадратів, який лежить в основі теорії помилок.

На практиці при обчисленні середнього арифметичного до

цільно застосовувати такий спосіб.

Нехай , маємо результати рівноточних вимірів однієї ве

личини:

її, ^2> • • • > •

Візьмемо деяке довільне, але близьке до істинного набли

жене значення /о вимірюваної величини і знайдемо різниці

:іп правилом: «виміряне значення мінус наближене»:

Л k = єі>(

l->-h = z 2. (15,14)

..................... V

Іп А) ™ *

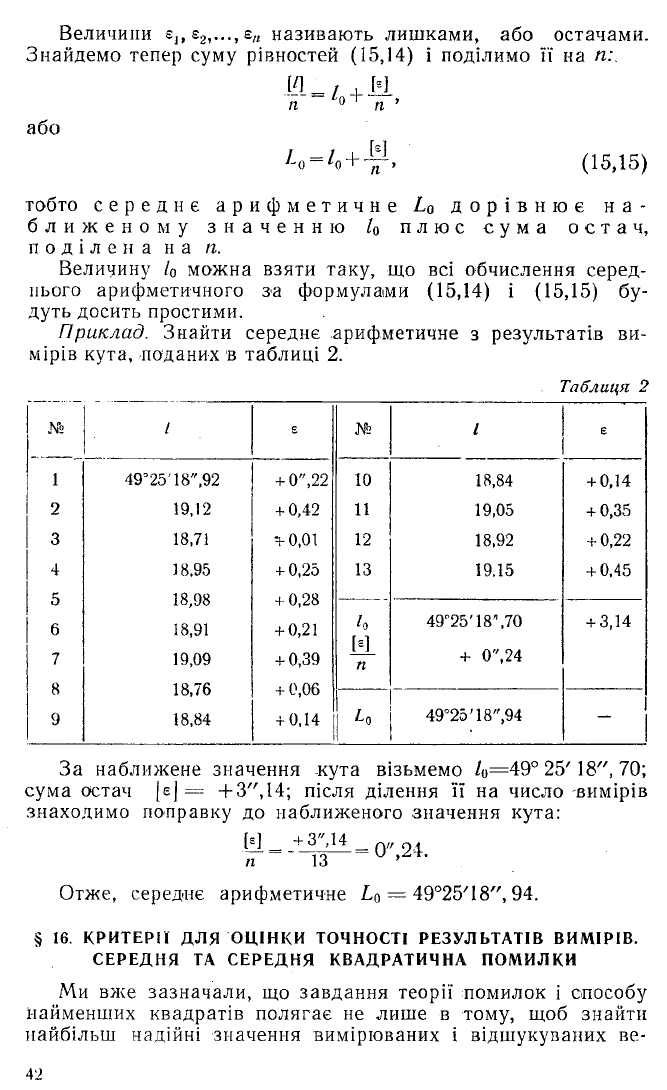
Величини в), в2,..., є„ називають лишками, або остачами.

Знайдемо тепер суму рівностей (15,14) і поділимо її на п:.

або

^0 = ^ + “ . (15,15)

тобто середнє арифметичне L0 дорівнює на

ближеному значенню /о плюс сума остач,

поділена на п.

Величину /0 можна взяти таку, що всі обчислення серед

нього арифметичного за формулами (15,14) і (15,15) бу

дуть досить простими.

Приклад. Знайти середнє арифметичне з результатів ви

мірів кута, поданих в таблиці 2.

Таблиця 2

№

в №

49°25'18",92 + 0",22 10

18,84

+ 0,14

2 19,12

+ 0,42 11

19,05 + 0,35

3 18,71

*+0,01 12

18,92

+ 0,22

18,95 + 0,25 13

19,15 + 0,45

18,98

+ 0,28

-------

18,91

+ 0,21

Грі

49"25'18л ,70 + 3,14

19,09

+ 0,39

[£1

+ 0",24

18,76 + 0,06

—

----------------

---

----------

18,84 + 0,14

Lt)

49°25'18",94

За наближене значення кута візьмемо /0=49° 25'18", 70;

сума остач (є) = + 3",14; після ділення її на число -вимірів

знаходимо поправку до наближеного значення кута:

Отже, середнє арифметичне L0 = 49°25/18", 94.

§ 16. КРИТЕРІЇ ДЛЯ ОЦІНКИ ТОЧНОСТІ РЕЗУЛЬТАТІВ ВИМІРІВ.

СЕРЕДНЯ ТА СЕРЕДНЯ КВАДРАТИЧНА ПОМИЛКИ

Ми вже зазначали, що завдання теорії помилок і способу

найменших квадратів полягає не лише в тому, щоб знайти

найбільш надійні значення вимірюваних і відшукуваних ве-

личин, а й в тому, щоб дати оцінку точності як результатів

безпосередніх вимірів, так і результатів їх обробки. Для цьо

го необхідно встановити, по-перше, на основі яких даних

можна дати цю оцінку і, по-друге, які способи або критерії

для цього будуть найкращими.

Якщо ми проведемо лише один вимір якої-небудь вели

чини і одержимо результат аі з відомою істинною помилкою

Дь то ми ще не матимемо достатньої кількості даних, щоб

судити як про точність, так і про умови виміру, тому що

характеристику точності ми не можемо базувати на випадко

вому значенні лише однієї помилки. Так, наприклад, помил

ку в 5" у значенні виміряного кута ми можемо одержати

при сприятливих умовах одномінутним теодолітом. Але така

помилка може з’явитися і при вимірі досить точним інстру

ментом (п’ятисекундним або двосекундним). Таким чином,

для оцінки точності і характеристики умов вимірів необхід

но мати ряд вимірів.

Якщо нам будуть відомі результати достатньої кількості

рівноточних вимірів деякої величини і істинні значення по

милок цих вимірів, то, аналізуючи їх, можна виявити і від

кинути грубі, а в деяких випадках і систематичні помилки.

Після цього ми одержимо ряд випадкових істинних помилок

Др д2, ..., Д„, (16,1)

па основі яких уже можна дати оцінку точності.

Кожна з помилок ряду (16,1) визначає точність відповід

ного їй виміру. Але жодна з них не може, про що ми тільки

що говорили, характеризувати точність усього ряду вимірів

у цілому. Для цього, очевидно, необхідно використати всі

помилки (16,1), причому ця характеристика повинна бути

єдиною для всіх окремих рівноточних вимірів однієї величи

ни і характеризувати всю сукупність умов вимірів, а саме:

точність інструмента, метод вимірів, зовнішні умови, май

стерність і досвідченість спостерігача та ін.

Припустимо, що ми маємо результати

^1 J ^2 У • * * > » /1 £ Г)\

а.", ап" ’

двох рядів вимірів однієї або різних, але однорідних вели

чин, наприклад кутів, проведених при різних умовах. Нехай

істинні випадкові помилки цих результатів будуть відпо

відно

А ' Д ' Д '

4 ; / 4 і

..............

д \ ; н а д

Л1 » а 2 » * • • > а л *

'Порівнюючи два ряди вимірів (16,2) з точки зору їх

точності, треба, очевидно, вважати точнішим той з них, у

якому результати менше відрізняються один від одного, і,

навпаки, чим більше вони будуть відрізнятися між собою,

тим менш точними слід вважати виміри. Отже, судити про

точність результатів вимірів необхідно по мірі їх розсіюван

ня, або дисперсії: чим більша дисперсія ряду, тим менша

ного точність.

Залежно від того, яка величина (приймається за міру

розсіювання результатів вимірів, існують такі критерії для

оцінки точності: середнє з абсолютних значень помилок, се

редня квадратична та імовірна помилки.

Середнім з абсолютних значень поми

лок називається середнє арифметичне з

абсолютних значень помилок результатів

рівноточнихвимірів.

Позначаючи його через 0, згідно з визначенням будемо

м ати:

e-U A U . (16,4)

Середньою квадратичною помилкою, яку

прийнято позначати через т, називаєть

ся квадратний корінь із суми квадратів

істинних випадкових помилок, поділеної

н а їх число, тобто

т = 4;

або в позначеннях Гаусса:

т^ + у Ш . (16,5)

Середня квадратична помилка, так само як і інші кри

терії оцінки точності, завжди повинна мати' подвійний знак ±.

Це значить, що величина А, точність якої характеризуєть

ся, наприклад, середньою 'квадратичною помилкою т, з од

наковою можливістю може мати помилку як -\-т, так і — т.

Умовно це записується так:

А ± т. (16,6)

Як видно з формул (16,4) і (16,5), обчислення серед

ньої помилки 0 значно простіше, ніж обчислення середньої

квадратичної помилки т. Однак середня квадратична помил

ка є найкращим критерієм для оцінки точності вимірів, то

му що вона має такі переваги в порівнянні з середньою та

імовірною помилками (про останню мова буде в § 17):

1) Середня квадратична помилка є досить чутливою мі

рою точності через те, що на її величину сильніше впливають

великі р,одо абсолютної величини випадкові помилки, які в

основному і визначають ступінь надійності результатів ви

мірів.

2) .Середня квадратична .помилка вже при деякому від

носно це дуже великому числі вимірів п набуває сталого

значення і .при дальшому збільшенні п змінюється дуже по

вільно. Так, наприклад, досить провести 10—20 вимірів, щоб

визначити т з точністю 0,3—0,2 її величини, що доводиться

в теорії імовірностей.

3) За величиною середньої квадратичної помилки можна

знайти так звану граничну помилку. Граничною по

милкою називається таке найбільше щодо абсолютної ве

личини значення випадкової помилки, яке ще може з’явитися

при даних умовах вимірів. Помилки, більші від граничної,

вже слід вважати грубими. Гранична помилка позначається

через Дгран. В теорії імовірностей доводиться, що при 100 ви

мірах більші від т випадкові помилки можуть з’явитися

приблизно в 32 випадках, більші від 2т — в 5 випадках і,

нарешті, більші від 3т при 1000 вимірах — лише в 3 ви

падках. Отже, появу такої випадкової помилки при 1000

вимірах можна практично вважати майже неможливою. Че

рез те. потрійну середню квадратичну помилку і приймають

за граничну1:

4) Дуже важливою властивістю середньої квадратичної

помилки т є те, що закони нагромадження .випадкових по

милок виражаються через т досить простими формулами,

тобто, як це буде показано далі, легко визначити середню

квадратичну помилку будь-якої функції безпосередньо вимі

ряних аргументів, якщо будуть відомі їх середні квадратич

ні помилки.

Для порівняння критеріїв оцінки точності т і 0 розгля

немо такий приклад. Візьмемо результати двох рядів вимі

рів, істинні помилки яких відповідно мають такі значення:

Знайдемо спочатку алгебраїчні суми помилок у цих двох

рядах:

і Сучасні інструкції приписують за граничну помилку приймати

Ліран = 2т. Це пояснюється тим, що, по-перше, імовірність, появи по

милки, більшої від Я т, відносно мала (не більша 1/20) і, по-друге, цим

самим встановлюються більш підвищені вимоги щодо точності геодезич

них вимірів.

(16,7)

1 ряд: - 2", 0", + 8", + 10", — 15", — 1".

2 ряд: —5", -1- 7",—6", + 4", + 7", — 7".

(16,8)

[Л]і-0, [А]2 = 0.

Звідси .виходить, що й середні значення помилок дорівню

ватимуть нулю. Це означає, що випадкові помилки даних

двох рядів вимірів задовольняють четверту властивістьівнпад-

кових ПОМИЛОК. І

Середні з абсолютних значень помилок будуть тут одна

кові:

М Ь ^ З б ! = б„

г п 6

Таким чином, за цим критерієм два дані ряди вимірів ма

ють однакову точність.

Знайдемо, нарешті, середні квадратичні помилки за фор

мулою (16,5):

ml-± j/ | 4 = 8",!,

/п 2- = ± |Л - | 4 - 6 " , 1.

Звідси видно, що другий ряд вимірів є точніший від пер

шого. До цього висновку можна було прийти вже з поперед

нього аналізу рядів помилок (16,8). Справді, в першому

ряді помилки за своєю абсолютною величиною змінюються

в межах від —15" до -f-ІО". В другому ряді вони змінюють

ся повільніше — в межах від —6" до Отже, вже з цьо

го можна було зробити висновок, що другий ряд вимірів точ

ніший, ніж перший. Але цей факт змогла виявити лише се

редня квадратична помилка т.

В теорії імовірностей доводиться, що при нормальному

законі розподілу випадкових помилок вимірів між середньою

квадратичною помилкою і середнім з абсолютних значень

помилок існує така залежність:

0 = 0,7979 4/5 т, ? (16,9)

причому вона виявляється тим краще, чим більше число ви

мірів маємо в даному ряду. Якщо при достатньому числі ви

мірів рівінян.ня (16,9) не задовольняється, то можна вва

жати, що або даний ряд помилок підлягає якомусь іншому

закону розподілу, або результати втімірів містять невідомі

систематичні помилки. •

Таким чином, середня квадратична помилка є досить на

дійним і чутливим критерієм для оцінки точності, який ха

рактеризує умови вимірів. Певним умозам вимірів відповідає

своя середня квадратична помилка. Ця обставина має ве

лике практичне значення. Так, якщо ми з одного виміру,

проведеного при певних умовах, одержимо результат а, то,;

знаючи з попередніх досліджень середню квадратичну по

милку рг, яка відповідає цим умовам, ми можемо сказати,

що й .Даний результат одержано з тією самою середньою

квадратичною помилкою. Крім того, в теорії імовірностей

виявляється і теоретичне її значення, а саме: середня квад

ратична помилка є тим основним і єдиним параметром, який

при великому числі вимірів п визначає вид кривої нормаль

ного закону розподілу випадкових помилок за величиною і

знаком. Знаючи цей параметр, можна обчислити теоретичну

криву нормального розподілу помилок і порівняти її з кри

вою дійсного розподілу, що може виявити деякі особливості

даного ряду вимірів.

§ 17. ІМОВІРНА ПОМИЛКА

Імовірною помилкою називається таке

значення випадкової помилки щодо ї ї аб

солютної величини, по відношенню до яко

го при даних умовах р і в н о т о чни х вимірів

числа помилок більших і менших ВІД. неї'

є однаковим и.

Домовимось імовірну помилку позначати через р. Щоб;

знайти її, необхідно всі помилки результатів даного ряду

розташувати в ряд за зростанням їх абсолютних величин.

Тоді та помилка, яка стоїть посередині ряду при непарному

числі вимірів п, і буде імовірною. При п парному за імовір-,

ну помилку можна приймати середнє арифметичне з двох по

милок, що стоять посередині. Нехай маємо ряд помилок:

-0,1; 4-1,2; -0,9; -0,1; +5,6; -3,5; +0,6; -1,1; -0,5;

-2,0; -0,8; -> 0,9; -1,9; -1,8; +3,2; -0,5; +3,0; -4,4,

або, записавши їх в порядку зростання абсолютних ве

личин:

0,1; 0,1; 0,5; 0,5; 0,6; 0,8; 0,9; 0,9; 1,1;

1,2; 1,8; 1,9; 2,0; 3,0; 3,2; 3,5; 4,4; 5,6. (17,1)

Посередині цього ряду стоять дві помилки — 1,1 і 1,2,

Кожну з них можна прийняти за імовірну. Якби вони знач

но відрізнялися одна від одної, то за імовірну помилку мож

на було б взяти середнє арифметичне з них.

■ В теорії імовірностей доводиться, що між середньою

квадратичною та імовірною помилками при умові, що ломил-

ки підлягають нормальному закону розподілу, існує таке

співвідношення:

р = 0,6745 т ^ 2 /3 т, (17,2

причому воно тим точніше, ЧИМ (більше помилок буде/в ряду.

Основним недоліком імовірної помилки Р є те, що вона

зовсім не відображає характеру розсіювання помилок по їх

величині. Справді, уявимо собі, що в ряді помилок (17,1)

на останньому місці буде не 4,4 і 5,6, а 3,8 і 4,3. Очевидно, в

цьому випадку помилки: середня квадратична т і середня

з абсолютних значень 0 змінять свою величину, а імовірна

помилка залишиться тою самою. Через те в разі потреби

її краще обчисляти за формулою (17,2).

Для ілюстрації зв’язку між середньою, середньою квад

ратичною, граничною і імовірною помилками розглянемо та

кий приклад.

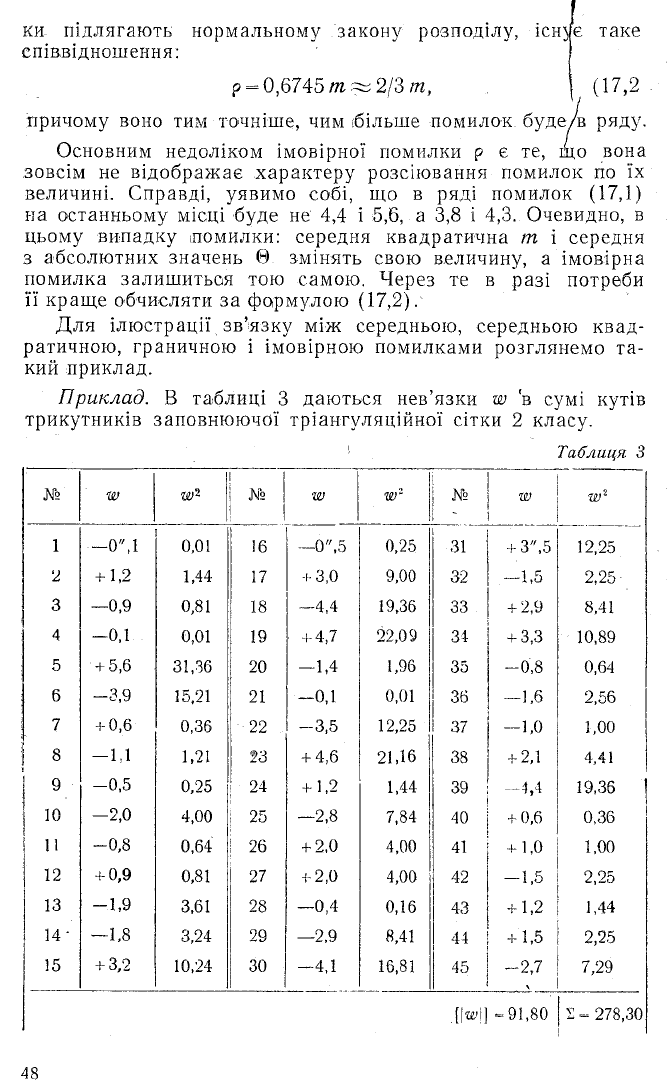
Приклад. В таблиці 3 даються нев’язки w 'в сумі кутів

трикутників заповнюючої тріангуляційної сітки 2 класу.

Таблиця З

№

W да2

№

w2 № W

чюг

1 —ОМ

0,01

—0",5

0,25

+ 3",5 12,25

2 + 1,2

1,44

+ 3,0 9,00

32 —1,5

2,25

—0,9

0,81 18

-4 ,4

19,36

+ 2,9

8,41

—0,1

0,01 19

+ 4,7 22,09 34

+ 3,3

10,89

+ 5,6

31,36

20 — 1,4

1,96

-0 ,8 0,64

-3 ,9

15,21 21 -0 ,1

0,01

36 —1,6

2,56

+ 0,6

0,36

-3 ,5 12,25

37 —1,0

1,00

— 1,1

1,21

23 + 4,6 21,16

+ 2,1

4,41

-0 ,5

0,25

+ 1,2 1,44

-4 ,4

19,36

—2,0

4,00 25

—2,8

7,84

40 + 0,6

0,36

-0,8

0,64 26

+ 2,0

4,00

41 + 1,0

1,00

+ 0,9

0,81 27 + 2,0

4,00 42

-1 ,5

2,25

13 -1 ,9

3,61 28

—0,4

0,16

+ 1,2

1,44

14-

—1,8

3,24 29 —2,9

8,41

+ 1,5

2,25

+ 3,2

10,24 ЗО —4,1 16,81

-2 ,7

7/29

,[І®[

- 91,80 £ = 278,30

Розг/ядаючи нев’язки трикутників як істинні помилки сум,

знайдемо:

1. Середню квадратичну помилку суми кутів одного три

кутника)

2. Середнє з абсолютних значень нев’язок:

3. Записуючи нев’язки в порядку зростання їх абсолютних

величин, посередині ряду (на 23 місці) знаходимо імовірну

помилку:

4. Знаходимо середнє з абсолютних значень помилок,

імовірну і граничну помилки за формулами зв’язку їх з се

редньою квадратичною помилкою:

Перевіримо, нарешті, даний ряд помилок на властивості

випадкових помилок.

1. Кількість помилок додатних — 19; сума їх дорівнює

+45",і. Кількість помилок від’ємних — 26; сума їх дорів

нює — 46",7.

2. Сума всіх помилок — Г',6, Середнє арифметичне з іс

тинних помилок:

є величина дуже мала.

3. Кількість помилок:

причому жодна з них не перевищує граничної, яка дорів-

ное +7",47. .

Таким чином, ми бачимо, що помилки даного ряду вимірів

підлягають нормальному закону розподілу помилок, або за

кону Гаусса.

р = 1 ",6 .

0 = %т =2',,49х4/5=Г,99)

р - 2/3 т = 2",49Х2/3 = 1",66,

ЛгРан= 3 т = 2",49хЗ = 7",47.

від 0 до ± 2",0 .„ 28,

„ ± 2", 1 „ ±4,0... 11,

„ ± 4", 1 „ ±6,0... 6,

§ 18. СЕРЕДНІ КВАДРАТИЧНІ ПОМИЛКИ ФУНКЦІЙ

НЕЗАЛЕЖНО ВИМІРЯНИХ ВЕЛИЧИН

Досі ми розглядали способи оцінки точності результатів

безпосередніх вимірів. Але часто трапляються випадки, коли

відшукувана величина не може бути виміряна безпс^середньо

і її доводиться визначати посередньо — шляхом обчнслеьь

як функцію безпосередньо і незалежно виміряних величин.

Коли б ці останні були виміряні абсолютно точно, то і знайде

на вартість функції була б точною. Але кожний вимір супро

водиться неминучими помилками. Отже, і значення функції

виміряних величин буде знайдено з деякою помилкою. В

зв’язку з цим виникає завдання — визначити середню квад

ратичну помилку функції виміряних аргументів.

Розв’яжемо цю задачу спочатку в загальному вигляді.

Нехай маємо істинне значення функції загального ви

гляду

F = F(X,Y), (18,1)

де X і Y — істинні значення аргументів.

Тут, для спрощення виводів, взято функцію лише двох

аргументів.

Функція (18,1) може бути складною, а тому перетворимо

її у більш простий лінійний вид. Для цього візьмемо досить

близькі до істинних наближені значення аргументів Х0 і К0,

причому

де (X) і (У) — істинні помилки величин Х0 і Y0.

Підставивши (18,2) в (18,1), одержимо:

Розкладемо (18,3) в ряд Тейлора, обмежуючись при роз

кладанні членами з малими величинами (А) і (Y) в перших

степенях:

наближеними значеннями аргументів А0 і Y0.

Нехай в результаті вимірів були одержані значення ар

гументів х і у, які зв’яжемо з їх наближеними значеннями

такими співвідношеннями:

F = F {Х0 — (Х), Y0-(Y)}.

(18,3)

F = F(X0, Г0) - О о(X ) - [% \(Y )t (18,4)

— часткові похідні функції, обчислені за

х = А0—(х),

У-Уо-(У)-

(18,5)