Бугай П.Т. Теорія помилок і спосіб найменших квадратів

Подождите немного. Документ загружается.

мірності, відомі під назвою властивостей випадкових поми

лок вимірів:

1) при да « и х умовах вимірів випадкові

помилки щодо своєї абсолютної величини

не можуть переходити певної границі;

2) малі щодо абсолютної величини по

милки зустрічаються частіше, ніж великі;

3) додатні помилки з’являються так са

мо часто, як і рівні їм щодо абсолютної

величини від’ємні помилки;

4) середнє арифметичне з випадкових

помилок результатів вимірів однієї і тієї

ж величини прямує до нуля при необме

женому зростанні числа вимірів;

5) у ряді випадкових помилок при пере

ході від одної помилки до сусідньої не по

винно бути помітно ніякої закономірно

сті в появі помилок щодо їх величини і

знака.

Всі ці властивості проявляються тим краще, чим більше

випадкових помилок будемо мати в даному ряду. Це є за

гальна особливість усіх статистичних закономірностей, яким

підлягають масові випадкові явища.

Перша властивість характеризує умови вимірів. Справді,

по величині граничної помилки ми можемо судити про

точність інструмента, майстерність і досвідченість спостері

гача, досконалість методів вимірів, наявність сприятливих

чи несприятливих зовнішніх умов. Ця властивість має прак

тичне значення ще й через те, що, знаючи з попереднього

досвіду граничну величину помилки, яку можна допустити

при даних умовах вимірів, ми можемо розрізняти грубі по

милки від великих, але ще допустимих випадкових помилок.

Друга властивість характеризує закономірність розподі

лу випадкових помилок за їх величиною.

Найбільше теоретичне і практичне значення для теорії

помилок мають третя і четверта властивості. Вони являють

собою прояв загального закону природознавства — закону

великих чисел, якому підлягають масові випадкові явища.

І Ц'й закон твердить, що сумісний вплив великої кількості

випадкових і незалежних між собою факторів на окремі ре

зультати вимірів будь-якої величини приводить до такого

остаточного її значення, яке майже не залежить від випад

ковості.

Четверту властивість випадкових помилок у математич

нім формі можна виразити так. Нехай маємо результати

ау, а2, а„ (12,1)

багатьох вимірів величини X. Різниці між результатами вимі

рів (12,1) і дійсним, або істинним значенням X відшукува

ної величини називаються істинними помилками. Домови

мось надалі позначати їх через

^1» ^2

■ • • > (12,2)

і обчисляти за правилом: «те, що є, мінус те, що повинно

бути», тобто

йі - Х = \і . (12,3)

Якщо число вимірів п буде досить велике, то на основі

третьої властивості випадкових помилок можна сподівати

ся, що в ряді помилок (12,2) кількість додатних і від’ємних

помилок буде приблизно однакова. Якщо ці помилки під

сумувати, то додатні з них компенсуватимуться від’ємними

і сума їх буде величиною конечною і притому малою. Поді

ливши її на досить велике число п, одержимо таке граничне

значення середньої помилки:

lim Аі + Д*+~ - +Ля = 0 . (12,4)

П-* ОО 11

Для позначення сум домовимося надалі вживати запро

понований Гауссом спеціальний значок [ ] :

Д,+Д2 + ... + Д„ = [А]. (12,5)

Тоді формулу (12,4) можна записати так:

lim ^ - = 0. (12,6)

Я- оо П

Однак необхідно зауважити, що при зростанні числа ви

мірів сума [Д] не прямуватиме до нуля. Во>на може то

збільшуватися, то зменшуватися і при цьому залишатиметь-

• • д [Д1

ся конечною і відносно малою величиною. Але вираз

завжди матиме тенденцію прямувати до нуля при необмеже

ному зростанні числа п.

Легко помітити, що четверта властивість випливає з тре

тьої. Вона виражає закономірність компенсації випадкових

помилок в середньому з результатів багатьох вимірів.

П’ята властивість випливає з тих характерних особливо

стей випадкових факторів, які обумовлюють появу в резуль

татах вимірів випадкових помилок, про що ми докладно го

ворили в § 11.

§ 13. МЕТОД ВИЯВЛЕННЯ ВЛАСТИВОСТЕЙ

ВИПАДКОВИХ ПОМИЛОК ЕКСПЕРИМЕНТАЛЬНИМ ШЛЯХОМ

Найпростіший спосіб експериментального дослідження

властивостей випадкових помилок полягає ось в чому.

Вимірюємо-з однаковою точністю і багато разів одну і

ту ж величину, намагаючись організувати виміри так, щоб в

них були відсутні грубі та систематичні помилки. Позначи

мо результати вимірів через

> ^'3 ї • • • > aN.

Припустимо тепер, що нам відоме істинне значення X ви

мірюваної величини з яких-небудь теоретичних міркувань.

Знаходимо істинні помилки:

о ,- =

X — А2, (13,1)

о д- —X == Дд' -

В тому випадку, коли істинне значення X вимірюваної ве

личини нам невідоме, для дослідження помилок замість ньо

го можна взяти середнє арифметичне

*0 = -&] (13,2)

або значення, знайдене з попередніх більш точних вимірів.

Далі розподіляємо окремі помилки щодо їх величини і

знака на окремі групи з певним інтервалом між ними і під

раховуємо кількість помилок:

ти т2, тг, ,

Я], Ті‘2і па, ... ,

що входять в групи.

Ці помилки знаходяться в границях відповідно

від 0 до +*!, від 0 до —хи

п "І" -^1 п "Ь Х2, П X] „ Х2,

„ |- Хо „ + Xg, „ Х г „ Л"5,’

де величина хі+і—хі =о^ = const.

За цими даними будуємо на графіку послідовно прямокут

ники з основами ± (хі+і — Хі ) = ох, які відкладаємо по осі

х, і відповідними їх висотами mь т 2, . . . , пи п2, . . . , рівними

кількості помилок® інтервалах, які відкладаємо по осі у. Та

ким чином одержуємо графічне зображення закону розподілу

Й II. Т. Нуглії

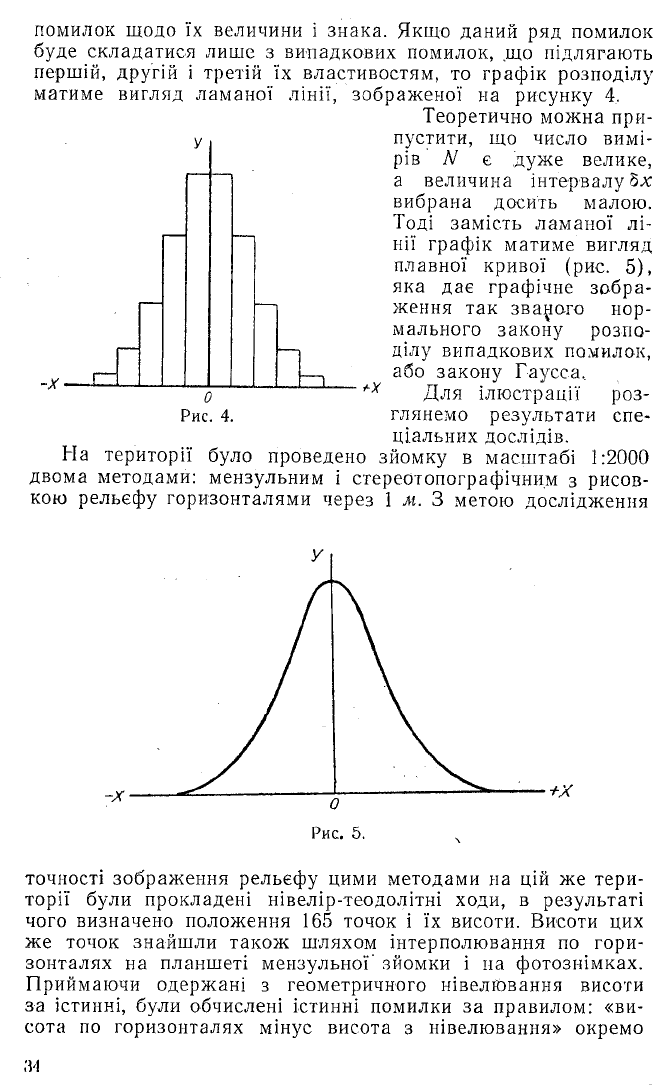
помилок щодо їх величини і знака. Якщо даний ряд помилок

буде складатися лише з випадкових помилок, що підлягають

першій, другій і третій їх властивостям, то графік розподілу

матиме вигляд ламаної лінії, зображеної на рисунку 4.

Теоретично можна при

пустити, що число вимі

рів N є дуже велике,

а величина інтервалу5х

вибрана досить малою.

Тоді замість ламаної лі

нії графік матиме вигляд

плавної кривої (рис. 5),

яка дає графічне зобра

ження так званого нор

мального закону розпо

ділу випадкових помилок,

або закону Гаусса..

Для ілюстрації роз

глянемо результати спе

ціальних дослідів.

На території було проведено зйомку в масштабі 1:2000

двома методами: мензульним і стереотопографічним з рисов

кою рельєфу горизонталями через 1 м. З метою дослідження

-х-

Рис. 4.

точності зображення рельєфу цими методами на цій же тери

торії були прокладені нівелір-теодолітні ходи, в результаті

чого визначено положення 165 точок і їх висоти. Висоти цих

же точок знайшли також шляхом інтерполювання по гори

зонталях на планшеті мензульної" зйомки і на фотознімках.

Приймаючи одержані з геометричного нівелйвання висоти

за істинні, були обчислені істинні помилки за правилом: «ви

сота по горизонталях мінус висота з нівелювання» окремо

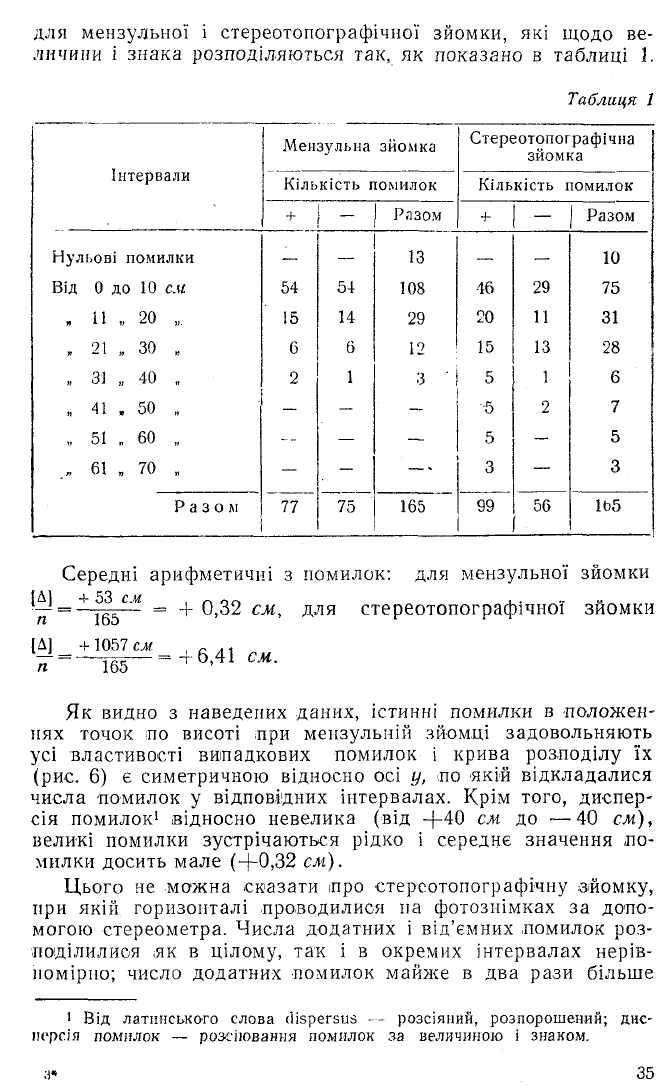
для мензульної і стереотопографічної зйомки, які щодо ве

личини і знака розподіляються так, як показано в таблиці 3.

Таблиця І

Інтервали

Мензульна зйомка

Стереотопографічна

зйомка

Кількість помилок

Разом

Нульові помилки

— —

Від 0 до 10 см 54

108

. 11 „ 20 „

20 11

, 21 „ ЗО „

„ 31 „ 40 , 2

3 '

„ 41 . 50 „

—

,, 51 „ 60 „

— —

61 , 70 „

—

— -

—

Р а з о м

75 165

99 56

ІЬ5

Середні арифметичні з помилок: для мензульної зйомки

= = ^ см' для стеРеотопогРаФічної зйомки

[Д] +1057 см

п ~ 165

= -І 6,41 см.

Як видно з наведених даних, істинні помилки в положен

нях точок по висоті при мензульній зйомці задовольняють

усі властивості випадкових помилок і крива розподілу їх

(рис. 6) є симетричною відносно осі у, по якій відкладалися

числа помилок у відповідних інтервалах. Крім того, диспер

сія помилок1 відносно невелика (від +40 см до — 40 см),

великі помилки зустрічаються рідко і середнє значення по

милки досить мале (+0,32 см).

Цього не можна сказати про стереотопографічну зйомку,

при якій горизонталі проводилися на фотознімках за допо

могою стереометра. Числа додатних і від’ємних помилок роз

поділилися як в цілому, так і в окремих інтервалах нерів

номірно; число додатних помилок майже в два рази більше

і Від латинського слова dispersus — розсіяний, розпорошений; дие

т'рсія помилок — розсіювання помилок за величиною і знакоіи.

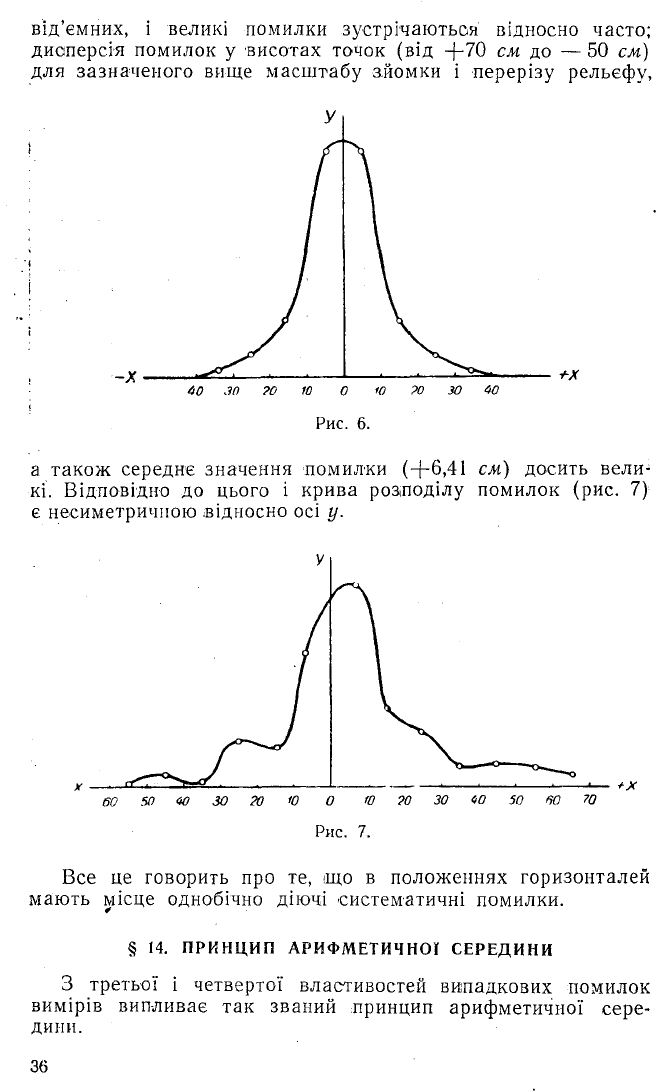
від’ємних, і великі помилки зустрічаються відносно часто;

дисперсія помилок у висотах точок (від +70 см до — 50 см)

для зазначеного вище масштабу зйомки і перерізу рельєфу,

Рис. 6.

а також середнє значення помилки (+6,41 см) досить вели

кі. Відповідно до цього і крива розподілу помилок (рис. 7)

є несиметричною відносно осі у.

Рис. 7.

Все це говорить про те, що в положеннях горизонталей

мають місце однобічно діючі систематичні помилки.

§ 14. ПРИНЦИП АРИФМЕТИЧНОЇ СЕРЕДИНИ

З третьої і четвертої властивостей випадкових помилок

вимірів випливає так званий принцип арифметичної сере

дини.

Нехай маємо результати

аи а2, ... , ап (14,1)

багатьох безпосередніх і р-івноточних вимірів однієї величи

ни, істинне значення якої нехай ібуде X. Позначаючи через

Aj, Д2, .. . , Ап

істинні помилки результатів вимірів (14,1), можемо 'напи

сати ряд таких рівностей:

а1—Х = А1,

0-2 X — Д2, (14,2)

&п X — Ад.

Підсумувавши ці рівності, після ділення на число ви

мірів п одержимо:

[а]-пХ-Щ ,

И _ х = ^-] О 4’3)

п п

Величина ^ є середнє арифметичне з результатів вимі

рів, а величина ~ — середнє арифметичне з істинних поми

лок вимірів. Позначимо їх відповідно через Х0 1 Д„ . Тоді

рівність (14,3) можна записати так:

* -= * 0-Д 0. (14,4)

Очевидно, що величина Д0 є не що інше, як істинна ви

падкова помилка середнього арифметичного Хо-

Припустимо тепер, що число вимірів п необмежено зро

стає. Тоді на основі четвертої властивості випадкових поми

лок граничне значення помилки Д0 середнього арифметично

го буде дорівнювати:

lim — =1ітД0 =О. (14,5)

П-ю° П П-*°°

Звідси, зважаючи на (14,4),

[n Z Xo = X ’ П4-6)

тобто середнє арифметичне з результатів

рівноточних вимірів однієї і тієї ж в е л и -

чини прямує до істинного значення цієї

величини при необмеженому зростанні

числа вимірів. Це положення і виражає принцип

арифметичної середини.

З попереднього викладу .видно, що вивід формули (14,6)

базується на двох припущеннях.

По-перше, помилки вимірів (14,2) повинні бути лише

випадковими і підлягати третій їх властивості. Формула не

буде вірною, якщо виміри будуть обтяжені, крім випадко

вих, ще й систематичними .помилками. Справді, припусти

мо, що

— -^Ч-Д^ + 0j,

а2 =Л'+Д2' + о2, (14,7)

dn = X + Д Л , + вп ,

де А/, А/,.. ., А„' — випадкові, а о1( з2,.. ., ап — систематичні

частини загальної величини Апомилок вимірів. Знайдемо

суму рівностей (14,7). Після ділення її на число вимірів п

будемо мати:

* 0 = * + ^ ! + Ы (14,8)

При необмеженому збільшенні числа вимірів п середнє

арифметичне з випадкових частин помилок прямуватиме до

нуля. Величина ж ~ завжди залишатиметься конечною.

Отже, середнє арифметичне Х0 буде відрізнятися ‘від істин

ного значення X на якесь середнє значення систематичної по

милки о0. Цю обставину завжди треба мати на увазі при

застосуванні принципу арифметичної середини для обробки

результатів вимірів.

По-друге, число вимірів повинно бути дуже великим. Але

в дійсності для практичних потреб їх роблять до 20—ЗО і ли

ше в деяких випадках більше.

Однак і при конечному числі вимірів за найбільш надій

не значення вимірюваної величини приймають середнє ариф

метичне, тому що, беручи до уваги третю властивість випад

кових помилок, яка виражає закон компенсації в середньо

му з випадкових помилок, дріб~ = А0 буде величиною від

носно малою і притому тим меншою, чим точніше проводи

тимуться виміри і чим більше їх буде.

Таким чином, при обробці ■•результатів конечного числа

рівноточних вимірів однієї величини користуються таким

важливим і основним положенням теорії помилок: серед

нє арифметичне є найбільш надійним, або

найімовірнішим значенням вимірюваної

величини, яке можна одержати з результа

тів конечного числа рівноточних вимірів

цієї величини.

§ 15. МАТЕМАТИЧНІ ВЛАСТИВОСТІ СЕРЕДНЬОГО

АРИФМЕТИЧНОГО

В попередньому параграфі ми в1вели дуже важливе для

теорії помилок поняття середнього арифметичного. Згідно з

визначенням, середнє арифметичне дорівнює сумі даних ве

личин, поділеній на їх число. Позначаючи через її, U, . . ., U

дані величини, а через L0 -— середнє арифметичне з них, ма

тимемо:

г /і + /2+. ..+//<

. 0 п '•

або

A0- [f ' (15,1)

звідки

/*/.„-[/] =0. (15,2)

Доведемо дві важливі властивості середнього арифметич

ного, не залежні від фізичного значення тих величин; з яких

воно виводиться.

1) Знайдемо різниці між середнім арифметичним L0 і да

ними величинами Л, /г, . . ■ , In'.

Lq — 1j = v!,

Lo—h =v2, (15,3)

L0 In — ‘Vn -

Різниці vu v2, . . . , vn називаються відхиленнями даних

величин від їх середнього арифметичного. Підсумуємо тепер

рівності (15,3):

nL0-[l]-[v]. (15,4)

Але, згідно з формулою (15,2), ліва частина цієї рівності

дорівнює нулю, а тому

М =0, (15,5)

тобто алгебраїчна сума відхилень даних ве

личин від їх середнього арифметичного до

рівнює кулю.

Формула (15,5) буде справедливою в тих окремих ви

падках, коли в межах потрібної точності обчислень середньо

го арифметичного сума [/] точно ділитиметься на число ви

мірів п. Але часто бувають .випадки, коли ця умова не задо

вольняється. Тоді, обчислюючи середнє арифметичне до пев

ного десяткового знака, ми одержимо не точне його значен

ня Lo, а лише наближене L 0', яке відрізнятиметься від точ

ного на величину , де а — остача від ділення, тобто

Lo = W + i - (15,6)

Знайдемо тепер, чому в цьому випадку буде дорівнюва

ти сума відхилень Vi ' даних величин від неточного значення

L'о середнього арифметичного.

Запишемо ряд рівностей:

L0'- l x = vx',

Z.Q ^2 = >

L0 In — “Vп •

Сума їх дорівнюватиме:

nL0'-[l]=[v']. (15,7)

Беручи до уваги (15,5) і (15,6), знайдемо різницю рівно

стей (15,4) і (15,7):

п (z-o' + ^ ) — М =°.

nw - [/] = [V'], (15,8)

а - - [ « '].

Отже, сума [v'] відхилень, взята з оберненим знаком,

дорівнює остачі я від ділення [/] на число вимірів п.

Формули (15,5) і (15,8) будуть контрольними при об

численні середнього арифметичного.

2) Для доведення другої властивості візьмемо замість

середнього арифметичного якесь інше довільне число L' і

знайдемо «ові відхилення Ьі даних величин від нього:

Z. /і = Oj,

£ '-/а = 82. (15,9)

L' — ln = 3„ .

Порівняємо тепер відхилення v1,v2,...,vni 8j,S2,...,§„. Для

цього знайдемо різниці між відповідними рівностями (15,3) і

(15, 9). Одержимо:

L L0 = ol- і>і,

Z/-Z.0 = 8a-® 2, (15,10)

L Lq — Vn •