Брунауер С. Адсорбция газов и паров

Подождите немного. Документ загружается.

ТЕПЛОТА АДСОРБЦИИ I

г:.-,

чается суммированием ориентационного, индукцион-

ного и дисперсионного потенциалов 11^, и II соот-

ветственно даваемых уравнениями (4), (8) и (14):

(18)

Поучительно сравнить относительн^гю величину

этих трех эффектов для некоторых простых диполь-

ных молекул. В табл. 19, взятой у Лондона, ука-

заны величины энергш! для шести молекул. Во вто-

Таблица 19

Ориентацнонные, индукционные и днспсрснонные энергии

Газ 10"»

а. 10^'

Н:„

еУ

Уо

ярг

см"

эрг

см^

эрг

см^

СО

0,12 1,99 14,3

0,0034

0,057

67,5

111

0,:-8

5,4 12 0,35

1,68

382

НВР

0,78 3,58 13,3 6,2 4,05

176

ПС1

1,03

2,63

13,7

18,6 5,4

105

N1-13

1,5 2,21

16 84 10

Н2О

1,84

1,48

18 190

10 47

ром, третьем и четвертом столбцах содержатся ди-

польные моменты, поляризуемости и характеристи-

ческие энергии для шести газов. В пятом, шестом и

седьмом столбцах даны ориентационные, индукцион-

ные и дисперсионные энергии, вычисленные с помош,ью

уравнения (18). Индукционный эффект всегда мал, его

величина составляет, самое большее, 5% от обш;его

ван-дер~ваальсова притяжения. Ориентационный эф-

фект исчезаюш,е мал для молекул, имеюш,их малые

дипольные моменты, как СО и Н1, и он много меньше,

чем дисперсионный эффект да;ке для молекул, имею-

щих столь большой дипольный момент, как НС1.

Только До^я молекул, обладающих очень большими

дипольными моментами, как ННз и Н2О, ориентацион-

ны1"1 эффект становится равным илп большим, чем

дисперсионный эффект, и последний никогда не ста-

новится исчезающе хмалым.

262 ГЛАВА VI >

Согласно уравнению (18) для молекул, не имеющих

постоянных диполей, ван-дер-ваальсов потенциал обу-

словливается исключительно дисперсионным эффек-

том, так как [л=0. Однако ото не вполне справедливо;

уравнение (14) пе представляет полностью ван-дер-

ваальсов потенциал для всех расстояний даже и для

атомов благородных газов. При малых значениях г

долишы учитываться два других эффекта: дополни-

тельный притягательный член и энергия отталкивания.

Как мы видели, член энергии притяжения, выра-

укенный уравнением (16), возник из рассмотрения

флюктуирующих диполей, которыми обладают даже

неполярные молекулы. Однако, кроме этих флюктуи-

рующих диполей, молекула обладает также флюктуи-

рующими квадруполями. Они индуцируют диполи в

соседних молекулах, и энергия взаимодействия между

флюктуирующим квадруполем и индуцированным ди-

полем дается выражением

(19)

где В — константа. Уравнение (19) аналогично урав-

нению (12), которое представляет потенциал взаимо-

действия ме?кду постоянным квадруполем и индуциро-

ванным дипольным моментом. Маргенау вычислил

взаимодействие флюктуирующий квадруполь— индуци-

рованньп! диполь для атомов водорода и гелия и на-

шел, что для малых расстояний им нельзя пренебречь

по (^равнению с взаимодействием флюктуирующий ди-

поль — индуцированный диполь. Для двух атомов

1^елия при равновесном расстоянии в 2,9 А взаимодей-

ствие квадруполь — диполь составляет до 26% взаи-

модействия диполь — диполь.

В полном выражении потенциала ван-дер-ваальсо-

вого притяжения неполярпых молекул имеются также

высшие члены взаимодействия по сравнению с приве-

денными в уравнении (19). Ближайший высший член

представляет взаимодехгствие флюктуирующий квад-

руполь — индуцированный квадруполь, которое изме-

няется обратно пропорционально Этим членом,

ТЕПЛОТА АДСОРБЦИИ I г:.-,

однако, всегда можно пренебречь. Маргенау вычислил,

что для двух атомов гелия при равновесном расстоя-

нии член квадруполь — квадруполь составляет толь-

ко 3% от члена диполь — диполь.

Вторым энергетическим членом, весьма ва/кным

для малых расстояний, является энергия ван-дер-

ваальсового отталкивания. В начале этого раздела

было отмечено, что если две молекулы подходят до-

статочно близко друг к другу, то они друг друга от-

талкивают.

Первоначально потенциал отталкивания был вы-

ражен в форме обратно!! степенной функции, вполне

подобной членам притяжения;

(20)

где В' и п — константы. Леннард-Джонс опреде-

лил величину п из вириальных коэффициентов газов

и нашел, что 71=12 дает наилучшие результаты, хотя

даже столь низкие величины п, как 9 и 10, могли бы

подойти к экспериментальным данным при соответ-

ствующем подборе константы В'. Квантовая механика,

однако, показала, что отталкивательный потенциал

более правильно выражается экспоненциальным за-

коном

(21)

где и ро — константы, которые могут быть вычислены

из опытных данных.

Энергия ван-дер-ваальсового взаимодействия между

двумя неполярными молекулами выражается суммой

IIг, ии На основании уравнений (21), (16) и (19)

она может быть записана в форме

и = (22)

Первый и третий члены в правой части уменьшаются

много быстрее с ростом г, чем второй член; они важны

поэтому только для малых расстояний. Кроме того,

энергия оттаV^киваиия по лежите льна, а квадруполь-

264 ГЛАВА VI >

дипо,1Ьный член отрицателен, и таким образом оба

члена частично друг друга компенсируют. Поэтому,

пренебрегая ими в некоторых расчетах по сравнению

со вторым членом, не совершают серьезной ошибки.

Мы обсудим теперь две проверки теории Лондона,

в которой допускается, что первый и третий члены

уравнения (22) столь малы, что ими можно пренебречь,

и ван-дер-ваальоово взаимодействие приписывается ис-

ключительно диполь-дипольному члену.

Первой из этих проверок является вычисление кон-

станты Ван-дер-Ваальса а из дисперсионного эффекта.

Ван-дер-ваальсовы константы а п Ь связаны с констан-

той дисперсионной энергии С уравнением

(23)

где Л'^ — число Авогадро. Лондон [Ю] вычислил С с

помощью уравнения (17), а затем, пользуясь опытным

значением 6, вычислил а по уравнению (23). Резуль-

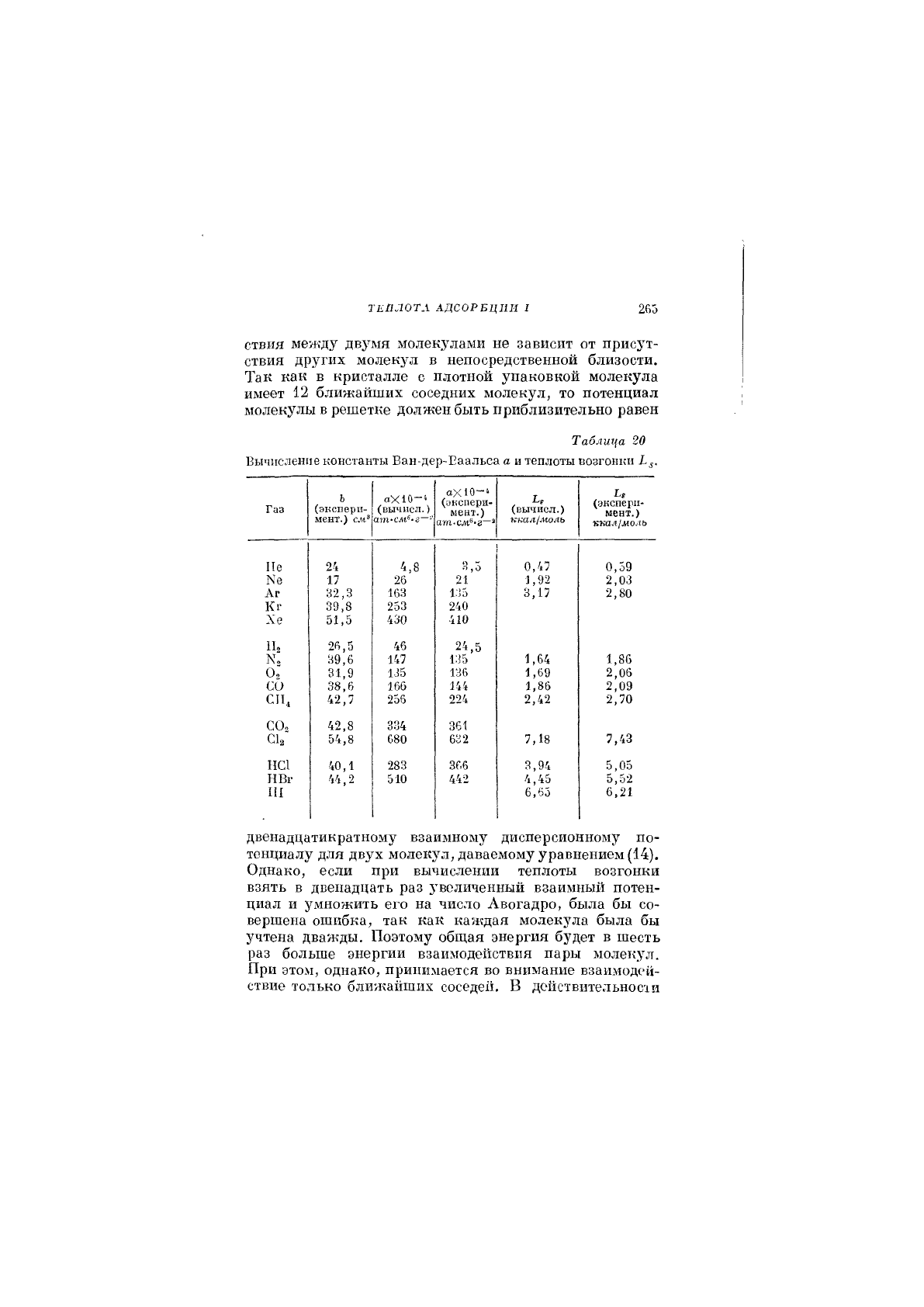
таты приведены в табл. 20. Сравнение третьего и чет-

вертого столбцов показывает очень хорошее согласие

между теоретическими и экспериментальными значе-

ниями а. Так как экспериментальные значения а мо-

гут содержать ошибку, достигающую 30%, и так как

пренебрежение двумя членами в уравнении (22) может

внести ошибку приблизительно такого же порядка в

вычисление а, то согласие между абсолютными вели-

чинами должно рассматриваться как случайное.

С другой стороны, согласие между относительными ве-

личинами при изменении а в 150 раз не может быть

приписано случайности; следовательно, надо сделать

заключение, что эти вычисления подтверждают тео-

рию Лондона.

Второй проверкой теории Лондона является вы-

числение из дисперсионного эффекта теплот возгонки

кристаллических веществ с молекулярными решетками.

В этом вычислении надо принимать во внимание силы

взаимодействия данной молекулы со всеми ее сосе-

дями. Лондон[®] доказал, что дисперсионные силы

аддитивны, т.е.; что сипа (или потенциал) взаимодей-

ТЕПЛОТА АДСОРБЦИИ I

г:.-,

ствия между дв}шя молекз^лами не зависит от присут-

ствия других молекул в непосредственной близости.

Так как в кристалле с плотной упаковкой молекула

имеет 12 ближайших соседних молекул, то потенциал

молекулы в решетке должен быть приблизительно равен

Таблица 20

Вычисление константы Ван-дер-Еаальса

и теплоты возгонки

Газ

(экспери-

мент.) см'

оХ10-«

(вычисл.)

ат-см"-г—-

аХЮ-'

(экспери-

мент.)

Ьр

(вычисл.)

пкал/моль

(экоперп-

мент.)

ккал1моль

Не

4,8

3,5

0,47

0,59

Ке 17 26

1,92

2,03

АР 32,3

163 135

3,17

2,80

Кг

39,8

253 240

Хе 51,5 430

410

112

2(^,5

24,5

К, 39,6

147 135

1,64

1,86

о1

31,9

135

136

1,69

2,06

со

38,6 166 144 1,86 2,09

СП,

42,7

256

224

2,42 2,70

СОг

42,8 334 361

СИ

54,8 680 632 7,18

7,43

НС1 40,1

283 366

3,94

5,05

НВГ 44,2 510 442 4,45

5,52

П1

44,2

6,65 6,21

двенадцатикратному взаимному дисперсионному по-

тенциалу для двух молекул, даваемому уравнением (14),

Однако, если при вычислении теплоты возгонки

взять в двенадцать раз ^Увеличенный взаимный потен-

циал и умножить его на число Авогадро, была бы со-

вершена ошибка, так как каждая молекз'ла была бы

учтена дважды. Поэтому обш,ая энергия будет в шесть

раз больше энергии взаимодействия пары молекул.

При этом, однако, принимается во внимание взаимодей-

ствие только ближайших соседей. В действительное!и

266 ГЛАВА VI >

более удаленные молекулы также делают некоторый

вклад в энергию притяжения, так что общая энергия

в 7,38 раза больше энергии взаимодействия пары мо-

лекул. Расстояние, па которое сближены молекулы в

решетке, получается из плотности кристалла.

Для скрытой теплоты возгонки Лондон дает

форм}'лу

I = 3,04

• 10-52

^ кал]моль, (24)

где

— плотность, М — молекулярный вес ш С —

константа дисперсионной энергии, вычисленная по

уравнению (17). Чтобы избежать усложнений, вызван-

ных термическим движением, Лондон привел опытные

значения ^ и § к 0°К. Результаты показаны в двух

последних столбцах табл. 20. Согласие между теорией

и опытом снова вполне удовлетворительное. Спе-

циальный интерес представляет ряд галоидоводоро-

дов. Несмотря па то, что дипольный момент сильно

уменьшается от хлористого водорода к иодистому во-

дороду (табл. 19, второй столбец), теплота возгон-

ки возрастает, указывая на то, что большая часть

ван-дер-ваальсовой энергии не может быть обязана

постоянным диполям, которыми эти молекулы обла-

дают.

Вскоре после появления труда Лондона проблема

лголекулярных сил между неполярными молекулами

была рассмотрена Слэтером и Кирквудом[1з] на ос-

нове совершенно другого квантово-механического под-

хода. Применяя вариационный метод для определения

энергии возмущения, они получили для взаимного

потенциала двух подобных молекул выражение

где е п т — заряд и масса электрона, а — поляризуе-

мость и — число электронов в наружной оболочке.

Соотношение между уравнением (25) и уравнением

Лондона (14) может быть рассмотрено лучше, если

ТЕПЛОТА АДСОРБЦИИ I г:.-,

представить последнее в форме

РО)

где / дается выражением

1 = . (27)

Член / дает эффективное число электронов, вызываю-

щих дисперсию. Обычно его обозначают как «вели-

чину /» дисперсионной кривой. Сравнение уравнений

(25) и (26) показывает, что / в уравнении Лондона за-

меняется на в уравнении Слэтера и Кирквуда. Так

как обычно больше, чем то дисперсионная энер-

гия обычно больше, чем ^/д.

Хотя трактовка Лондона имеет большую общность,

Слэтер и Кирквуд достигли поразительного успеха в

своих вычислениях молекулярных сил между атомами

гелия. Их метод хорошо примешьм также для основ-

ного вычисления поляризуемостеп. Для поляризуе-

мости гелия опп получили величину в 0,210-сл®,

которая очень хорошо согласуется с эксперименталь-

ной величиной в 0,205-10"-^ см". Для потенциала

взаимодействия двух атомов гелия авторы вывели урав-

нение

орг, (28)

где Яд— радиус боровскоп орбиты водорода.

Применяя это выражение для междумолекз^дяр-

ного потенциала, Кирквуд и Кейс[1''] вычислили вто-

рой вириальный коэффициент гелия при разных тем-

пературах и получили превосходное согласие с опы-

том. С помощью теоретического значения второго

вириального коэффициента они вычислили также дру-

гие величины, характеризз^ющие физические свойства

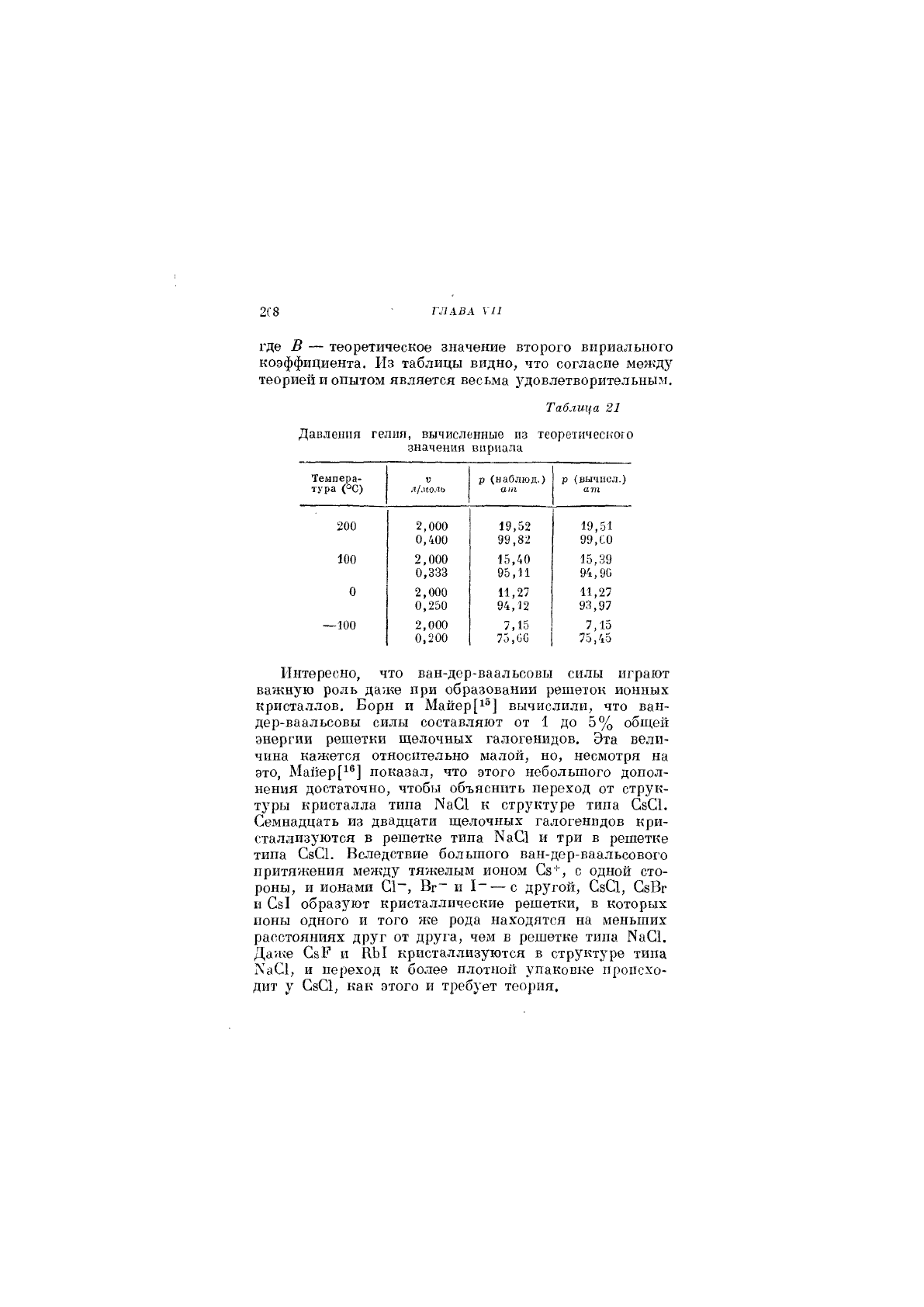
гелия. Пример этих расчетов показан в табл. 21.

Давление гелия было вычислено при нескольких тем-

пературах и объемах с помощью уравнения

Р = (ЙГ/г) (1 -Ь (29)

27'(

ГЛАВА VII

где В — теоретическое значение второго вириалыюго

коэффициента. Из таблицы видно, что согласие между

теорией и опытом является весьма удовлетворительным.

Таблица 21

Давления гелия, вычисленные из теоретического

значения вприала

Темпера- гз

р (ыаОлюд.)

р (ЕЫЧНСЛ.)

тура (ОС)

л/моль

ат

200 2,000

19,52 19,51

0,400

99,82

99, СО

100 2,000 15,40

15,39

0,333

95,11 94,9С

2,000

11,27 11,27

0,250

94,12

93,97

—100

2,000

7,15

0,200 75,00

75,45

Интересно, что ван-дер-ваальсовы силы играют

важную роль даяад при образовании решеток ионных

кристаллов. Борн и Майер[1®] вычислили, что ван-

дер-ваальсовы силы составляют от 1 до 5% общей

энергии решетки щелочных галогенидов. Эта вели-

чина кажется относительно малой, но, несмотря на

это, Майер[1®] показал, что этого небольшого допол-

нения достаточно, чтобы объяснить переход от струк-

туры кристалла типа к структуре типа СбС!.

Свхмнадцать из двадцати щелочных галогенпдов кри-

сталлизуются в решетке типа КаС1 и три в решетке

типа СзС!. Вследствие большого ван-дер-ваальсового

притяжения между тяжелым ионом

С8 + ,

с одной сто-

роны, и ионами С1~, Вг~ и 1" — с другой, СзС!, СзВг

и Сз! образуют кристаллические решетки, в которых

ионы одного и того же рода находятся на меньших

расстояниях друг от друга, чем в решетке типа КаС1.

Да;ке СзР и КЫ кристаллизуются в структуре типа

КаС1, и переход к более плотной упаковке происхо-

дит у СзС!, как этого и требует теория.

'ГКПЛчТА АДСОРВЦПП I 709

Общая теория теплоты адсорбции

Развитие теории теплоты ван-дер-ваальсовой ад-

сорбции близко следовало за развитием теории ван-

дер-ваальсовых сил. Хотя Сосюр ["] уже в 1814 г.

показал, что большая часть легко конденсирующихся

газов адсорбируется в больших количествах множе-

ством адсорбентов, прошло еще столетие, прежде чем

Эйкен[^®] впервые попытался количественно доказать,

что «адсорбционные силы, по крайней мере в случае

так называемой физической адсорбции, являются в ос-

новном теми ?ке, что и при обычном молекулярном при-

тяженип>.

Эйкен допустил, что потенциал притяжения между

поверхностью и молекулой газа может быть выражен

обратным степенным законом

? = (30)

где г — расстояние между поверхностью и молекулой

газа, а а-^ ш т — константы*. Концентрации адсорби-

руемого вещества на расстоянии г от поверхности и

в газовой фазе могут быть получены из закона рас-

пределения Максвелла — Больцмана

(31)

где с^ и с^ — соответственно концентрации газа на

расстоянии г от поверхности и в газовой фазе. Адсор-

* Соотношение между адсорбционным потенциалом (р и

потенциалом Поляии е дается вырашением

где Е^ — теплота конденсации газа. Адсорбционный потен-

циал отличается от теплоты адсорбции теплотой сжатия, ко-

торой часто можно пренебречь. В этой главе термины а д с о р б-

ционный потенциал и теплота адсорб-

ц и и применяются равнозначно. Соотношение между этими

и другими энергетическими терминами детально обсуждается

в гл. VIII.

270 ГЛЛПЛ VII

бированпое количество выражается через

« = л 5 (с, — с^) ^г = Ас^ -1)<1г, (32)

ГЦ Г„

где V — число молей адсорбированного газа, А —

величина поверхности адсорбента и г^ — ближайшее

расстояние, на которое молекула газа может прибли-

зиться к поверхности. Эйкен допустил, что г^ равно

радиусу адсорбированной молекулы. Для и^АТ в

резЛ'Льтате интегрирования получаем;

1- — Агие^-''"^ (33)

причем

ш)

= (34)

Так как имеет размерность энергии, а к — кон-

станта Больцмана с размерностью энергии, деленной

на градус, то С^ имеет размерность температуры.

представляет величину работы, необходимо!! для

того, чтобы перенести один моль адсорбированного

газа на бесконечное расстояние от поверхности. Член

6 (те) в уравнении (33) является функцией от т, ко-

торым обычно можно пренебречь по сравнению с

тС^Т. Пренебрегая этим членом и вводя давление

газа вместо концентрации, т. е. р=с^ЯТ, мы получаем:

(35)

р ВС^т

При постоянной температуре все величины в пра-

во!! части уравнения (35) постоянны. Поэтому урав-

нение Эйкена приложимо только к линехшой началь-

Н011 части изотермы адсорбции. Эйкен не сделал

попытки вывести закон для силы притяжения из основ-

ных физических соображений и просто оценил т —

пе-казатель степени г в уравнении (30) — из самой изо-

термы адсорбции. Он достиг успеха в применении

уравнения для адсорбционных данных Гомфрей[1®]