Беляев Е.Ф., Шулаков Н.В., Дискретно-полевые модели электрических машин, учебное пособие

Подождите немного. Документ загружается.

семейство разностных задач, которое называется разностной схемой

[24].

При решении краевых задач возможны два варианта аппрокси-

мации:

Явная схема:

иг-и\

At h

= -

(и'

-2и1+ии) + /'

(3.69)

Такая схема называется явной, потому что позволяет определить

значение функции в каждой точке исследуемой области Е/"

, выра-

жая его через известные её значения на предыдущем временном ин-

тервале Ui:

= и\ + - 2 и; +£/•_[) + /) At. (3.70)

Таким образом, зная начальные значения функции во всей ис-

следуемой области, можно рассчитать её значения на последующих

временных интервалах.

2. Неявная схема:

=4(К\ - ж?

+и)+/;. (з.?1)

At h

Преобразуем это уравнение и запишем его в виде

Щ-и?! -fl+2^Vr

+—-£/!;!

-V! +

T')

V (3.72)

hx \ hi J hx

В этом уравнении известна правая часть, однако неизвестны зна-

чения искомой функции на новом временном слое [/$, U'*\ и]1\.

Для нахождения этих значений необходимо решить систему трёх-

членных алгебраических уравнений, что значительно сложнее, чем

нахождение этих величин в явной схеме.

Казалось бы, что использование явных схем предпочтительнее,

так как они позволяют получать решение краевой задачи за более

короткое время. Однако в настоящее время эти схемы применяются

относительно редко, поскольку они являются условно устойчивы-

ми. Явные схемы могут использоваться лишь при определённом

соотношении между временными и пространственными интервала-

ми At и h

Поясним условия устойчивости явной схемы, для чего запишем

её в следующем виде:

1-2

kjht

hi j

U'i + Fih,-

(3.73)

В силу линейности решаемой задачи аналогичное уравнение оказы-

вается справедливым и для погрешности

kih,

е.

(3.74)

гх

где погрешность е; представляет собой разницу между точным ре-

шением дифференциального уравнения задачи U\ и точным решени-

ем разностного уравнения U\:

(3.75)

Положим, что в исследуемой области максимальное значение

погрешности достигается в точке

М:

тах|е,| =

е'

Тогда заведомо справедливо соотношение

kJ + N-.N

KI (3.76)

и для максимума погрешности уравнение (3.74) записывается в виде

»4<*'

' 2lr'

M - ,

1-2

kiht

-MI

(3.77)

Если 1-2^~>0 или то |е'

| <|е'| , и каждое после-

hl ki

1 ]м 1 1м

дующее значение погрешности оказывается меньше предыдущего,

т.е. нарастания погрешности не происходит. Таким образом, для ус-

тойчивости счёта необходимо, чтобы интервалы разбиения про-

странственной и временной координат были связаны соотношением

(3.78)

2 К

Отсюда следует, что при больших значениях коэффициента

уравнения К(х, t) приходится выбирать временной интервал

А?

очень

малым, и решение дифференциального уравнения требует больших

затрат времени.

Неявная схема (3.71) является безусловно устойчивой: по-

грешности расчёта, возникающие в процессе решения системы ал-

гебраических уравнений, затухают при любом соотношении между

временным и пространственным интервалами. Выбирая временной

интервал достаточно большим (исходя из величины допустимой

погрешности), можно значительно сократить время решения диф-

ференциального уравнения независимо от значений его коэффици-

ентов.

Неявная схема с опережением имеет первый порядок точности

по времени, что приводит в ряде случаев к значительной погрешно-

сти. Величину погрешности можно существенно уменьшить, приме-

нив симметричную схему, записываемую в виде

Дt

hx h

, /Г+/1

l</<iV-l. (3.79)

Пространственная производная этого уравнения аппроксимирована

со вторым порядком точности (3.17). Оценим порядок точности вре-

менной производной. Для этого представим уравнение (3.79) в виде

(3.80)

0,5(£/Й

) ~ 2-0,5(и'+

т)

0,5(и'?-\

ии)

0,5(fJ + f1

)

Значения искомой функции, записываемые в виде 0,5(f/|

+ £/•),

можно рассматривать как средние на интервале [м + 1)], т.е. в момент

времени t + т/2.

Разложим функции £/|

и и\ в ряд Тейлора по временной коор-

динате в окрестности точки и

(+0,5

'dl/Л

v dt J

t+0t5

+ -

v2y

1 (т

Ч У

lfx^-

612

ч^

+ -

У/+о,5

эи

Э;

612

+ ...; (3.81)

+ ... (3.82)

Вычтем из первого выражения второе и поделим на т:

иТ

~и\

(Щ

д t

//+0,5

3 8

V y

f+0

-к..

(3.83)

Таким образом, исходное уравнение (3.79) обеспечивает второй

порядок точности и по временной координате. Преобразуя указанное

выражение для всех внутренних точек исследуемой области, полу-

чим трёхчленную систему алгебраических уравнений, правая часть

которых имеет более сложную структуру, а коэффициенты

_ htkj. _ h,kj, _

й/Ь ,

~2h

~ 2hV

\|m +

(f/;-.

f/;+.)

+ 0,5ft

(Fl + Fr

)- (3.84)

Краевые и начальные условия при этом сохраняются. Полученная сис-

тема трёхчленных алгебраических уравнений решается описанным

выше методом прогонки с минимальными временными затратами.

Пример 3.3. Решение смешанной краевой задачи. На интерва-

ле [0,0,6] решить краевую задачу, описываемую уравнением [28]

ди _ д

dt дх

при следующих начальных и краевых условиях

[/(0,0 = 2(f + 0,06); U(L,t) = 0,84; t/(x,0) = 3x(l-x) + 0,12.

Решение задачи с использованием явной схемы. Разобьём иссле-

дуемую область [0, 0,6] на 6 интервалов величиной h

= 0,1. Аппрок-

симируем дифференциальные операторы конечно-разностными вы-

ражениями и, выполнив преобразования, получим

U'^-U'i

M-2Ui + UU

ht hi

Выберем величину временного интервала из условия устойчивости

счёта: \ < 0,5h

. Примем с запасом А, =0,0025.

Подставляя h

и h, в полученное уравнение и выполняя преоб-

разования, будем иметь

и;*

= 0,25 и'

+ 0,5*/; + 0,25 и и.

Начальные значения функции в исследуемой области рассчиты-

ваем для всех интервалов разбиения пространственной координаты

в соответствии с заданной функцией

U? = 3/у(1 - hj), i = 1,2,..., N -1.

Краевые значения на левой границе для времени 0<t<t

рас-

считываются по выражению

Uo = 2(hJ + 0,06),

а на правой границе принимаются U'n = 0,84 .

Рассчитываются по формуле значения искомой функции и'*

для

момента времени t и пространственной координаты х, начиная с мо-

мента времени t = 0.

Программа решения краевой задачи с использованием явной

схемы:

nx=7; nt=9; hx=0.1; ht=0.0025;

for

j=l:nx

x=hx*(j-l); u( 1 ,j )=3. * x* (1. -x)+0.12;

end

fort=l:nt

u(t,

1 )=2. *(ht*(t-1 )+0.06); u(t,nx)=0.84;

end

for t=l:nt-l

for j=2:nx-l

u(t+l,j)=u(t,j)+ht*(u(tj+l)-2.*u(t,j)+u(tj-l))/(hx*hx);

end

disp(u);

Результаты решения приведены в табл. 3.5.

Таблица 3.5

Результаты решения краевой задачи с использованием

явной схемы

Время

Пространственная координата

Время

0 0,1

0,2

0,3

0,4 0,5 0,6

0,12 0,39

0,6000 0,7500 0,8400

0,8700

0,84

0,0025 0,1250

0,3750

0,5850 0,7350

0,8250

0,8550 0,84

0,005

0,1300

0,3650

0,5700 0,7200 0,8100

0,8438 0,84

0,0075

0,1350

0,3575

0,5563 0,7050

0,7959

0,7959 0,84

0,01

0,1400 0,3516

0,5438 0,6905 0,7828

0,8262 0,84

0,0125 0,1450 0,3467

0,5324 0,6769 0,7706 0,8188

0,84

0,015

0,1500 0,3427

0,3427 0,6642 0,7592

0,8120 0,84

0,0175 0,1550

0,3394

0,5128

0,6524

0,7487

0,84

0,02

0,1600

0,3366

0,5043 0,6416 0,7389

0,8001

0,84

Решение краевой задачи для неявной схемы с опережением.

Аппроксимируем дифференциальные операторы уравнения сле-

дующим образом:

h, hi

и преобразуем полученное выражение к виду

AiU

й - CiUT

+ BiU'itl

= ~Fi, i = l, 2,...,N-1,

где Д. =h,/hl; В, =h,/hl; С, =l + 2/i,/^

; F

= U\.

Полученная система трёхчленных алгебраических уравнений

решается методом прогонки. Недостающие до определения системы

уравнения записываются исходя из краевых условий. Для определе-

ния правой части уравнений на первом временном интервале исполь-

зуются начальные условия, а на последующих интервалах - полу-

ченные ранее решения.

Программа расчёта приведена ниже, а результаты решения

краевой задачи, полученные с использованием неявной схемы с опе-

режением, представлены в табл. 3.6.

Программа решения краевой задачи:

nx=6; t=0; tk=0.0225; ht=0.0025; hx=0.1;

for

j=l:nx+l

x=hx*(j-l); u0(j)=3.*x*(l.-x)+0.12;

end

disp(uO); t=t+ht;

for

j=l:nx

a(j)=ht/hx

2; b(j)=a(j); c(j)=l.+2.*ht/hx

end

while t<tk

u(l)=2.*(t+0.06); alf(2)=0.; bet(2)=u(l);

for

j=2:nx

r=c(j)-aO)*alf(j); alf(j+l)=b(j)/r; bet(j+l)=(uOG)+a(j)*betG))/r;

end

u(nx+l)=0.84;

for

j=nx:-l:2

u(j)=alf(j+1) *u(j+1 )+bet(j+1);

end

disp(u); u0(2: nx)=u(2: nx); t=t+ht;

end

Таблица 3.6

Результаты решения краевой задачи для неявной схемы

с опережением

Время

Пространственная координата

Время

0,1

0,2 0,3

0,4

0,5

0,6

0,1200

0,3900

0,6000 0,7500 0,8400

0,8700 0,8400

0,0025 0,1250 0,3784

0,5856

0,7352

0,8255

0,8576

0,8400

0,005 0,1300 0,3693

0,5721

0,7207 0,8116 0,8470

0,8400

0,0075 0,1350

0,3620

0,5595 0,7068 0,7985

0,8377 0,8400

0,01 0,1400 0,3560 0,5479 0,6936

0,7862

0,8295

0,8400

0,0125 0,1450

0,3510

0,5373

0,6810

0,7746 0,8221

0,8400

0,015

0,1500

0,3469

0,5276 0,6693 0,7639 0,8154

0,8153

0,0175 0,1550 0,3438 0,5187 0,6583 0,7538 0,8092

0,8400

0,02 0,1600

0,3408

0,5106 0,6480 0,7445 0,8036

0,8400

Решение краевой задачи с использованием симметричной неяв-

ной схемы. Дифференциальные операторы уравнения аппроксими-

руются в этом случае следующим образом:

к ' к ' h

Преобразовывая полученное выражение, снова получим систему

трёхчленных алгебраических уравнений, коэффициенты которой за-

писываются в следующем виде:

Л=Л,/(2Л,

);

l(2hl\, С,- =

+ ft, //г

;

U-

2U>

^)-

Программа решения краевой задачи с использованием симмет-

ричной неявной схемы:

nx=6; t—0; tk=0.0225; ht=0.0025; hx=0.1;

for j=l:nx+l

x=hx*G-l); u0(j)=3.*x*(l.-x)+0.12;

end

disp(uO);

t=t+ht;

for j=l:nx

a(j)=ht/(2.

*hx

2);

b(j)=a(j); c(j)=l.+2 *ht/(2.*hx

2);

end

while tctk

u(l)=2.*(t+0.06); alf(2)=0.; bet(2)=u(l);

for

j=2:nx

r=c(j)-a(j)*alf(j); alfG+l)=bG)/r;

f=uO(j)+ht*(uO(j+1

)-2.

*uO(j)+uO(j-1 ))/(2. *hx

2);

bet(j+ l)=(f+a(j)*bet(j))/r;

end

u(nx+l)=0.84;

for

j=nx:

-1:2

u(j)=alf(j+ l)*u(j+ l)+bet(J+l);

end

disp(u);

u0(2

:nx)=u(2:

nx);

t=t+ht;

end

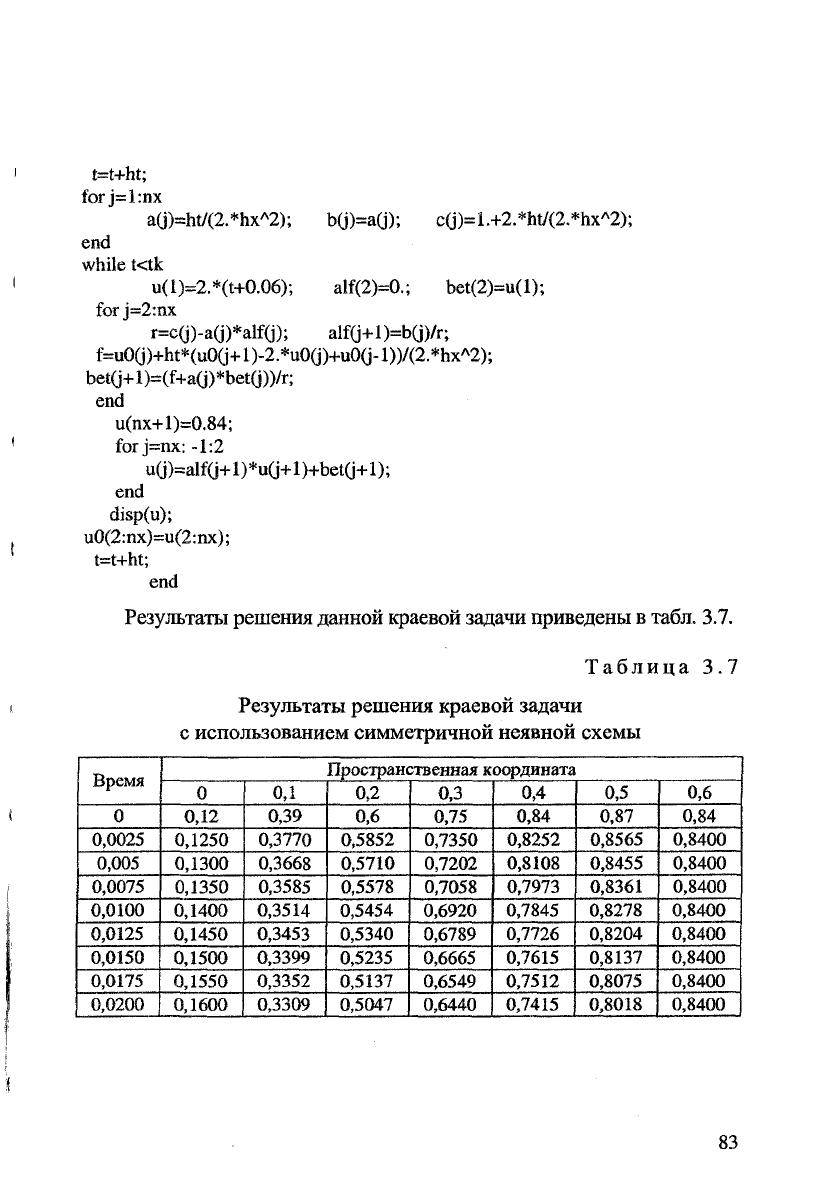
Результаты решения данной краевой задачи приведены

табл.

3.7.

Таблица

3.7

Результаты решения краевой задачи

использованием симметричной неявной схемы

Время

Пространственная координата

Время

0 0,1

0,2

0,3

0,4 0,5 0,6

0 0,12

0,39

0,6 0,75 0,84 0,87 0,84

0,0025

0,1250

0,3770

0,5852

0,7350

0,8252

0,8565

0,8400

0,005

0,1300

0,3668

0,5710

0,7202

0,8108 0,8455

0,8400

0,0075

0,1350

0,3585

0,5578 0,7058

0,7973 0,8361 0,8400

0,0100

0,1400

0,3514

0,5454

0,6920 0,7845

0,8278 0,8400

0,0125

0,1450

0,3453

0,5340

0,6789

0,7726

0,8204 0,8400

0,0150

0,1500

0,3399

0,5235 0,6665

0,7615 0,8137 0,8400

0,0175

0,1550 0,3352 0,5137 0,6549 0,7512 0,8075 0,8400

0,0200

0,1600 0,3309

0,5047

0,6440

0,7415 0,8018 0,8400

Сравнение рассмотренных вариантов показывает, что они обла-

дают практически одинаковой точностью, но наиболее простой

в реализации оказывается явная схема. К сожалению, эта схема явля-

ется условно устойчивой, т.е. даёт правильное решение при опреде-

лённых соотношениях между пространственным и временным ин-

тервалами согласно (3.78).

Рассмотрим характер протекания переходного процесса при ре-

шении нестационарной одномерной краевой задачи при различных

соотношениях между указанными интервалами.

Пример 3.4. Решение смешанной краевой задачи с использова-

нием явной схемы при различных величинах временного интервала.

Пусть краевая задача на интервале [0, 1] описана уравнением парабо-

лического типа

ди д

—

-r-r

f(x) (3.85)

at д

с нулевыми начальными и граничными условиями

£/(0, t)

U(l t)

U(x,0)

При решении смешанной задачи с использованием явной схемы

получаем следующее уравнение:

= и; +~(и'

- 2 и; + + /А

)

(3.86)

где г-временной;

- пространственный интервалы, h = 0,1.

Для устойчивости решения рассматриваемой краевой задачи

при величине пространственного интервала h

= 0,1

величина вре-

менного интервала согласно (3.78) не должна превышать

< —= 0,005.