Беляев Е.Ф., Шулаков Н.В., Дискретно-полевые модели электрических машин, учебное пособие

Подождите немного. Документ загружается.

или

ДФ -——ДФ, = -F

, (3.27)

или

ЯмЛ-^ЛФ (3-28)

В этих уравнениях:

- МДС, создаваемая сторонними токами

на исследуемом г'-м интервале; Ду - величина пространственного

интервала по оси у; ЛФ

и ДФ

- приращения магнитных потоков

по соответствующим координатным осям при протекании сторонних

токов;

и S

- поверхности, по которым протекают магнитные по-

токи ДФ^и ДФ.; R

и - магнитные сопротивления соответст-

вующих участков магнитной цепи.

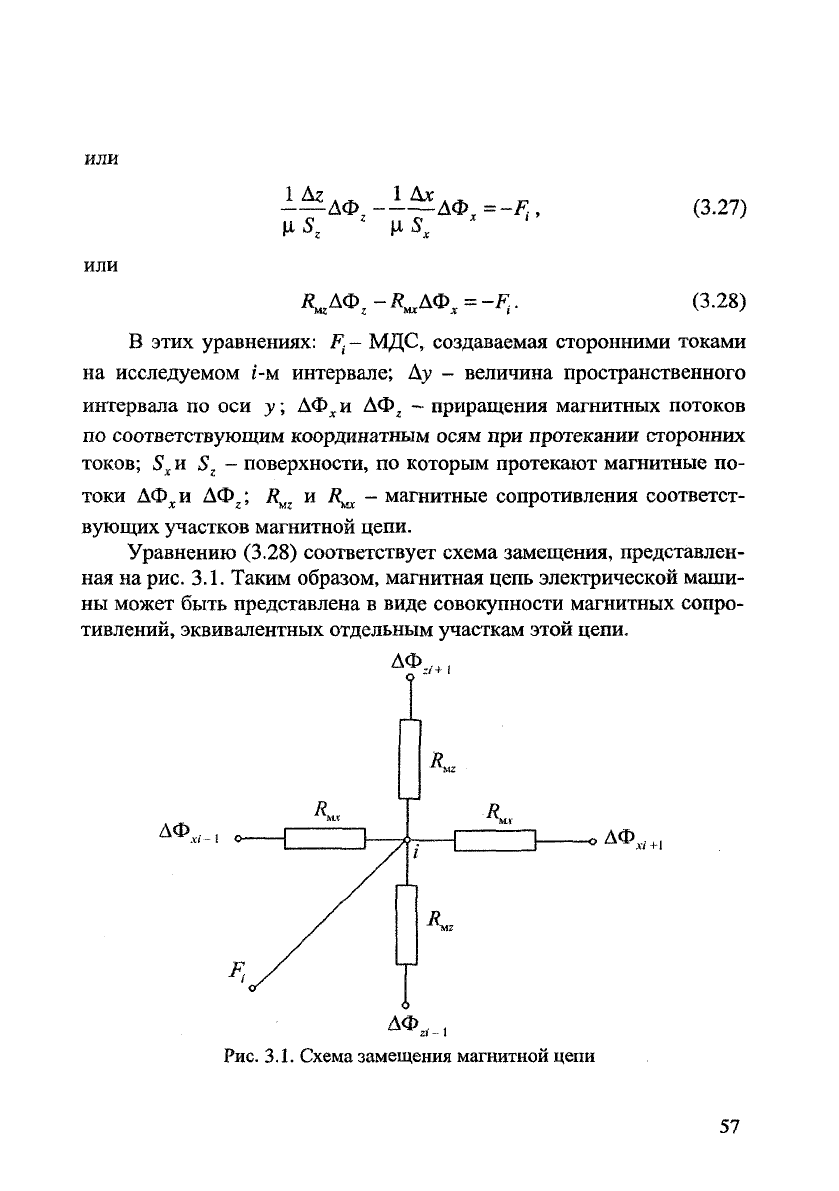
Уравнению (3.28) соответствует схема замещения, представлен-

ная на рис. 3.1. Таким образом, магнитная цепь электрической маши-

ны может быть представлена в виде совокупности магнитных сопро-

тивлений, эквивалентных отдельным участкам этой цепи.

Рис. 3.1. Схема замещения магнитной цепи

Электромагнитные процессы магнитной цепи описываются

уравнениями Кирхгофа для отдельных её участков, и решение по-

лученной системы уравнений позволяет определить магнитные по-

токи и соответствующие индукции этих участков.

3.2. РЕШЕНИЕ СИСТЕМЫ АЛГЕБРАИЧЕСКИХ

УРАВНЕНИЙ МЕТОДОМ ПРОГОНКИ

3.2.1. Простая прогонка

Для решения системы алгебраических уравнений, полученной

в результате аппроксимации дифференциальных операторов, могут

быть использованы различные методы. Однако на практике наиболее

часто используются специальные методы решения, учитывающие

структуру полученной системы. К таким методам относится рас-

сматриваемый ниже метод прогонки [24, 27].

Положим, что в области [0,L] решается краевая задача с гранич-

ными условиями первого рода:

и ди

АГ,

-F(x) ; (3.29)

дх

U(0)

= a;

U (L)

Ь.

Будем решать задачу конечно-разностным методом. Для этого ис-

следуемую область [0,/,] разбиваем на конечное число интервалов N

величиной Ax

L/N и дифференциальные операторы аппроксимируем

конечно-разностными выражениями. В результате замены получим сис-

тему алгебраических уравнений

-Щ+

£/,-,

-и^

ки =

(Axf ' 2Ах

— 1,

2 N-l. (3.30)

Преобразовывая уравнения системы, запишем их в виде

-K

Ax)Ut-i~\2

(Дх)

]{/,. +(l

Ax)u

-F

(Дxf.

(3.31)

Обозначим:

Д. =

- К, Дх; В, =1+ К, Дх; С, = 2 +

(д*)

;

/, = ^(д*)

. (3.32)

Граничные условия в общем виде записываются как:

UN=X

UN-I+P

. (з.зз)

При Xi = 0 и х

= 0 имеем граничные условия первого рода, при

Xi =

и х

-1 - граничные условия второго рода, в противном слу-

чае - условия третьего рода. Таким образом, рассматриваемая крае-

вая задача может быть записана следующим образом:

Л,С/

- СД + Д,.£/

(+1

= -/., i = l,2 N-2,N-l-, (3.34)

tf* =x

£Vi +

P-

> »

Указанная система является определённой, так как число неиз-

вестных равно числу уравнений. Для её решения чаще всего использу-

ется разновидность метода Гаусса- метод прогонки. Рассмотрим

идею этого способа. Положим, что решение системы можно записать

в виде

Ui = ш+iUi+i +

Pf+i >

(3.35)

коэффициенты которого a,+i и р

(+1

необходимо определить. Для точ-

ки i справедливо соотношение £/

= a,£/, + Р,- Подставляя это вы-

ражение в уравнение системы, получим

Электромагнитные процессы магнитной цепи описываются

уравнениями Кирхгофа для отдельных её участков, и решение по-

лученной системы уравнений позволяет определить магнитные по-

токи и соответствующие индукции этих участков.

Для решения системы алгебраических уравнений, полученной

в результате аппроксимации дифференциальных операторов, могут

быть использованы различные методы. Однако на практике наиболее

часто используются специальные методы решения, учитывающие

структуру полученной системы. К таким методам относится рас-

сматриваемый ниже метод прогонки [24, 27].

Положим, что в области [0,L] решается краевая задача с гранич-

ными условиями первого рода:

Будем решать задачу конечно-разностным методом. Для этого ис-

следуемую область

[О, L]

разбиваем на конечное число интервалов N

величиной Ах

L/N и дифференциальные операторы аппроксимируем

конечно-разностными выражениями. В результате замены получим сис-

тему алгебраических уравнений

3.2. РЕШЕНИЕ СИСТЕМЫ АЛГЕБРАИЧЕСКИХ

УРАВНЕНИЙ МЕТОДОМ ПРОГОНКИ

3.2.1. Простая прогонка

и ди

+ к

2U =

f(x)

'х

' дх

(3.29)

U(0)

= a;

U(L)-b.

(Ах)

2Ах

l, 2,..., N -I.

(3.30)

Преобразовывая уравнения системы, запишем их в виде

- К

Ах)и^ ~[2

(Ax)

]t/,. +

+ К^х)и

-F

( Дх)

. (3.31)

Обозначим:

Д =

- К

Дх; В, = 1+ ^Дх; С, = 2 + ^(Дх)

;

(

= ^(Дх)

. (3.32)

Граничные условия в общем виде записываются как:

i7o=X,i/i + p

; UN = X

UN-i + p

- (3.33)

При Xi

Хг

0 имеем граничные условия первого рода, при

и х

~ граничные условия второго рода, в противном слу-

чае - условия третьего рода. Таким образом, рассматриваемая крае-

вая задача может быть записана следующим образом:

C/o=XiC, +

Hi>

г=0

AJU

-СД. + 0,1/

= -/„

= 1,2,..., А^-2,iV-l; (3.34)

„

l + i

, i

Указанная система является определённой, так как число неиз-

вестных равно числу уравнений. Для её решения чаще всего использу-

ется разновидность метода Гаусса- метод прогонки. Рассмотрим

идею этого способа. Положим, что решение системы можно записать

в виде

Ui - ш+iUf+i + Pi+i. (3.35)

коэффициенты которого a,+i и

1+1

необходимо определить. Для точ-

ки i справедливо соотношение £/

= «;£/, +Р,- Подставляя это вы-

ражение в уравнение системы, получим

А,(а,г/

+ Р,.)~С,г/« + B,Um = -fi (3-36)

или

(А,а, - C,)U,+

А.Р,-

+ BiV

= -/,. (3.37)

Аналогично, подставляя вместо {/,• выражение (3.35) и выпол-

няя промежуточные преобразования, будем иметь

[А

(А,а,-

~CI)

B^UM + ( AM, ~ C,)P

i + А,Р

= -/,

•

(3.38)

Это уравнение будет справедливо, если выполнены условия:

a,+i(Aia,

Ci)+ Bi = 0; (3.39)

(

C;)P

i + Л, P + /, = 0. (3.40)

Отсюда следуют выражения для a

i и P

i+1

a.+i =

; P

i+I

Р + /

' • i = 1, 2, ..., ЛМ. (3.41)

C, ~ a, А/ С, ~ a,A,

Полученные выражения носят название рекуррентных и позволя-

ют, зная начальные значения величин а, и Р

(

, рассчитать все после-

дующие. Выражения для начальных значений

, и р. можно найти,

исходя из граничных условий (3.33). Для i = 0 имеем, с одной стороны,

а с другой, согласно (3.35), -

Соотношения будут выполнены, если ai = Xi

Mi •

Таким об-

разом, при известных граничных условиях определяются прогоноч-

ные коэффициенты щ. Р,, а затем а, и (3, для i = 2,3,..., N -I (пря-

мой ход). Величина искомой функции на последнем пространствен-

ном интервале при i = N определяется из граничных условий в этой

точке. С одной стороны,

-l

а с другой, по выражению (3.35), -

UN-\ =

CLNUN

РДГ

•

Из этой системы находится значение функции на последнем ин-

тервале разбиения пространственной координаты:

(3.42)

awX

Зная эту величину и используя выражение (3.35), можно рассчи-

тать значения искомой функции на остальных интервалах разбиения

I = N -1, N - 2,...,

(обратный ход).

Используя этот метод, необходимо выполнить определённые

условия, обеспечивающие устойчивость вычислительного процесса:

первое условие

|с,|>|л,| + |в,|,

= 1,2,...,N-l, (3.43)

причём строгое неравенство должно выполняться хотя бы в одной

точке;

второе условие

|Х,|

+ |Х

|<2. (3.44)

При выполнении этих условий знаменатель выражений (3.41)

всегда больше числителя и величина коэффициентов а, оказывается

всегда меньше единицы. Поэтому возникшие в процессе расчёта

ошибки округления не приводят к их возрастанию и накоплению.

Достоинством метода является минимальное число математиче-

ских операций, необходимых на его реализацию и, самое главное,

линейная зависимость числа операций от числа алгебраических

уравнений (порядка 10 операций). Такие методы принято называть

экономичными [24]. Это обстоятельство делает метод прогонки весь-

ма популярным для решения уравнений математической физики.

Помимо основного варианта метода прогонки разработаны раз-

новидности, применяемые для решения тех же краевых задач, что

и для основного варианта. К ним относятся метод обратной прогонки

и метод встречных прогонок.

Как следует из названия, метод обратной прогонки отличается

тем, что вычисление прогоночных коэффициентов т], и q

произво-

дится в обратной последовательности, начиная с iV-интервала для

А' -1, N -2, ...,2,1, с использованием выражения (3.35), а вычисле-

ние функции в прямой последовательности

2,..., N - 2, N -1:

Uш =

<;,,

i = l,2,...,iV-l. (3.45)

Метод встречных прогонок применяется в том случае, если не-

обходимо найти решение в одной из точек исследуемой области. Для

этого, исходя из граничных условий при

= 0, рассчитывают прого-

ночные коэффициенты а; и р

, до исследуемой точки. Затем рассчи-

тываются прогоночные коэффициенты т|. и c

, исходя из граничных

условий на второй границе при i = N . Записываются выражения ис-

комой величины в исследуемой точке:

Ui = a

+ P

'> UM = i\fJ, + q,. (3.46)

Совместное решение этой системы позволяет определить значе-

ние искомой функции в точках i и i +1. При необходимости значе-

ния функции в других точках исследуемой области рассчитываются

по любому из приведённых выражений (3.46). Для реализации мето-

да здесь и далее использован пакет MATLAB [29].

Пример 3.1. Решение краевой задачи методом прогонки. На ин-

тервале [0,1] решим краевую задачу методом прогонки:

Y"-2XY'-2Y = -4X\ Г(0) - Г(0) = 0; F(l) =

= 3,71828,

и сравним решение, полученное численным методом, с аналитиче-

ским решением [28]

Г = Х+ехр(х

Для решения задачи исследуемую область разбиваем на N -10

интервалов величиной

^ = 1/^ =

1/10

= 0,1.

Дифференциальные операторы уравнения заменяем конечно-

разностными выражениями:

Y - 2Y + Y Y -Y.

ii±i -

2Z,.

2Y,

= -АХ..

hi '2 К

Преобразуя эти выражения, получим систему трёхчленных ал-

гебраических уравнений для каждого из интервалов разбиения про-

странственной координаты:

=-F

с коэффициентами

Д. =

+ X

; 5,= 1-ХД; С,=2 + 2й*, i = l,2,..., JV-2,iV-l, JV.

Краевые условия аппроксимированы следующим образом:

o-(Yi~

o)^K =°; =3,71828.

Отсюда

у 1

Прогоночные коэффициенты

1 о

я Zi+Mi.

l +

Тг*

Ci~a.iAi С,-а,Л,

i = l, 2,...,N-\.

Записываем значение искомой функции на каждом интервале

разбиения пространственной координаты

Yi = (XMYM + 3

i+I

; i = N-l, N-2,...,2,1.

Программа решения краевой задачи:

n=10; hx=l./n;

for

j=l:n

x(j)=hx*j; a(j)=l.+x(j)*hx; b(j)=l.-x(j)*hx; c(j)=2.+2.*hx

2; f<j)=4.*x(j)*hx

end

alf(2)=l./(l.+hx); bet(2)=0.;

for j=2: n

rl=c(j)-a(j)*alf(j); alf(j+l)=b(J)/rl; bet(j+l)=(a(j)*betCj)+f(j»/r 1;

end

y(n+l)=3.71828;

for

j=n:-l:l

y(j)=alf(j+l)*y(j+l)+bet(j+l);

end

for

j=l:n+l

x(j)=hx*(j-l); xl=x(j)

2; x3=exp(xl); xx(j)=xG)+x3;

end

disp(y); disp(xx);

Результаты расчета приведены в табл. 3.1, 3.2.

Таблица 3.1

Коэффициенты системы трёхчленных алгебраических уравнений

в зависимости от пространственной координаты

X Ai Bi

0,10000

1,0100 0,9900

2,0200 0,0040

0,20000

1,0200

0,9900 2,0200 0,0080

0,30000

1,0300

0,9700 2,0200 0,0120

0,40000 1,0400 0,9600

2,0200 0,0160

0,50000

1,0500

0,9500 2,0200 0,0200

0,60000

1,0600

0,9400 2,0200 0,0240

0,70000 1,0700 0,9300

2,0200 0,0280

0,80000 1,0800 0,9200

2,0200 0,0320

0,90000 1,0900

0,9100 2,0200 0,0360

1,00000 1,1000

0,9000

2,0200

0,0360