Беляев Е.Ф., Шулаков Н.В., Дискретно-полевые модели электрических машин, учебное пособие

Подождите немного. Документ загружается.

скими выражениями. Амплитуда и фаза каждой из гармоник иссле-

дуемой величины в этом случае рассчитываются через соответст-

вующие параметры токовой нагрузки и параметры ЭМ при помощи

простейших алгебраических выражений. Необходимость решения

дифференциальных уравнений в этом случае отпадает, так как пото-

косцепления машины легко выражаются через её фазные токи.

Для нестационарных режимов дифференциальные уравнения для

каждой из пространственных гармоник магнитного поля записывают-

ся в виде обыкновенных дифференциальных уравнений с временной

независимой переменной. Таким образом, зная гармонический состав

токовой нагрузки статора, можно всегда определить соответствующие

потокосцепления, рассчитать индуктивности обмоток и, воспользо-

вавшись системой уравнений Кирхгофа, рассчитать динамический ре-

жим работы ЭМ. На этом этапе были получены весьма важные резуль-

таты, позволяющие судить как о свойствах самих ЭМ, так и систем,

включающих ЭМ в свой состав.

Недостатком математических моделей, построенных на основе

электрических цепей, является необходимость иметь известными па-

раметры схем замещения, которые определяются либо в процессе

эксперимента, либо путём дополнительных расчётов, либо прибли-

жённо на основании практического опыта. Другим недостатком этих

моделей является невозможность нахождения в процессе моделиро-

вания дифференциальных параметров, таких как магнитная индукция

в элементах магнитопровода ЭМ, плотности распределения электро-

магнитных потерь, определяющих нагрев отдельных частей машины

и т.д. При моделировании в данном случае используются и рассчи-

тываются интегральные величины: магнитные потоки, токи, ЭДС,

мощности и т.п.

Более совершенными являются современные методы математи-

ческого моделирования, основанные на решении уравнений электро-

магнитного поля ЭМ [22, 30, 32, 33]. При таком подходе область су-

ществования этих полей рассматривается как сплошная среда, обла-

дающая определёнными магнитными и электрическими свойствами.

Если в каждой точке исследуемой области задано значение физиче-

ской величины, то говорят, что задано поле этой физической величи-

ны. Следовательно, исследование магнитных и электрических полей

связано с определением значений этих величин в каждой точке ис-

следуемой области.

Эти методы не требуют знания параметров ЭМ, более того, они

могут быть рассчитаны в процессе моделирования по результатам

расчётов магнитных и электрических полей. Для моделирования

электромагнитных процессов необходимо иметь пространственное

распределение магнитных и электрических свойств элементов ЭМ.

По результатам расчёта магнитных и электрических полей могут

быть определены дифференциальные параметры машины, простран-

ственное интегрирование которых позволяет легко рассчитать инте-

гральные величины, определяющие свойства ЭМ.

Недостатком этого способа математического моделирования яв-

ляется его трудоёмкость, обусловленная сложностью решения сис-

тем уравнений в частных производных. Правда, бурное развитие вы-

числительной техники и методов вычислений значительно ослабляет

этот недостаток.

. Современные методы математического моделирования откры-

вают широкие возможности не только для исследования сущест-

вующих ЭМ, но и весьма перспективны для проектирования новых

конструкций ЭМ и их оптимизации путём варьирования геометриче-

ских размеров и физических свойств используемых материалов. Тем

не менее представляется целесообразным сочетать оба способа моде-

лирования ЭМ, используя схемы замещения для участков, незначи-

тельно влияющих на свойства и характеристики машин, и детально

исследуя электромагнитные поля, определяющие основные характе-

ристики и показатели ЭМ.

Разработка математических моделей ЭМ оказалась бы невозмож-

ной без фундаментальной научной базы, представленной трудами

иностранных учёных: Р. Рюденберга, К. Адкинсона, Г. Вудсона,

В. Гиббса, Э. Кларка, К. Ковача, Г. Крона, В. Лайона, Р. Парка, Р. Рих-

тера, Г. Стэнли, Д. Уайта и многих других.

Большой вклад в разработку математической теории и построе-

ние математических моделей внесли отечественные учёные:

Г.Н. Петров, М.П. Костенко, Л.М. Пиотровский, А.А. Горев, А.И. Воль-

дек, Е.Я. Казовский, А.И. Важное, М.М. Соколов, И.А. Глебов,

И.П. Копылов, А.В. Иванов-Смоленский, Я.Б. Данилевич, Г.А. Сипай-

лов, А.А. Янко-Триницкий, В.Я. Беспалов, К.С. Демирчян, Е.В. Коно-

ненко, Е.М. Синельников, Н.С. Сиунов, Р.В. Фильц, В.В. Хрущёв,

И.М. Серый, Ф.Н. Сарапулов, А.Т. Пластун и многие другие.

Математическая теория специальных ЭМ создана отечественными

и иностранными учёными, среди них: А.И. Вольдек, Г.И. Штурман,

Б.И. Петленко, Ф.Н. Сарапулов, М.Г. Резин, А.П. Ращепкин, Е.М. Огар-

ков, Х.А. Тийсмус, Е.Р. Лайтвайт, С.А. Насар, К. Оберретль, И.С. Са-

боннадье, С. Ямамура и другие.

Создали теоретические положения и разработали математиче-

ские модели на основе теории электромагнитного поля в своих

трудах И.П. Копылов, А.В. Иванов-Смоленский, В.Я. Беспалов,

Г.А. Сипайлов, К.А. Хорьков, Я.Б. Данилевич, В.В. Домбровский,

К.С. Демирчян, О.В. Тозони, Ф.Н. Сарапулов, А.А. Пульников,

а также иностранные учёные Е. Andutsen, Н.А. Anwari, J.P. Bastos,

R. Goyet, S. Car, W. Kunze, А. В inner и многие другие.

Часть I

ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЁТА МАГНИТНЫХ ПОЛЕЙ

1. МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

1.1. МАТЕМАТИЧЕСКИЕ ФУНКЦИИ

Наряду с хорошо известными и широко применяемыми на прак-

тике аналитическими функциями при математическом моделирова-

нии эффективно использование некоторых специальных математиче-

ских функций. Для описания магнитных полей и электромагнитных

процессов ЭМ чаще всего будут использованы следующие матема-

тические функции [12].

Периодические временные и пространственные функции - это

функции, значения которых повторяются через определённый вре-

менной промежуток Т или пространственный интервал L, называе-

мые периодом:

F(t)

F(t

Т) ; F(x)

F(x

L). (1.1)

Периодические временные функции получили широкое распро-

странение для исследования электрических цепей переменного тока.

Периодические пространственные функции используются для мате-

матического описания пространственных распределений магнитных

полей в круговых машинах.

Финитные функции - это функции, значения которых отличны

от нуля лишь на определённых интервалах:

F(x)

0 на интервале [а,b], (1.2)

Финитные функции широко применяются для описания магнит-

ных полей, затухающих в пространстве. В качестве примера исполь-

зования финитной функции можно привести математическое описа-

ние распределения магнитного поля ЭМ вдоль её оси, затухающего

при удалении от магнитопровода. На некотором расстоянии (теоре-

тически равном бесконечности) от магнитпровода магнитное поле

машины можно считать затухшим. Говорят, что в этом случае носи-

телем финитной функции является вся числовая ось. В реальных ус-

ловиях магнитное поле можно считать затухшим на расстоянии, рав-

ном величине десяти воздушных зазоров. Поэтому носителем будет

являться интервал конечной величины.

При решении краевых задач, связанных с расчётами магнитного

поля, широкое распространение получили следующие функции.

Единичная функция Хевисайда, которая определяется следую-

щим образом (рис. 1.1):

Е(х) =

0 при лг<0,

— при х~0,

1 при х>0.

(1-3)

Единичная функция может быть записана для любой точки циф-

ровой оси:

jЕ(Х —

—

0 при л:<х

- при x = x

1 при х>х

(1.4)

Е(х)

Ф 1.0

Хо

Рис. 1.1. Единичная функция Хевисайда

Единичные функции Хевисайда удобны для описания кусочно-

непрерывных функций пространственных координат. Примером ис-

пользования единичных функций является математическое выражение

для электропроводности проводника ограниченной длины в функции

пространственной координаты (рис. 1.2). Математическая запись этой

функции выглядит следующим образом:

У(*)

у\Е(х - х,) - Е(х - х, ]. (1.5)

При х<Лу у(х) = 0; при х, <х<х, у(

)

у-0

у; при х>х

7(х) = у -

= 0.

у/\

X J Х2 X

Рис. 1.2. Графическое изображение электропроводности

в функции пространственной координаты

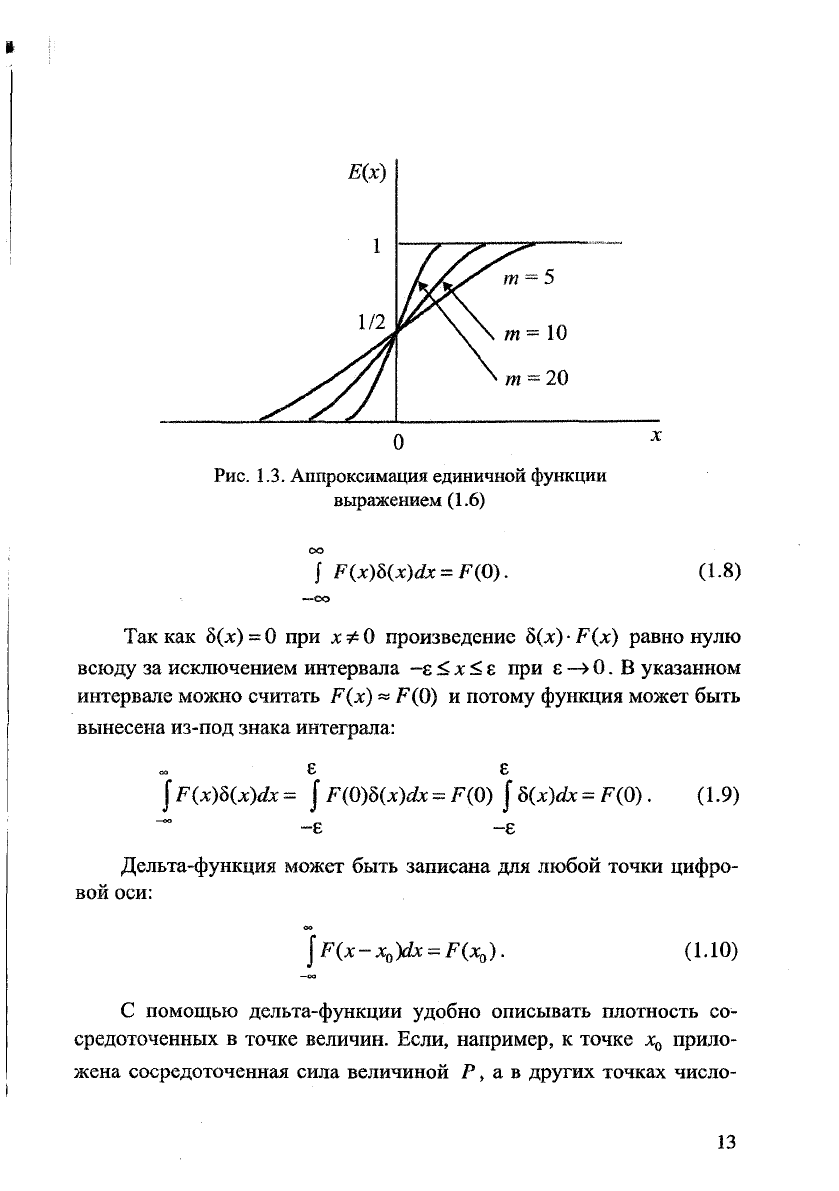
Единичная функция Хевисайда может быть аппроксимирована

с определённой точностью непрерывными математическими функ-

циями, например:

1 1

Е(х) =

—

+ —arctg(mx) при т—(1.6)

2 к

Если х

—>

—°°, то

arctg(тх)

-» -я/2. В этом случае Е(х)

—>

Если х = 0, то arctg(mx) = 0 и Е(х) = 1/2. Если х

—»

«>, то

arctg(mx)

—»

л/2 и £(х)

—>

1. График функции (1.6) показан на

рис.

1.3.

Дельта-функция Дирака может быть представлена выражениями:

5(*)J~ "

РИ Л = 0

' (1.7)

10 при хФ 0.

J 5(x)dx

Дельта-функция обладает фильтрующим свойством:

Е(х)

1 1

LZ/r т

= 5

1/2

\ \ т

= 10

^ т

= 20

Рис. 1.3. Аппроксимация единичной функции

выражением (1.6)

со

s F(x)8(x)dx

F(0). (1.8)

—со

Так как 6(х) = 0 при х&О произведение 8(х)

•

F(x) равно нулю

всюду за исключением интервала -s < х < е при е

—>

0. В указанном

интервале можно считать F(x) ~ F(0) и потому функция может быть

вынесена из-под знака интеграла:

е е

fF(x)8(x)dx

{ F(0)8(x)dx

F(0) f 8(x)dx

F(0). (1.9)

-e -e

Дельта-функция может быть записана для любой точки цифро-

вой оси:

= (1.10)

С помощью дельта-функции удобно описывать плотность со-

средоточенных в точке величин. Если, например, к точке х

прило-

жена сосредоточенная сила величиной Р, а в других точках число-

вой оси сила отсутствует, то плотность силы в функции пространст-

венной координаты q{x) может быть записана в виде

q{x) =

/> •

8 (л - х

). (1.11)

При расчётах магнитных полей часто используется величина AS,

называемая линейной плотностью тока. Под этой величиной обычно

подразумевают суммарный ток, сосредоточенный в узком слое на по-

верхности магнитопровода с координатой z

. Линейную плотность то-

ка в этом случае можно записать следующим образом:

AS(z)

AS-8(z-z

). (1.12)

Дельта-функция может быть аппроксимирована различными ана-

литическими функциями, например:

8(х) =

—

- при ш

—>

°°. (1.13)

+ Отг)

Если х

0, то 8(л) 0. Если, наоборот, х = 0, то

с/ ч

5(х) —> — =

оо .

Дельта-функция связана с единичной функцией Хевисайда сле-

дующей зависимостью:

5(х) =

^ВД (1.14)

и, наоборот,

Е(х) = J b(x)dx. (1.15)

—оо

Действительно, в точке разрыва производная функции обраща-

ется в бесконечность, т.е. возникает импульсная функция (рис. 1.4).

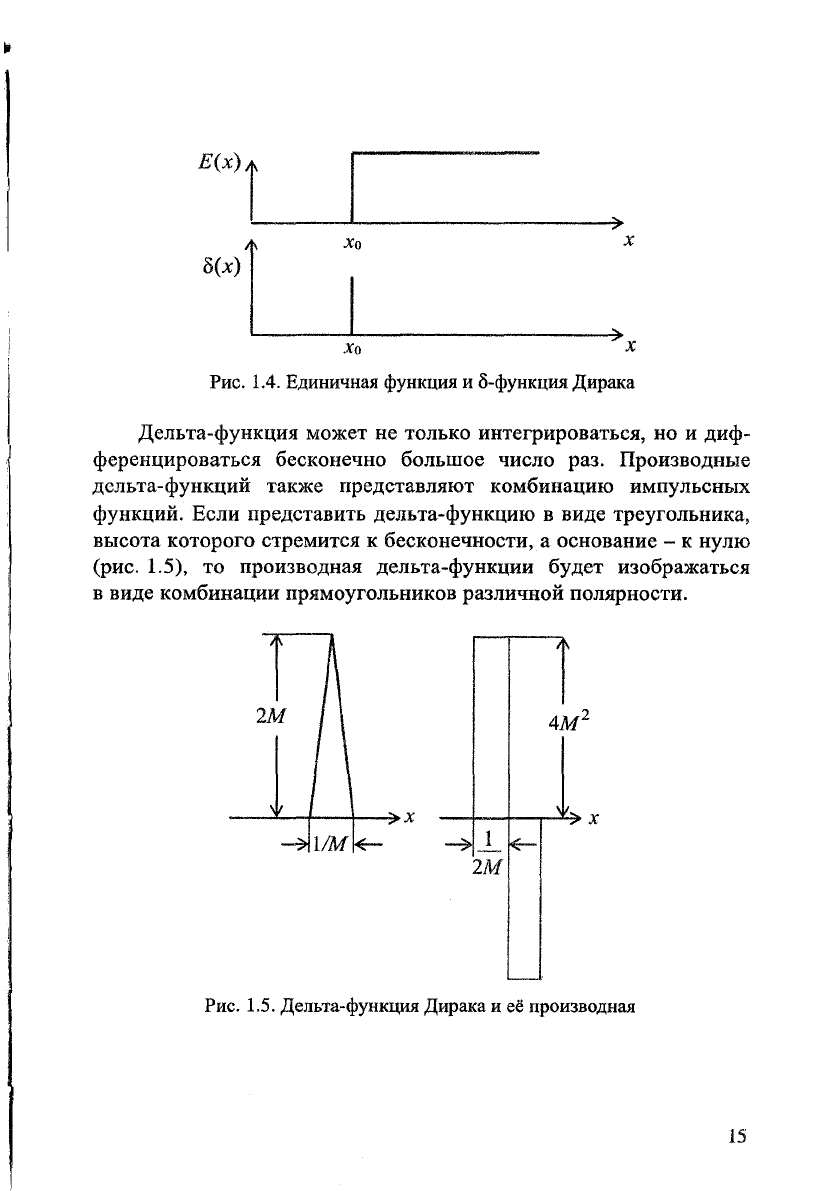
Е{х)

8(х)

Рис. 1.4. Единичная функция и 5-функция Дирака

Дельта-функция может не только интегрироваться, но и диф-

ференцироваться бесконечно большое число раз. Производные

дельта-функций также представляют комбинацию импульсных

функций. Если представить дельта-функцию в виде треугольника,

высота которого стремится к бесконечности, а основание - к нулю

(рис. 1.5), то производная дельта-функции будет изображаться

в виде комбинации прямоугольников различной полярности.

->J_L

2 М

Рис. 1.5. Дельта-функция Дирака и её производная

Производная дельта-функции имеет определённый физический

смысл. Если дельта-функция описывает плотность сосредоточенного

в точке тока, то её производная описывает плотность диполя - сис-

темы двух зарядов, удалённых друг от друга на бесконечно малое

расстояние [15].

В электротехнике дельта-функция может быть использована для

описания многих электрических величин. Известно, что объёмная плот-

ность электрических зарядов записывается в виде [16]

p = lim— при АУ —>0. (1.16)

AV"

При стремлении AV к нулю плотность р стремится к беско-

нечности. Поэтому приходится особо оговаривать, что AV имеет

конечные размеры, значительно меньшие, чем возможные расстоя-

ния между отдельными зарядами. Между тем объёмная плотность

электрических зарядов может быть математически строго описана

следующим выражением:

р = Д4-5(х-*

)8(у-з;

)б(г-г

), (1.17)

где х

,у

,г

- координаты точки расположения электрического

заряда.

Точно так же можно описать и поверхностную плотность заря-

дов - плотность электрического заряда, распределённого в поверхно-

стном слое, толщина которого стремится к нулю:

а = Пш— при AS —»0 . (1.18)

Д S

В терминах обобщенных функций поверхностная плотность за-

писывается как

о = д:

)б( v- у

). (1.19)

Вместе с тем необходимо отметить, что действие над самой дельта-

функцией не является корректной математической операцией, посколь-