Беляев Е.Ф., Шулаков Н.В., Дискретно-полевые модели электрических машин, учебное пособие

Подождите немного. Документ загружается.

ку её значение в данной точке равно бесконечности, т.е. не определено.

Для выполнения математических операций с дельта-функциями необ-

ходим переход от бесконечно больших величин к конечным. Этот пере-

ход осуществляется путём распределения дельта-функции на конечный

интервал пространственной координаты:

При математическом моделировании ЭМ приходится решать

сложные системы дифференциальных уравнений. Аналитические ре-

шения таких систем представляются возможными лишь в исключи-

тельных случаях, а для нелинейных уравнений практически невоз-

можны. Поэтому основными методами решения указанных уравнений

в настоящее время являются численные, предполагающие замену ана-

литических функций числовыми полями, над которыми производятся

необходимые математические операции. В связи с этим термин «ма-

тематическое моделирование» является адекватным термину «числен-

ное моделирование» или «численный эксперимент».

Таким образом, для реализации математической модели необхо-

дим переход от непрерывных аналитических функций к числовым

полям. Переход от непрерывных функций к последовательностям

дискретных значений величин обозначим как квантование функций.

С процессом квантования различных величин человек знаком

с древнейших времён. Различного рода измерения представляют не

что иное, как квантование этих величин. Именно операции с дис-

кретными величинами явились основой математики. С развитием

мысли в математике широкое распространение получил термин

«функция», и последовательности дискретных значений стали рас-

сматриваться в виде непрерывных последовательностей.

Новое рождение «кванта» появилось в работах М. Планка, когда

использование непрерывных функций не позволило решить задачу

(1.20)

1.2. КВАНТОВАНИЕ ФУНКЦИЙ

об излучении «чёрного» тела. С тех пор термин «квант» широко во-

шёл в обиход. Возникли новые понятия и термины: «квантовая меха-

ника» в механике, «квантовая биология» - генетика в биологии.

С этих позиций современные численные методы, широко используе-

мые для решения самых различных задач математики, с полным пра-

вом можно обозначить как «квантовая математика».

Для различного рода сигналов известны и широко используются

на практике следующие виды квантования функций [13, 18]:

- квантование по координате;

- квантование по уровню сигнала;

- квантование по частоте спектра.

Наиболее распространённым видом квантования, применяемым

в теоретических исследованиях и практике, является квантование по

временной или пространственной координате. При этом виде кван-

тования пространственная или временная координата делится на ряд

интервалов и в каждом из них производится измерение исследуемой

функции. Таким образом, непрерывная функция заменяется последо-

вательностью одиночных импульсов, величины которых равны зна-

чениям исследуемой функции на данном интервале пространствен-

ной или временной координаты (рис. 1.6). Указанный вид квантова-

ния лежит в основе всех конечно-разностных методов.

F(t)

Рис. 1.6. Квантование по координате

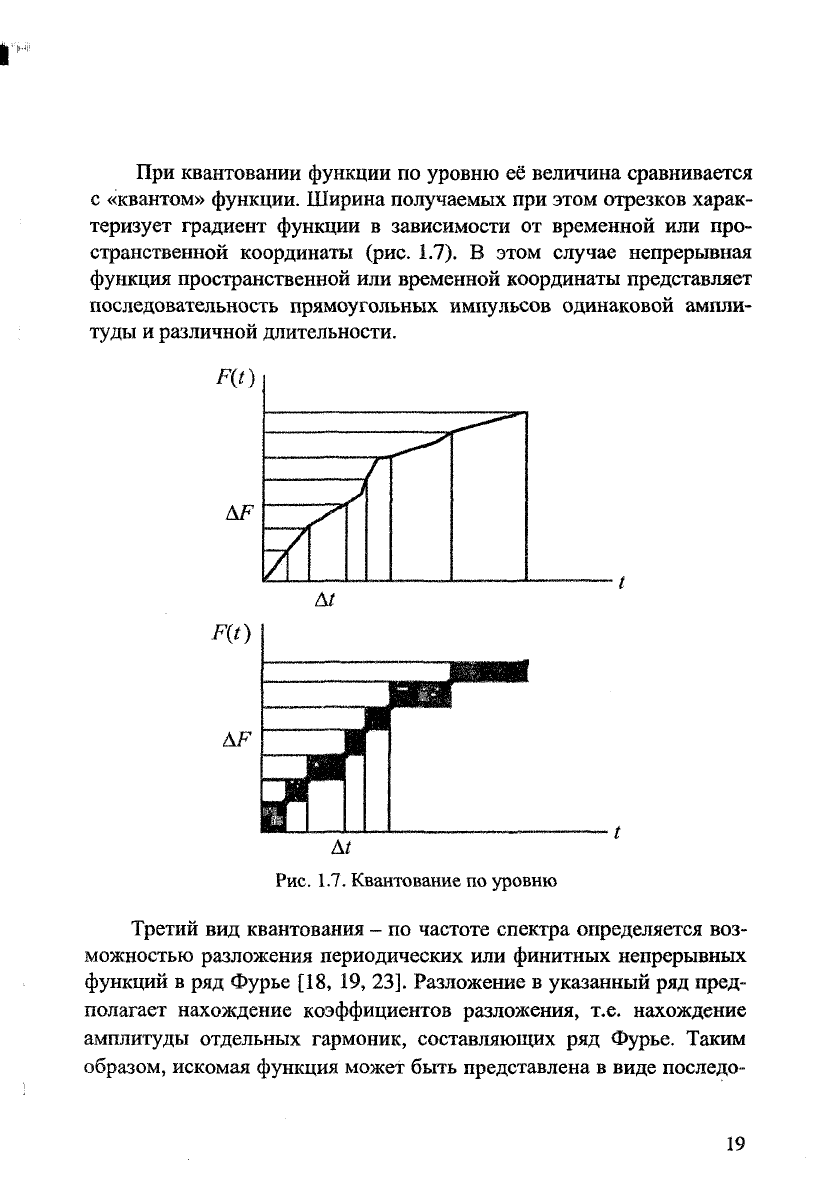
При квантовании функции по уровню её величина сравнивается

с «квантом» функции. Ширина получаемых при этом отрезков харак-

теризует градиент функции в зависимости от временной или про-

странственной координаты (рис. 1.7). В этом случае непрерывная

функция пространственной или временной координаты представляет

последовательность прямоугольных импульсов одинаковой ампли-

туды и различной длительности.

Рис. 1.7. Квантование по уровню

Третий вид квантования - по частоте спектра определяется воз-

можностью разложения периодических или финитных непрерывных

функций в ряд Фурье [18, 19, 23]. Разложение в указанный ряд пред-

полагает нахождение коэффициентов разложения, т.е. нахождение

амплитуды отдельных гармоник, составляющих ряд Фурье. Таким

образом, искомая функция может быть представлена в виде последо-

шт^змш шмшшшшшяшш

вательности гармоник заданных частот с определёнными амплиту-

дами. Для восстановления таких функций достаточно знание ампли-

туд гармоник в заданном интервале частот.

Для квантования математических функций в настоящее время наи-

более часто используется квантование по координате и частоте спектра.

Первый из этих способов лежит в основе конечно-разностных методов

решений уравнений, третий используется для решения уравнений в ча-

стных производных методом разделения переменных.

Что касается второго способа квантования-- квантования по

уровню, то этот способ для решения уравнений практически не при-

меняется, так как не разработан математический аппарат для систем

алгебраических уравнений, получаемых при аппроксимации диффе-

ренциальных уравнений. Хотя в ряде случаев, при квантовании

функций с малыми градиентами этот способ мог оказаться весьма

эффективным.

В основе математических способов квантования лежит возмож-

ность представления непрерывных функций в виде разложения по

системе базовых функций (СБФ) [18, 23, 27].

Для финитных непрерывных на интервале [а,Ь\ функций спра-

ведливо разложение

/(-*) = (1-21)

к-О

где С

- коэффициенты разложения; <p

- система базовых функций.

Для практических расчётов ряд усекают, ограничиваясь конеч-

ным количеством членов разложения.

Система базовых функций должна быть выбрана таким образом,

чтобы на данном интервале обеспечивался минимум среднеквадра-

тичной ошибки. Этому требованию отвечают системы ортогональ-

ных функций, которые чаще всего и используются для разложения

функций.

Для ортогональных систем базовых функций справедливо соот-

ношение

1ф*(*)Ф»(*)

л=5

ь,> о-

)

ще - символ Кронекера,

Г1при* = «,

(12з)

[О при к

т.

Ортогональная система считается нормированной, если её норма

равна единице:

j(p

dx =

l. (1.24)

Такие функции называются ортонормальными. Коэффициенты

разложения ортонормальных функций определяются по обобщённой

формуле Фурье:

С* = -^-1/(4h<b- (1-25)

Ь-а

Существует бесчисленное множество ортонормальных базовых

функций, однако на практике используются лишь некоторые из них.

1. Система единичных базовых функций. Любая точка непре-

рывной финитной функции может быть выражена в виде интеграла

от дельта-функции:

f(a)=]f(x)5(x-a)dx. (1.26)

Если заставить любую точку непрерывно изменять свои координа-

ты, то указанный интеграл будет определять семейство точек,

принадлежащих непрерывной кривой. Другими словами, любую

непрерывную на интервале функцию можно представить в виде

разложения:

f(x) =

(1.27)

Ввиду неопределённости дельта-функции в каждой рассматри-

ваемой точке, от бесконечно малых интервалов в разложении пере-

ходят к конечным величинам Ах. В этом случае вместо интеграла

будем иметь

/(х) = ]Г/(Мх)5(х-£Дх)Лх, (1.28)

*=о

где N - число интервалов разбиения пространственной координаты,

N = (1.29)

Ах

Дельта-функция представляется в виде прямоугольного импуль-

са с единичной площадью, шириной Ахи высотой 1/Дх. Подставляя

выражение дельта-функции в формулу (1.29), получим

= • О.30)

Если обозначить С

= f (кАх), (рДх) = , то получим форму-

лу (1.21).

Полученное выражение говорит о том, что финитную на интерва-

ле [а,Ь\ функцию можно представить в виде разложения по системе

единичных базовых функций, представляющих единичные импульсы

Ах, смещённые друг от друга на ширину импульса и заполняющие

рассматриваемый интервал. Такая система является ортонормальной

и полной для ступенчатых функций с шириной ступени Ах. При

стремлении интервала Ах к нулю система базовых функций становит-

ся полной для непрерывных функций, однако для реализации такого

разложения требуется бесконечно большое число членов разложения.

Достоинством единичных базовых функций является то обстоятельст-

во, что значение коэффициента разложения С

равно значению разла-

гаемой функции в данной точке, т.е. для нахождения их значений не

требуется затрат математических операций. Разложение функций по

системе единичных базовых функций соответствует их квантованию

по пространственной координате.

2. Система тригонометрических базовых функций. Является

полной и ортогональной на интервале [0,2л] или [-я,

тс].

Для непре-

рывных периодических и финитных функций на интервале длиной 21

с тем же периодом возможно разложение

кюс . кжх

/М

]Г а

cos

—— +

Z?*sin —-

i v

I l

(1.31)

причём коэффициенты разложения определяются в виде обобщённой

формулы Фурье:

ak=~f/(x)cos~dx; (1.32)

1 kfCC

= ~\f(x)sm—dx. (1.33)

При численном решении дифференциальных уравнений часто

используется система ортонормальных дискретных тригонометриче-

ских базовых функций, определяемая на интервале разложения

[О,

N ] выражением

(1-34)

*=0

коэффициенты разложения которого определяются следующим

образом:

2 лм 2 laii

=—V/(i)cos ; b

~—V/(i)sin—. (1.35)

* Wtr N

Nt: N

При решении дифференциальных уравнений с комплексными ко-

эффициентами используется разложение с дискретными комплексны-

ми экспоненциальными базовыми функциями:

ЛГ-1 .2Ш

/(«•) = £<:, е'" , (1-36)

к=О

где коэффициенты разложения рассчитываются по формуле

* • (1-37)

А (=0

Особенностью разложений по тригонометрическим и экспонен-

циальным базовым функциям является то, что расчёт коэффициентов

разложений и восстановления функций требуют определённых за-

трат математических операций.

Кроме рассмотренных базовых функций при исследовании раз-

личных процессов, описываемых уравнениями в частных производных

широко используются полиномы Чебышева, Лежандра, а также специ-

альные функции Уолша, Радемахера, Наара и некоторые другие.

1.3. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ

При математическом описании электромагнитных процессов

электрических машин используются дифференциальные уравнения в

частных производных, которые в общем виде для двух пространст-

венных координат записываются следующим образом:

Эх

Э и

i—

Эх

+ -

Эх

Э и

>— -I—„

ду J ду

д и

Эх

д ( д и

—I

—

Эу

^ ду

+ F{x,y,u)

0. (1.38)

Коэффициенты этого уравнения - это кусочно-непрерывные

функции пространственных координат, не обращающиеся в нуль

одновременно во всей исследуемой области.

Путём замены переменных указанные уравнения в зависимости

от характера и знака коэффициентов могут быть приведены к одному

из следующих видов [15,20]:

1. Уравнение эллиптического типа

£!и>

+ф1 =

о. (1.39)

Эр

да

По аналогии с уравнением эллипса

4+4=

а-40)

J L

a b

дифференциальное уравнение (1.39) принято называть уравнением

эллиптического типа. Это уравнение описывает пространственное

распределение исследуемых величин в стационарных режимах.

Частными случаями этого уравнения являются уравнения Пуассона

и Лапласа:

2. Уравнение гиперболического типа

Ui d

Эр

до

+ ф,

0. (1.42)

По аналогии с уравнением гиперболы

= 0 (1-43)

-Г Л

a b

это уравнение носит название гиперболического. Примером уравне-

ния гиперболического типа является уравнение, описывающее коле-

бательные процессы при распространении электромагнитного поля

в пространстве:

dhi д ( ди) д ( ди

" Кггг

^ dt

дх \

Эх J by

ду

-q-u

F(x,y,t). (1.44)

3. Уравнение параболического типа

ди Эм

—j-Л—+ ф, = 0.

Эр Эа

Это уравнение уподоблено уравнению параболы, которое в де-

картовой системе координат записывается в виде

у =2 рх

с.

(1.46)

Примером такого уравнения является уравнение теплопроводно-

сти, описывающее нестационарный процесс пространственного рас-

пространения тепла в среде

f s \

ди

dt Эх

д( ди\Э_

'Эх) ду

К 2

ди

Ту

•qu + F(x,y,t). (1.47)

В общем случае дифференциальные уравнения параболического

типа описывают нестационарные процессы распространения субстан-

ции в средах, обладающих определёнными характеристиками (распро-

странение вещества в окружающем пространстве - процесс диффузии,

проникновение магнитного поля в электропроводную среду и т.п.).

1.4. КРАЕВЫЕ ЗАДАЧИ И ГРАНИЧНЫЕ УСЛОВИЯ

Решение дифференциальных уравнений в частных производных,

так же как и обычных дифференциальных уравнений, неоднозначно

и представляет собой семейство определённых функций. Для того

чтобы иметь однозначное решение, необходимо использовать гра-

ничные условия, т.е. условия на границах исследуемой области.

Обычно эти условия являются следствиями определённых физиче-

ских законов, соответствующих рассматриваемой задаче. Совокуп-

ность дифференциального уравнения и граничных условий опреде-

ляет краевую задачу. Различают следующие виды граничных усло-

вий [15, 20, 24]: