Беляев Е.Ф., Шулаков Н.В., Дискретно-полевые модели электрических машин, учебное пособие

Подождите немного. Документ загружается.

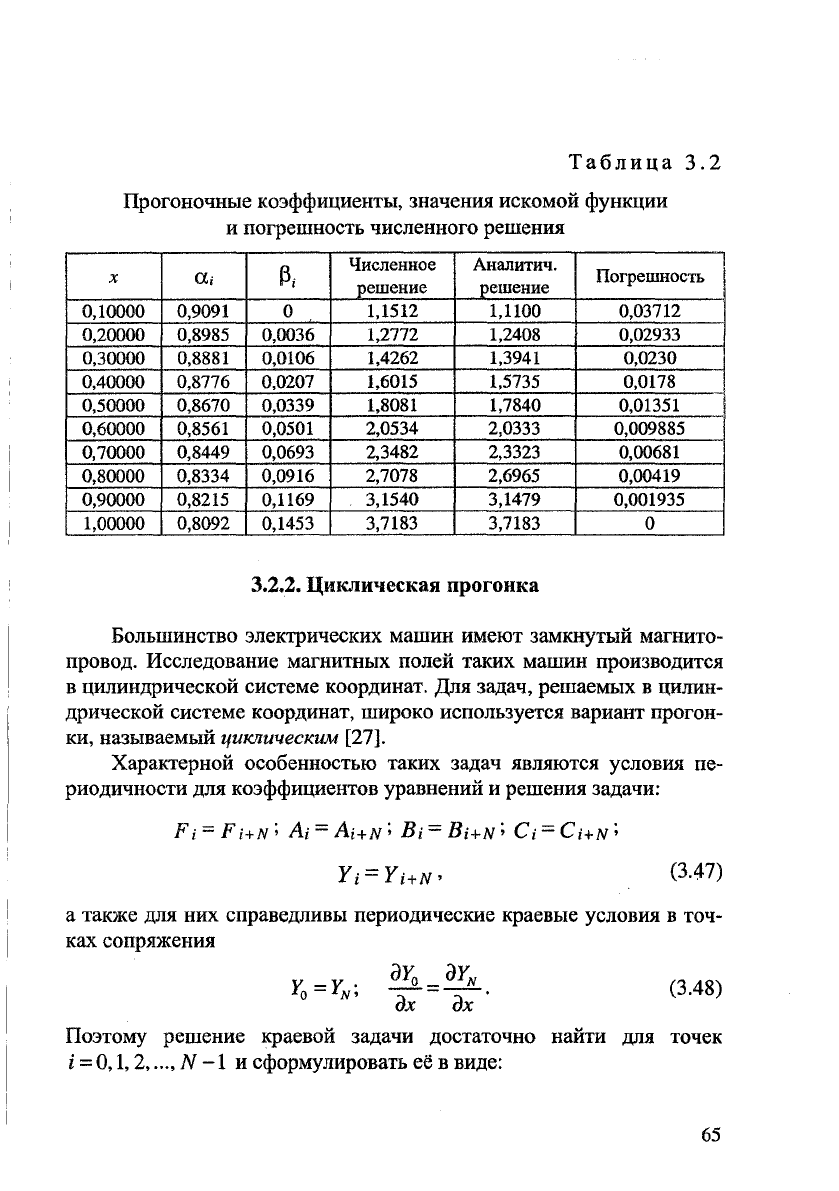
Таблица 3.2

Прогоночные коэффициенты, значения искомой функции

и погрешность численного решения

ОС;

Р,

Численное

решение

Аналитич.

решение

Погрешность

0,10000 0,9091

1,1512

1,1100

0,03712

0,20000 0,8985 0,0036

1,2772

1,2408 0,02933

0,30000 0,8881

0,0106

1,4262

1,3941 0,0230

0,40000 0,8776

0,0207 1,6015

1,5735

0,0178

0,50000

0,8670 0,0339 1,8081

1,7840 0,01351

0,60000 0,8561

0,0501

2,0534

2,0333 0,009885

0,70000 0,8449

0,0693 2,3482

2,3323

0,00681

0,80000 0,8334 0,0916 2,7078 2,6965 0,00419

0,90000 0,8215 0,1169 3,1540 3,1479 0,001935

1,00000

0,8092

0,1453 3,7183 3,7183 0

3.2.2. Циклическая прогонка

Большинство электрических машин имеют замкнутый магнито-

провод. Исследование магнитных полей таких машин производится

в цилиндрической системе координат. Для задач, решаемых в цилин-

дрической системе координат, широко используется вариант прогон-

ки, называемый циклическим [27].

Характерной особенностью таких задач являются условия пе-

риодичности для коэффициентов уравнений и решения задачи:

Fi - Fi+N' Ai = Ai+м

Bi = Bi+N' Ci = Ci+N

;

Yi = Y

i+N

, (3-47)

а также для них справедливы периодические краевые условия в точ-

ках сопряжения

Го-Ъ; = (3.48)

ох ох

Поэтому решение краевой задачи достаточно найти для точек

= 0,1,2,..., N -1 и сформулировать её в виде:

'aoYN-I-CoYO

+ BOYI = -FO> * =

- AiYi-x~CiYi

+ BiYi+i =

~Fi, l<i<N-l- (3.49)

= UO-

Будем искать решение как сумму составляющих

Ui + Y

Vi, 0<i<N, (3.50)

где U

- решение неоднородной задачи с однородными краевыми ус-

ловиями:

A.f/

-C

JЩ

=-F

l<i<N-l; (3.51)

иo =

-0;

- решение однородной задачи с неоднородными краевыми ус-

ловиями:

Л^-1 ~ СХ

+ B,V

=0,

1 <

N -1; (3.52)

Vo=i;

= i-

В полном соответствии систем (3.51) и (3.52) краевой задаче

(3.49) можно убедиться, умножив (3.52) на Y

сложив с (3.51).

Каждая из краевых задач (3.51) и (3.52) решается методом про-

гонки, описанным выше:

= OLinU,ч1 +

Ры; Vi

Y(+i, г

= iV-1,

ЛГ

- 2,1;

_ Bt . p _ F,

Afi, . _ Ailj

tti+l

—

5 — > Ij+i ~ »

Ct-mAi Ct-mAi Ci-щА,

i = l, 2, ...,N -I, N ;

0<i<N,

= 1,2,...JV-1.

Для реализации циклической прогонки необходимо затратить

14ЛГ—8 математических операций на один интервал разбиения про-

странственной координаты, т.е. этот метод также является эконо-

мичным. При соблюдении условий устойчивости прогонки накопле-

ния ошибки не происходит, счёт является устойчивым.

Пример 3.2. Решение периодической задачи методом цикличе-

ской прогонки. В области [0,2ж] решим краевую задачу

3 ¥

-0,446Г = -/(х)

Эх

с периодическими краевыми условиями

Y(0)

У (2л)

= О,

Эх

Ч Уо

ил j

2п

ЭУЛ

Эх

)

Правая часть дифференциального уравнения является функцией про-

странственной координаты и для 24 интервалов имеет следующие

значения:

..f

0; /

.../

= 0,137; /

.../

= 0;

.../

= -0,137; /

.../

= 0.

Исследуемая область разбивается на N - 24 пространственных

интервалов величиной

= 2iz/N = 0,26lS.

Дифференциальный оператор аппроксимируется конечно-раз-

ностным выражением со вторым порядком точности и подставляется

в уравнение

YM-2Yi+Yi-i

-0,446Y,=-f

Преобразуя это выражение, получаем систему трёхчленных ал-

гебраических уравнений для всех интервалов разбиения пространст-

венной координаты:

AiYi-1 - CiYi + BiYi+i

—

~Ff i

1,2, ...,N-l,N ,

где Д =

В, =1; F. = f

\; C,= 2 + 0,446ft

; Y

Ay.

= —. I = 2,...,N, UN-I = $

', VN-I = A

+ y

С,-Д.а,.

U, = ам£/м + Р

; V;. =a

j+1

V;.

i+1

, i = N-2,N-3,..., 2,1;

Y^U^YNV,, i = l, 2,..., iV-1;

1 Yw+i ^w+i^i

•

У = У •

N+1 >

l Эх J, 2h

По полученным данным построены графические зависимости

А(х) = Y(x) и В(х) = У'(х), которые описывают распределение век-

торного потенциала и магнитной индукции по длине расточки стато-

ра (рис. 3.2).

А, Вб/м

В, Тл

Рис. 3.2. Пространственное распределение векторного

потенциала (а) и магнитной индукции (б)

Программа решения краевой задачи:

n=24; dx=2.*pi/n;

а(1:п+1)=1.;

Ь(1:

п+1)=1.;с(1: п+1)=а(1: n+l)+b(l: n+l)+0.446*dx

2;f(l:n+l)=0;

rl=0.137*dx

2; f(3:10)=rl

;

f(15:22)=-rl; ss(l:n)=0.;

alf(2)=0.; bet(2)=0.; gam(2)=l.;

disp(a); disp(b); disp(c); disp(f); disp(alf); disp(bet); disp(gam);

for j=l:n

nn(j)=j;

end

forj=2:n+l

r=c(j)-a(j)*alfG); alf(j+l)=b(j)/r; bet(j+l)=(f(j)+a(j)*bet(j))/r;

gam(j+l)=a(j)*gam(j)/r;

end

u(n)=bet(n+l); v(n)=alf(n+1 )+gam(n+1);

for j=n-l:-l:2

u(j)=alf(j+1 )*u(j+1 )+bet(j+1); v(j)=alf(j+l)*v(j+l)+gam(j+l);

end

r2=bet(n+2)+alf(n+2)*u(2); r3=l.-alf(n+2)*v(2)-gam(n+2); y(n+l)=r2/r3;

y(l)=y(n+l);

for

j=2:n

y(j)=u(j)+y

(n+1) * v(j);

end

bl( 1

)=(y(2)-y(n))/

(2. *dx);

bl(n)=(y(

)-y(n-1 ))/(2.*dx);

for j=2:n-l

bl(j)=(y0+l)-y(j-l))/(2.*dx);

end

nl(nn)=nn; n2(nn)=ss; n3(nn)=bl(l:

n);

n4(nn)=y(l:

n);

disp(y); disp(bl);

plot(nl,n2,nl,n3,ni

,n4)

Результаты решения задачи приведены

табл.

3.3, 3.4.

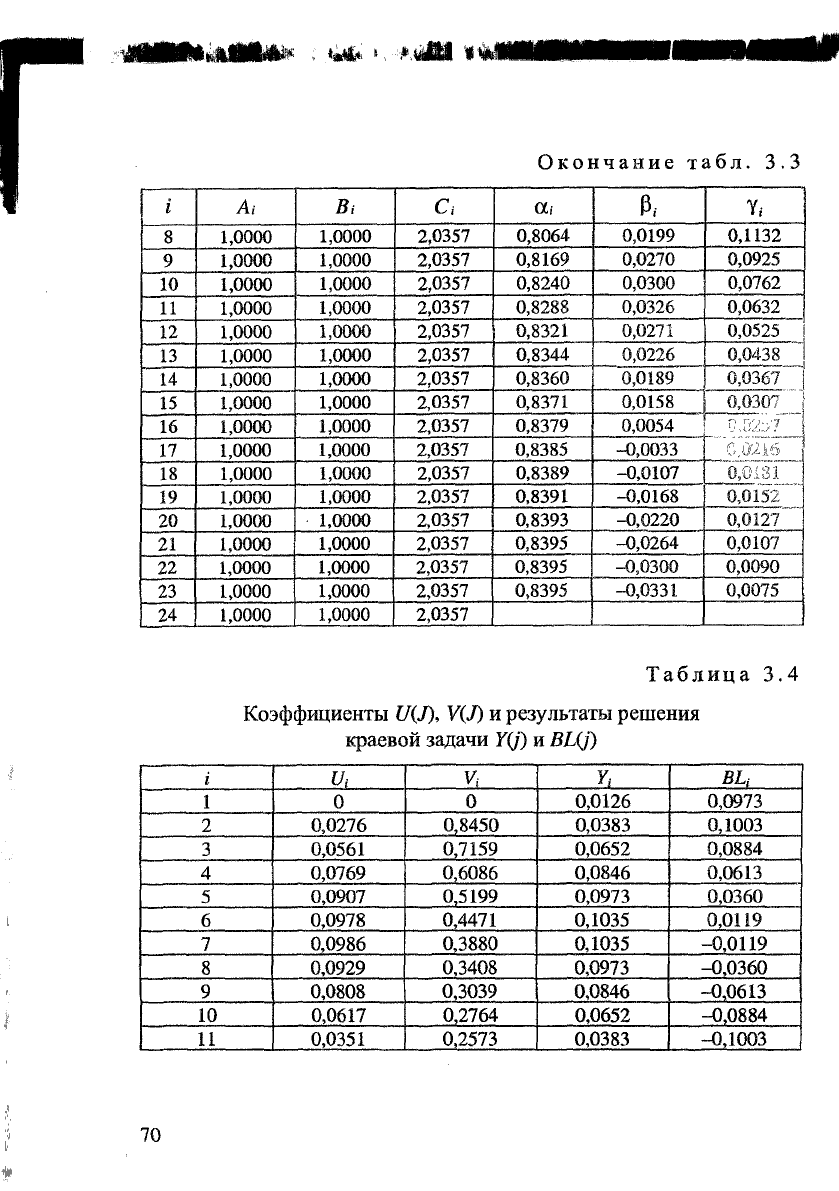
Таблица

3.3

Коэффициенты системы алгебраических уравнений

прогоночные коэффициенты

А,- Bi

с, а,

У,-

1,0000 1,0000 2,0357 0.0000 0,0000 0,0000

1,0000 1,0000 2,0357 0.0000 0,0000 1,0000

1,0000

1,0000 2,0357 0,4925 0,0000

0,4925

1,0000

1,0000 2,0357

0,6502

0,0061 0,3202

1,0000 1,0000 2,0357

0,7244

0,0112 0,2319

1,0000 1,0000

2,0357

0,7656 0,0158

0,1776

1,0000

1,0000 2,0357 0,7905 0,0199 0,1404

•шяшшлт

<•*» v£ti

Окончание табл.

3.3

Ai Bi Ci

а.

Р,

1,0000

1,0000 2,0357

0,8064

0,0199 0,1132

1,0000

1,0000 2,0357

0,8169

0,0270 0,0925

1,0000

1,0000 2,0357

0,8240 0,0300

0,0762

1,0000

1,0000 2,0357

0,8288 0,0326 0,0632

1,0000

1,0000 2,0357

0,8321 0,0271

0,0525

1,0000

1,0000 2,0357

0,8344

0,0226

0,0438

1,0000

2,0357

0,8360 0,0189 0,0367

1,0000

1,0000 2,0357 0,8371

0,0158 0,0307

1,0000

1,0000 2,0357

0,8379

0,0054

1,0000 1,0000

2,0357 0,8385

-0,0033

С.ДЦ6

1,0000

1,0000 2,0357

0,8389 -0,0107

0,0181

1,0000

2,0357 0,8391

-0,0168 0,0152

1,0000

1,0000 2,0357

0,8393 -0,0220

0,0127

1,0000

1,0000 2,0357 0,8395

-0,0264

ГадТот

1,0000

1,0000 2,0357

0,8395 -0,0300 0,0090

1,0000

2,0357 0,8395 -0,0331

0,0075

1,0000

1,0000 2,0357

Таблица

3.4

Коэффициенты U(F),

V(J) и

результаты решения

краевой задачи

Y(j) и ВЩ)

и,

BL,

1 0 0

0,0126 0,0973

0,0276 0,8450 0,0383

0,1003

0,0561 0,7159

0,0652

0,0884

0,0769 0,6086

0,0846 0,0613

0,0907

0,5199 0,0973

0,0360

0,0978

0,4471 0,1035 0,0119

0,0986

0,3880

0,1035

-0,0119

0,0929

0,3408

0,0973

-0,0360

0,0808 0,3039 0,0846 -0,0613

0,0617

0,2764

0,0652

-0,0884

0,0351

0,2573 0,0383 -0,1003

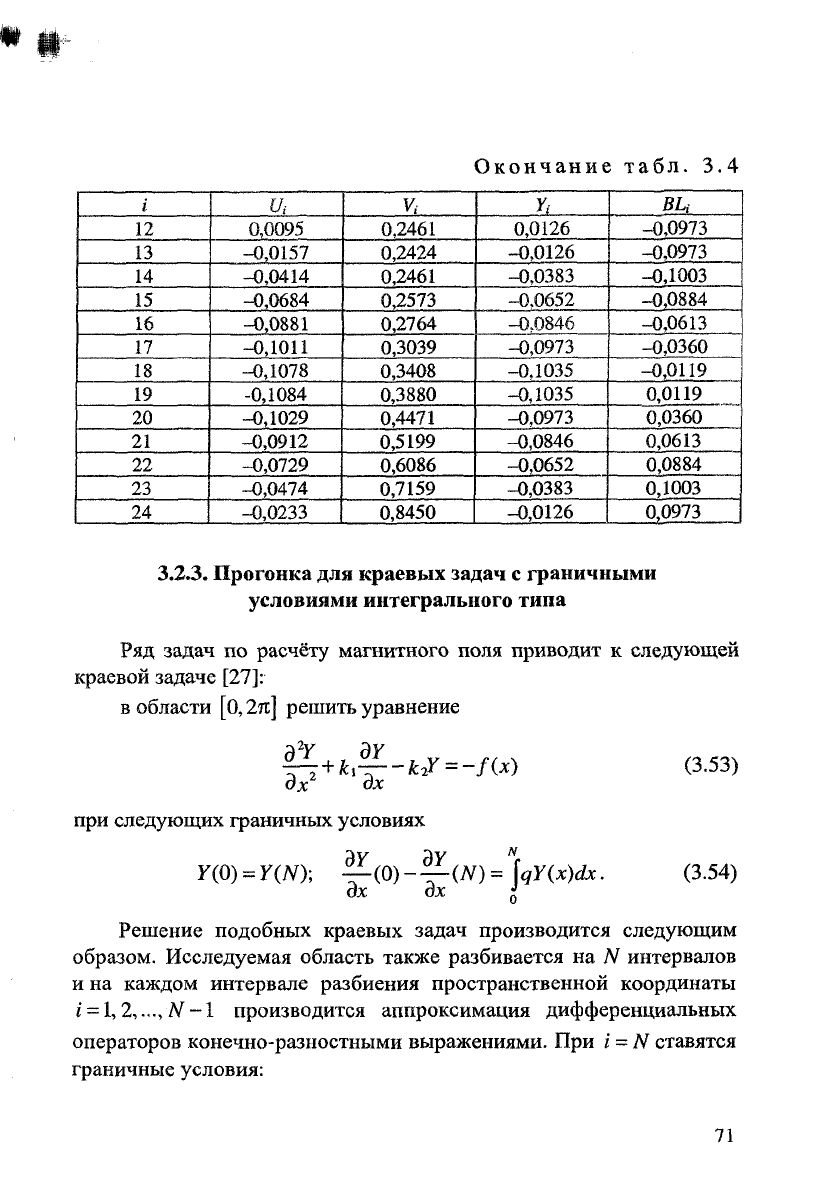
Окончание табл. 3.4

у,

ви

12 0,0095 0,2461

0,0126 -0,0973

-0,0157

0,2424

-0,0126

-0,0973

14 -0,0414 0,2461

-0,0383 -0,1003

-0,0684

0,2573

-0.0652 -0,0884

-0,0881

0,2764

-0.0846

-0,0613

-0,1011

0,3039

-0,0973 -0,0360

18 -0,1078 0,3408

-0,1035 -0,0119

19 -0,1084 0,3880

-0,1035

0,0119

20 -0,1029

0,4471

-0,0973 0,0360

21 -0,0912 0,5199

-0,0846 0,0613

22 -0,0729

0,6086

-0,0652 0,0884

23 -0,0474

0,7159

-0,0383

0,1003

24 -0,0233

0,8450

-0,0126 0,0973

3.2.3. Прогонка для краевых задач с граничными

условиями интегрального типа

Ряд задач по расчёту магнитного поля приводит к следующей

краевой задаче [27]:

в области [0,2л] решить уравнение

+ k^-k

Y = -f(x) (3.53)

дх

при следующих граничных условиях

У(0) = Г(Л0; ^(0)-|^(Л0 = (3.54)

дх ох •

Решение подобных краевых задач производится следующим

образом. Исследуемая область также разбивается на N интервалов

и на каждом интервале разбиения пространственной координаты

1,2,..., N -I производится аппроксимация дифференциальных

операторов конечно-разностными выражениями. При i = N ставятся

граничные условия:

v -х/ . FiFO Yn~Yn-I

Fo-F*; — ; = 2;4i

(3.55)

Fi Yо F/v F/v-i _

i=0

или

Fi-Fp

FA? ~Улг-1

v T7 /1

= 2^<liYi. (3.56)

hx hi i~0

Согласно краевым условиям

YO =

YN уравнение (3.56) может

быть преобразовано:

№ +

(3.57)

hi ы

или

12 1

~~ZYi-(~j

+ 77 = X • (3-58)

я* h

hx i=i

Таким образом, получается следующая система:

hx hx ;=i

AiFo

CiFi + B\YI = ~F\

'=1;

AiYi-i ~ CiYt

BiYi = -F,, i = 2,3,...,

- 3;

AJV-2Fn-3

CN-2YN-2 + BN-2YN-I = ~FN-

i = N - 2;

AN-IYN-2 - CN-IYN-I + BN-\YN = ~FN- 1, i = N-1;

= Fw

В общем виде такая система записывается в следующем виде:

AfFi-i ~ C,F, + J3iF;+i = ~FI> i=l, 2,...,

-1; (3.59)

w-i

ANYN-I ~ CNYN +

BjvFI

= ~ X#

Fi> i =

(3.60)

1=1

и её решение ищется в виде суммы двух составляющих:

Yi = Ui + YNVi, (3-61)

здесь Ui - решение неоднородного уравнения с однородными гра-

ничными условиями

AiUj-i~CiUi + BiUi+i

~Fi, i = 1,2,-, N-l, (3.62)

= 0; U

= Q,

Vi - решение однородного уравнения с неоднородными граничными

условиями

ЛАЛ-1

~ С,У, + ВУ

= 0,

2, ...,N -1, (3.63)

= l; V

= 1-

Каждая из этих систем решается методом прогонки. В результате

решения задачи (3.62) получаем значения Ui, а решения задачи (3.63) -

значения

для i = l, 2,..., N-l.

Запишем решение уравнения (3.53) для i

YN-^UN-1 + YNVN-I; (3.64)

YI = UI + YNVI- (3-65)

Подставляя эти выражения в (3.54), будем иметь

(UN-

+ FjvVtf-i) ~ CNYN + B

{Ux + YNVI) =

n=T (3.66)

= -F

-L<li{Ui

Vi)-

i-1

Решая уравнение (3.66) относительно Y

, получим

N-l

ANUN-I + BNUI + FN + YiW*

YN= £ • (3-67)

CH-AnVH-i-BsVi-^qy,

i=i

Определение других значений У, производится по выражению

(3.61).

Поскольку каждая из краевых задач (3.62), (3.63) решается мето-

дом прогонки, выполняются условия устойчивости счёта. Знаменатель

выражения (3.67) отличен от нуля. Следовательно, решение краевой

задачи существует, устойчиво и исключает накопление ошибок.

3.3. РЕШЕНИЕ НЕСТАЦИОНАРНЫХ КРАЕВЫХ ЗАДАЧ

Нестационарные краевые задачи описываются уравнениями

параболического типа, совместно с краевыми условиями, а также

начальными условиями, задающими распределение исследуемой

функции в начальный момент времени. Рассмотрим простейшую

одномерную краевую задачу:

^- = K(x,t)^ + f(x,t) (3.68)

dt д

с краевыми условиями первого рода

u(0,t) =

a-,

U(L,t) = b

и начальными условиями

£/(X,0) = 8(jc).

Для решения уравнения исследуемая область разбивается на N

пространственных интервалов, временные и пространственные диф-

ференциальные операторы аппроксимируются конечно-разностными

выражениями, в результате чего дифференциальное уравнение заме-

няется системой алгебраических уравнений, решаемых совместно

с граничными и начальными условиями известными методами. По-

мимо дифференциальных операторов в ряде случаев приходится ап-

проксимировать правую часть уравнения и дополнительные условия

краевой задачи. Точность получаемого решения зависит от способов

аппроксимации и величины интервалов разбиения пространственных

и временной координат. Путем изменения этих величин получается