Беляев Е.Ф., Шулаков Н.В., Дискретно-полевые модели электрических машин, учебное пособие

Подождите немного. Документ загружается.

for i=30:15:210

a(i,i-15)=kl; a(i,i-l)=kl; a(i,i)=-k2; a(i,i+15)=kl;

end

for i=2:14

a(i,i-l)=kl; a(i,i)=-k2; a(i,i+l)=kl; a(i,i+15)=kl;

end

for i=212:224

a(i,i-15)=kl; a(i,i-l)=kl; a(i,i)=-k2; a(i,i+l)=kl;

a(l,l)=-k2; a(l,2)=kl; a(l,16)=kl; a(15,15)=-k2; a(15,14)=kl; a(15,30)=kl;

a(211,212)=kl; a(211,211)=-k2; a(211,196)=kl; a(225,225)=-k2; a(225,224)=kl;

a(225,210)=kl;

while ncnk

fk(l:225)=-x0(l:225)+f(l:225); x=fk/a; x0(l:225)=x(l:225); t=t0+dt*n; n=n+l;

y(n)=x(113);

z(n)=n; disp(n); disp(x(113));

end

disp(x); plot(z,y)

Установившиеся значения искомой величины, полученные при

решении краевой задачи с использованием явной и неявной схем,

полностью совпадают. Неявная схема является безусловно устойчи-

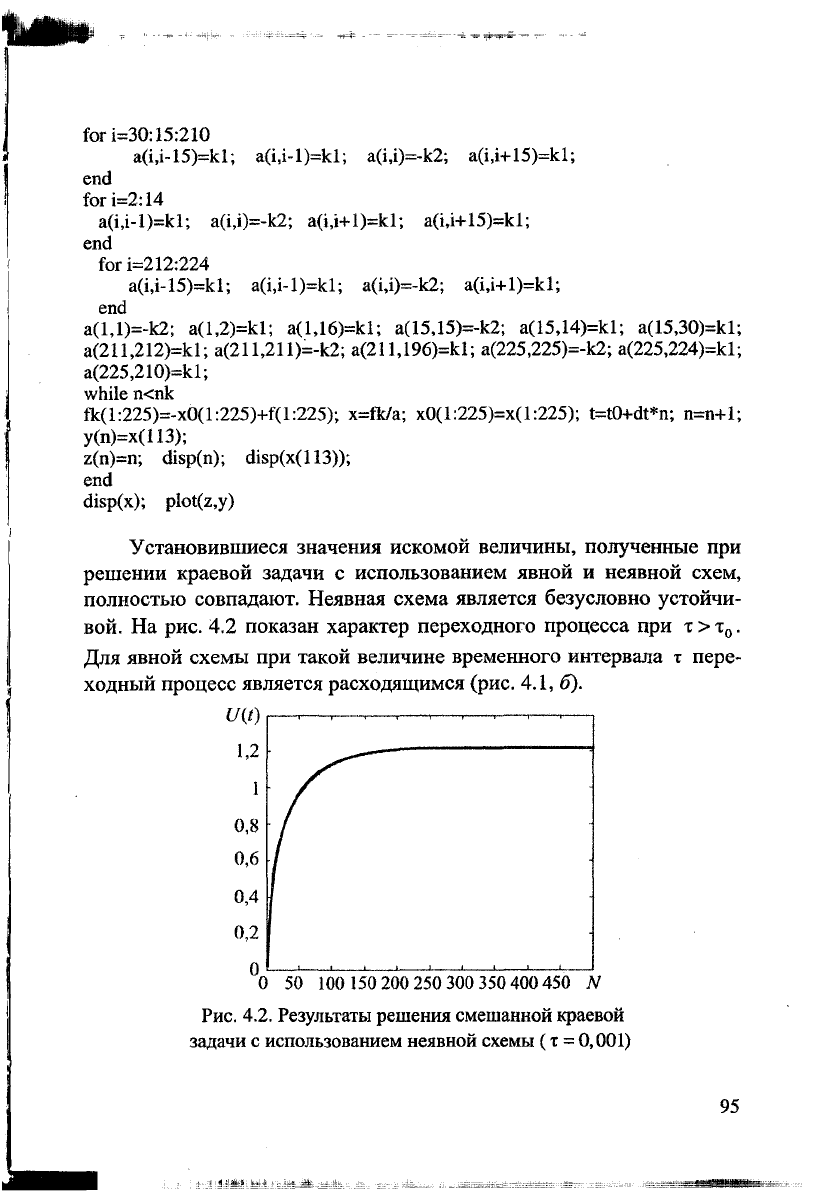
вой. На рис. 4.2 показан характер переходного процесса при х > т

Для явной схемы при такой величине временного интервала т пере-

ходный процесс является расходящимся (рис. 4.1, б).

U (t) — — —•—•— —

end

0,4

0,2

0,8

0,6

0 50 100 150 200 250 300 350 400 450 N

Рис. 4.2. Результаты решения смешанной краевой

задачи с использованием неявной схемы (т = 0,001)

Приведённые рассуждения показывают, что как явная, так и не-

явная схемы не экономичные: число математических операций на

одно неизвестное не является постоянным. Однако для решения мно-

гомерных уравнений параболического типа существуют экономич-

ные схемы с затратой постоянного числа операций на одну точку ис-

следуемой области, к которым относится рассматриваемый ниже ме-

тод переменных направлений.

4.2. МЕТОД ПЕРЕМЕННЫХ НАПРАВЛЕНИЙ

Одним из наиболее часто используемых на практике методов ре-

шения нестационарных краевых задач является метод переменных на-

правлений, называемый часто продольно-поперечной схемой [23,24,25].

Решение задачи с использованием этого метода производится

следующим образом. Временной интервал разбивается на два полу-

целых слоя, и на каждом из них решается краевая задача с использо-

ванием неявной схемы по одной координате и явной - по другой.

Полученное при этом решение принимается в качестве начального

для второго полуцелого временного слоя, на котором меняются на-

правления явной и неявной схем. Дифференциальное уравнение при

этом заменяется двумя конечно-разностными уравнениями:

j j/1+0,5 _

0,5

_,_f/rtO,5

(t/;r -v\.,)=

i+1J

U'w-WIj+UIm , f'u

f'u.

. Tjt+0,5 _ ryrji+0,5 rr(+0,5

^ИУ-^ГН,

1MJ

ii '-

U'jj+i

~ 2U'ij + yi) /Ь + ЯГ

+кг

(4.7)

(4.8)

Первое из этих уравнений содержит три неизвестные

UMJ, U'ij'\

U'i-LJ,

значения величин второй группы U',

J+

b U'ij,

U'u-i известны из решения задачи на предыдущем временном

слое или из начальных условий при начале счёта. Поэтому первое

уравнение может быть решено методом прогонки вдоль направле-

ния координаты i для всех значений j = 1,2,...,N

-l. Точно так

же для второго уравнения (4.8) неизвестными величинами будут

и\%, и и, и'См, а значения Umj, U'u'

> Utij определены на

предыдущем полуслое. Второе уравнение решается методом про-

гонки вдоль направления координаты j для всех значений

i = l,2,...,N

-1 (рис. 4.3).

Рис. 4.3. К решению краевой задачи методом

переменных направлений

Оценим погрешность метода переменных направлений. Обозна-

чив дискретные операторы Лапласа как Д, и Д

, суммируя уравне-

ния (4.7) и (4.8), получим

и'

+ °'

5А

2 (

+ u

lj)

f'u*

•

(4-9)

Определим U\*f'

, вычитая из уравнения (4.8) уравнение (4.7):

=0,5 +u;,

)~~A

(uu'

;

'-uU)

•

(4.10)

Подставляя полученное выражение в (4.9), будем иметь

,+1

— II'

= 0,5л, (ufi+u'

)+о,5A

(

;;; +

) -

-A

t+0,5

ИЛИ

Utf-Ub

= 0,5 (A, + Д

) и

'£}

+ 0,5 (A, + A

)

1+f

, (4-12)

В этом уравнении все члены за исключением последнего обра-

зуют симметричную неявную схему, рассмотренную ранее, обла-

дающую вторым порядком точности, как по временной координате,

так и по пространственным. Дискретный оператор Лапласа обеспе-

чивает второй порядок точности по пространственной координате.

Следовательно, последний член этого выражения обладает четвёр-

тым порядком по пространственным координатам. Для определения

погрешности этого члена по временной координате разложим функ-

ции U'ijii U'ij в ряд Тейлора в окрестности точки и'С°'

\(+0,5

х(ъи_

l{dt ),, ' 2U

+И

' -п'

(

21 Эt Д

\<+0,5

и'

и', j

•

<^.

v+0

v Л;

Тогда

(диЛ

, =

т —-

(+0,5

и последний член уравнения (4.12) может быть записан в виде

*(ди Y

(4.13)

(4.14)

(4.15)

(4.16)

т.е. имеет второй порядок точности по временной координате.

При решении одномерных краевых задач методом прогонки

приходится использовать граничные условия (4.2). Если значения

функции на границах от времени не зависят, то проблем с их задани-

ем для любого момента времени не возникает. Точно так же значения

функций на границах однозначно определены в моменты времени,

соответствующие целочисленным слоям t, t

+1,

t + 2,... В этом случае

величина ]i(x,t) задаётся для соответствующего момента времени.

Если же рассматриваются промежуточные временные слои

Г+ 0,5; г+ 1,5; t + 2,5..., то граничные значения функций так-

же должны соответствовать этим моментам времени. Принимая гра-

ничные значения, соответствующие целочисленным моментам вре-

мени, мы допускаем погрешность, так как на промежуточных вре-

менных слоях значения функций должны соответствовать

выражению (4.10). Поэтому, чтобы обеспечить второй порядок точ-

ности по временной координате, граничные условия на промежу-

точных временных слоях рассчитываются для обеих границ как

ц'

+0>5

0,5 (ц'

+ ц') -1 Д

(

- ц'). (4.17)

При этих условиях метод переменных направлений обеспечива-

ет второй порядок точности, как по пространственным, так и по вре-

менной координате.

Пример 4.3. Решение смешанной краевой задачи методом пе-

ременных направлений. В качестве примера используем краевую

задачу, рассмотренную в предыдущих разделах.

В квадрате [0:1,0:1] решить смешанную краевую задачу

dU d

1Гэ7

э7

при нулевых начальных и граничных условиях:

U(x, у, 0) = 0; U

(О,

y,t)

U(x,0,t)

U(x,l,t)

В соответствии с изложенным выше, дифференциальное урав-

нение записывается в виде двух конечно-разностных:

ic/i

. -c/^ + _

+/j

;

ггГ+0,5

rfrrl+0,5 ,rrt+0,5

1+1 orr'+l , rr'+l

\Ui,j Ui,j )

I"Jtj,

0,5т

каждое из которых является неявным по одному направлению и яв-

ным по другому. При заданных начальных и граничных условиях

последовательно рассчитываются правые части уравнений, после

чего производится решение уравнений с использованием прогонки

по каждой координате (рис. 4.4).

1/(0

1,2

0 0,05 0,1 0,15 0,2 0,25 0,3 0,35 0,4 0,45 t, с

Рис. 4.4. Решение краевой задачи методом

переменных направлений (т

0,001)

Программа решения двумерной краевой задачи с использовани-

ем метода переменных направлений:

nl=17; n2=17; h=l./(nl-l); n=l; nk=500; u0(l:nl,l:n2)=0.;(l:nl,l:n2)=0.;

f(l:nl,l:n2)=0.; f(8:10,8:10)=100.; fl(l:nl,l:n2)=0.; f2(l:nl,l:n2)=0.; dt=0.001;

while n<nk

for i=2:nl-l

for j=2:n2-l

fl(ij)=(uO(i,j+l)-2.*uO(ij)+uO(i,j-l))/h

2+2.*uO(i,j)/dt+f(i,j);

end

for j=2:n2-l

for i=l:nl

a(i)=l./h

2; b(i)=1.0/h

2; c(i)=2.*(l./h

2+l./dt);

end

alf(2)=0.; bet(2)=0.;

for i=2:nl-l

s 1 =c(i)-a(i)*alf(i); alf(i+l)=b(i)/sl; s2=fl(i,j)+a(i)*bet(i); bet(i+l)=s2/sl;

end

u(nl,j>0.;

for i=nl-l:-l:l

u(i j )=alf(i+1) * u(i+1 ,j)+bet(i+1);

end

u0(l:nl,l:n2)=u(l:nl,l:n2);

for i=2:nl-l

for j=2:n2-l

f2(ij)=(u0(i+l ,j)-2.*uO(ij)+uO(i-l,j))/h

2+2.*uO(ij)/dt+f(ij);

end

for i=2:nl-l

for j=I:n2

a(j)=l./h

2; b(j)=1.0/h

2; c(j)=2.*(l./h

2+l./dt);

end

alf(2)=0.; bet(2)=0.;

for j=2:n2-l

sl=c(j)-a(j)*alf(j);

alf(j+l)=b(j)/sl;

s2=f2(ij)+a(j)*bet(j);

bet(j+l)=s2/sl;

end

u(i,n2)=0.;

for

j=n2-l:-l:l

u(ij)=alf(J+l)*u(i,j+l)+bet(j+l);

end

u0(l:nl,l:n2)=u(l:nl,l:n2); disp(u0(9,9)); n=n+l;

end

disp (u)

Процедура решения легко программируется, а получаемая точ-

ность решения может быть достигнута за меньшее время при более

крупном временном интервале. Установившиеся значения искомой

функции, полученные при решении краевой задачи, также совпадают

с результатами решения, полученными в предыдущих случаях.

4.3. МЕТОД СУММАРНОЙ АППРОКСИМАЦИИ

Метод переменных направлений является не единственным ме-

тодом решения нестационарных многомерных краевых задач. Более

того, этот метод невозможно применить при числе пространствен-

ных координат более двух, так как при решении трёхмерных краевых

задач не представляется возможным аппроксимация трёхмерных

операторов на двух полуцелых временных слоях. В этом случае

весьма эффективными методами являются методы суммарной ап-

проксимации, называемые методами расщепления по пространст-

венным координатам или локально-одномерными [23, 24, 33].

Локально-одномерный метод подразумевает решение много-

мерных краевых задач в несколько этапов, на каждом из которых

решается наиболее простая краевая задача.

В основе этих методов лежит свойство многомерных операто-

ров, называемое аддитивностью, которое заключается в том, что

погрешность аппроксимации многомерной схемы не превышает

суммы погрешностей на каждом этапе решения краевой задачи. При

этом погрешности решения на каждом этапе могут не соответство-

вать суммарной погрешности решения краевой задачи.

Рассмотрим идею локально-одномерного метода применительно

к решению многомерного уравнения параболического типа. Пусть,

например, электромагнитный процесс описан уравнением

где 0<г<?

- время решения задачи; U(x,y,z, 0)

(x,y,z)~ на-

чальное условие; f/| =\|/(*)- известные условия на границе иссле-

дуемой области, а трёхмерный оператор L записывается в виде

(4.18)

( ъи\ д (

К1— +— Кг

\ 0

J Ох 2\

Используя свойство аддитивности многомерных операторов, пред-

ставим его в виде

L(U) = L

(,U) + L

( T/) + L,(T/),

(4.20)

где

°Xl °xij д

Хг

К,

ди

>хг)

0x3

К,

ди

>хг)

(4.21)

Аналогично представим правую часть дифференциального урав-

нения (4.18) на каждом временном интервале в виде суммы трёх

функций, удовлетворяющих условию

f(x,t)

/,(*,/)

С*,0

(x,t),

(4.22)

причём разбиение f(x,t) может быть произведено произвольно.

Для решения уравнения каждый временной интервал разбива-

ется на р частей, соответствующих числу пространственных коор-

динат (в данном случае р = 3), и вводятся временные слои

i+a/l>

= + ах

; а = 1,2,..., р; %

- время, соответствующее одной

части временного интервала.

На каждом временном слое решается одномерное дифференци-

альное уравнение

1 dU _ д

Р dt дхо

К А

дх

+ f

,ti), а = 1,2,..., р

или для рассматриваемого случая:

1Э

ди_

3 dt 8JCV

дх

1 dU _ Э ( dU

3 dt

Эу I

Эу

(4.23)

(4.24)

(4.25)

ldU_d( диЛ

(4.26)

Суммирование левых и правых частей этих уравнений даёт исходное

уравнение (4.18). Производные, входящие в уравнение, аппроксими-

руются известным образом:

rjt+x/3 jjt

i,j,k

jl+z/3 _i-r(+t/3 jjt+tn _

r(+t/3

„m/3

'+U,fc U ЛМ

„r+т/з

'.M

U i-l,j.k

I,(+0,5 Л 1,1-0,5

hx h

(4.27)

1+Х/3,

r<+2x/3

r(+T/3

tVi.M

~~Ui,j,k

/ly

тг'+2т/3

_>,/+2T/3

„<+2т/3

'.J+l.t i.M

2,j+0,5

,г(+2т/3

_ jjt+гхП

yi+гхП U hi,к U i,j—l,k

2,y-0,5

;

(4.28)

W+2T/3.

l+x

(+2x/3

С/ ~U

i,j.к

Лг

trt+x

К ЗД+0,5

i.M+l

'.M

„(+т

U i.j,k

ЛЗД-0,5 ~~

С/

(4.29)

+ /S

Каждое из уравнений (4.27), (4.28), (4.29) после преобразований

может быть представлено в виде системы трёхчленных алгебраиче-

ских уравнений, решаемых методам прогонки вдоль одной коорди-

наты. Так, для уравнения (4.27) решение системы трёхчленных урав-

нений производится вдоль координаты i для всех значений

j =

2,..., JV

; к = 1,2,..., N

. Аналогично, уравнение (4.28) решает-

ся по координате j для значений i = 1,2,..., к =1,2,..., N

а уравнение (4.29) - по координате к для i -1,2,..., N{, j

1,2,..., N