Беляев Е.Ф., Шулаков Н.В., Дискретно-полевые модели электрических машин, учебное пособие

Подождите немного. Документ загружается.

В качестве примера решения двумерной краевой задачи конеч-

но-разностным методом рассмотрим приведённое выше решение

уравнения Пуассона.

Пример 5.2. Решение двумерной краевой задачи конечно-раз-

ностным методом. В квадрате [0:1,0:1] решим стационарную крае-

вую задачу

U d

Эг

•

= /(*,

У)

1х' ду

при нулевых граничных условиях

U( 0, у) = U(

у) = U(x,0)

U(x,

1) =

Примем при решении краевой задачи ту же плотность источни-

ков , что и в примере 5.1.

Пространственные координаты х и у разбиваем на

= 16

интервалов величиной h

l/N

0,0625 .

Дифференциальные операторы аппроксимируем конечно-раз-

ностными выражениями и после преобразования получим систему

алгебраических уравнений:

AuUi-u

BijU

,j + CuUij-1 +

+DijU ;j+i

—

Ei,jU i,j

F i,ji

j = l,2,...,iV

-l,

где A.

=B,

uj=

> ^ij

fijh

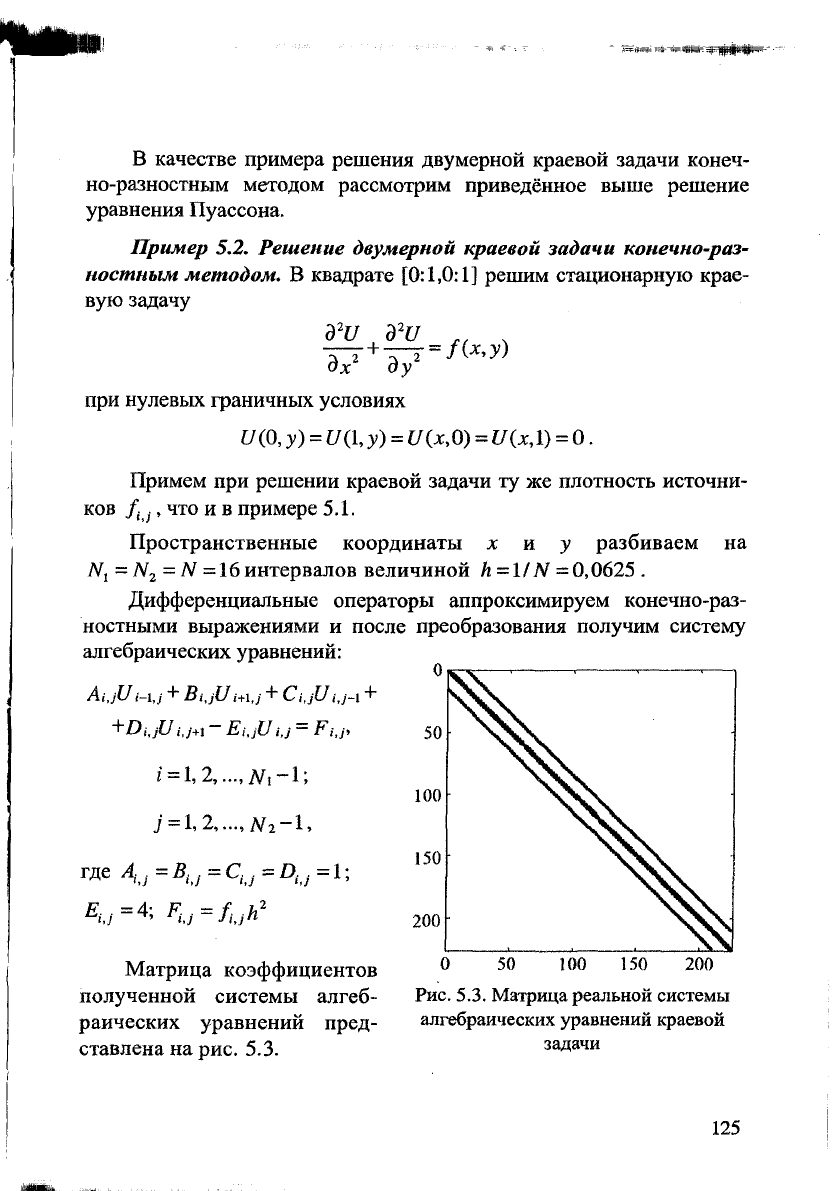
Матрица коэффициентов

полученной системы алгеб-

раических уравнений пред-

ставлена на рис. 5.3.

200

Рис. 5.3. Матрица реальной системы

алгебраических уравнений краевой

задачи

Полученную систему алгебраических уравнений решаем с исполь-

зованием известных численных методов [29].

Программа решения двумерной краевой задачи конечно-раз-

ностным методом:

nl=17; п2=17; dn=16;

hx=17(nl-l);

hy=17(n2-l); dfc=0.001;

a(l:225,l

:225)=0;

f(l:225)=0;

f(97:99)=- 100.*hx

2; f(112:114)=-100.*hx

2; f(127:129)=-100.*hx

2; il=17; i2=29;

while il<212

for i=il:i2

a(i,i-15)=l.; a(i,i-l)=l.; a(i,i)=-4.; a(i,i+l)=l.; a(i,i+15)=l.;

end

il=il+15; i2=i2+15;

end

for i=16:15:196

a(i,i-15)=l.; a(i,i)=-4.; a(i,i+l)=l.; a(i,i+15)=l.;

end

for i=30:15:210

a(i,i-15)=l.; a(i,i-l)=l.; a(i,i)=-4.; a(i,i+15)=l.;

end

for i=2:14

a(i,i-l)=l.; a(i,i)=-4.; a(i,i+l)=l.; a(i,i+15)=l.;

end

for i=212:224

a(i,i-15)=l.; a(i,i-l)=l.; a(i,i)=-4.; a(i,i+l)=l.;

end

a(l,l)=-4.; a(l,2)=l.; a(l,16)=l.; a(15,15)=-4.; a(15,14)=l.; a( 15,30)= 1.;

a(211,212)=l.; a(211,211)=-4.; a(2U,196)=l.; a(225,225)=-4.;

a(225,224)=l.; a(225,210)=l.;

x=f/a;

disp(x);

Результаты решения краевой задачи приведены в табл. 5.6.

Результат решения краевой задачи конечно-разностным методом

совпадает с результатом её решения методом разделения переменных.

При высоких порядках системы алгебраических уравнений их

решение прямыми методами требует значительных затрат машинно-

го времени. Для решения подобных систем более рациональными

являются итерационные методы, позволяющие упростить процесс

решения, уменьшить занимаемую память, а в ряде случаев сократить

время решения.

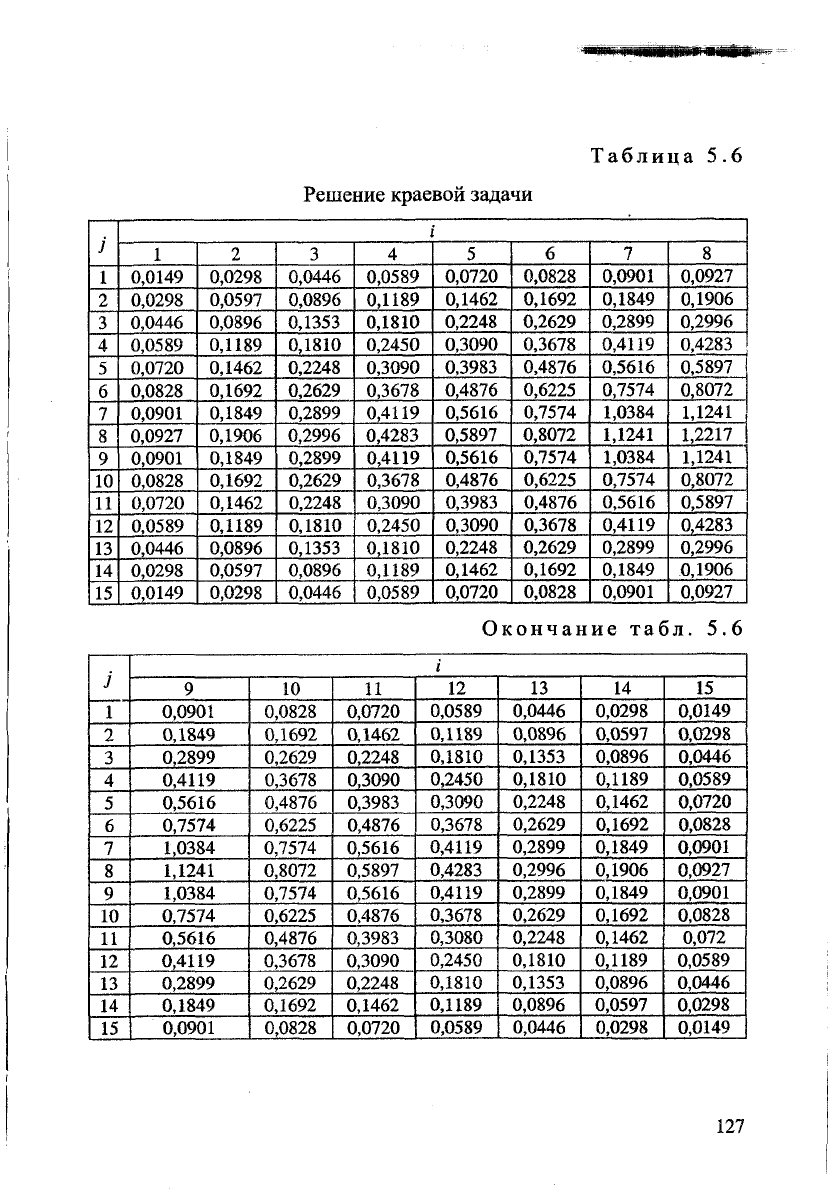
Решение краевой задачи

2 3 4 5

6 7 8

0,0149 0,0298 0,0446

0,0589 0,0720 0,0828

0,0901 0,0927

0,0298 0,0597

0,0896

0,1189

0,1462 0,1692 0,1849 0,1906

0,0446 0,0896

0,1353 0,1810

0,2248 0,2629

0,2899 0,2996

0,0589 0,1189

0,1810 0,2450

0,3090 0,3678 0,4119 0,4283

0,0720 0,1462

0,2248 0,3090

0,3983 0,4876 0,5616 0,5897

0,0828 0,1692

0,2629 0,3678

0,4876 0,6225

0,7574 0,8072

0,0901 0,1849

0,2899 0,4119

0,5616 0,7574 1,0384

1,1241

0,0927 0,1906

0,2996 0,4283

0,5897 0,8072

1,1241 1,2217

0,0901 0,1849

0,2899

0,4119

0,5616

0,7574 1,0384

1,1241

0,0828

0,1692 0,2629

0,3678

0,4876

0,6225

0,7574

0,8072

0,0720 0,1462

0,2248 0,3090

0,3983 0,4876 0,5616

0,5897

0,0589

0,1189

0,1810 0,2450

0,3090 0,3678 0,4119 0,4283

0,0446

0,0896

0,1353 0,1810

0,2248 0,2629 0,2899

0,2996

0,0298 0,0597

0,0896 0,1189

0,1462 0,1692 0,1849

0,1906

0,0149 0,0298

0,0446 0,0589

0,0720 0,0828

0,0901 0,0927

Окончание табл.

5.6

9 10 И

12 13

14 15

0,0901 0,0828 0,0720

0,0589 0,0446 0,0298

0,0149

0,1849 0,1692 0,1462

0,1189

0,0896

0,0597 0,0298

0,2899 0,2629 0,2248

0,1810 0,1353

0,0896 0,0446

0,4119 0,3678 0,3090

0,2450 0,1810

0,1189 0,0589

0,5616 0,4876 0,3983

0,3090 0,2248

0,1462 0,0720

0,7574 0,6225 0,4876

0,3678 0,2629 0,1692

0,0828

1,0384 0,7574 0,5616

0,4119

0,2899

0,1849 0,0901

1,1241 0,8072 0,5897

0,4283 0,2996 0,1906

0,0927

1,0384 0,7574 0,5616

0,4119 0,2899 0,1849

0,0901

0,7574

0,6225

0,4876 0,3678 0,2629

0,1692 0,0828

0,5616 0,4876 0,3983

0,3080

0,2248

0,1462

0,072

0,4119

0,3678 0,3090 0,2450 0,1810

0,1189 0,0589

0,2899 0,2629 0,2248

0,1810

0,1353

0,0896

0,0446

0,1849 0,1692 0,1462 0,1189 0,0896 0,0597

0,0298

0,0901 0,0828

0,0720 0,0589 0,0446

0,0298 0,0149

Простейшим итерационным методом решения систем алгебраи-

ческих уравнений, аппроксимирующих краевые задачи, является ме-

тод Якоби [25]. Для двумерного уравнения (5.29) итерационный про-

цесс записывается в виде

^+0.5,/

^7-0,5,/ Ki,j+0,5 + Kuj-0,5

к;

Яи

TTt+l

l+0,5.j

'J ~ jf

M,j'

(5.31)

'-0,5,/ j ft

"U+0,5

jjt

\j-0,:5

•

--" (J 4-

U+1

Ih~AP

где t - номер итерации.

Это выражение можно формально записать следующим образом:

1+1

-U'

Т а=1

где т =

Км ,

;

+ К:

1+0,5,/ ' (-0,5,/ ^ (,/'+0,5 ' (',/-0,5

-1

ft?

/г,

(5.32)

(5.33)

Большинство итерационных методов можно символически за-

писывать в виде

-U'

в,- —

AU' =-/,

(5.34)

где В, - произвольно выбранный оператор.

Отсюда следует, что итерационный процесс можно рассматри-

вать как разностную схему, соответствующую нестационарной зада-

че. Следовательно, для его реализации могут быть использованы

рассмотренные ранее методы решения нестационарных краевых за-

дач. В качестве оператора В можно использовать любой оператор,

позволяющий быстро находить значения искомой функции if

и обеспечивающий быстрое затухание начальных данных. К таким

операторам можно отнести операторы, используемые при решении

нестационарных задач продольно-поперечным и локально-одномер-

ным методами.

В отличие от нестационарных краевых задач продольно-попе-

речные и локально-одномерные схемы реализуются таким образом,

чтобы необходимая точность решения достигалась за минимально

возможное время. В качестве примера рассмотрим решение стацио-

нарной краевой задачи с использованием продольно-поперечной

схемы.

Пусть решается рассмотренная в примере 5.2 стационарная

краевая задача.

Аппроксимируя дифференциальные операторы конечно-разност-

ными выражениями, запишем дифференциальное уравнение в виде

Для решения задачи итерационным методом представим запи-

санное уравнение как уравнение нестационарной задачи (5.32):

Полученное уравнение решается методом переменных направ-

лений с учётом заданных граничных условий и принимаемых нуле-

выми начальных условий. Величина временного интервала для

неявной схемы выбирается максимальной, обеспечивающей дости-

жение необходимой точности за минимальное число итераций

(Д* =

0,1

против 0,001 при решении нестационарной задачи в при-

мере 3.4).

Результаты итерационного процесса представлены в табл. 5.7,

где приведены значения искомой функции в центре исследуемой

области, а также на рис. 5.4, где показана зависимость искомого

решения в одной из точек исследуемой области U (N) от числа

итераций N . Как видно из таблицы, для достижения необходимой

MJ ~

At h

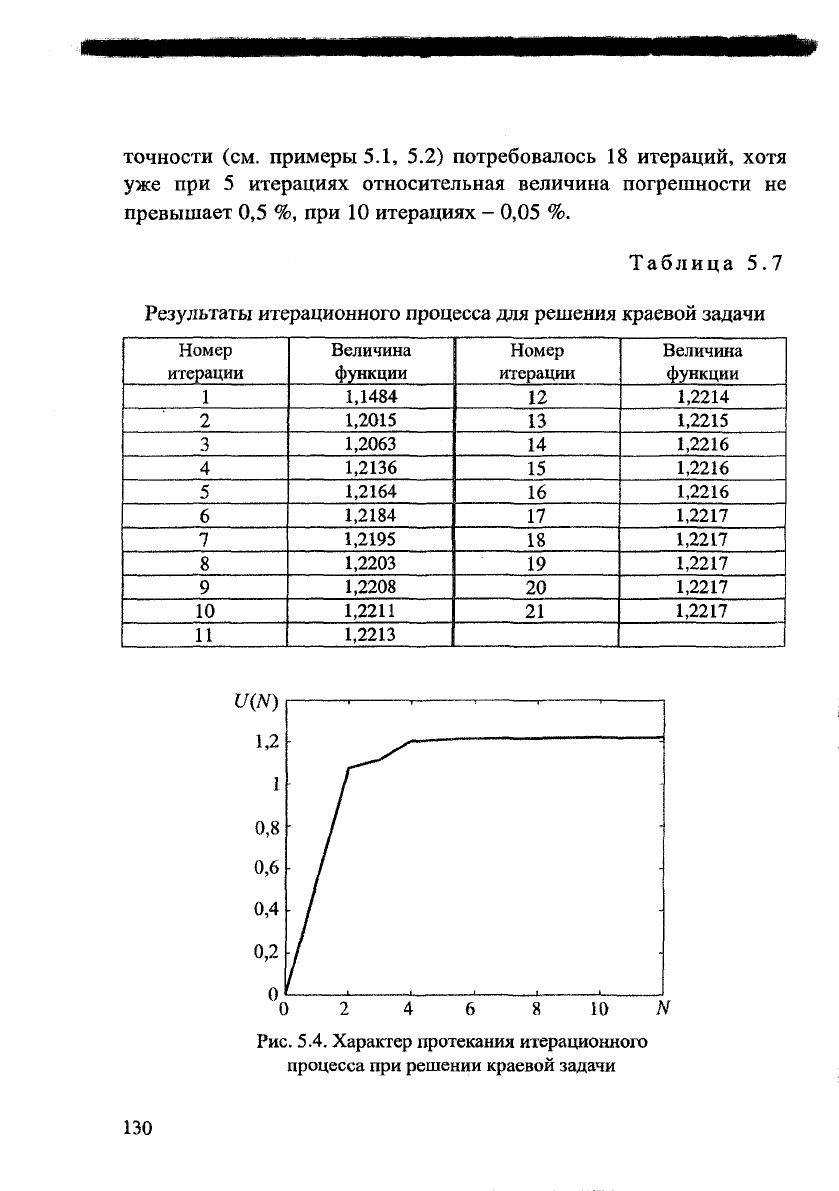
точности (см. примеры 5.1, 5.2) потребовалось 18 итераций, хотя

уже при 5 итерациях относительная величина погрешности не

превышает 0,5 %, при 10 итерациях - 0,05 %.

Таблица 5.7

Результаты итерационного процесса для решения краевой задачи

Номер

Величина

Номер

Величина

итерации функции итерации

функции

1,1484

1,2214

1,2015

1,2215

1,2063

1,2216

1,2136

1,2216

1,2164

1,2216

1,2184

1,2217

1,2195

1,2217

1,2203

1,2217

1,2208

1,2217

1,2211

1,2217

1,2213 |

Рис. 5.4. Характер протекания итерационного

процесса при решении краевой задачи

Рассматриваемая задача может быть решена с использованием

локально-одномерного метода. Однако в этом случае для достижения

необходимой точности приходится уменьшать величину временного

интервала и увеличивать число итераций, так как простейшие схемы

метода обладают первым порядком точности.

6. ВАРИАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ

КРАЕВЫХ ЗАДАЧ

Конечно-разностные методы предполагают замену дифферен-

циального уравнения системой алгебраических путём аппроксима-

ции дифференциальных операторов конечно-разностными выраже-

ниями. Однако такой подход не является единственно возможным.

Альтернативный способ получения системы алгебраических урав-

нений - представление решения краевой задачи в виде разложения

по системе базовых функций, удовлетворяющих заданным гранич-

ным условиям.

Аналогичный случай рассматривался ранее при решении урав-

нения Пуассона методом разделения переменных. Однако в отличие

от этого метода собственные значения и собственные функции диф-

ференциального оператора в общем случае неизвестны. Поэтому ко-

эффициенты разложения не могут быть рассчитаны с использовани-

ем простейших выражений. Их определение связано с решением сис-

темы алгебраических уравнений, получаемой для различных методов

из определённых условий.

Показано [32, 33, 34], что решение краевой задачи с заданными

граничными условиями эквивалентно поиску минимума функциона-

ла определённого вида. Эти вопросы рассматриваются разделом ма-

тематики, называемым вариационным исчислением. Напомним, что

функционалом называется объект математики, когда каждой из мно-

жества функций, принадлежащих этому объекту, может быть постав-

лено в соответствие определённое число.

Для решения задач вариационного исчисления, в частности на-

хождения минимума функционала, наиболее часто используются при-

ближённые методы, к которым относятся методы Ритца и Бубнова-

Галёркина. Эти методы так же, как и конечно-разностные, приводят

к системе алгебраических уравнений, решаемых известными метода-

ми. Однако в отличие от последних методов система уравнений нахо-

дится из условия:

- минимума функционала, если используется метод Ритца;

- ортогональности невязки уравнения к базовым функциям раз-

ложения, если используется метод Галёркина.

Метод Ритца применим для решения краевых задач с самосопря-

жёнными и положительно определёнными операторами дифференци-

альных уравнений.

Напомним, что самосопряжённым уравнением называется диф-

ференциальное уравнение, записываемое в виде

К самосопряжённому виду путём определённых преобразований

может быть приведено любое линейное дифференциальное уравнение

второго порядка [34]

Дифференциальное уравнение считается положительно опреде-

лённым, когда все собственные значения дифференциального опера-

тора уравнения положительны.

Идея метода Ритца сводится к следующему. Пусть функционал

J (и) в области D с граничными условиями на контуре Г, ограничи-

вающем эту область,

(6.1)

(6.2)

и =

tp(x,

у) на Г (6.3)

записывается в виде

J (и) = J]>(x, у,

и, и'

, и'

)dxdy . (6.4)

Как указывалось выше, решение краевой задачи соответствует

поиску минимума этого функционала.

Будем считать, что решение и представляется в виде разложе-

ния по системе пробных функций различного вида, удовлетворяю-

щих заданным граничным условиям. Чаще всего в качестве пробных

функций используют степенные или тригонометрические ряды с не-

определёнными коэффициентами:

H(jc,y)

0(x, y,c

,...,c

). (6.5)

Подставляя указанное разложение (6.5) в выражение функцио-

нала (6.4), выполняя дифференцирование, интегрирование и другие,

соответствующие функционачу математические преобразования, по-

лучим выражение, представляющее определённую функцию коэф-

фициентов разложения с,, с

,..., с

/ = /(с,,с

,...,с

). (6.6)

Для нахождения минимума функционала необходимо прирав-

нять производные полученного выражения по искомым коэффициен-

там нулю:

^- = 0, £ = l,2,...,w, (6.7)

Ъс

в результате чего получаем относительно их систему алгебраических

уравнений. Решение этой системы позволяет определить коэффици-

енты разложения и восстановить решение краевой задачи (6.5).

В ряде конкретных задач решение может быть упрощено, если

пробные функции являются линейными относительно искомых ко-

эффициентов разложения, вследствие чего уравнения системы (6.7)

оказываются первой степени, и для получения необходимой точно-

сти число уравнений может быть относительно небольшим.

В методе Галёркина решение краевой задачи также ищется в ви-

де разложения (6.5), а система алгебраических уравнений определя-

ется из условия ортогональности невязки уравнения краевой задачи.

Если, например, уравнение краевой задачи с однородными гранич-

ными условиями записано в виде

Ци)

Пх,у), (6.8)

решение краевой задачи представлено в виде разложения

"(*>

у)

X у), (6-9)

/=1

где L - дифференциальный оператор;

срДх,

у) - выбранная система

базовых функций, то условие ортогональности имеет вид

J J[Lm(x,

у) - f(x, у)]ф,(х, y)dxdy =

Jjl

Z Cj<Pj(x,y)-f(x,y)

ф,.(х,

y)dxdy

= О,

D\ М

l,2,...,n, (6.10)

или

Ян

) y">

dxd

= JJ/(*> )0ф,-(*>

y)dxdy. (6.11)

D V ;'=I )

Опять получаем систему алгебраических уравнений, позволяю-

щую определить коэффициенты разложения q и восстановить иско-

мую функцию и(х, у).

Недостатком рассмотренных «классических» способов решения

краевых задач является сложность их реализации для получения не-

обходимой точности. Поэтому в настоящее время эти методы совер-

шенствуются с целью упрощения построения системы алгебраиче-

ских уравнений. Основная идея совершенствования - использовать

в качестве базовых функций функции с финитным (конечным) носи-

телем, т.е. функции, отличные от нуля лишь в окрестности рассмат-

риваемой точки. В этом случае число членов каждого уравнения сис-

темы алгебраических уравнений для коэффициентов разложения бу-

дет определяться числом точек, принадлежащих финитному