Беляев Е.Ф., Шулаков Н.В., Дискретно-полевые модели электрических машин, учебное пособие
Подождите немного. Документ загружается.


^F
4
v
a
A;
i=1
(6.92)
где г - номер треугольника с вершиной в узле № 1; F - функционал,
определяемый выражением (6.68).
Производная по А
{
в каждом элементе соответствует первой
строке системы (6.91). Определим
для первого треугольника
(см. рис. 6.3). Обозначим его вершины, принимая во внимание, что
обход производится против часовой стрелки: / = 1; m = 3; и = 2. Тогда
в соответствии с (6.62), (6.63)
bi
=
yз~У
2
=
0
>
b
m
=
y
2
-y
l
=
~h
y
\
Ъп =
УГУг
=
Ьу,
(6.93)
Ci
= хг ~ хз = h
x
\ с
т
= Х\
~ хг
=
0; с
п
=
хз ~
Xi =
~h
x
- (6.94)
Приведём уравнения системы (6.91) к общему знаменателю
и определим правые части уравнений:
4 PS
тр
£тр/ст _ л.. Уст 1 , 2,
2
/ст , 2,
2
4р—•—Й^у-Ц—«жЯу
3 '34
Первое уравнение из этих уравнений
(6.95)
= (bl + Cl) Al +
{bibm
+
С1Ст)Аз
+
Ч
Э
Ау,
+{b,bn + c,Cn)A2 =
^Y
h2xh
y-
(6.96)
Подставляя в это уравнение значения b,, b
m
, Ь
а
, с,, с
т
, с
п
и вы-
полняя преобразования, получим

=hlA-hlA2^
1
fhlh
1
y
. (6.97)
Аналогичные операции проделаем для всех треугольников с вер-
шиной в узле № 1. Полученные данные сведём в табл. 6.1.
Таблица 6.1
Коэффициенты конечных элементов для узла № 1
Номер
треугольника
I m
n
bm
b„ Cl
Cm Cn
1 1 3 2
0
-h
r
hy
К
0
-hx
2
1 4 3
hy
Л
0
0
К
-h
x
3 1
5 4
К
0
-hy
-К
hx
0
4 1 6 5
0
л,
-hy
-h
x
0
h
x
5
1 7 6
-hy
Av
0 0
-Л,
h
x
6
1 2 7
-h
y
0
А»
К
~h
x
0
В результате получим для всех элементов следующие уравнения:
(6.98)
:
h
2
y
Ai
~
h
2
y
A4 =
^-~-h
2
h
2
;
ч
э
Ау
3
=
(h
2
x
+
h$)Ai ~ h\A$ ~
h
2
y
A4
~ l^^f-hlh
2
y
;
(6.99)
V^iA
:
h
2
x
Ai
~ hi As
=
V-~h
2
xh
2
;
(6.100)
ч
э
Л/5
:
h
2
y
Ai
~ h
2
y
Ai
=
V-~-h
2
x
h
2
;
(6.101)
v
a
A л
- {hi
+
hf) A\ ~ hlAi~
h
2
y
An =
^—^hlh
(6.102)

Суммируя левые и правые части этих уравнений, получим
= ф
х
2
+ h] ) Л - 2h
2
A
2
- 2h
2
y
A
4
- IhlA, -
v х у}
^
у
(6.103)
-2h
2
A, -2\U
a
h)h]
•
Учитывая равенство нулю производных в левой части уравне-
ния, выполняем элементарные преобразования и получаем уравнение
А
4
-2А + А
7
А-2А+А
hx hy
(6.104)
совпадающее с уравнением, полученным конечно-разностным методом.
В качестве примера рассмотрим уравнение Лапласа
Э
2
и д
2
и _
+
=
о, (6.105)
дх ду
решаемое методом конечных элементов в работе [35] в прямоуголь-
ной области [0:2, 0:2] с краевыми условиями:
-ч
и(х,0) = 50; и(х, 2) = 100; -Ао, у)
=
0; -^(2, у)
=
0.
ох ах
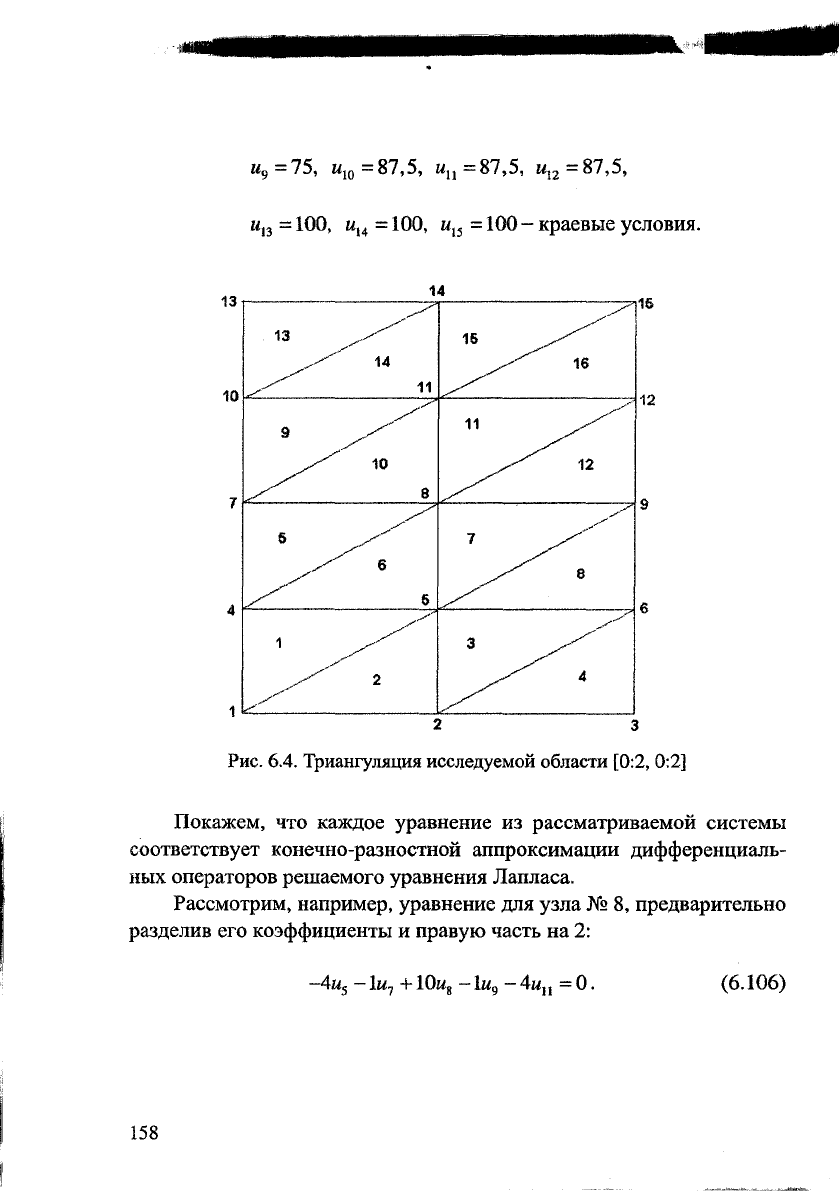
Рассматриваемая область разбита на 16 треугольников с 15 уз-
лами (рис. 6.4).
Система алгебраических уравнений, соответствующая краевой
задаче (6.105), получена в работе [35], записана в матричном виде
(6.107), а её решение представлено ниже:
М[
= 50, и
2
= 50, и
3
= 50 - краевые условия.
и
4
= 62,5, и
5
= 62,5, и
б
=62,5, и
7
=75, м
8
=75,
Ug
—75,
Mjq
—87,5, г/ц —87,5, и^ —87,5,
h,j = 100, м
14
= 100, м
15
= 100 - краевые условия.
13 ^^
^ 14
^^ 11
1В ^^
16
9
^^ 10
8
11
^^
12
б
6
б
7 '
^^ 8
1 ^^
^ 2
3
^^ 4
2 3
Рис. 6.4. Триангуляция исследуемой области [0:2, 0:2]
Покажем, что каждое уравнение из рассматриваемой системы
соответствует конечно-разностной аппроксимации дифференциаль-
ных операторов решаемого уравнения Лапласа.
Рассмотрим, например, уравнение для узла № 8, предварительно
разделив его коэффициенты и правую часть на 2:
-4и
5
-
1и
7
+10щ-
1и
9
- 4м„ = 0. (6.106)
!

1
0
0
0 0
0
0 0 0 0 0 0 0
0
0
«1
50
0
1
0
0 0 0 0 0 0 0
0
0 0
0 0
«2
50
0
0
1
0 0 0 0
0
0 0 0 0 0 0 0
и
3
50
-4
0 0
10
-2
0
-4 0
0
0
0 0
0
0 0
И*
0
0
-8
0 -2 20
-2 0 -8 0 0 0 0 0 0 0
«5
0
0 0 -4
0
-2
10 0
0 -л 0
0 0
0
0 0
и
6
0
0
0
0
-л 0 0 10
-2
0 -4 0 0 0 0 0
щ
0
0
0
0
0
-8
0
-2 20
-2 0 -8 0
0
0 0
Щ
= 0
0 0 0 0 0
-4
0 -2 10 0
0
-4 0
0
0
и
9
0
0
0
0
0 0 0 -4 0 0 10 -2 0
-4
0 0
«10
0
0 0
0
0 0 0 0
-8
0
-2
20
-2 0
-8 0
"11
0
0
0
0
0
0
0 0
0
-4
0
-2 10
0
0
-4
"12
0
0 0
0
0 0 0 0
0
0
0
0 0
1
0 0
"13
100
0 0 0 0 0
0
0 0 0 0 0 0
0
1 0
"14
100
0
0
0
0
0
0
0 0 0 0
0
0 0 0 1
"15
100
(6.107)
Уравнение Лапласа в конечно-разностном виде
ц. .
. — 2м- •
+и , . м -,,
— 2м- •
+и- .
1
i+l,j i,j , <,j+l u]
l,j-l __
hi
Тогда для узла № 8 при h
x
- 1,0 и h
y
= 0,5 получим
и
9
- 2щ
+
щ
+
м
п
_
2м
8
+ и
5
_
Т
2 +
~ '
Выполнив элементарные преобразования, получим уравнение
(6.106).
В ряде случаев энергетический функционал не известен или его
нахождение связано со значительными трудностями. В этом случае сис-
тема алгебраических уравнений может быть получена непосредственно
при интегрировании уравнений Максвелла. Рассмотрим процедуру по-
лучения системы алгебраических уравнений для этого случая.

Согласно определению ротор любого вектора может быть выра-
жен через циркуляцию следующим образом:
dl
ro
tH =
-&
, при
—»
0. (6.108)
dS
Введём векторный потенциал rot А
=
В и запишем уравнение
Максвелла в виде
1 т т
rot—rot A- J .
(6.109)
Интегрируя полученное выражение по произвольной площади
и используя определение ротора, этому выражению можно придать вид
j>—rot Adl
—
^JdS.
L Ц Л'
(6.110)
Таким образом, решение дифференциального уравнения (6.109)
можно свести к системе уравнений (6.110), записываемых для всех
участков площади исследуемой области.
Положим, что исследуемая область разбита на определённое
число элементарных площадок в виде треугольников (триангулиро-
вана), в каждом из которых векторный потенциал является линейной
функцией пространственных координат и записывается в виде
У 2 Ух Аг-Ах
Уъ~У\ Лз-Ai
у-У J
X2~Xi А2-А1
•дез
-
*! Аъ~ А\
= Д - К
х
(л -
) +
К
2
( у - у
1
),
где коэффициенты
(6.111)
_ 1
Kl
~S
У2-У1 А2-А1
У3-У1 А3-А1
л-
7
Х2
-
Xl
А2- Al
хз ~Х\ A3- Al
(6.112)

В этом выражении х
2
,у
2
; х
3
,у
3
-
координаты вершин элементарного тре-
угольника, а Аь Аъ
Аз
- значения векторно-
го потенциала в этих точках.
Если составляющая векторного потен-
циала описывается уравнением (6.66), то со-
ставляющие магнитной индукции в данном
треугольнике будут записываться как
В =
хг ~xi Аг~ Ai
хз ~ х\
Аз
-
Ai
Рис. 6.5. К
выводу
=
Кг
—
const; (6.113) уравнения составляющих
магнитном индукции
Я
= Кi = const. (6.114)
У
2
~У1 А2-А1
У3-У1 А3-А1
Для прямоугольного треугольника, изображённого на рис. 6.5,
с координатами (х,, у
{
;
х
2
,у
2
',х
3
,у
3
) будем иметь:
X2~Xl~hx> X3~Xl =
hx>
У
2
-У1
= °>
Уз-У\
= Н
Г
5 =
xi~x\ У
2
~У
хз~х\ У
г
~У\
\x2-xi ){Уз-у)
=
Ь
х
к
у
В =
(хг ~ *I)(
АЭ
~ At)
=
hM _ АА _ ЭА .
В
У =
hxhy hxhy h
y
(Уз~ Ai) _ hM_ АА
hxh
y
h
x
h
Х
Пу
hx
ЭА
дх
(6.115)
(6.116)
(6.117)
т.е. уравнения записываются в том же виде, что и при конечно-
разностной аппроксимации.
Линейный интеграл может быть записан в виде суммы двух ин-
тегралов:
$B dT= ]В
Х
dx
+
B
y
dy. (6.118)

Интегрирование производится по сторонам треугольника, урав-
нения которых представляются в виде уравнений прямых линий. Для
стороны х,у, - х
2
у
2
, например,
х -XI _ У-Ух
=t
(6.119)
Х2-Х1 Уг-^!
или в параметрическом виде
* = x,+(x2-xi )*; y = {y
2
~yi)t- (6.120)
Отсюда
dx
=
(
xi
-xx)df, dy
=
(y
2
-
yi
)dt. (6.121)
Для точки с координатами (х,, у,) величина = 0, а для точки
с координатами (х
2
, у
2
)~
Ц
=1. В этом случае интеграл по стороне
треугольника 1-2 будет иметь вид
2 _ 2 1
\М = \(B
x
dx
+
B
y
dy) = J[fi
t
(x, - X,) + B
y
(y
2
- y,)]. (6.122)
1 1 0
Подставляя в полученное выражение В
х
и В
у
по (6.113), (6.114)
и выполняя интегрирование, будем иметь
2
\Bdl =[к2(хг-х
1
)
+
К
1
(у
2
-у
г
)]. (6.123)
I
Аналогично
3 _
JBdl =К2(хз-х
2
)-К
1
{у
3
-у
2
), (6.124)
2
1
\М =^2(Х1-Хз)-^1(У,-Уз)- (6-1
25
)
3
Рассмотрим изложенный выше подход для решения краевой задачи
(6.105), считая исследуемую область триангулированной (см. рис. 6.3).

Определим коэффициенты Ki и Кг
ДЛЯ
всех треугольников этой
области, используя выражения (6.112). Например, для треугольника № 1:
1
У 5 Ух Us-Ul
У 4 У) U4~Ul
_ hy.
-
Т
(м<
~и.5);
Кг
1
~~(u4~ui)
•
О
(6.126)
U5~Ul
О X4~Xl U4 U\
Обозначая значения искомой функции в узлах соответствую-
щими индексами, выразим коэффициенты уравнения (6.111) через
значения функции в узлах и их координаты. Полученные данные для
всех треугольников сведены в табл. 6.2.
Таблица 6.2
Коэффициенты уравнения (6.111) для краевой задачи (6.105)
Номер
треугольника
Коэффициент
Ki
Коэффициент
K
2
1
h
v
(u
4
-
u
s
)/S h
x
(u4
-
иi)/S
2
h
y
(u\
-
u
2
)/S
h
x
(u
s
-
u
2
)/S
3
A
v
(Ms
-
u
6
)/S
ЬЖщ
-
u
2
)/S
4
/f
v
(«2
-
M
3
)/5
h
x
(u
6
-
u
3
)/S
5
h
y
(u
7
-
ug)/S
h
x
(u
7
-
u
4
)/S
6
h
v
(u
4
-
u
5
)/S h
x
(u
s
-
u
s
)/S
7
h
v
(Ug - Ug)/S
h
x
(u%
-
u5i)/S
8
h
v
(u
s
-
u
6
)/S
h
x
(u
9
-
u
6
)JS
9 h,(u
10
-u
u
)/S
h
x
(u
U)
-
u
7
)/S
10
h,(uy
-
u
s
)/S
h
x
(u
n
-
u
t
)/S
11
h
v
(u
n
-u
l2
)/S h
x
(u „ -
m
8
)/5
12
к^щ -
u
9
)/S h
x
(u
l2
-
u
9
)/S
13
hy(u
l3
-
u
l4
)/S
h
x
{u
n
-
u
l0
)/S
14
h,(u
l0
- u
u
)/S
h
x
(u
l4
- u
u
)/S
15
h
v
(u
H
-
ui$)/S
h
x
(u
l4
-u
n
)/S
16
hfyiu -
u
i2
)/S
h
x
(u
15
-
u
l2
)/S
Выполним интегрирование по поверхности треугольников, ок-
ружающих узлы исследуемой области. Учитывая, что сумма инте-
гралов вдоль смежных сторон треугольников равна нулю, сумма ин-
тегралов будет равна сумме интегралов вдоль наружных сторон мно-
гоугольника, окружающих рассматриваемый узел. Например, для
узла № 4 (см. рис. 6.4)

\(Bjx + B&)= J + J + J + f + f. (6.127)
L 1 5 8 7 4
В указанном выражении для упрощения записи опущены одно-
типные выражения под знаками интегралов.
Согласно краевым условиям на левой границе исследуемой области
4 1
\(вАх + В^у) = 0; \(Bjx + Bjly) = 0. (6.128)
7 4
Оставшиеся интегралы:
5 ,
\(в&
+
B/ty)
=
K
2
{xs -
Xl) +
Ki{y
5
- у,) = -f{u4-м,)(х
5
-
Xl) +
1
2 2
(6Л29)
+ (и4 - Us){y
s
- У,) = у-(м4 -
Ml)
+ - м
5
)-
Аналогично
g 2
|(вд« + в//у) = у(«4-м
5
); (6.130)
iJ
[(яА + Му) = -^(м4-И
7
)- (6.131)
8
Л
С учётом того, что h
x
= 1,0, h
y
= 0,5, S = h
x
h
y
= 0,5, будем иметь
э в
J{Bjx
+
B/y)= \{B^c
+
B/fy)+ \{в/1х
+
в/у)
+
li h
8
(6.132)
+—(M
4
-M
S
)+—(M.-M,) = (M
4
-M,) +
2-
——(u.-uA +
s
V
4 5/
5
v
4 7/
0 5
V 4 I)
a5
V
4 5}
+~-^(u
4
-u
1
)
=
-2u
l
+5u
4
-u
s
-2u
1
.
