Беляев Е.Ф., Шулаков Н.В., Дискретно-полевые модели электрических машин, учебное пособие

Подождите немного. Документ загружается.

<RZR„-, 0 <

< 2л,

где R

R„

- внутренний радиус ротора и наружный радиус статора

асинхронной машины.

В уравнении опущен индекс единственной составляющей век-

торного потенциала и плотности стороннего тока.

Согласно принятым допущениям, магнитная проницаемость р

не зависит от координаты ф и может быть вынесена за знак произ-

водной. Поэтому уравнение в окончательном виде записывается как

1JL

RdR

I I d А .

+ " =-

/ст

. (7.10)

r ц эф

Уравнение (7.10) с нулевыми граничными условиями по коор-

динате R и периодическими условиями по координате ф образуют

двумерную краевую задачу, решение которой определяет магнитное

поле в зазоре и магнитопроводах статора и ротора.

Вводя определённые допущения, можно значительно упростить

задачу, сведя её к одномерной.

Пусть в стационарном режиме система сторонних токов, возбу-

ждающая магнитное поле, и векторный потенциал представляют бе-

гущую вдоль расточки статора волну:

г =

Ji^-w)

•

Л = A

J(<%t-P<f>)

J с J с.м

' Лм

Переходя к комплексным выражениям и выполняя дифференци-

рование по пространственной координате ф, преобразуем уравнение

(7.10) к виду

1 д(„1дА

) р

RdR

R-

р dR

= (7-11)

Яр

Полученное одномерное дифференциальное уравнение решает-

ся конечно-разностным методом.

Постановка краевой задачи и её решение приведено в примере 7.1.

Пример 7.1. Расчёт магнитного поля трёхфазного асинхрон-

ного двигателя. Рассчитать характер распределения магнитного по-

ля вдоль радиальной координаты для трёхфазного асинхронного дви-

гателя по следующим данным:

- начальный радиус 30-Ю

-З

м;

- высота ярма статора и ротора 5

•

-3

м;

- величина воздушного зазора 0,5

• 10~

м;

-магнитная проницаемость материала ярма статора и ротора

= 500ц

;

- число полюсов 2р = 2;

- плотность стороннего тока j

СТМ

= Ю

А/м

Программа решения задачи, реализованная в пакете MATLAB

приведена ниже:

nl=50; ii2=60;

пЗ=1Ю;

n4=160;; mu0=4.*pi*l.e-7;

tok=l.e7;

r0=30.e-3; р=1;; р=1;

hr=0.1e-3; f(l:n4)=0.;f(nl+l:n2)=tok; alf(2)=0,; bet(2)=0.; y(n4)=0;

mu(l:nl)=500.; mu(nl+l:n2)=l.; mu(n2+l:n3)=500.; mu(n3+l:n4)=L;

for i=l:n4+l

r(i)=rQ+hr*(i-l);

end

fori=2:n4-l

a(i)=( 1 ,/mu(i)+l./mu(i-1))*(1 .-0.5*hr/r(i));

b(i)=( 1 ./mu(i)+1 ./mu(i+1))*(1 ,+G.5*hr/r(i));

c(i)=a(i)+b(i)+2.*p

2*hr

2/(mu(i)*r(i)

2); ft(i)=2.*muO*hr

2*f(i);

end

for i=2:n4-l

d=c(i)-a(i)*alf(i); alf(i+l)=b(i)/d; bet(i+l)=(ft(i)+a(i)*bet(i))/d;

end

for i=n4-l:-l:l

y(i)=alf(i+1 )*y(i+1 )+bet(i+1);

end

for i=2:n4-l

br(i)=y(i)/r(i); bf(i)=-(y(i+l)-y(i-l))/(2.*hr);

end

for j=l:n4-l

nn(j)=j;

end

nl(nn)=nn; n2(nn)=10*br; n3(nn)=bf;

disp(abs(bf));

plot(nl,n2,nl,n3)

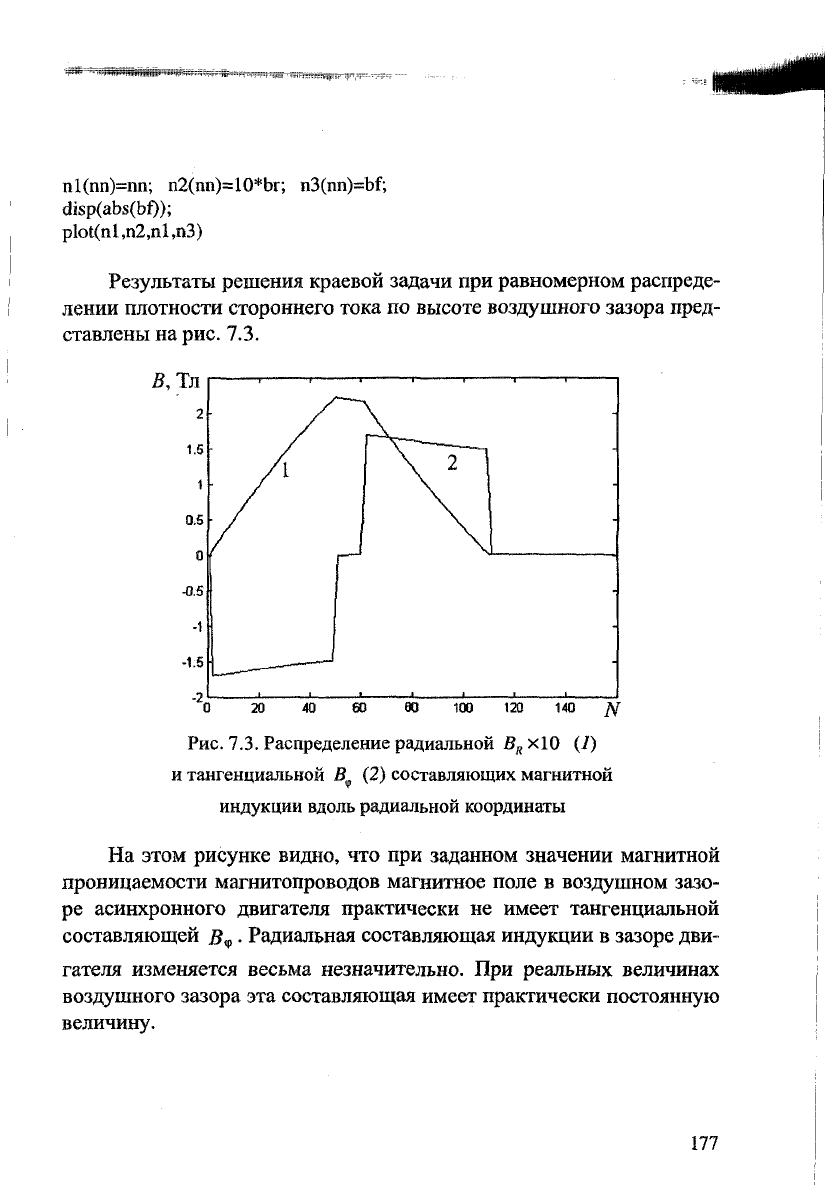
Результаты решения краевой задачи при равномерном распреде-

лении плотности стороннего тока по высоте воздушного зазора пред-

ставлены на рис. 7.3.

Рис. 7.3. Распределение радиальной B

xlO (/)

и тангенциальной В

(2) составляющих магнитной

индукции вдоль радиальной координаты

На этом рисунке видно, что при заданном значении магнитной

проницаемости магнитопроводов магнитное поле в воздушном зазо-

ре асинхронного двигателя практически не имеет тангенциальной

составляющей . Радиальная составляющая индукции в зазоре дви-

гателя изменяется весьма незначительно. При реальных величинах

воздушного зазора эта составляющая имеет практически постоянную

величину.

-ШШ!

Тангенциальная составляющая магнитной индукции в ярме ста-

тора и ротора также имеет малое затухание, а радиальная составляю-

щая изменяется по высоте ярма по закону, близкому к линейному.

Действительно, при выполнении условия непрерывности маг-

нитного потока

R Эф эя

представлении магнитного поля в виде бегущей волны

й = r Д<%<-/><р). д _ л ЛЩ'-РЧ)

DR DRA^ ' tSif Л»ф

и малом изменении радиуса кривизны (R~const) производная

(7.12)

(7.13)

дВк

ЭR

близка к постоянной величине.

Если не принимать во внимание незначительное затухание маг-

нитного поля в ярме статора и ротора, т.е. считать, что тангенциаль-

ная составляющая магнитной индукции распределена равномерно по

высоте ярма (рис. 7.4), то возможно построение расчётной модели,

которая даёт возможность аналитического решения.

Для этого аппроксимируем первый член уравнения (7.9) сле-

дующим образом:

±_L

RdR

IdA

p dR

_LI

4 S

VL^l

p dR J

^ p dR

1 ЭА

(7.14)

Согласно принятому выше допущению, магнитная индукция в

распределена по высоте ярма статора (/г

яс

) и ротора (й

яр

) равно-

мерно, а в воздушном зазоре равна нулю, что показано на рис. 7.4.

Величины магнитных индукций д

и BR выражаются через

векторный потенциал в виде

Sep

дА

1_дА

R Эф

(7.15)

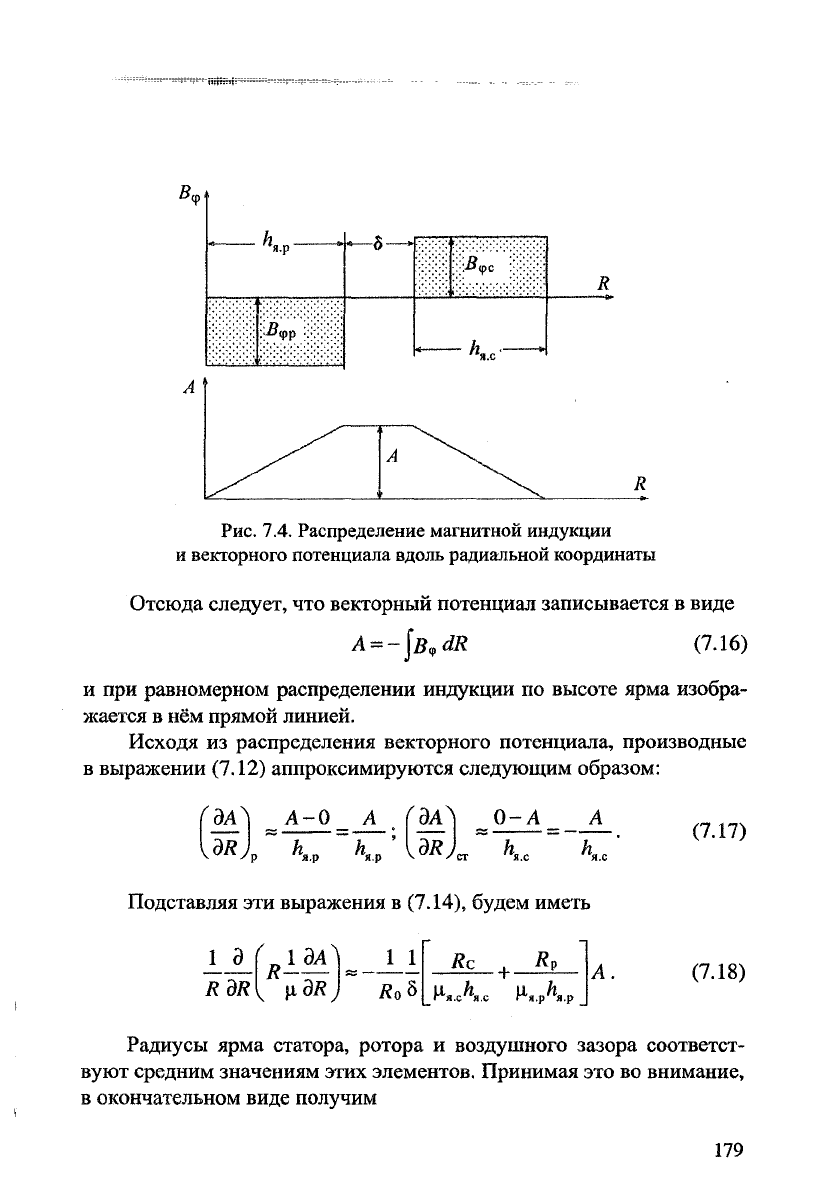
Рис. 7.4. Распределение магнитной индукции

и векторного потенциала вдоль радиальной координаты

Отсюда следует, что векторный потенциал записывается в виде

A = -\B„dR (7.16)

и при равномерном распределении индукции по высоте ярма изобра-

жается в нём прямой линией.

Исходя из распределения векторного потенциала, производные

в выражении (7.12) аппроксимируются следующим образом:

'АО

чЭЯу

А-0 _ А

Кр К.р

алЛ о-л

э/?Л ~

(7.17)

Подставляя эти выражения в (7.14), будем иметь

1JL

RdR

i_dA

цЭR

_LI

Ro $

_ Rp

KpKp

(7.18)

Радиусы ярма статора, ротора и воздушного зазора соответст-

вуют средним значениям этих элементов. Принимая это во внимание,

в окончательном виде получим

1JL

RdR

j_a4

2/?o

-g'A (7.19)

Заменяя первый член двумерного уравнения (7.9) полученным

выражением, приведём его к одномерному:

ЭА

1 1 Э

Р Эф^Эф

-q'A = -j

(7.20)

' J

Векторный потенциал

в этом выражении определён в сере-

дине воздушного зазора. Поэтому в качестве магнитной проницаемо-

сти р необходимо взять проницаемость воздуха р

, а в качестве ра-

диуса - радиус середины воздушного зазора

Ro.

Тогда уравнение

векторного потенциала будет иметь вид

Хо дф

"Ро<7'А = -р

/ст-

(7.21)

Подставляя магнитную постоянную р

в выражение (7.19) и вы-

полняя промежуточные преобразования, получим

5+А.р

2j?p

" v-LKJ

(7.22)

где р

1Х

и р

- относительные магнитные проницаемости материала

ярма статора и ротора.

Одномерное уравнение

J_3fA

Эф

•qA

—р

(7.23)

с учётом граничных условий периодического типа

ЭД ЭД

А(0) = Л(2к); f-(0) =—(2п) (7.24)

Оф Оф

описывает в указанной области векторный магнитный потенциал.

Для решения краевой задачи необходимо задание источников

поля - правой части дифференциального уравнения.

Плотность тока статора в правой части уравнения (7.23) - это

плотность равномерно распределённого в зазоре тока проводников

обмотки статора. Если считать, что в исследуемой области 0 <

< 2л

ток проводника сосредоточен в точке, то его плотность может быть

записана как

/С1(ф) =

в)5(

-ф,.), (7.25)

где /(ф) и Щф) - ток и число витков обмотки статора в функции

пространственной координаты;

ф.

- координата точки расположения

проводника обмотки; 5(ф) - дельта-функция Дирака; 5' - приведен-

ный воздушный зазор.

Поскольку значение дельта-функции неопределенно, то при ис-

пользовании конечно-разностных методов плотность тока на каждом

пространственном интервале может быть определена как среднее

значение:

J^JJM^

(7.26)

tfoA.l R<A-{ § ЗЯоЛф

где /, и W

- ток и число проводников, принадлежащих г-му интер-

валу разбиения пространственной координаты. В полученном выра-

жении учтены свойства дельта-функции.

Следовательно, при известной схеме статорной обмотки (про-

странственном расположении проводников с током), заданной вели-

чине токов и числе витков в фазе обмотки плотность стороннего тока

может быть рассчитана по выражению (7.26).

Краевая задача, описываемая уравнением (7.23), периодически-

ми краевыми условиями (7.24) с источниками магнитного поля (7.26)

решается конечно-разностным способом с использованием цикличе-

ской прогонки (см. часть I, подразд. 3.2.2). Рассчитав значения век-

торного потенциала, можно определить величины составляющих

магнитной индукции в зазоре двигателя, ярме статора и ротора, ис-

пользуя приведённые выше соотношения.

Если плотность стороннего тока представлена в виде бегущей

волны:

(7.27)

где со

= 2л/ - круговая частота сети; р - число пар полюсов; 7

СТ м

комплексная амплитуда плотности тока, то краевая задача может быть

решена аналитически. В этом случае векторный потенциал также пред-

ставляет бегущую волну:

А,=АУ

'""

Р<Р)

- (7-28)

Подставляя это выражение в уравнение (7.23) и выполняя пре-

образования, получим для комплексной амплитуды векторного по-

тенциала следующее решение:

4=% (7.29)

q + a

где коэффициент а =

—

= —; т - полюсное деление двигателя,

т Ro

Комплексная амплитуда магнитной индукции в воздушном за-

зоре двигателя, согласно (7.15)

(7.30)

а в ярме статора и ротора

(7-31)

Ля

™!%ШДЯ1П{ШП!5М

Ниже приводится пример решения краевой задачи численным

и аналитическим методами.

Пример 7.2. Аналитический и численный расчёт магнитного

поля трёхфазного асинхронного двигателя в режиме холостого

хода. Рассчитать магнитное поле (огибающие радиальной и танген-

циальной составляющих магнитной индукции) трёхфазного асин-

хронного двигателя в режиме идеального холостого хода со следую-

щими параметрами:

~ число пар полюсов р = 1;

- полюсное деление т = 0,0942 м;

- воздушный зазор б = 0,0005 м;

- высота ярма статора h

= 0,006 м;

- высота ярма ротора h

= 0,004 м;

- магнитная проницаемость материала ярма статора и ротора

ц = 1000 ц

;

- фазный ток обмоток / =

А;

- число витков в катушке

100;

- схема обмотки:

а) однослойная

А А

Z Z В в X X с с

Y Y

б) двухслойная

А Z Z в в X

X с

Y Y

А Z Z в в X X

с с

Y Y А

Расчёты магнитного поля произвести для однослойной и двух-

слойной обмоток.

Сравнить результаты моделирования с аналитическим решени-

ем при задании токовой нагрузки в виде бегущей волны.

Решение. Магнитное поле машины в одномерном приближении

описывается дифференциальным уравнением (7.23) с периодически-

ми краевыми условиями, где величина q определена выражением

(7.22).

Для решения краевой задачи исследуемая область [0, 2rt] разби-

вается на N = 120 интервалов величиной

ф =

2Е

МИ

0,05236.

N 120

Средний радиус

рх 1-0,0942

= —=

= 0,03 м.

л 3,14

Комплексная амплитуда плотности равномерно распределённо-

го по высоте зазора тока статора записывается в виде

j^^bii, IdliiO / «1,8-10

•/. (А/м

АфRJ> 0,05236-0,03-0,0005 ' ' \ 7

где i - номер интервала разбиения пространственной координаты.

Коэффициент

{ |

/г

С1

+§

/г

+ 5

0,006 + 0,0005

2-0,03

ц'

яс

ст

5 ц'„А

1000-0,006-0,0005

}

0,004 + 0,0005

+ ^^ = 831,9437 м"

1000-0,004 0,0005

Дифференциальный оператор уравнения магнитного поля ап-

проксимируется конечно-разностным выражением, и краевая задача

сводится при этом к системе трёхчленных алгебраических уравне-

ний, решаемых методом циклической прогонки.

Система алгебраических уравнений записывается в виде

у,_1

-с,у, + В,у

-/,; i = 1, 2, 3,..., N-l, N,

коэффициенты которой: Д = 1; В, = 1; С, = 2 + qRlA<p

= 2,2238 ;

(

= Мег/ЯоАф

= 0.005583 •/,.