Беляев Е.Ф., Шулаков Н.В., Дискретно-полевые модели электрических машин, учебное пособие

Подождите немного. Документ загружается.

При задании токовой нагрузки по отдельным интервалам сле-

дует учесть, что система токов статора является трёхфазной и по-

этому токи должны быть записаны в комплексной форме. Ком-

плексы фазных токов двигателя: /

= 1,0 А ; i

=(-0,5- j 0,866) А;

=(-0,5 + j-0,866)А, а их пространственное распределение со-

ответствует схеме обмотки двигателя.

Решая систему алгебраических уравнений методом циклической

прогонки, можно определить значения векторного потенциала во

всех точках исследуемой области. В результате расчета значений

векторного потенциала определяются комплексы магнитной индук-

ции в зазоре, ярме статора и ротора двигателя по выражениям (7.30)

и (7.31). Величины составляющих магнитной индукции находятся

как модули соответствующих комплексов.

Для численного решения использована программа, реализован-

ная в пакете MATLAB:

n=120;

р=1;

del=5.0e-4; tau=0.0942; hs=6.0e-3; hr=4.0e-3; pr0=4.*pi*1.0e-7;

prs= 1000.0; prn=1000.0; tok=1.0; wk=10.0; h=2.*pi/n; r0=p*tau/pi;

r 1 =(hs+del)/(2.

*r0);

dl=r0*h; d2=dl*dl; r2=(hr+del)/(2.*r0);

r3=(l.+rl)/(prs*del*hs); r4=(l.-r2)/(prr*del*hr); q=r3+r4; ta=l.; tb=tok*(-0.5-0.866i);

tc=tok*(-0.5+0.866i);

f(l:20)=ta; f(21:40)=-tc; f(41:60)=tb; f(61:80)=-ta; f(81:100)=tc; f(101:120)=-tb;

a(l:n)=l.; b(l:n)=l.

;

c(l:n)=2.0+q*d2; ft(l:n)=1.4142*f(j)*wk*dl*pr0/del;

alf(l)=0.; bet(l)=0.; gam(l)=l.;

for j=l:n

d3=c(j)-a(j)*alf0); alf(j+1 )=b(j)/d3; bet0+l)=(ft(j)+a(j)*bet(j))/d3;

gam(j+ l)=a(j)*gam(j)/d3;

end

u(n- l)=bet(n); v(n-1 )=alf(n)+gam(n);

for j=2:n-l

k=n-j; u(k)=alf(k+1 )*u(k+1 )+bet(k+1); v(k)=alf(k+1 )*v(k+1 )+gam(k+1);

end

d5=bet(n+1 )+alf(n+1 )*u( 1); d6=

,-alf(n+1) *v( l)-gam(n+1); у(n)=d5/d6;

у (1 :n-1 )=u( 1 :n-1 )+y (n)*v(

:n-1);

br(l)=(y(2)-y(n))/(2.*h*r0); br(n)=(y(l)-y(n-l))/(2.*h*r0);

for j=2:n-l

br(j)=(y(j+l)-y(j-l))/(2.*h*r0);

end

for j=l:n

bf(j)=y(j)/hs; brs(j)=abs(br(j));

bfs(j)=abs(bf(j)>; js(j)=j;

ss(j)=0.;

end

disp(abs(bf)); plot(js,bfs js,ss)

Если обмотку статора выполнить двухслойной с укорочением,

то амплитуды высших пространственных гармоник уменьшаются

и форма МДС приближается к синусоиде. Программа расчёта маг-

нитного поля при этом остаётся прежней, за исключением числа вит-

ков в катушке, которое уменьшается в 2 раза, и пространственного

распределения токовой нагрузки статора, принятого в соответствии

с двухслойной схемой.

Результаты численного решения задачи для машины с однослой-

ной обмоткой представлены в табл. 7.1 и 7.2, а распределение ради-

альной и тангенциальной составляющих магнитной индукции в воз-

душном зазоре и ярме статора - на рис. 7.5. Аналогичные результаты

для машины с двухслойной обмоткой представлены в табл. 7.3 и 7.4

и на рис. 7.6.

Таблица 7.1

Распределение радиальной составляющей магнитной

индукции в зазоре двигателя для однослойной обмотки

(огибающая значений)

Номер точки

Br, ТЛ

Номер точки Яя.Тл

0,4237

0,3394

0,4075

0,3414

0,3928

0,3453

0,3798

0,3512

0,3685

0,3589

0,3685

0,3512

0,3798

0,3453

0,3928

0,3414

0,4075

0,3394

0,4237

Далее значения функции повторяются.

fr J^

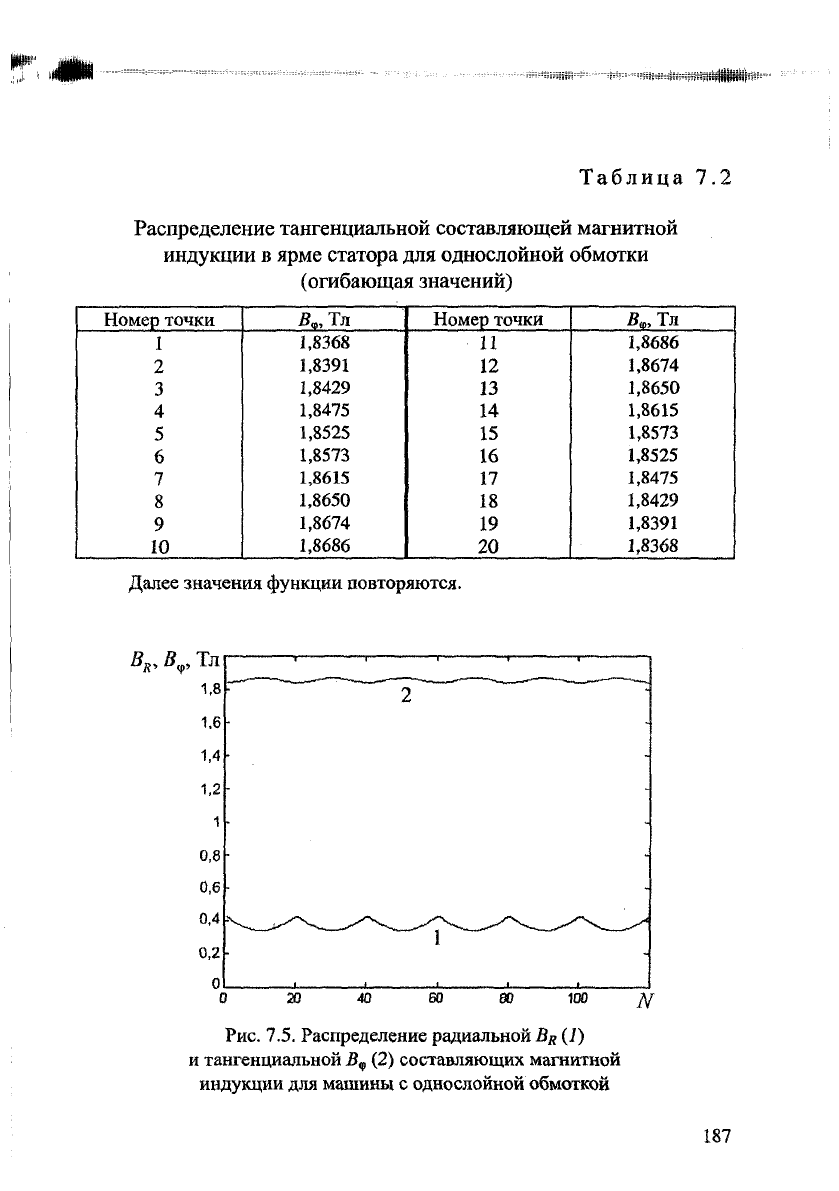
Распределение тангенциальной составляющей магнитной

индукции в ярме статора для однослойной обмотки

(огибающая значений)

Номер точки

Тл Номер точки

Тл

1,8368

1,8686

1,8391

1,8674

1,8429

1,8650

1,8475

1,8615

1,8525

1,8573

1,8525

1,8615

1,8475

1,8650

1,8429

1,8674

1,8391

1,8686

1,8368

Далее значения функции повторяются.

Рис. 7.5. Распределение радиальной B

(1)

и тангенциальной B

(2) составляющих магнитной

индукции

для

машины с однослойной обмоткой

Таблица 7.3

Распределение радиальной составляющей магнитной

индукции в зазоре двигателя для двухслойной обмотки

(огибающая значений)

Номер точки

Тл

Номер точки

Тл

0,3682

0,3632

0,3602

0,3587

0,3542

0,3557

0,3501

0,3541

0,3481

0,3541

0,3481

0,3557

0,3501

0,3587

0,3542

0,3633

0,3602

0,3693

0,3682

0,3693

Далее значения повторяются.

Вir Др, Тл

1,8

1,6

1.4

1,2

0,8

0,6

0,4

0,2

0 20 40 60 80 100 д г i

Рис. 7.6. Распределение радиальной В

(1)

и тангенциальной

(2) составляющих магнитной

индукции для машины с двухслойной обмоткой

Распределение тангенциальной составляющей магнитной

индукции в ярме статора для двухслойной обмотки

(огибающая значений)

Номер точки

ffl

, Тл Номер точки

В®,

Тл

1,7913

1,7856

1,7945

1,7841

1,7971

1,7831

1,7991

1,7827

1,8000

1,7827

1,8000

1,7831

1,7991

1,7840

1,7971

1,7856

1,7945

1,7879

1,7913

1,7879

Далее значения повторяются.

Характер распределения магнитной индукции в воздушном за-

зоре двигателя с двухслойной обмоткой статора наглядно свидетель-

ствует об уменьшении амплитуды высших пространственных гармо-

ник МДС.

При задании токовой нагрузки в виде бегущей волны возможно

аналитическое решение задачи, записываемое в виде (7.29):

д _ И'О J ст

a+q

Здесь коэффициенты а = 831,9437 м

-2

; а =

—

= = 33,35 м

-1

т 0,0942

Амплитуда плотности стороннего тока в этом случае рассчиты-

вается через значения линейной токовой нагрузки:

AS =

mW^K^l 3-200 0,966 1,0

рт 1-0,0942

: 6152,866 А/м.

5 0,0005

В этих выражениях т - число фаз; - число витков фазной об-

мотки; Кф - обмоточный коэффициент для первой гармоники; I - фаз-

ный ток статора.

Амплитуда векторного потенциала

_. 4л-10~

1,735 10

-Q Q22214B6/m.

a +q 33,35

+831,9437

Амплитуда радиальной составляющей магнитной индукции в воз-

душном зазоре двигателя

Br =

= 33,35

•

0,011214 = 0,374 Тл.

Амплитуда тангенциальной составляющей магнитной индукции

в ярме статора

her "10

Сравнение результатов моделирования и аналитического реше-

ния свидетельствуют о близости их значений.

Используя данные примера, проанализируем влияние насыщения

магнитопровода статора и ротора на величину магнитного поля двига-

теля в режиме идеального холостого хода. При насыщении магнито-

провода величину относительной магнитной проницаемости материа-

ла ярма статора и ротора примем: ц

= ц

= 250 |х

Коэффициент q в этом случае составит

Ih±l i

/г

+ 6

| 0,006 + 0,0005

2-0,03

ц'я.Л

250-0,006-0,0005

0,004 + 0,0005

^^ = 3327,8 м-

250-0,004-0,0005

Амплитуда векторного потенциала

-1,735-1С

a+q 33,35

+3327,8

М^

-10-М,735-10-

= вб/м

2 , „ ц 1С

а амплитуды радиальнои и тангенциальной составляющих магнитнои

индукции в зазоре и ярме статора двигателя соответственно составят:

=аА = 33,35

•

0,00491 = 0,1637 Тл;

А 0,00491

П010Т

Полученные результаты показывают, что насыщение магнито-

провода влияет на величину магнитной индукции в зазоре двигателя.

Снижение проницаемости материала магнитопроводов статора и ро-

тора, возникающее при их насыщении, приводит к существенному

уменьшению магнитной индукции в зазоре двигателя.

73. УЧЁТ НАСЫЩЕНИЯ МАГНИТОПРОВОДА

АСИНХРОННОГО ДВИГАТЕЛЯ

Рассмотренный выше пример показывает, что величина магнит-

ного поля в зазоре асинхронной машины существенным образом за-

висит от величины коэффициента q и уменьшается с его ростом.

Рассмотрим физический смысл этого коэффициента, приняв для

упрощения преобразований, что

/г

ст

= й

= /г„; = = (7-32)

В этом случае выражение (7.29) может быть записано в виде

где

2йр , 2Й

+ = (7.34)

8/г

6/г,ц

8/г

Преобразуем выражение, стоящее в знаменателе (7.33), следую-

щим образом:

_ 1 2/ят _ 8

8й

яЯ

2 Л

р,/

' 2/ 7Гср

Числитель дроби в полученном выражении представляет маг-

нитное сопротивление ярма

7СТ

^, = 0,5——, (7.36)

знаменатель - магнитное сопротивление воздушного зазора

, • (7.37)

2/ пх р

Коэффициенты 21% представляют отношение среднего значе-

ния магнитного потока к максимальному при гармоническом его

распределении в зазоре и ярме машины. Коэффициент 0,5 учитывает

то обстоятельство, что магнитный поток ярма равен половине потока

полюсного деления. Таким образом, выражение ql а

представляет

отношение магнитных сопротивлений ярма и воздушного зазора:

4 = (7.38)

Ct /?магб

l + q/a ~ = tf

„ >

(7.40)

Ймагй

где коэффициент насыщения магнитной цепи принятой модели

асинхронного двигателя.

В простейшей постановке магнитные свойства ферромагнитных

материалов принимались постоянными. В реальной машине магнит-

ная индукция в ярме статора и ротора на различных участках магни-

топровода принимает различные значения. Вследствие этого магнит-

ная проницаемость материала магнитопровода также имеет различ-

ные величины. Каким образом в условиях одномерной модели можно

учесть это обстоятельство?

При упрощении уравнения (7.9) его первый член заменялся ко-

нечно-разностным выражением. При этом на этапе преобразования

не производилось дифференцирования рассматриваемых выражений

по координате (р. Поэтому, если величина магнитной проницаемости

является функцией тангенциальной координаты, то проводимые пре-

образования не отражаются на конечном результате, так как диффе-

ренцирование рассматриваемых величин производилось по радиаль-

ной координате.

Отличие конечного результата от рассмотренного выше случая

заключается в том, что коэффициент q уже не является постоянной

величиной, а зависит от координаты ф. В этом случае уравнение

(7.23) должно записываться в виде

где коэффициент

Л!-4-<?(Ф)А = -Ц

, (7.41)

До оф

к+ь . \+ъ

1+-

<7(Ф)

= + (7.42)

8/г

(ф) 6/г

(ф)

Для решения уравнения (7.41) с переменными коэффициентами

зависимость

<?(ф)

должна быть задана или определена в ходе итера-

ционного уточнения при решении нелинейной задачи.

Рассмотрим граничные условия краевой задачи при переменной

величине коэффициента q. Если величина этого коэффициента по-

стоянна и не зависит от пространственной координаты ф, то, как

было показано выше, при синусоидальном распределении токовой

нагрузки по длине расточки статора должны выполняться условия

периодичности. В случае переменного коэффициента q постановка

граничных условий должна быть уточнена, исходя из следующих

соображений.

Проинтегрируем радиальную составляющую магнитной индук-

ции в пределах исследуемой области

2п

1 дА

Rol8

\Вкс1<?

= Яо/8 f—=

i о «о Эф

2л

[А(2Л)-А(0)]. (7.43)

Если А(2л) = А(0), ТО рассматриваемый интеграл обращается

в нуль, что эквивалентно условию замкнутости магнитного потока

в исследуемой области. Поскольку это условие должно выполняться

всегда, то оно из граничных условий (7.24) сохраняется и при пере-

менной величине коэффициента q.

Проинтегрируем уравнение векторного потенциала (7.23) по дли-

не окружности:

2я

Хо Эф

•q(q>)A

(7.44)

Правая часть этого выражения всегда равна нулю, поскольку

сумма сторонних токов всегда равна нулю. Следовательно, должно

выполняться граничное условие

'алЛ

Эф

2л

= Хо \qW)AdФ

•

(7.45)

Краевая задача в общем случае должна решаться с учётом полу-

ченного условия, которое, по сути, представляет граничное условие

интегрального типа (см. часть I, подразд. 3.2.3). Условия периодич-

ности, таким образом, будут являться частным случаем условий

(7.45), когда интеграл в правой части этого выражения обращается в

нуль. В большинстве рассматриваемых на практике случаев при

симметричности кривой распределения токовой нагрузки относи-

тельно оси абсцисс указанная симметрия распространяется и на по-