Беляев Е.Ф., Шулаков Н.В., Дискретно-полевые модели электрических машин, учебное пособие

Подождите немного. Документ загружается.

носителю базовой функции, а члены уравнения, соответствующие

точкам за пределами носителя, будут равны нулю.

Примем для упрощения область определения решения краевой

задачи 0<х<Ьодномерной. Разобьём указанную область О<х<L

на конечное число интервалов N и для каждого к-то интервала вве-

дём функцию

ю*(х) =

О, 0

< л: <

(OiW, х

}

<х<х

<й

0)>

<х<х

О, x

<x<x

=1.

(6.12)

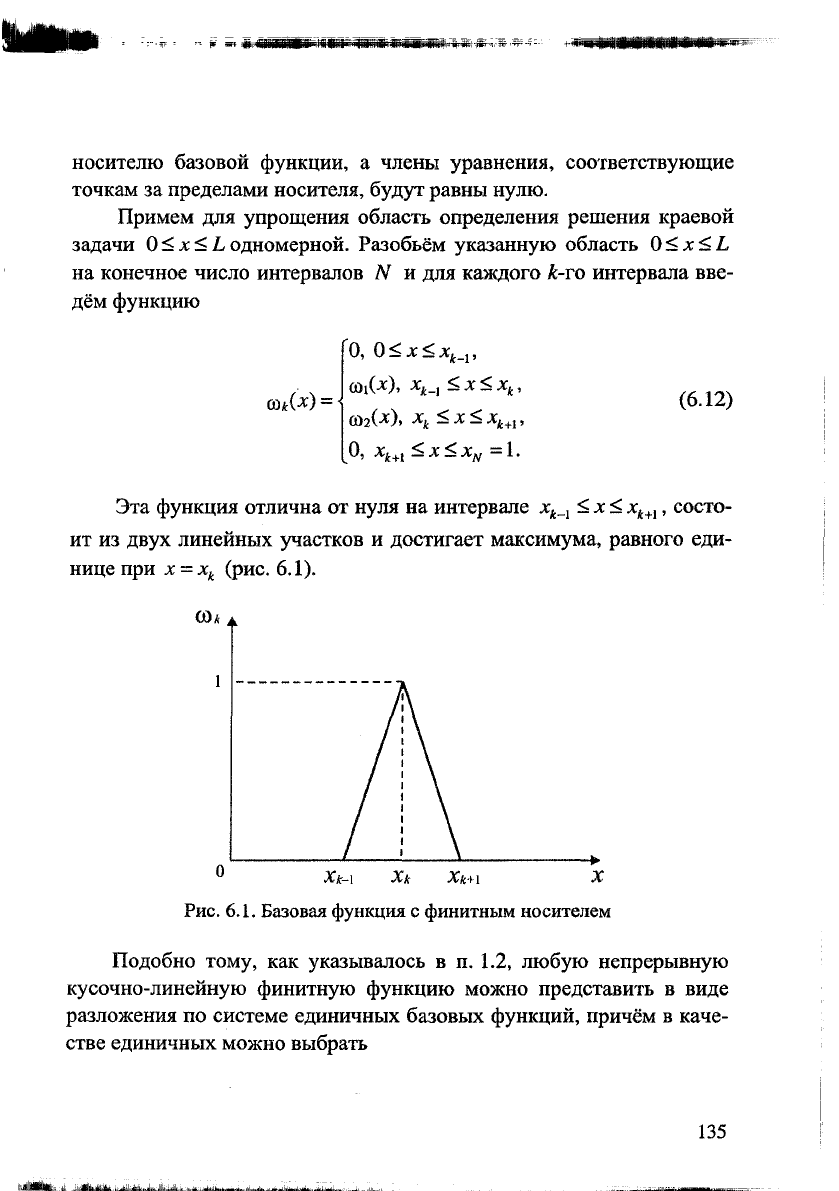
Эта функция отлична от нуля на интервале х

_^ <х<х

, состо-

ит из двух линейных участков и достигает максимума, равного еди-

нице при х = х

(рис. 6.1).

Рис. 6.1. Базовая функция с финитным носителем

Подобно тому, как указывалось в п. 1.2, любую непрерывную

кусочно-линейную финитную функцию можно представить в виде

разложения по системе единичных базовых функций, причём в каче-

стве единичных можно выбрать

«4шаиг««ш «1ММ1М1

фСх) = £ф*ю*С*)>

(6.13)

где коэффициенты <р

равны значениям функции ф(х) в точках х

Рассмотрим свойства базовой функции (6.12), определив её ска-

лярное произведение:

О, п< к-2,

Хк~Хк-\

\m(x)e>N(.x)dx

хш~ Хк-1

Хк+1~ Хк

к -1,

, п

к,

к+1,

(6.14)

О, п>к

Из выражения (6.14) следует, что функция

со

(х) ортогональна

всем функциям

со

(х), кроме <щ

, ш*>a>i+i

•

Поэтому алгебраические

уравнения, описывающие коэффициенты разложения <р

, будут со-

держать всего три члена. Таким образом, использование базовых

функций с финитными носителями позволяет значительно упростить

структуру получаемой системы уравнений и применить для её реше-

ния рассмотренные ранее методы.

6.1. ВАРИАЦИОННО-РАЗНОСТНЫЙ МЕТОД РИТЦА

Методы Ритца, использующие функции с финитными носителями,

принято обозначать как вариационно-разностные методы. Рассмотрим

применение метода Ритца для решения одномерной краевой задачи, за-

писываемой в виде

-A.

p(x)

+ q(x)u = f(x) (6Л5)

ах ах

с однородными граничными условиями и(0) =

и(1) = 0.

Решение краевой задачи соответствует поиску минимума функ-

ционала [33, 34]

Дх) = J

р(х)1^Г +q(x)

-2f(x)u

dx.

(6.16)

Исследуемая область разбивается на N интервалов - конечных

элементов, и решение краевой задачи ищется в виде разложения по

системе базовых функций

14 —I

u(x)

^Ukd>k(x),

(6.17)

k=1

где

mi*) =

Х-Xk~ 1

~ Xk-l

XK+\

, x

<x< х

(6.18)

Хм Xk

О, в остальных точках.

В этом случае минимизируемый функционал может быть пред-

ставлен суммой отдельных составляющих, записанных для каждого

интервала разбиения пространственной координаты:

N-1

T->L

Xk-l

р(х)

+ q(x)

-2f(x)u dx. (6.19)

Запишем уравнение для одной составляющей функционала в точ-

ке x

на интервале jc

< л < jc

i+1

. Искомое решение на этом интервале

содержит три члена и записывается в виде

u(i) -

Ui-i(Oi-i +

urn

+ Wi+iffli+i >

(6.20)

где

(0,-1

(0,

-х

Xi "Xi-l

х -

i+1

— х

~Xi

на интервале jc

<x<x

на интервале х

<х<,

ш,+1

—

на интервале x

<x< х

(6.21)

(6.22)

(6.23)

Интеграл, входящий в выражение (6.19), может быть представлен

в виде суммы двух интегралов для отдельных участков интервала

Xk+i

= J

Хк-1

Хк+1

X/,

(Art

р{х) — +q{x)u

-2f(x)u

\ах

( du^]

р(х) — +q(x)

-2f(x)u

\dx J

dx-

p(x)

+ q(x)

-2f(x)u dx.

da>

Производные — в этих интегралах:

dm-1 -1

Xi-i

d(dj

Xi Xi-l

-1

Xi+i Xi

на интервале <х<х

на интервале х

<х<х

(6.24)

(6.25)

(6.26)

day,

на интервале x, < x < x

i+l

(6.27)

Обозначив первый интеграл (6.24) как

У, (и)

и подставив в него

выражения (6.20), будем иметь:

/,(«)= j

р(х)

Uj-1 ^ Mf

\ Xi Xi-l Af -^(-1

+g(x)

+2f{

A^LJL

l-B±

\Xi Xi-l Xi Xi-\ J

Аналогично второй интеграл (6.24)

Xi X . X

Xi—1

Hi-1 + Ui

\Xi Xi-1 Xi

Xi 1

dx. (6.28)

(и) = |

p(x)

Uj Kj-t-l

+ q(x)

V Xi+l Xi Xi+l Xi J

{

( - \

Xi+l

~X , x-x,

~ Ui+ —Ui+l +

V Xi+l

Xi Xi+l Xi у

+2 /(x)

Xi+l ~~ X ,

~~—Ui H

—Ui+l

V Xi+l Xi Xi+l Xi

dx. (6.29)

Условием минимума функционала является равенство нулю его

производных по искомым величинам, в данном случае

-H/i + /a) = 0.

ам.

(6.30)

Дифференцируя подынтегральное выражение по и, и группируя

подобные члены, запишем уравнение (6.30) в виде

au-iUi-i

ai,iUi

Ui,i+iUi+i —

fit

(6.31)

где

ги-1= f

Xi-1

dx, (6.32)

(li., •

-J

Xi+l

1) (x.-xi-i)

(х

-х>) {x, -*

) _

dx,

Xi+l

ili.i+l —

-x

) (x

-x

)

dx,

(6.34)

Xi+1

f /W

dx+ [/(*)

x -

Xm X

dx.

Xi-1

(6.35)

Рассчитав коэффициенты уравнений а

для

2,..., N -1,

ац-i для i = 2,3,...,

-1, a,,,4i для i

1,2,..., N- 2, правую часть /,

и используя известные граничные условия, получим систему трёх-

членных алгебраических уравнений

Аи

f, (6.36)

где А - матрица с элементами а,/, и - вектор неизвестных; / - век-

тор с рассчитанными компонентами fi.

Решив указанную систему методом прогонки, определим значе-

ния коэффициентов и„ после чего рассчитывается искомое решение

краевой задачи с использованием выражения (6.17).

6.2. ПРОЕКЦИОННЫЙ МЕТОД БУБНОВА-ГАЛЁРКИНА

(МЕТОД ГАЛЁРКИНА)

Рассмотрим решение краевой задачи (6.15) методом Галёркина,

используя вышепринятые положения. Будем считать, что решение

краевой задачи представлено в виде разложения (6.17) с коэффици-

ентами (6.18). В этом случае для отдельного интервала д^ <х<х

решение записывается как (6.20), а коэффициенты разложения для

указанного интервала - по формулам (6.21)—(6.23).

Согласно рассматриваемому методу, умножим уравнение крае-

вой задачи скалярно на

со,

(х) и получим

ах ах

(x)dx

0. (6.37)

Выполним интегрирование первого члена этого выражения по час-

тям и с учётом заданных краевых условий и(0) = 0, и(1) = 0 будем

иметь

d . .du

р(х)—

dx dx

(x)dx

)p(x)—^^-dx. (6.38)

dx dx

Рассматривая краевую задачу на отдельных интервалах, уравне-

ние (6.37) с учётом (6.38) записываем в виде суммы отдельных со-

ставляющих для каждого интервала:

% J

-/W](л)

^dx —

Хч

(6.39)

Выполним интегрирование для отдельных компонентов полу-

ченного выражения:

Хм

Хы

dсо,

, г du

d(O

Т , : du dm,

dx= p(x)

dx+ p(x)

dx dx

dx. (6.40)

Xi-1

ix)

dudcUxl

dx=

* //y /7V J

XI-I

dx dx

•• JpU)

X,-1

XI-

p(x)

dx dx j dx

-1 1

Ui-1

+ Ui

Xi—1

Xi Xi—1 _

/ л

-dx

Uj-Ui-i

(

i ~

i-l f

p(x)dx.

/X,-

» /7r //r J

JCi

(

dCO,

dx dx

PU) м,—r~

M«+i

dx dx

Хм

pU)

-1 1

V Xi+t Xi Xi t! Xi

Г \

cfe:

Xi+1 JCj

(6.42)

Uj+l Uj

(

l-Xif

Хм

j p(x)dx.

du dan , Ui~Ui-

» /7V /7V

J p(je>k—

Hi+1 M,

J . (6.43)

Хн

-Tj+i

.Хм

J ^(х)мШ.Л = J

д(х)иЩ(1х

+ J

д(х)и(0;с1х.

(6.44)

-ы Xt-i Xi

| q(x)m\dx = J q(x)(а

н(йн

,ш,)шДх =

Хм

Xi~i Xi-,

J q(x)

XI~I

Xi X X Xi <

I I I—I

Ui-I

+ Ui

V Xj -Til Xi Xi-l J

x-x.

r (x;-x)(x-xi ,) p

li-i J я(хУ '

+ Ui

1 q(x)

Xi Xi-1

f „

Хм

V Xi Xi-l

dx.

Хм

j д(х)и(й^х

| д(х)(ищ

1+1

со,

)

со

(

Xi+i

= J<?(x)

Xi+i

j q(x)

Хщ-х

V Xi+l Xi

X-X;

Xi+l X

dx-

(6.46)

Xi+l Xi J Xi+l Xi

Xi+l X

Xi+i

V Xi+l Xi

J q(x)

(x,+i-x)(x-x,.)

(xi+l-x,)

dx.

Xi+i

(x,-x)(x-Xi-i)^

| ^(х)мсо,йк =

(

._,

| #(x) — ——-j-^^dx +

(x,-xi-i)

Xi_,

• и

i J q{x)

Xi_,

X ~Xj-l

V Xi

Xi-l

Хм

Xi-i

X,+,

+ u

| q{x)

( _

Xi+l X

dx+ (6.47)

V Xi+l Xi у

+И

i+l

(x-x,.)(x,

-x)

(Xi+1-Xi)

dx.

Xi+i Xi Xi+i

J /(х)со

;

.Л= J Дх) •

"'dx+ J

f(x)

Xi+I

dx. (6.48)

Xi-1

Хм

Xi Xi-1

Xi+l Xi

Подставляя полученные для отдельных интегралов выражения

(6.43), (6.47) и (6.48) в уравнение (6.39), группируя коэффициенты

при неизвестных

1И-ьиьи-,+\,

получим уравнение (6.31) с такими же

коэффициентами.

Этот вывод не является случайным. В работах по численным мето-

дам математики [34] показано, что методы Ритца и Галёркина с использо-

ванием финитных носителей приводят к одинаковым уравнениям в слу-

чае самосопряжённых операторов. Однако метод Галёркина имеет более

широкую область применения, так как может применяться для решения

как самосопряжённых, так и несамосопряжённых краевых задач.

Определение коэффициентов алгебраических уравнений связано

с вычислением определённых интегралов. При известных функциях

р(х), q(x), f(x) эти интегралы могут быть вычислены приближён-

ными методами с помощью квадратурных формул. Если функции

отличаются гладкостью, то при вычислении интегралов их можно

заменить средним на интервале значением, после чего вычисление

интегралов трудностей не вызывает. Например:

х,

J p(x)dx^p

(xi-xi-

Хы

Xi Xi

f{x)(x-x

)flx«f

Xi-\ Xi-i

Xi Xi

{ p(.x)(

-x)(x-Xi-i)dx~ p^j J {xi-x){x-

-i)dx-,

Xi-i Xi-i

Xi Xi

p(x)(x-

fdx~

P,._

0 5

(JC

- x

f dx.

Xi-i Xi-t

6.3. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ

Вариационно-разностные методы (Ритца) и проекционно-

разностные (Бубнова-Галёркина), реализуемые методами вариа-

ционного исчисления, объединены под общим названием «метод

конечных элементов».