Беляев Е.Ф., Шулаков Н.В., Дискретно-полевые модели электрических машин, учебное пособие

Подождите немного. Документ загружается.

Таким образом, для каждого члена разложения к = 1,2,..., N

-1

решается одномерная краевая задача (5.25) с использованием про-

гонки по i при минимальном числе математических операций. Рас-

считав Uк(0

можно по выражению (5.17) восстановить искомую

функцию во всех точках исследуемой области. Нахождение коэффи-

циентов разложения <p

(j) и восстановление искомой функции про-

изводится с использованием БДПФ с минимальной затратой матема-

тических операций. Подобный подход распространяется и на реше-

ние многомерных краевых задач с уравнениями Пуассона, а также

других, более сложных задач, допускающих разделение переменных.

В качестве одномерного в этом случае может быть взят оператор вида

(x)~

ах

г ,ви

кгЮ—

ах

+ R(x

)^—q(x

)U, (5.27)

ах,

т.е. оператор, коэффициенты которого зависят лишь от одной про-

странственной переменной. Полученная краевая задача с указанньм

оператором также решается методом прогонки.

Решение уравнений Лапласа и Пуассона методом разделения

переменных с использованием БДПФ является самым быстрым

и точным способом решения этих уравнений.

Уравнения Лапласа и Пуассона могут быть решены с использова-

нием метода редукции. Идея метода заключается в том, чтобы посте-

пенно понижать порядок системы, исключая последовательно сначала

неизвестные с нечётными номерами, затем неизвестные с номерами,

кратными двум, затем - кратными четырём, восьми и т.д.

Если число неизвестных кратно 2

, то в результате последова-

тельного исключения остаётся одно уравнение, из которого можно

найти неизвестное с номером к 12. После этого осуществляется об-

ратный ход, в результате которого вычисляются значения неизвест-

ных с номерами к/4, к/8, к/16,..,,к/2к, к/к.

Метод редукции по числу вычислительных операций сравним

с методом разделения переменных, т.е. N log

N, однако имеет бо-

лее сложный алгоритм реализации. Описание этого метода и его

использование для решения краевых задач можно найти в работах

[27, 32, 33].

Рассмотрим использование метода разделения переменных

для решения двумерной краевой задачи из предыдущего раздела

(см. пример 4.1).

Пример 5.1. Решение двумерной краевой задачи методом раз-

деления переменных. Решим уравнение Пуассона

£/ Э

£/

ох ду

в квадрате [0:1,0:1] при нулевых граничных условиях:

у)

(I, У) =

U(x, 0)

U(x,

1) =

Задачу решаем в следующей последовательности.

Разбиваем стороны квадрата на N интервалов величиной

hx~hy- —

•

Записываем решение задачи и правую часть дифференциального

уравнения в виде разложения по собственным функциям дискретно-

го оператора Лапласа:

U(i,j)=—Znoxa); f(i,j)

—

N 2

k=1

N 2

k=1

Подставляя указанные разложения в дифференциальное уравне-

ние, будем иметь

JVJ-L N

- 1 N

-1

Z М./')д,[г

*(*')] +

X Г*(|')д

[М0]

"X %(i)MJ).

*=1 k=1 k=l

Л'2-L

где <p

J^fdj^tij),

HHHH

'' * ® m

Д1

и Д

- дискретные двумерные операторы Лапласа.

Учитывая, что

biptU)]=-U\i

U)>

получим

-1

L •-X„Y

(i)

Ф(0}

о.

*=i

С учётом ортогональности собственных функций уравнения для

членов разложения записываются в виде

- XkY »(0 = -Ф

(0,

i-\, 2,...,N

-1; к

1,2,..., N

—1, 7,(0) = 0; Y

(Nd

Заменяя в уравнениях оператор Лапласа конечно-разностным

выражением, получим для каждого уравнения систему трёхчленных

алгебраических уравнений:

Y -2 Y +Y

Пх

/ = 1,2,...,

A?,

-1; к

1,2,..., N

-1; y

ti0

= 0;

Собственные значения дискретного оператора Лапласа известны:

^ кл

А.*

- ^—ГТ sin

• (л,)

Преобразовывая каждое из уравнений системы для

к = 1,2,..., iV

-1, приведём его к виду

AtYi-1

- С,У, + В,Ум = -F,, i

1,2,...,

TV,

-1.

Полученную систему совместно с нулевыми граничными ус-

ловиями решаем методом прогонки с минимальной затратой ма-

тематических операций. Подобные решения осуществляем для

всех к = 1,2,..., N

-1 членов разложения. Восстанавливаем иско-

мую функцию, используя приведённое выше выражение.

- illtlllinWm-niiir Ainium it ™ni'- *****

Результаты решения при = N

= 16,

/ (1:

ЛГ,; 1:

) = 0;

/(7:9,7:9) = 100 представлены ниже.

Программа решения краевой задачи методом разделения пере-

менных:

nl=17; n2=17; hx=l./(nl-l); hy=l./(n2-l); f(l:nl,l:n2)=0.; f(8:10,8:10)=100;

for k=2:n2-l

r 1 =(k-1) *pi/(2. * (n2-1)); r2=sin(rl); Iam(k-l)=4.*r2*r2/(hy*hy);

end

fi(l:nl,l:n2)=0.;

for i=8:10

for k=2:n2

fi(i,k-1)=0;

for j=2:n2

rl=(k-l)*pi*(j-l)/(n2-l); r2=sin(rl); r3=f(ij); fi(i,k-l)=fi(i,k-l)+r2*r3;

. end

end

for k=2:n2-l

for i=l:nl

a(i)=l.; b(i)=l.; c(i)=2.+hx*hx*lam(k-l); ff(i)=hx*hx*fi(i,k-l);

end

alf(2)=0.; bet(2)=0.;

for i=2:nl

r=c(i)-alf(i)*a(i); alf(i+l)=b(i)/r; bet(i+l)=(ff(i)+bet(i)*a(i))/r;

end

y(nl,k-l)=0;

for i=nl-l:-l:l

y(i,k-1 )=alf(i+1 )*y(i+1 ,k- l)+bet(i+1);

end

for i=2:nl-l

for

j=2:n2-1

r4=0;

fork=2:n2-l

rl=(k-l)*pi*(j-l)/(n2-l); r2=sin(rl); r3=y(i,k-l); r4=r4+r2*r3; u(ij-l)=2 *r4/(n2-l);

end

disp(u); surf(u)

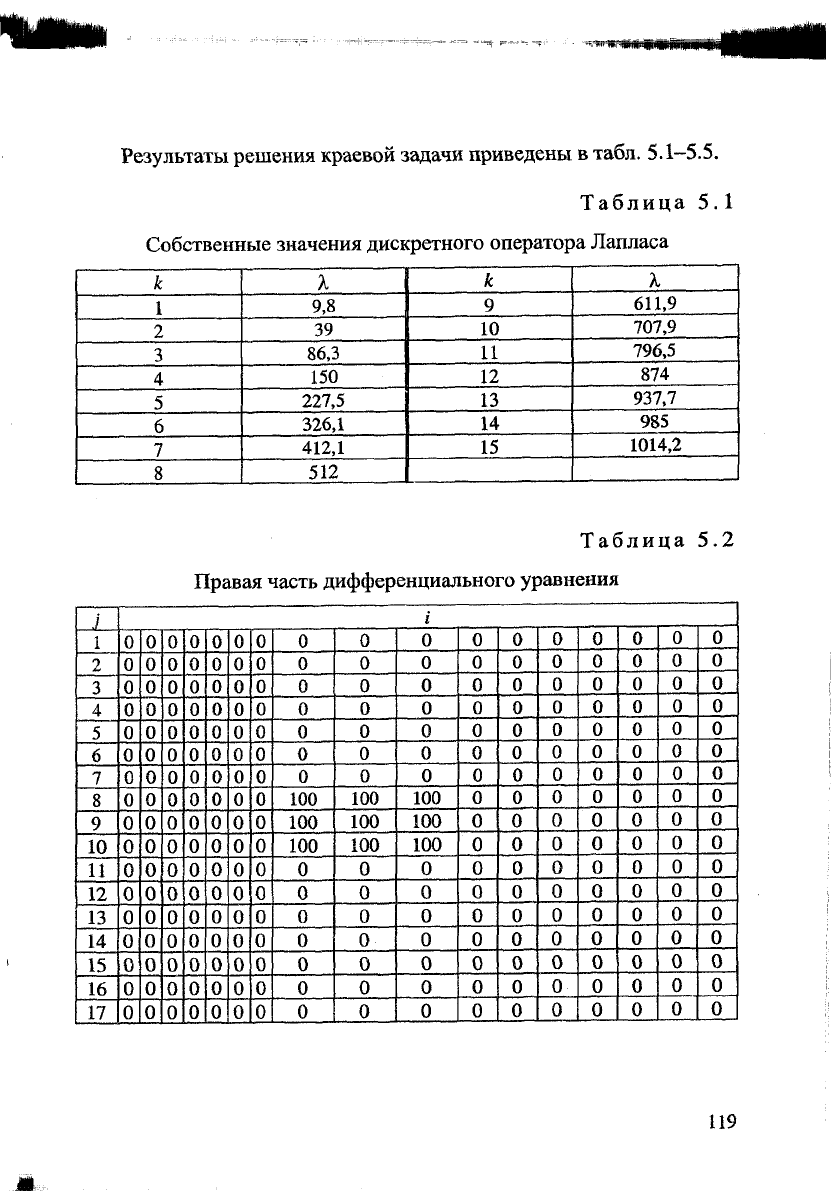
Результаты решения краевой задачи приведены в табл. 5.1-5.5.

Таблица 5.1

Собственные значения дискретного оператора Лапласа

9,8 9

611,9

101,9

86,3

796,5

150 12

874

227,5 13

937,7

326,1

985

412,1 15

1014,2

512

Таблица 5.2

Правая часть дифференциального уравнения

0 0 0 0 0 0

0 0

0 0 0

0 0

4 0

0 0 0

0 0

0 0 0

0 0

0 0 0

0 0

6 0

0 0 0

0 0 0 0

0 0

0 0 0

0 0 0 0

0 0

0 0 0 0

0 0 0 100

100

0 0

9 0

0 0 0 0 0

100

0 0

0 0 0 0

0 0

100

100 0

0 0

11 0

0 0 0

0 0 0 0

0 0

12 0

0 0

13 0

0 0

14 0

0 0

0 0 0 0

0 0

16 0

0 0 0

0 0

0 0 0

0 0 0 0

0 0

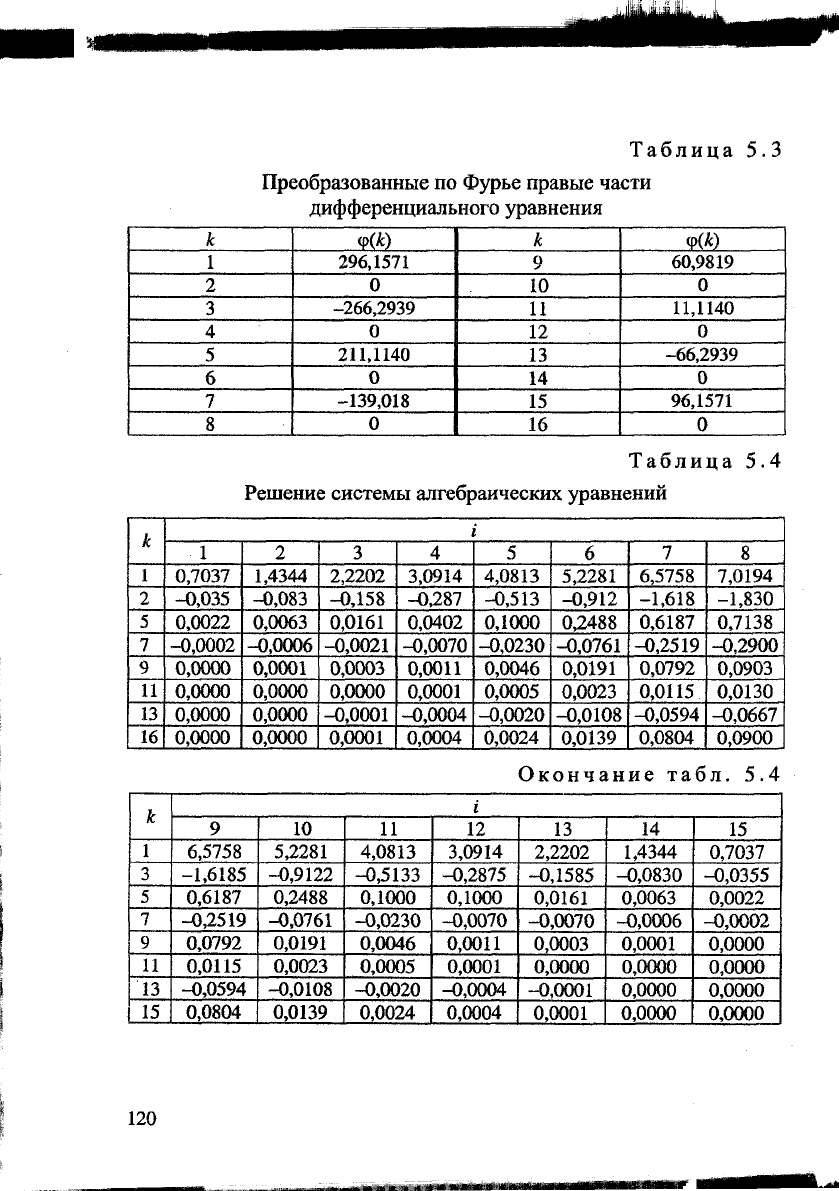
Преобразованные

по

Фурье правые части

дифференциального уравнения

<**)

296,1571

60,9819

-266,2939

11,1140

211,1140

-66,2939

-139,018

96,1571

16 0

Таблица

5.4

Решение системы алгебраических уравнений

1 2 3 4 5

0,7037 1,4344 2,2202 3,0914

4,0813 5,2281

6,5758

7,0194

-0,035 -0,083 -0,158

-0,287

-0,513 -0,912 -1,618 -1,830

0,0022 0,0063 0,0161 0,0402

0,1000 0,2488

0,6187 0,7138

-0,0002

-0,0006 -0,0021 -0,0070 -0,0230 -0,0761 -0,2519 -0,2900

0,0000 0,0001 0,0003

0,0011 0,0046 0,0191

0,0792 0,0903

0,0000

0,0000 0,0000 0,0001 0,0005 0,0023 0,0115 0,0130

0,0000 0,0000 -0,0001 -0,0004

-0,0020 -0,0108

-0,0594

-0,0667

0,0000 0,0000

0,0001

0,0004

0,0024

0,0139 0,0804 0,0900

Окончание табл.

5.4

9 10

11 12 13

6,5758 5,2281

4,0813

3,0914

2,2202 1,4344 0,7037

-1,6185 -0,9122

-0,5133

-0,2875

-0,1585

-0,0830 -0,0355

0,6187 0,2488 0,1000 0,1000 0,0161 0,0063 0,0022

-0,2519 -0,0761

-0,0230 -0,0070

-0,0070

-0,0006 -0,0002

0,0792

0,0191

0,0046 0,0011

0,0003

0,0001 0,0000

0,0115 0,0023

0,0005 0,0001

0,0000

0,0000 0,0000

-0,0594 -0,0108

-0,0020

-0,0004

-0,0001 0,0000 0,0000

0,0804

0,0139 0,0024 0,0004

0,0001

0,0000 0,0000

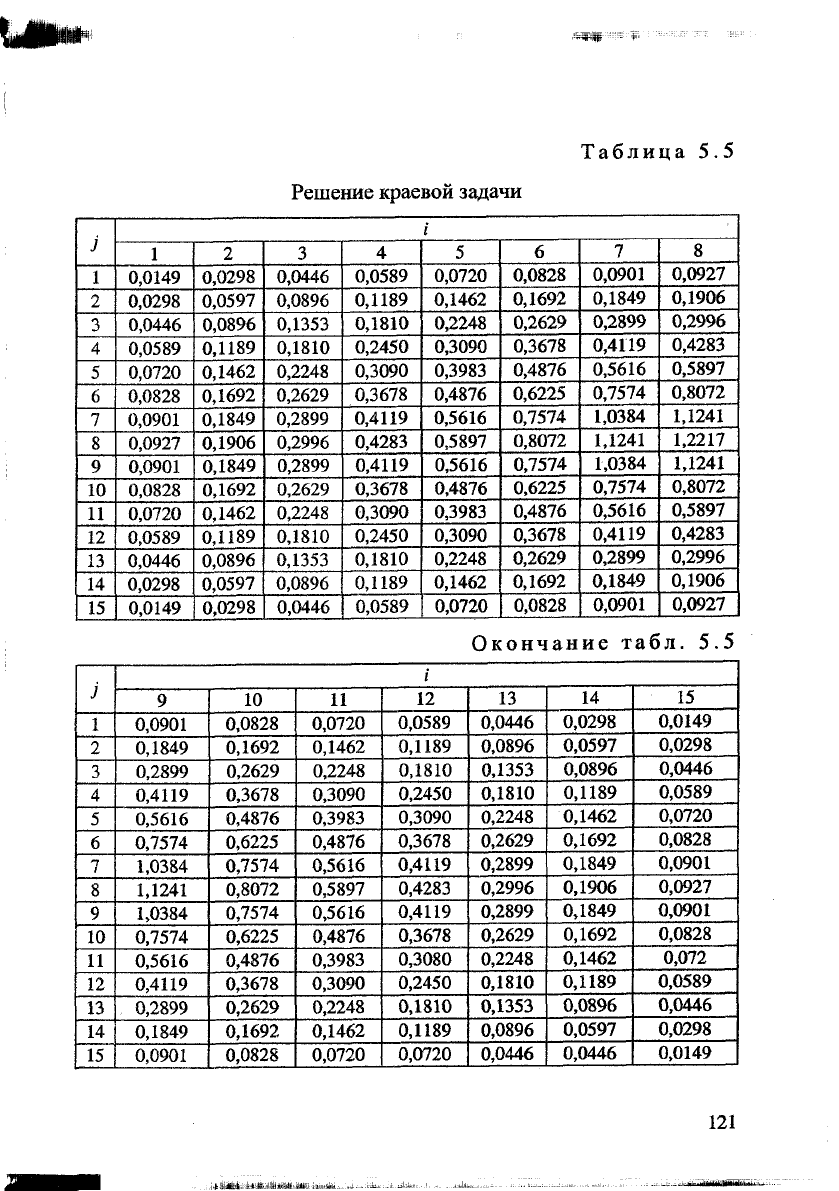
Решение краевой задачи

2 3

4 5

0,0149

0,0298

0,0446

0,0589 0,0720

0,0828

0,0901 0,0927

0,0298

0,0597 0,0896

0,1189 0,1462

0,1692

0,1849 0,1906

0,0446

0,0896

0,1353

0,1810 0,2248

0,2629

0,2899

0,2996

0,0589

0,1189

0,1810

0,2450 0,3090

0,3678

0,4119 0,4283

0,0720

0,1462 0,2248

0,3090 0,3983

0,4876

0,5616

0,5897

0,0828

0,1692 0,2629

0,3678 0,4876

0,6225

0,7574

0,8072

0,0901

0,1849

0,2899

0,4119 0,5616

0,7574

1,0384

1,1241

0,0927

0,1906 0,2996

0,4283 0,5897

0,8072

1,1241 1,2217

0,0901

0,1849 0,2899

0,4119 0,5616

0,7574

1,0384 1,1241

0,0828

0,1692 0,2629

0,3678 0,4876

0,6225

0,7574 0,8072

0,0720

0,1462 0,2248

0,3090 0,3983

0,4876

0,5616 0,5897

0,0589

0,1189 0,1810

0,2450 0,3090

0,3678

0,4119 0,4283

0,0446

0,0896 0,1353

0,1810 0,2248

0,2629

0,2899 0,2996

0,0298

0,0597 0,0896

0,1189

0,1462

0,1692

0,1849 0,1906

0,0149

0,0298

0,0446

0,0589 0,0720

0,0828

0,0901

0,0927

Окончание табл.

5.5

12 13

0,0901

0,0828

0,0720

0,0589

0,0446

0,0298

0,0149

0,1849

0,1692

0,1462

0,1189 0,0896

0,0597

0,0298

0,2899

0,2629

0,2248

0,1810

0,1353

0,0896

0,0446

0,4119

0,3678

0,3090

0,2450

0,1810

0,1189

0,0589

0,5616

0,4876

0,3983

0,3090 0,2248

0,1462

0,0720

0,7574

0,6225

0,4876

0,3678

0,2629

0,1692

0,0828

1,0384

0,7574

0,5616 0,4119

0,2899

0,1849

0,0901

1,1241

0,8072 0,5897

0,4283

0,2996

0,1906

0,0927

1,0384

0,7574

0,5616 0,4119

0,2899

0,1849

0,0901

0,7574

0,6225

0,4876

0,3678

0,2629

0,1692

0,0828

0,5616

0,4876

0,3983

0,3080 0,2248

0,1462

0,072

0,4119

0,3678

0,3090

0,2450

J),1810

0,1189

0,0589

0,2899

0,2629

0,2248

0,1810

0,1353

0,0896

0,0446

0,1849

0,1692

0,1462 0,1189

0,0896

0,0597

0,0298

0,0901

0,0828

0,0720

0,0446

0,0149

О о

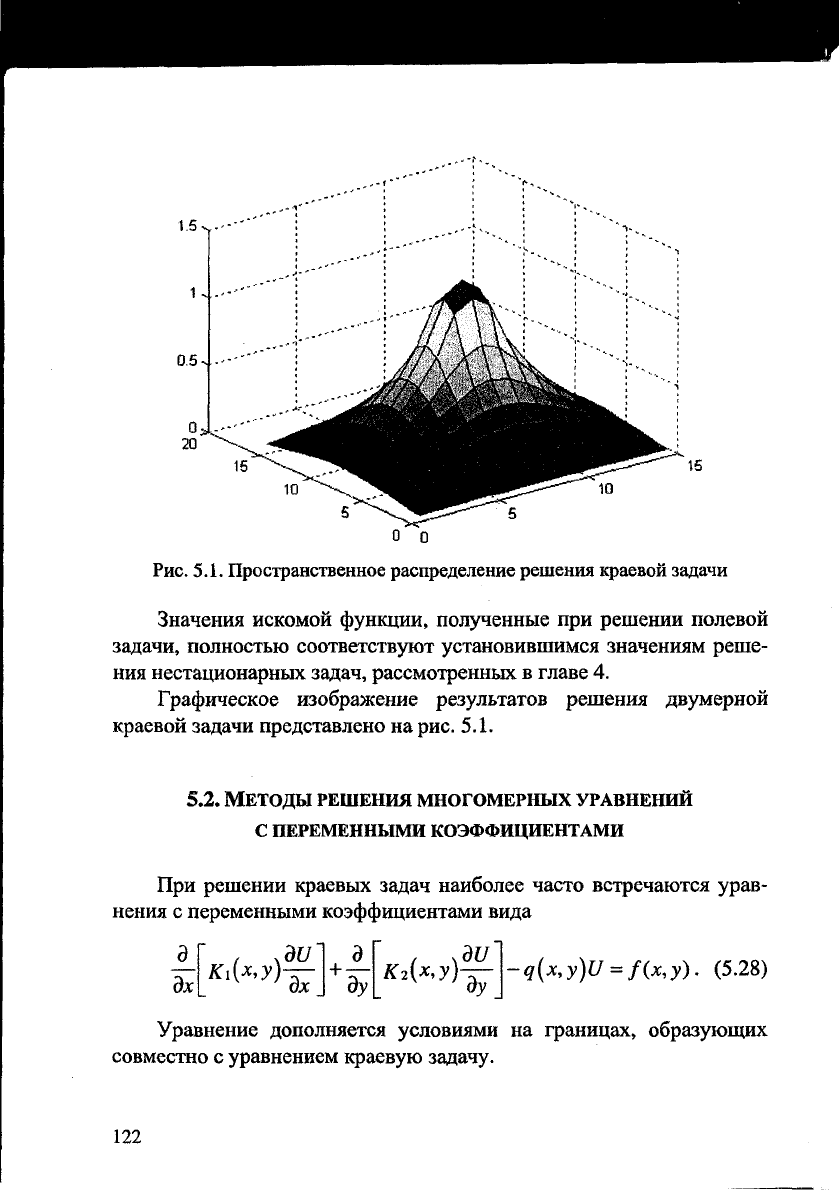
Рис. 5.1. Пространственное распределение решения краевой задачи

Значения искомой функции, полученные при решении полевой

задачи, полностью соответствуют установившимся значениям реше-

ния нестационарных задач, рассмотренных в главе 4.

Графическое изображение результатов решения двумерной

краевой задачи представлено на рис. 5.1.

5.2. МЕТОДЫ РЕШЕНИЯ МНОГОМЕРНЫХ УРАВНЕНИЙ

С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ

При решении краевых задач наиболее часто встречаются урав-

нения с переменными коэффициентами вида

д_

дх

Ki{x,y)

ди_

дх ду

Кг{х,у)

ди_

ду

-q(x,y)U=f(x,y). (5.28)

Уравнение дополняется условиями на границах, образующих

совместно с уравнением краевую задачу.

Указанное уравнение может быть решено конечно-разностными

методами. Для этого дифференциальные операторы заменяются ко-

нечно-разностными выражениями в виде

U M,j U и Uij-Ui-ij

1+0,5, у I Л

/-0,5,/

„ Ui

J+i

-U,j „ Ui.j-Uij-1

i,/+0.5 Л i,j-0,5

(5.29)

-<li,iUi,i =

fi,r

где

oxj

K(x

0,5h

,y)-,

Ki-o,5j

- К (x-

0,5h

у);

iJ+

0,5

= К(*, у + 0,5h

);

-o,5 =

K(x,y- 0,5h

Преобразовывая полученные выражения при естественной ну-

мерации неизвестных, приходим к системе пятичленных алгебраиче-

ских уравнений, записываемых в виде

AijU i-u

BijU

i,j +

CijU ij-i

Di.jUij*

- EijU ij

Fij,

\,2,~.,Nx\ j

1,2,..., Иг- (5.30)

Особенностью этой системы является следующее. Во-первых,

большая размерность системы: число её неизвестных равно N

, где

р- число координат исследуемой области. В частности, для рас-

сматриваемого уравнения (5.28) число неизвестных равно N\

•

Во-вторых, матрица системы оказывается слабо заполненной. В ка-

ждой строке матрицы отлично от нуля лишь незначительное число

элементов: при решении плоскопараллельной задачи число отличных

от нуля элементов равно пяти, а для объёмных задач - семи. Матрица

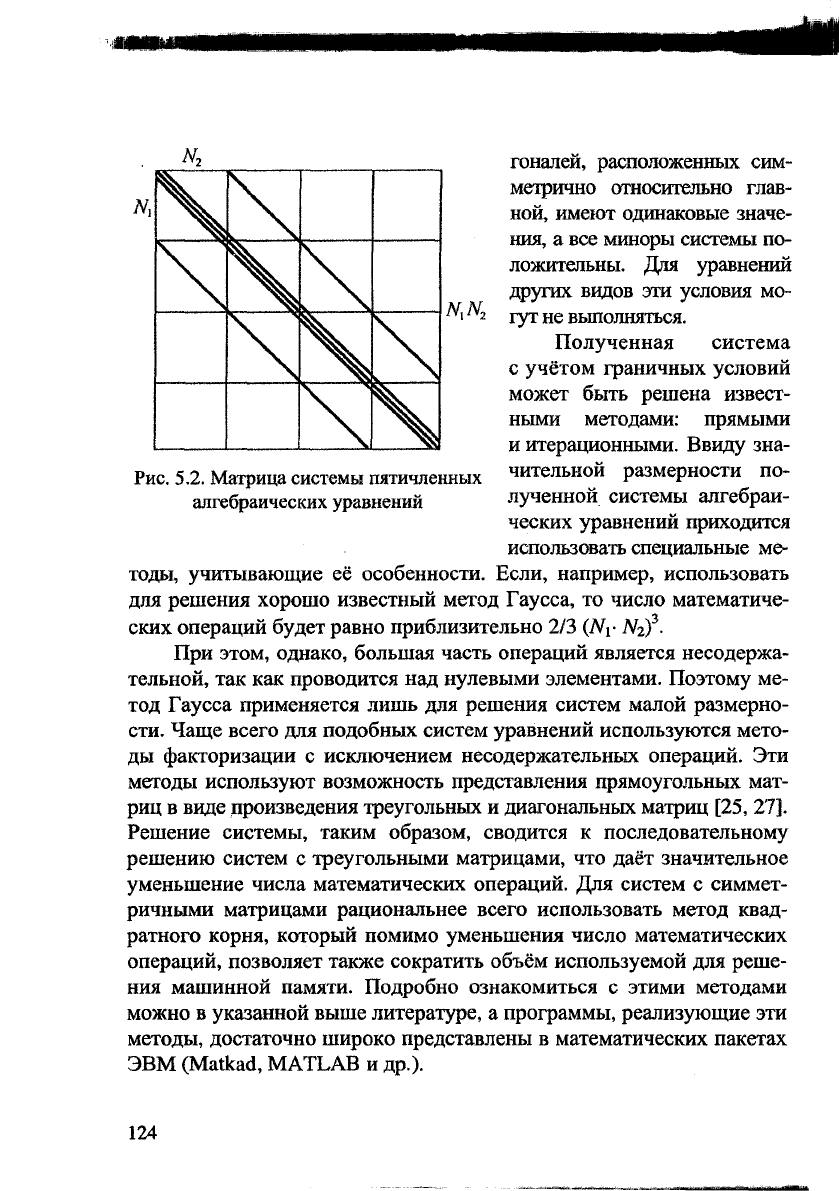
системы имеет ограниченное число диагоналей с ненулевыми эле-

ментами (рис. 5.2). Для уравнений второго порядка с постоянными

и переменными коэффициентами (5.28) матрица является симмет-

ричной и положительно определённой. В этом случае элементы диа-

гоналей, расположенных сим-

метрично относительно глав-

ной, имеют одинаковые значе-

ния, а все миноры системы по-

ложительны. Для уравнений

других видов эти условия мо-

гут не выполняться.

Полученная система

с учётом граничных условий

может быть решена извест-

ными методами: прямыми

и итерационными. Ввиду зна-

чительной размерности по-

лученной системы алгебраи-

ческих уравнений приходится

использовать специальные ме-

Если, например, использовать

для решения хорошо известный метод Гаусса, то число математиче-

ских операций будет равно приблизительно 2/3 (ЛГ

Л^)

При этом, однако, большая часть операций является несодержа-

тельной, так как проводится над нулевыми элементами. Поэтому ме-

тод Гаусса применяется лишь для решения систем малой размерно-

сти. Чаще всего для подобных систем уравнений используются мето-

ды факторизации с исключением несодержательных операций. Эти

методы используют возможность представления прямоугольных мат-

риц в виде произведения треугольных и диагональных матриц [25, 27].

Решение системы, таким образом, сводится к последовательному

решению систем с треугольными матрицами, что даёт значительное

уменьшение числа математических операций. Для систем с симмет-

ричными матрицами рациональнее всего использовать метод квад-

ратного корня, который помимо уменьшения число математических

операций, позволяет также сократить объём используемой для реше-

ния машинной памяти. Подробно ознакомиться с этими методами

можно в указанной выше литературе, а программы, реализующие эти

методы, достаточно широко представлены в математических пакетах

ЭВМ (Matkad, MATLAB и др.).

Рис. 5.2. Матрица системы пятичленных

алгебраических уравнений

тоды, учитывающие её особенности.