Беляев Е.Ф., Шулаков Н.В., Дискретно-полевые модели электрических машин, учебное пособие

Подождите немного. Документ загружается.

2. Чисто индуктивный характер нагрузки. При индуктивном

характере нагрузки ток якоря определяется величиной ЭДС и индук-

тивностью нагрузки:

^, (12.27)

или в комплексном виде

=je>

. (12.28)

Как было показано выше, ЭДС обмотки статора пропорцио-

нальна напряжённости электрического поля. В этом случае плот-

ность тока якоря оказывается пропорциональной векторному потен-

циалу:

^-K

A, (12.29)

где - коэффициент пропорциональности.

Уравнение магнитного поля для этого случая записывается в

виде

1 д

Rl Эф'

-Я

= -М*.м + (12.30)

Аналитическое решение этого уравнения в случае бегущей вол-

ны имеет вид

Но/ в.м Ич)«/ в.м Нчь/ в.м V-oJ В.М "

+ \i

ЛГ

+ е) а

АГ

1 +

Веюгорный потенциал магнитного поля, как и в предыдущем

случае, имеет две составляющие. Первая составляющая определяет

магнитное поле в режиме холостого хода, вторая составляющая -

магнитное поле якоря. В данном случае реакция якоря имеет про-

дольный и размагничивающий характер, т.е. поле якоря ослабляет

поле, создаваемое обмоткой возбуждения. Характер распределения

магнитного поля по длине расточки якоря, полученный при решении

уравнения (12.15), представлен на рис. 12.6. Как и в предыдущем

случае, кривая 1 показывает распределение векторного потенциала

в режиме холостого хода, кривая 2 - распределение векторного по-

тенциала при протекании тока по обмотке якоря при чисто индук-

тивной нагрузке. Поле якоря имеет направление, противоположное

основному магнитному полю, т.е. ослабляет его.

Рис. 12.6. Распределение векторного потенциала СНЯГ

вдоль расточки статора при индуктивной нагрузке

(1 - основное магнитное поле; 2 - поле якоря)

3. Чисто ёмкостный характер нагрузки. В этом случае ток

якоря и его ЭДС связаны следующим соотношением:

e„=^\i

dt. (12.32)

Отсюда, ток в комплексном виде

=j%<c. (12.33)

ЭДС обмотки статора пропорциональна напряжённости элек-

трического поля. Тогда согласно (12.9)

=C&lK

A. (12.34)

Уравнение магнитного поля для ёмкостной нагрузки записыва-

ется в виде

1 д

К ЭФ

(12.35)

где Кс- коэффициент пропорциональности.

Комплексная амплитуда векторного потенциала для этого слу-

чая определяется выражением

М-о/»

-ц

+ д„

Ир J в.м

в.м , Ро/в.м е

Jlv-

„2,

Ч0-

)

Ч «X 1-е

(12.36)

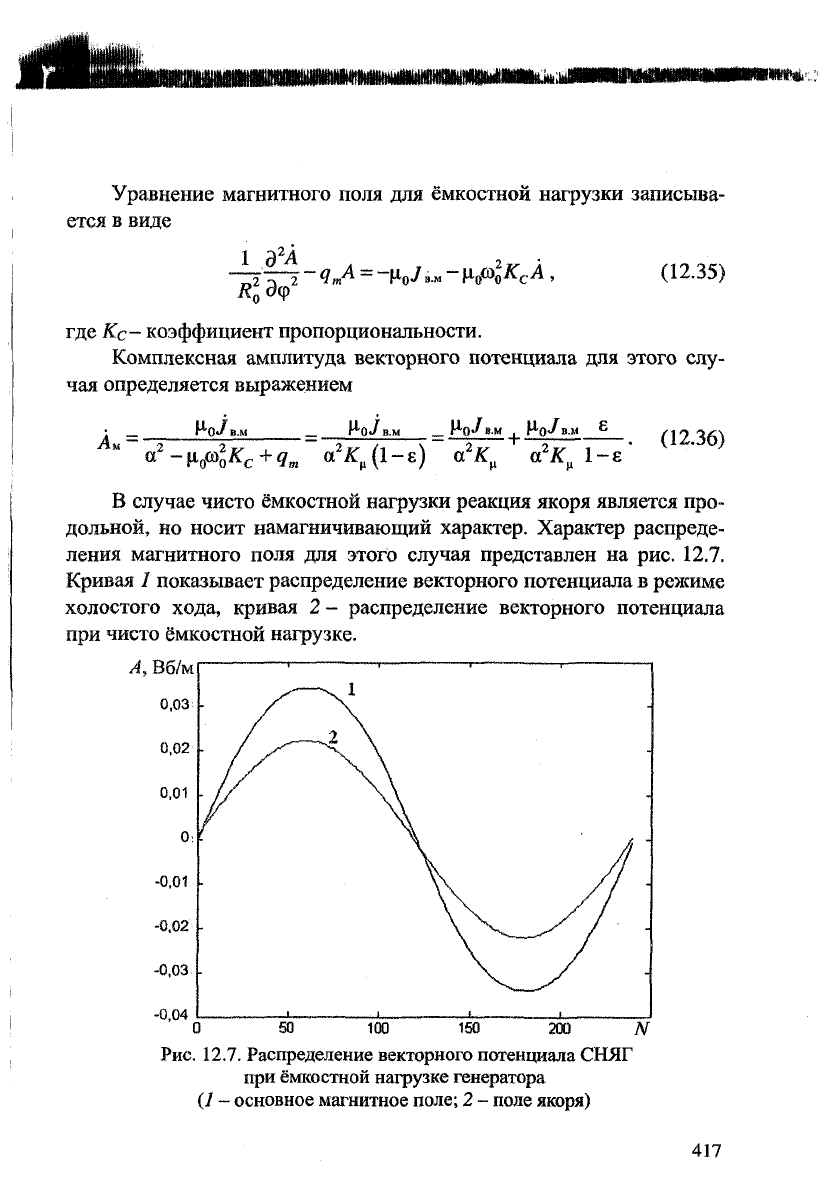
В случае чисто ёмкостной нагрузки реакция якоря является про-

дольной, но носит намагничивающий характер. Характер распреде-

ления магнитного поля для этого случая представлен на рис. 12.7.

Кривая 1 показывает распределение векторного потенциала в режиме

холостого хода, кривая 2 - распределение векторного потенциала

при чисто ёмкостной нагрузке.

А, Вб/м

SO 100 150 200 N

Рис. 12.7. Распределение векторного потенциала СНЯГ

при ёмкостной нагрузке генератора

- основное магнитное поле; 2 - поле якоря)

Рассчитав магнитное поле, можно, используя известные соот-

ношения, определить фазные и линейные ЭДС, а также соответст-

вующие напряжения на выходе генератора.

При произвольном характере нагрузки аналитический расчёт

магнитного поля становится затруднительным. В этом случае расчёт

магнитного поля генератора рационально производить, используя

математическую модель.

В рабочем режиме ЭДС генератора определяется суммарным

магнитным потоком, который зависит и от тока возбуждения и от

тока якоря. В свою очередь ток якоря зависит от напряжения генера-

тора, а также от величины и характера сопротивления нагрузки, ко-

торые обычно известны.

Нагрузочный режим генератора принято описывать внешней

характеристикой - зависимостью выходного напряжения генератора

от тока нагрузки при неизменной величине тока возбуждения и не-

изменном коэффициенте мощности.

Для определения тока якоря воспользуемся принципом суперпо-

зиции. Будем рассматривать поле генератора в виде отдельных со-

ставляющих: основного поля, создаваемого обмоткой возбуждения,

поля якоря, возникающего в машине при протекании тока по обмот-

ке якоря и полей рассеяния якоря, также возникающих при протека-

нии тока по обмотке якоря. Каждое из этих полей наводит в обмотке

якоря свои ЭДС, суммарная величина которых и определяет величи-

ну тока якоря при заданном сопротивлении нагрузки.

ЭДС, наводимую в проводниках каждой фазы якоря основным

потоком, будем рассчитывать, используя известное выражение

ёоф

= -ушотоф> (12.37)

где

Ч'оф

- потокосцепление фазы, создаваемое обмоткой возбуждения.

Аналогичным образом определяется ЭДС самоиндукции, наво-

димая в обмотке якоря магнитным полем якоря.

7шоТяф

(12.38)

где

оф

- потокосцепление, создаваемое токами якорной обмотки.

Потокосцепление обмотки якоря возникает в результате проте-

кания тока по проводникам обмотки якоря. С учётом принципа су-

перпозиции потокосцепление каждой фазы может рассматриваться,

как и для асинхронных машин, в виде суммы потокосцеплений, соз-

даваемых токам отдельных фаз:

¥аА = Ш

+ 11г1в + Ш

'' (12.39)

Т<,й = £

/Л + /

2/В + Ь2З/С; (12.40)

с = Ш

+ 1ъг1в + Ш

- (12.41)

ЭДС, наводимую в обмотке якоря полями рассеяния, будем учи-

тывать соответствующим падением напряжения на сопротивлении

рассеяния якоря.

При симметричной нагрузке генератора, симметрии параметров

обмоток и симметрии магнитной цепи уравнения, записываемые по

второму закону Кирхгофа для отдельных фаз, имеют вид:

ёоА

- МоЧ* = i

(ZG

+ ZA); (12.42)

во в -

JTOOVAB

= ISIZAB + ZB) ; (12.43)

ёос - JMVAC = ICIZAC + ZC), (12.44)

где

ZOA, ZOB,

Zac ~ сопротивления фазных обмоток генератора;

, ZBIZC~ сопротивления нагрузки генератора.

Если фазные обмотки генератора и сопротивления нагрузки со-

единены по схеме «звезда» с нейтральным проводом, то система фаз-

ных токов однозначно определена системой фазных ЭДС.

Для определения величины фазных токов при симметричной на-

грузке используется совместное решение систем уравнений (12.15),

(12.39)-(12.41), (12.42)-(12.44). Потокосцепления фаз определяются

через значения векторных потенциалов в точках расположения про-

водников рассматриваемой фазы:

• V'

' V'T / . • Ч

1 w.

(12.45)

где p - число полюсов генератора; q - число пазов на полюс и фазу;

if, - число витков в катушке обмотки; А н И -Ак - значения вектор-

ного потенциала в точках, координаты которых соответствуют коор-

динатам проводников сторон катушки обмотки.

Система указанных уравнений является определённой и позво-

ляет рассчитать значения фазных токов по известным величинам

фазных ЭДС холостого хода и заданным значениям сопротивлений

нагрузки. Величины фазных ЭДС холостого хода определены значе-

ниями тока возбуждения в режиме холостого хода с использованием

приведённой выше программы.

При соединении нагрузки по схеме «звезда» без нейтрального

провода система фазных токов не может быть однозначно опреде-

ленной. В этом случае используется система уравнений Кирхгофа,

записываемая для двух фаз, и уравнение токов для рассматриваемой

схемы соединения обмоток:

ёлв

-ёв>

ёс.А =

ёс ~ ёл ! I

+ 1

+ /

=0> (12.46)

где ё,иё

,ёс- фазные ЭДС, определяемые суммарным магнитным

потоком обмотки возбуждения и обмоток якоря:

=ё

л-МУаА> {12А1)

; (12.48)

=ё

0С

-]т

Ч>

сС

. (12.49)

Фазные токи в данной схеме определяются при совместном ре-

шении системы (12.15), (12.45)-( 12.49), которая также является оп-

ределённой.

Для решения указанных систем уравнений рационально исполь-

зование описанного ранее метода суперпозиции. Программа реали-

зации указанных задач представлена ниже. Для этого потокосцепле-

ния фаз статора выражаются через его токи по (12.39)-(12.41). Заме-

няя в выражениях фазных ЭДС потокосцепления якоря через его то-

ки, приходим к системе трёх уравнений с тремя неизвестными, кото-

рая решается традиционными методами. Программа расчёта внеш-

них характеристик, реализующая описанную методику, приведена

в примере 12.2.

Пример 12.2. Расчёт внешних характеристик СНЯГ при сим-

метричной нагрузке. Рассчитать внешние характеристики образца

синхронного неявнополюсного генератора, используя параметры ге-

нератора из примера 12.1. Величины фазных ЭДС в режиме холостого

хода принять равными 300 В. Активные сопротивления нагрузки

в рабочем режиме уменьшаются от 5000 до 100 Ом, индуктивные со-

противления составляют 0,5 активных, ёмкостные - 0,4 активных.

Программа расчета внешних характеристик при симметричной

нагрузке:

n=240; r0=45.5e-3; q=0.5*l.e-3; mu0=4.*pi*l.e-7; om=100.*pi; jh=14; nn=l;

wa=8.; la=0.1; hf=2.*pi/n; me=0.+l.i; del=0.5e-3; alf0=2 *pi/n; za=0.+5.i; zb=za;

zc=za; edsa=300.; edsb=300.*exp(-2.*me*pi/3.); edsc=300.*exp(2.*me*pi/3.);

eab=edsa-edsb; eca=edsc-edsa; m=l; mm=l; ia=1.0; ib=0.; ic=0.; a(l:n)=1.0;

b(l:n)=1.0; c(l:n)=2.+rG

2*hf

2*q;

while m<5

ta=ia*wa/(del*r0*hf); tb=ib*wa/(del*r0*hf); tc=ic*wa/(del*r0*hf);

for j=2:6

fa(j)=ta;fa(j+8)=ta;fa(j+16)=ta;fa(j+24)=ta;fa(j+32)=ta; fa(j+40)=-tc;

fa(j+48)=-

tc;

fa(j+56)=-tc;fa(j+64)=-tc;fa(j+72)=-tc;

fa(j+80)=tb; fa(j+88)=tb; fa(j+96)=tb;

fa(j+104)=tb;

fa(j+112)=tb;

end

for j=l:120

fa(j+120)=-fa(j);

end

ft(l:n)=muO*fa(l:n)*rQ

2*hf

alf(2)=b(l)/c(l); bet(2)=ft(l)/c(l)-,

gam(2)=a(l)/c(l);

for j=2:n

rl=c(j)-alf(j)*a(j); alf(j+l)=b(j)/rl;

r2=ft(j)+a(j)*bet(j);

bet(j+l)=r2/rl;

gam(j+l)=gam(j)*a(j)/rl;

end

p(n-l)=bet(n); q(n-l)=alf(n)+gam(n);

for

j=n-2:-l:l

p(j)=alf(j+l)*p(j+l)+bet(j+l); q(j)=alfO+l)*q(j+l)+gamO+l);

end

r3=bet(n+l)+alf(n+l)*p(I); r4=l.-gam(n+l)-alf(n+l)*q(l); y(n)=r3/r4;

for j=l:n-l

y(j)=p(j)+y(n)*q(i);

end

pota=0,; potb=0.; potc=0.; pota 1=0.; potbl=0.; potcl=0.;

pota2=0.; potb2=0.; potc2=0.;

for j=2:6

pota 1 =pota 1+y0)+y(j+8)+y(j

16)+y(j+24)+y(j+32);

pota2=pota2+y(j+120)+y (j+128)+y(j+136)+y(j+144)+y(j+152);

pota=la* wa*(pota 1 -pota2);

potb 1 =potb l+y(j+80)+y(j+88)+y(j+96)+y(j+104)+y(j+112);

potb2=potb2+y(j+200)+y(j+208)+y(j+216)+y(j+224)+y(j+232);

potb=la* wa*(potb 1 -potb2);

potc 1 =potc l+y(j+

160)+y(j+

168)H-y(j+176)+y(j+184)+y(j+192);

potc2=potc2+y(j+40)+y(j+48)+y(j+56)+y(j+64)+y(j+72);

potc=la* wa*(potc 1 -potc2);

end

if m==l

l=pota/ia; 121=potb/ia; 131=potc/ia; ia=0.; ib=l.; ic=0.;

end

if m==2

112=pota/ib; 122=potb/ib; 132=potc/ib; ia=0.; ib=0.; ic=l.;

end

if m==3

113=pota/ic; 123=potb/ic; 133=potc/ic;

L=[l 11,112,113;I21,122,123;131,132,133]

end

if m==4

disp(abs(y));

end

m=m+l;

end

while mm<4

while nnclOQ

if nn==l

rna=l.e8; rnb=l.e8; rnc=l.e8; xna=0.; xnb=0.; xnc=0.;

end

if nn>l

rna=5000.-49.*(nn-l); rnb=rna; rnc=rna;

end

if mm=l

xna=0.; xnb=xna; xnc=xna;

end

if mm==2

xna=0.5 *rna;xnb=xna;xnc=xna;

end

if mm=3

xna=-0.4*rna; xnb=xna;xnc=xna;

end

zna=rna+me*xna; znb=rnb+me*xnb; znc=rnc+me*xnc;

zsa=za+zna; zsb=zb+znb; zsc=zc+znc;

z 11 =zsa+zsb+me*om*(l 11-112-121+122) ;z 12=zsb+me*om*(l 13-112+122-123);

z21=-zsa+me*om*(131-132-111+112) ;z22=zsc+me*om*(133-132+l 12-113);

D=zll*z22-zl2*z21;Dl=eab*z22-eca*zl2; D2=eca*zl l-eab*z21;

ia=Dl/D; ic=D2/D; ib=-ia-ic;ua=ed.sa-me*om*(l

11 *ia+l

12*ib+I13*ic);

ub=edsb- me*om*(121*ia+I22*ib+123*ic);uc=edsc-

me*om*(131*ia+132*ib+133*ic);

disp(abs(ia)) ;disp(abs(ua));

if mm==l

n 1 (nn)=abs(ia); n2(nn)=abs(ua);n3(nn)=0.;

end

if mm==2

n4(nn)=abs(ia); n5(nn)=abs(ua);

end

if mm==3

n6(nn)=abs(ia); n7(nn)=abs(ua);

end

nn=nn+l;

end

mm=mm+1; nn= 1;

end

plot(nl,n2,nl,n3,n4,n5,n6,n7)

Внешняя характеристика генератора - зависимость его напряжения

от тока нагрузки - определяется характером нагрузки (рис. 12.8). При

индуктивной нагрузке характеристика имеет крутопадающий вид,

поскольку поле якоря вызывает уменьшение основного магнитно-

го поля, создаваемого обмоткой возбуждения. При ёмкостной на-

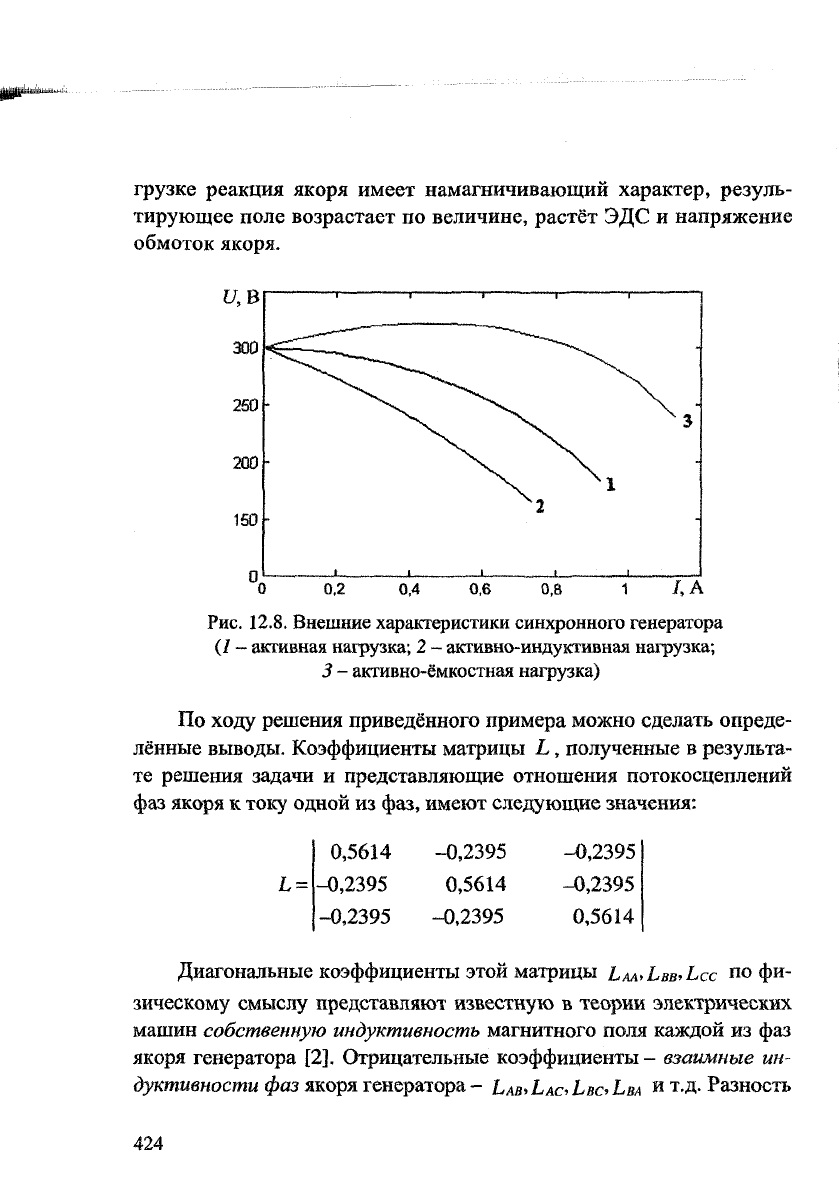
грузке реакция якоря имеет намагничивающий характер, резуль-

тирующее поле возрастает по величине, растёт ЭДС и напряжение

обмоток якоря.

200

300

250

150

/, А 0,2 0,4 0,6 0,8

Рис. 12.8. Внешние характеристики синхронного генератора

(/ - активная нагрузка; 2 - активно-индуктивная нагрузка;

3 - активно-ёмкостная нагрузка)

По ходу решения приведённого примера можно сделать опреде-

лённые выводы. Коэффициенты матрицы L, полученные в результа-

те решения задачи и представляющие отношения потокосцеплений

фаз якоря к току одной из фаз, имеют следующие значения:

Диагональные коэффициенты этой матрицы LM>LBB>LCC по фи-

зическому смыслу представляют известную в теории электрических

машин собственную индуктивность магнитного поля каждой из фаз

якоря генератора [2]. Отрицательные коэффициенты - взаимные ин-

дуктивности фаз якоря генератора -

LAB>LAC->LBC>LBA

И Т.Д. Разность

0,5614 -0,2395 -0,2395

L= -0,2395 0,5614 -0,2395

-0,2395 -0,2395 0,5614