Белов А.В., Коровин Ю.В. Устойчивость электрических систем
Подождите немного. Документ загружается.


31
sin
q
q
E
d
E U
P
x
Σ
⋅
= ⋅ δ
(1.8.4)
sin
E
d
E U
P
x
′
Σ
′
⋅
′
= ⋅ δ
′
(1.8.5)
Г
Г
Г
вн
sin
U
U U
P
x
⋅
= ⋅ δ
(1.8.6)
Индекс в выражении мощности указывает, через какую ЭДС она
выражена. Формула (1.8.4) уже была нами выведена другим способом
(см. п. 1.4). Выражениями (1.8.5) и (1.8.6) удобнее было бы пользо-
ваться, если бы в них вместо углов
′
δ
и
Г
δ
присутствовал бы угол
δ
.
Введя угол
ψ =δ+ϕ
, получим выражение активной мощности
cos cos( ) (cos cos sin sin )
P UI UI UI
= ϕ= ψ−δ = ψ⋅ δ+ ψ⋅ δ
, (1.8.7)
или с учетом соотношений для составляющих:
cos
q
I I
ψ =
;
sin
d
I I
ψ =
;
cos
q
U U
δ =
;
sin
d
U U
δ =
, получим
q q d d
P U I U I
= +
.
Кроме того, из диаграммы видно, что
sin
q
d
U
I
x
Σ
⋅ δ
=
; (1.8.8)
cos
q
d
d
E U
I
x
Σ
′
− ⋅ δ
=
′
; (1.8.9)
Г
вн
cos
d
U U
I
x
− ⋅ δ
=
. (1.8.10)
После подстановки (1.8.9) и (1.8.10) в (1.8.7), получим требуемые
выражения мощности, содержащие только угол
δ
:
2
( ) sin sin(2 )
2
q
q
d d
E
d d d
E U
x x
U
P
x x x
′
Σ Σ Σ
′
⋅
′
−
δ = ⋅ δ− ⋅ ⋅ δ
′ ′
⋅
; (1.8.11)
Г
2
Г
вн вн
( ) sin sin(2 )
2
q
q
d
U
d
U U
x
U
P
x x x
Σ
⋅
δ = ⋅ δ− ⋅ ⋅ δ
⋅
. (1.8.12)
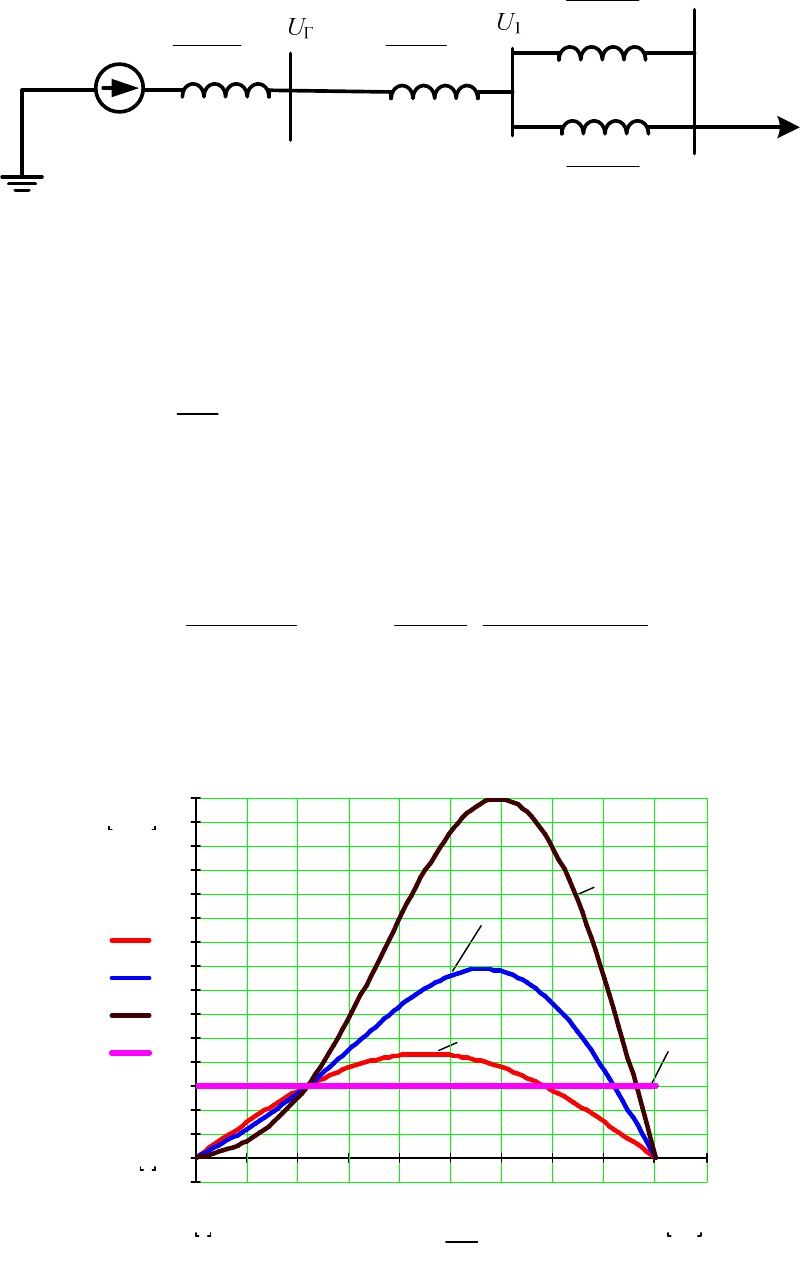
Пример 1.8.1 Построение характеристики мощности простейшей
системы, оснащенной АРВ ПД , а затем АРВ СД.
В качестве примера возьмем систему, описанную в п.1.3. Её уп-
рощенная сема замещения при оснащении АРВ ПД, имеет вид, изо-
32
браженный на рисунке 1.8.3 (т.е. представлена проекцией переходной
ЭДС
E
′
на ось
q
за сопротивлением
d
x
′
).
1,112
d
х
j
′
Т
0,44
х
j
Л1
0,734
х
j
0 0
P Q
+
Л2
0,734
х
j
q
E
′
0,97
U
=
Рисунок 1.8.3 – Схема замещения системы, оснащенной АРВ ПД
Определим переходную ЭДС
E
′
:
23,429
1,37 0,594 1,493
j
d
E U I x j e
°
Σ
′
= + ⋅ = + = ⋅
ɺ ɺ ɺ
,
где
Л1
Т
1,919
2
d d
x
x x x j
Σ
′ ′
= + + =
и
0
23,429
′
δ = °
.
Определим проекцию переходной ЭДС на ось
q
:
0 0
cos( ) 1,493 cos(43,735 23,429 ) 1,4.
q
E E
′ ′ ′
= ⋅ δ −δ = ⋅ °− ° =
Напишем выражение активной мощности по (1.8.11):
2
1,4 0,97 0,97 7,628 1,112
( ) sin sin(2 )
1,919 2 8,435 1,919
q
E
P
′
⋅ −
δ = ⋅ δ− ⋅ ⋅ δ
⋅
;
( ) 0,708 sin 0,189 sin(2 )
q
E
P
′
δ = ⋅ δ− ⋅ δ
.
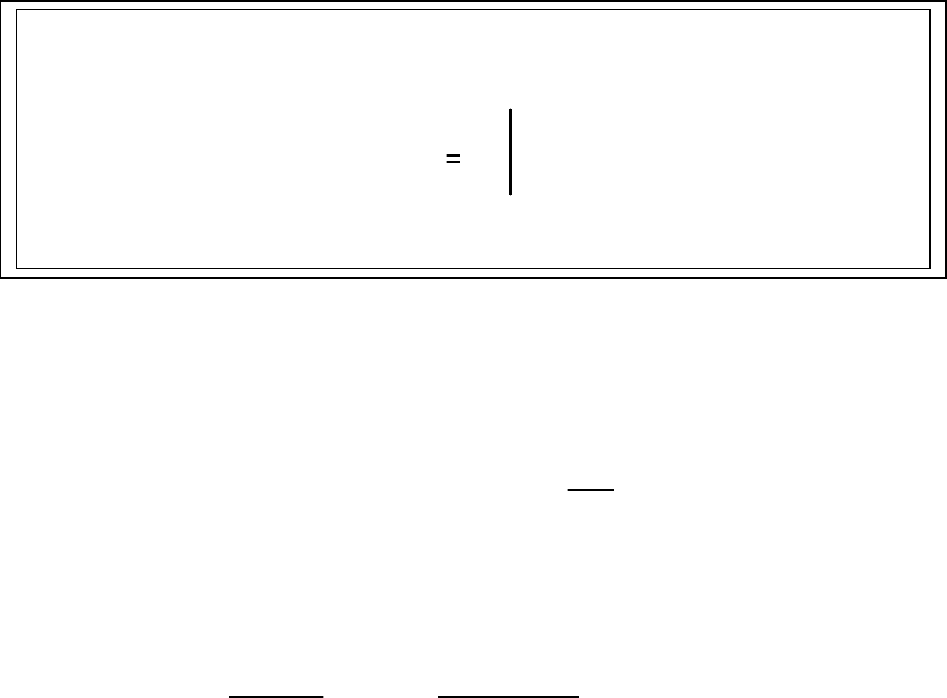
Вид характеристики представлен на рисунке 1.8.4 (средняя кривая)
δ
( )
P
δ
0
P
( )
U
Гq
P
δ
( )
E
q
P
′
δ
( )
E
q
P
δ
0 20 40 60 80 100 120 140 160 180 200
0.1−
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
1.3
1.4
1.5
1.497
0
P δ( )
Pe' δ( )
Pu δ( )
P0
1800
δ
180
π
⋅
33
Рисунок 1.8.4 – Характеристики мощности простейшей системы без АРВ
(нижняя кривая), с АРВ ПД (средняя кривая) и АРВ СД (верхняя кривая)
Необходимо определить максимальное значение мощности. Для
этого в программе Mathcad необходимо в выражении мощности вы-
делить переменную (
δ
), а затем продифференцировать все выраже-
ние. Это можно сделать, выполнив поочередно команды Simbolics –
Variable – Differentiate (Символьная – Переменная – Дифферен-
цирование). Под нашим выражением появится выражение производ-
ной, которое необходимо приравнять нулю (знак равенства должен
быть логическим, из панели инструментов Boolean – Логическая), и
решить относительно переменной
δ
так, как это показано на рисунке
1.8.5.
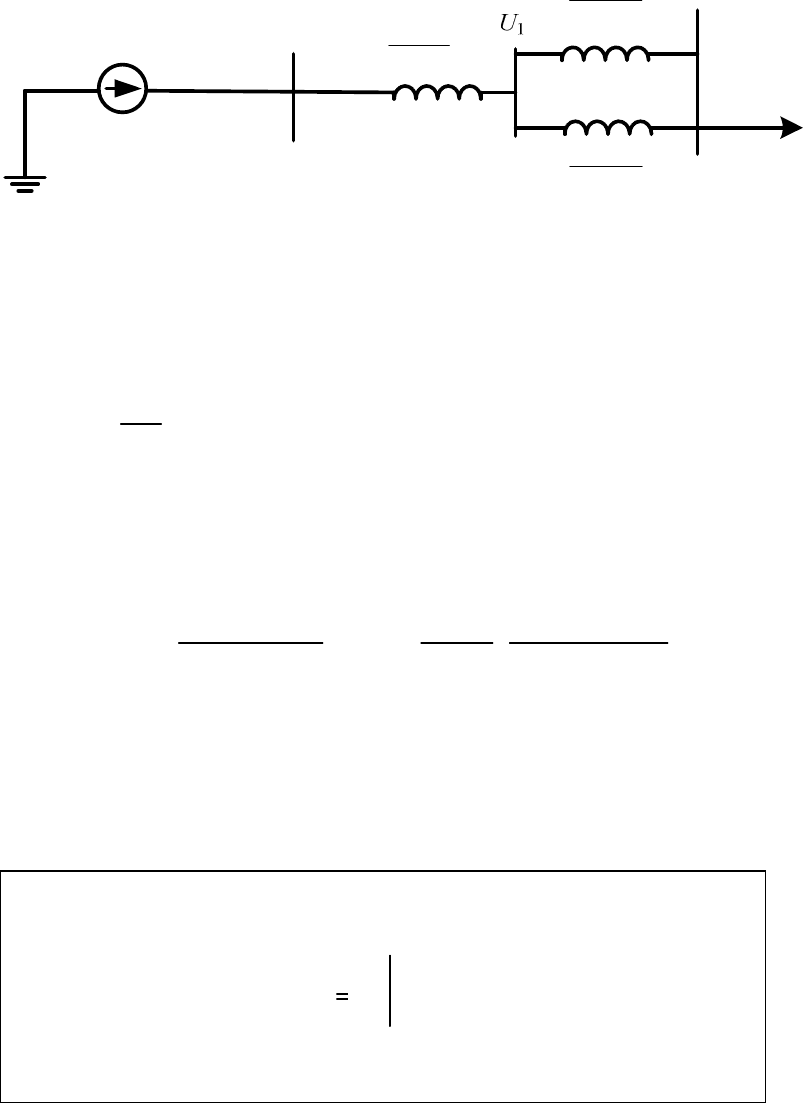
Рисунок 1.8.5 – Часть экрана компьютера с определением производной
выражения мощности и её максимума
Как известно, производная равна нулю в точке экстремума. Из
четырех полученных решений нас устраивает только действительное
положительное значение:
180
1,96
рад 1,96 112,3
δ = = ⋅ = °
π
. Подставляя
это значение в выражение мощности, получим
max
0,708 sin(112,3 ) 0,189 sin(2 112,3 ) 0,788
q
E
P
′
= ⋅ ° − ⋅ ⋅ ° =
.
Коэффициент запаса статической устойчивости равен
0
0
0,788 0,3
100% 100% 163%.
0,3
q
m
E
P P
K
P
′
−
−
⋅ = ⋅ =
=
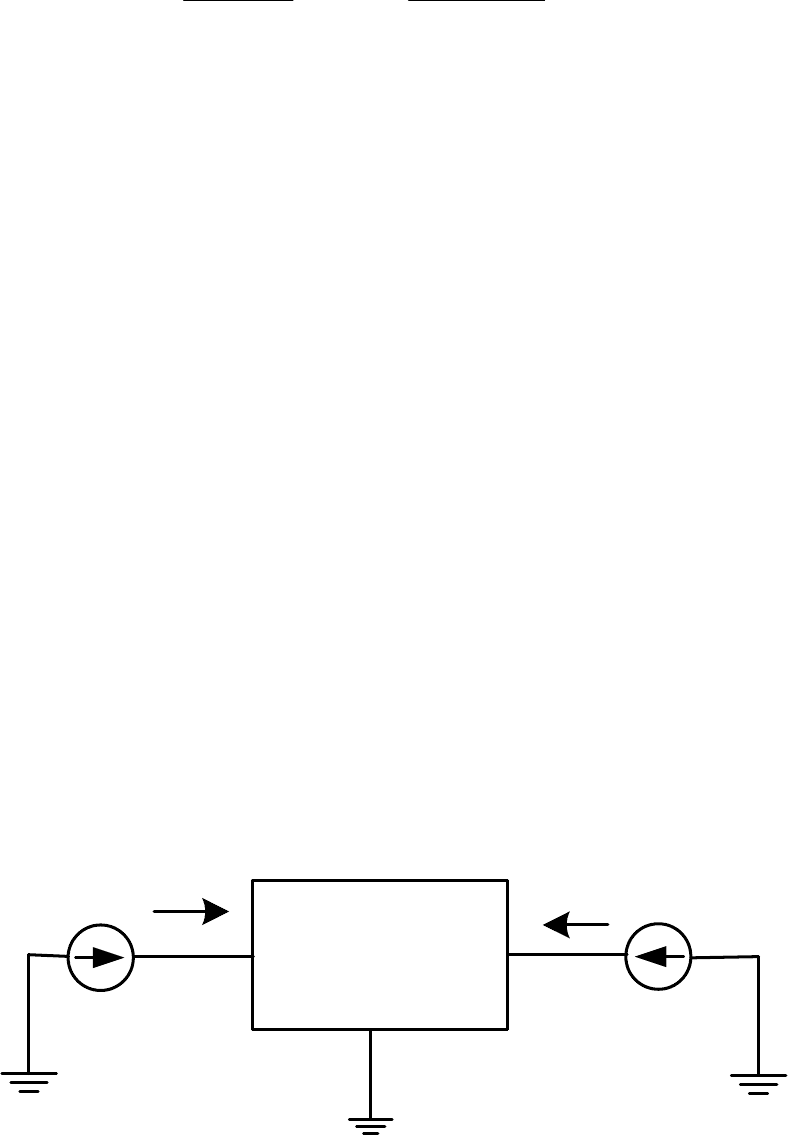
Упрощенная схема замещения системы при оснащении АРВ СД
имеет вид, представленный на рисунке 1.8.6, т.е. представлена проек-
цией напряжения
Г
U
на ось
q
(сопротивление генератора в семе за-
мещения не учитывается).
0.189
−
sin 2.0
δ
⋅
( )
⋅
0.708sin
δ
(
)
⋅
+
0.708cos δ( )⋅ 0.378− cos 2.0 δ⋅( )⋅+ 0
solve δ,
float 3,
0.776i
−
0.776i
1.96−
1.96
→
34
Т
0,44
х
j
Л1
0,716
х
j
0 0
P Q
+
Л2
0,716
х
j
0,97
U
=
Г
q
U
Рисунок 1.8.6 – Схема замещения системы, оснащенной АРВ СД
Определим напряжение на шинах генератора
Г
U
:
12,37
Г вн
1,138 0,25 1,165
j
U U I x j e
°
= + ⋅ = + = ⋅
ɺ ɺ ɺ
,
где
Л1
вн Т
0,807
2
x
x x j= + =
,
Г0
12,37 .
δ = °
Определим проекцию напряжения
Г
U
на ось
q
:
Г Г 0 Г0
cos( ) 1,165 cos(43,735 12,37 ) 0,995.
q
U U
= ⋅ δ −δ = ⋅ °− ° =
Напишем выражение активной мощности по (1.8.12):
Г
2
0,995 0,97 0,97 7,628
( ) sin sin(2 );
0,807 2 8,435 0,807
q
U
P
⋅
δ = ⋅ δ− ⋅ ⋅ δ
⋅
Г
( ) 1,2 sin 0,527 sin(2 )
q
U
P
δ = ⋅ δ− ⋅ δ
Характеристика представлена на рисунке 1.8.4 (верхняя кривая).
Произведем расчеты (рисунок 1.8.7), аналогичные предыдущим с
использованием программы Mathcad.
Рисунок 1.8.7 – Определение максимума функции
Г
( )
q
U
P
δ
Функция имеет максимальное значение при
2,07
рад 118,6
δ = = °
,
при этом
Г
max
1,2 sin(118,6 ) 0,527 sin(2 118,6 ) 1,497.
q
U
P
= ⋅ ° − ⋅ ⋅ ° =
Коэффициент запаса статической устойчивости равен
0.527− sin 2.0 δ⋅( )⋅ 1.2 sin δ(
)
⋅+
1.054− cos 2.0 δ⋅( )⋅ 1.2 cos δ( )⋅+ 0
solve δ,
float 3,
2.07
−
2.07
0.305i−
0.305i
→
35
Г
0
0
1,497 0,3
100% 100% 399%.
0,3
q
q
U
U
P P
K
P
−
−
⋅ = ⋅ =
=
1.9 Характеристика мощности при сложной связи генератора с
системой
Полученная ранее синусоидальная зависимость (1.4.2) активной
мощности от угла нагрузки справедлива для простейшей СЭС с неяв-
нополюсным генератором (турбогенератором), имеющей чисто ин-
дуктивное сопротивление. При этом вся активная мощность, произ-
водимая генератором, поступает в приемную систему. Однако чаще
связь между генератором и приемной системой представляется по-
стоянными активными и реактивными сопротивлениями и мощность,
производимая генератором, не совпадает с мощностью, получаемой
приемной системой.
В общем случае систему (рисунок 1.9.1). можно представить в
виде четырехполюсника (о четырехполюсниках см. приложение 2) с
параметрами
,
A
,
B
,
C
.
D
Эти параметры для типовых схем четы-
рехполюсников можно вычислить по таблице П2.1 приложения 2.
Напряжение приемной системы
U
ɺ
будем рассматривать в качестве
второго источника наравне с ЭДС
.
E
ɺ
2
z
Е
ɺ
U
ɺ
2
I
ɺ
1
I
ɺ
, , ,
A B C D
Рисунок 1.9.1 – Система как четырехполюсник
На основании принципа наложения (принцип наложения форму-
лируется так: ток в любой ветви цепи с неизменными сопротивле-
ниями равен алгебраической сумме токов, создаваемых в этой ветви
каждой из ЭДС в отдельности) для цепи на рисунке 1.9.1 можно запи-
сать

36
1 11 12
;
I EY UY
= −
ɺ ɺ ɺ ɺ ɺ
(1.9.1)
2 22 21
,
I UY EY
= − +
ɺ ɺ ɺ ɺ ɺ
где
11
Y
ɺ
– собственная проводимость цепи первого источника;
12
Y
ɺ
–
взаимная проводимость цепей первого и второго источников;
22
Y
ɺ
–
собственная проводимость цепи второго источника;
21
Y
ɺ
– взаимная
проводимость цепей второго и первого источников.
Собственные проводимости (
11
Y
ɺ
и
22
Y
ɺ
) определяют абсолютное
значение и фазу тока в цепи данного источника (
E
ɺ
или
U
ɺ
) при от-
сутствии ЭДС другого источника.
Взаимные проводимости (
12
Y
ɺ
и
21
Y
ɺ
) определяют абсолютное зна-
чение и фазу тока в цепи данного источника, обусловленного ЭДС
другого источника. При этом всегда
12 21
Y Y
=
ɺ ɺ
.
Учитывая, что комплекс полной мощности равен произведению
комплекса ЭДС на сопряженный комплекс тока (выражение (П3.11)
приложения 3), определим мощность
Г
,
S
ɺ
производимую генератором
и мощность
H
,
S
ɺ
получаемую системой:
Г Г Г 1 11 12 11 12
ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ
( )
S P jQ EI E EY UY EEY EUY
= + = = − = −
ɺ
ɺ ɺ ɺ ɺ
(1.9.2)
H H H 2 22 21 22 21
ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ
( )
S P jQ UI U UY EY UUY UEY
= + = = − + =− −
ɺ
ɺ ɺ ɺ ɺ
(1.9.3)
Г
S
ɺ
представляет собой мощность в точке приложения ЭДС
,
E
ɺ
т.е. внутреннюю мощность за его сопротивлением в семе замещения.
Если принять, что направление вектора напряжения приемной систе-
мы
U
ɺ
совпадает с действительной осью на комплексной плоскости,
то тогда фазный угол вектора
E
ɺ
будет равен углу нагрузки
.
δ
В качестве фазных углов собственных и взаимных сопротивле-
ний четырехполюсника входят углы
11
ψ
,
22
ψ
,
12
ψ
, причем
11
11 11
e
j
Z z= ⋅
ψ
;
22
22 22
e
j
Z z= ⋅
ψ
;
12
12 21 12
e
j
Z Z z= = ⋅
ψ
. (1.9.4)
Углы определяются следующим образом:
11
11
11
arctg
x
r
ψ
=
;
22
22
22
arctg
x
r
ψ
=
;
12
12
12
arctg
x
r
ψ
=
. (1.9.5)
При этом проводимости равны соответственно
11
11 11
e
j
Y y
−
= ⋅
ψ
;
22
22 22
e
j
Y y
−
= ⋅
ψ
;
12
12 12
e
j
Y y
−
= ⋅
ψ
. (1.9.6)
37
Принимая во внимание, что фазные углы сопряженных векторов
должны быть взяты со знаком «минус», получим выражения для
мощностей генератора и приемника:
11 12
11 12
Г Г 11 12
( )2
11 12
e e e e
j jj j j
j j
P jQ E E y E Uy e
E y e EUy e
−
+
+ = − =
= −
ψ ψδ δ δ
ψ δ ψ
(1.9.7)
22 12
22 12
2
H H 22 12
( )2
22 12
e e e
e e
j
j
P jQ U y E Uy
U y EUy
−
− +
+ =− + =
=− +
ψ ψδ
ψ δ ψ
(1.9.8)
или в тригонометрической форме
[
]
[ ]
2
Г Г 11 11 11
12 12 12
cos sin
cos( ) sin( )
P jQ E y j
EUy j
+ = + −
− + + +
ψ ψ
δ ψ δ ψ
[
]
[ ]
2
H H 22 22 22
12 12 12
cos sin
cos( ) sin( ) .
P jQ U y j
EUy j
+ =− + +
+ − + + − +
ψ ψ
δ ψ δ ψ
(1.9.10)
Выделим активную и реактивную мощности
2
Г 11 11 12 12
cos cos( );
P E y EUy
ψ δ ψ
= − +
(1.9.11)
2
H 22 22 12 12
cos cos( );
P U y EUy
ψ δ ψ
=− + − +
(1.9.12)
2
Г 11 11 12 12
sin cos( );
Q E y EUy
ψ δ ψ
= − +
(1.9.13)
2
H 22 22 12 12
sin sin( );
Q U y EUy
ψ δ ψ
=− + − +
(1.9.14)
Если вместо углов
ψ
ввести дополняющие их до 90˚ углы
90
α ψ
= °−
, то выражения запишутся в виде
2
Г 11 11 12 12
sin sin( );
P E y EUy
α δ α
= + −
(1.9.15)
2
H 22 22 12 12
sin sin( );
P U y EUy
α δ α
=− + +
(1.9.16)
2
Г 11 11 12 12
cos cos( );
Q E y EUy
α δ α
= − −
(1.9.17)
2
H 22 22 12 12
cos cos( ).
Q U y EUy
α δ α
=− + +
(1.9.18)
Структура выражений остается при любой связи генератора и
приемника. Изменения схемы влияют только на значения собствен-
ных и взаимных проводимостей и углов
.
α
1.10 Определение собственных и взаимных проводимостей
системы
38
Существует несколько способов определения собственных и вза-
имных проводимостей системы. Некоторые из них мы рассмотрим на
примере.
Пример 1.10.1 Определение проводимостей системы
1) Способ пассивных четырехполюсников
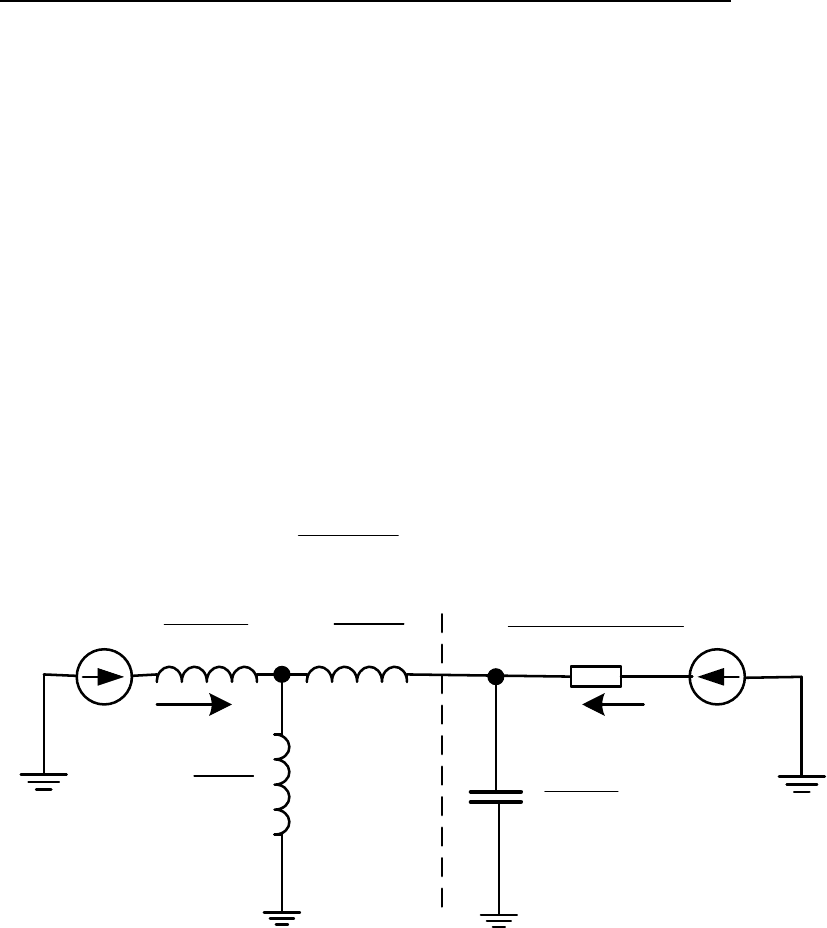
Рассмотрим систему, схема замещения которой представлена на
рисунке 1.3.2. В этой схеме емкостное сопротивление
Л
2
b
x
включено
непосредственно на шины неизменного напряжения
U
и потому не
может оказать влияния на величину искомого эквивалентного сопро-
тивления (проводимости). Оно при расчете сопротивления не должно
приниматься во внимание (см., аналогичный пример, [3], задача 2-3
на с. 25). Влияние этого сопротивления необходимо учитывать при
определении потоков мощности. Объединив индуктивные и активные
сопротивления ЛЭП, получим схему, представленную на рисунке
1.10.1.
Л1 Л1
Л
0,135 0,367
2
x r
z j
+
= = +
ɺ ɺ
ɺ
7,628
d
х
j
Т
0,44
х
j
U
Л
0,213+ 0,358
z
j
Л
1
7,09
b
х
-j
Т
730
х
j
µ
Е
1
I
2
I
b
a
Рисунок 1.10.1 – Схема замещения для расчета собственных
и взаимных проводимостей
Полученную схему разобьем условно пунктирной линией на две
части, тогда в левой части окажется Т-образный четырехполюсник,
состоящий из сопротивлений
T T
, ,
d
x x x
µ
, а в правой Г-образный четы-
рехполюсник из сопротивлений
Л Л
, 1
b
z x
.
По формулам из таблицы П2.1 приложения 2 определим коэффи-
циенты Т-образного четырехполюсника:
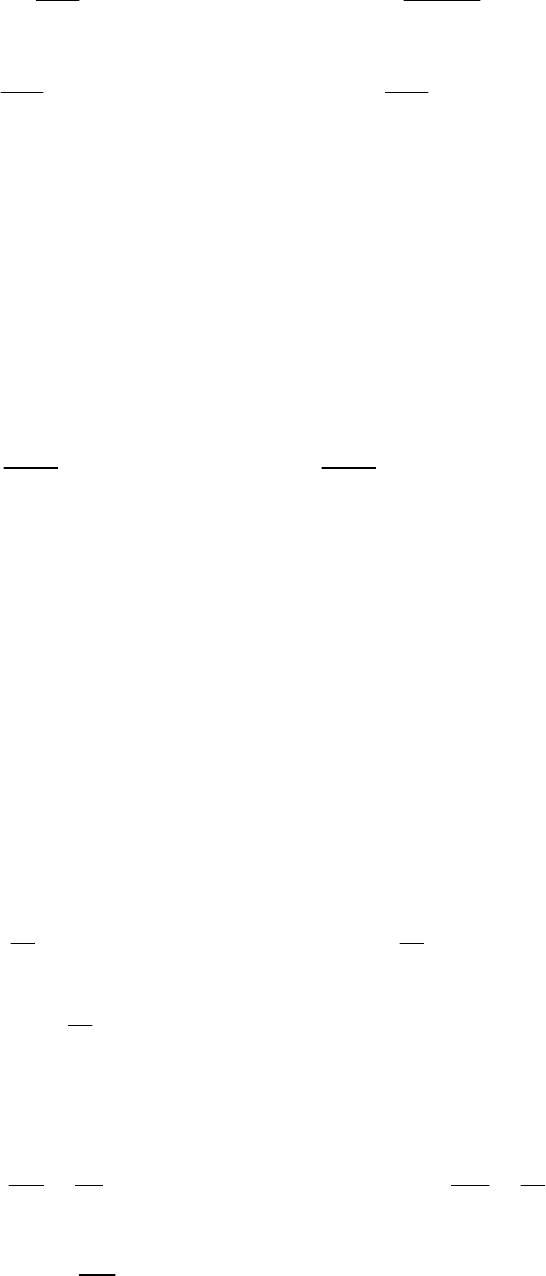
39
1
T
1 1,01;
d
x
A
x
µ
= + =
ɺ
ɺ
ɺ
T
1 T
T
8,073;
d
d
x x
B x x j
x
µ
⋅
= + + =
ɺ ɺ
ɺ
ɺ ɺ
ɺ
1
T
1
0,00137;
C j
x
µ
= = −
ɺ
ɺ
T
1
T
1 1,001.
x
D
x
µ
= + =
ɺ
ɺ
ɺ
Проверку правильности расчетов произведем по формуле (П2.5)
приложения 2:
1 1 1 1
1.
A D B C
⋅ − ⋅ =
ɺ ɺ
ɺ ɺ
Расчет произведен правильно.
Также по формулам из таблицы П2.1 приложения 2 определим
коэффициенты Г-образного четырехполюсника:
2
1;
A
=
ɺ
2 Л
0,135 0,367;
B z j= = +
ɺ
ɺ
2
Л
1
0,138;
1
b
C j
x
= =
ɺ
ɺ
Л
2
Л
0,95 0,019.
1
b
z
D j
x
= = +
ɺ
ɺ
ɺ
Проверка:
2 2 2 2
1.
A D B C
⋅ − ⋅ =
ɺ ɺ
ɺ ɺ
Коэффициенты обобщенного четырехполюсника определим по
формулам (П2.18) приложения 2:
1 2 1 2
0,1;
A A A B C= ⋅ + ⋅ =−
ɺ ɺ ɺ ɺ
ɺ
1 2 1 2
0,013 8,036;
B A B B D j= ⋅ + ⋅ = − +
ɺ
ɺ ɺ ɺ ɺ
1 2 1 2
0,136;
C C A D C j= ⋅ + ⋅ =
ɺ ɺ ɺ ɺ
ɺ
1 2 1 2
0,951 0,018;
D D D C B j= ⋅ + ⋅ = +
ɺ
ɺ ɺ ɺ ɺ
Проверка:
1.
A D B C
⋅ − ⋅ =
ɺ ɺ
ɺ ɺ
Определим проводимости по формулам (П2.19) приложения 2:
11
1
0,0021 0,1183;
Y j
B
= = −
ɺ
ɺ
22
0,00002086 0,0124;
A
Y j
B
= = +
ɺ
ɺ
ɺ
12 21
1
0,0002088 0,1244.
Y Y j
B
= = =− −
ɺ ɺ
ɺ
В некоторых случаях вместо проводимостей удобнее использо-
вать собственные и взаимные сопротивления:
11
11
1
0,149 8,451;
B
Z j
Y D
= = = +
ɺ
ɺ
ɺ ɺ
22
22
1
0,135 80,433;
B
Z j
Y A
= = = −
ɺ
ɺ
ɺ
ɺ
12 21
12
1
0,013 8,036.
Z Z B j
Y
= = = = − +
ɺ ɺ ɺ
ɺ

40
2) Способ единичных токов
Для определения проводимостей по способу единичных токов
необходимо на первом этапе (рисунок 1.10.2
а
) из схемы замещения
исключить второй источник (
U
), закоротив выход системы на землю.
При этом полагаем, что ток на выходе системы равен
0
20
1 e .
j
I
°
= ⋅
ɺ
7,628
d
х
j
Т
0,44
х
j
Л
0,135+ 0,367
z
j
Л
1
7,27
b
х
- j
Т
727
х
j
µ
Е
a
b
1
I
20
1
I
=
U
Л
0,135+ 0,367
z
j
Л
1
7,27
b
х
-j
Т
727
х
j
µ
a
b
10
1
I
=
2
I
a
b
ab
I
0
a
I
0
b
I
Т
0,44
х
j
7,628
d
х
j
ab
I
0
a
I
0
b
I
Рисунок 1.10.2 – Способ единичных токов
Затем производим расчет:
20 Л
1(0,135 0,367) 0,135 0,367;
b
U I z j j= ⋅ = + = +
ɺ ɺ
0
Л
0,05 0,019;
1
b
b
b
U
I j
x
= =− +
ɺ
ɺ
20 0
0,95 0,019;
ab b
I I I j= + = +
ɺ ɺ
T
0,127 0,785;
a b ab
U U I x j= + ⋅ = +
ɺ ɺ ɺ
0
T
0,00209 0,1183;
a
a
U
I j
x
µ
= = −
ɺ
ɺ
1 0
0,951 0,018;
ab a
I I I j= + = +
ɺ ɺ ɺ
1
0,013 8,036;
a d
E U I x j= + ⋅ = − +
ɺ ɺ ɺ
