Белов А.В., Коровин Ю.В. Устойчивость электрических систем

Подождите немного. Документ загружается.

Поскольку в дальнейшем все расчеты будем производить только

в системе относительных единиц, индекс (

∗

) в дальнейшем изложе-

нии опускается.

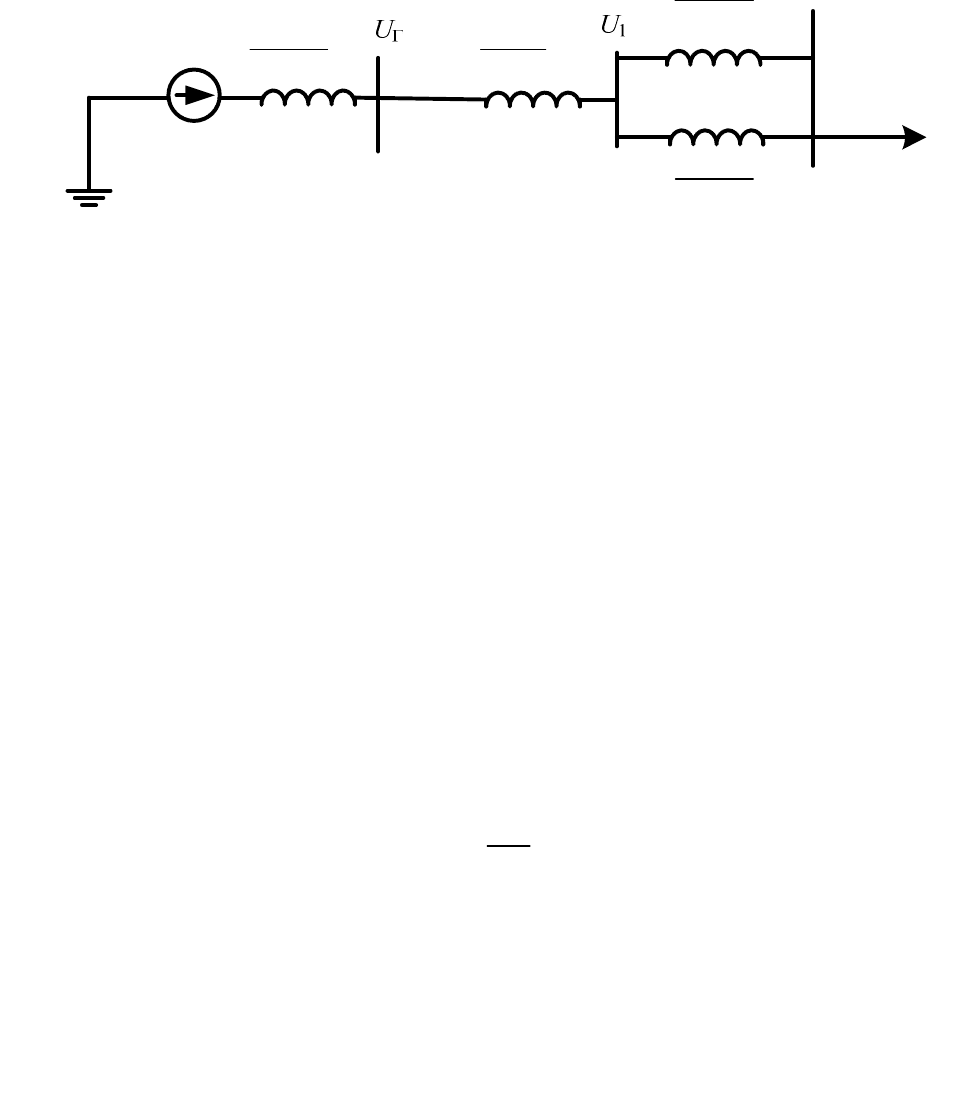
Часто в приблизительных расчетах применяют упрощенную схе-

му замещения, пренебрегая проводимостями и активными сопротив-

лениями (рисунок 1.3.3):

7,628

0,44

Л1

0,734

0 0

P Q

Л2

0,734

0,97

Рисунок 1.3.3 – Упрощенная схема замещения простейшей

электрической системы

В дальнейшем, в зависимости от принятых допущений, будем

принимать для расчета ту или иную схему замещения.

1.4 Характеристика мощности простейшей системы

Под простейшей системой (рисунок 1.1.1) понимается такая, в

которой одиночная электростанция (эквивалентный генератор) свя-

зана посредством трансформаторов и ЛЭП с шинами приемной сис-

темы, мощность которой настолько велика по сравнению с мощно-

стью рассматриваемой электропередачи, что напряжение на шинах

приемной системы можно считать неизменным.

В качестве схемы замещения простейшей системы используем

упрощенную схему, представленную на рисунке 1.1.3.

Определим суммарное сопротивление элементов системы.

Л1

d d

x x x

= + +

ɺ ɺ ɺ

(1.4.1)

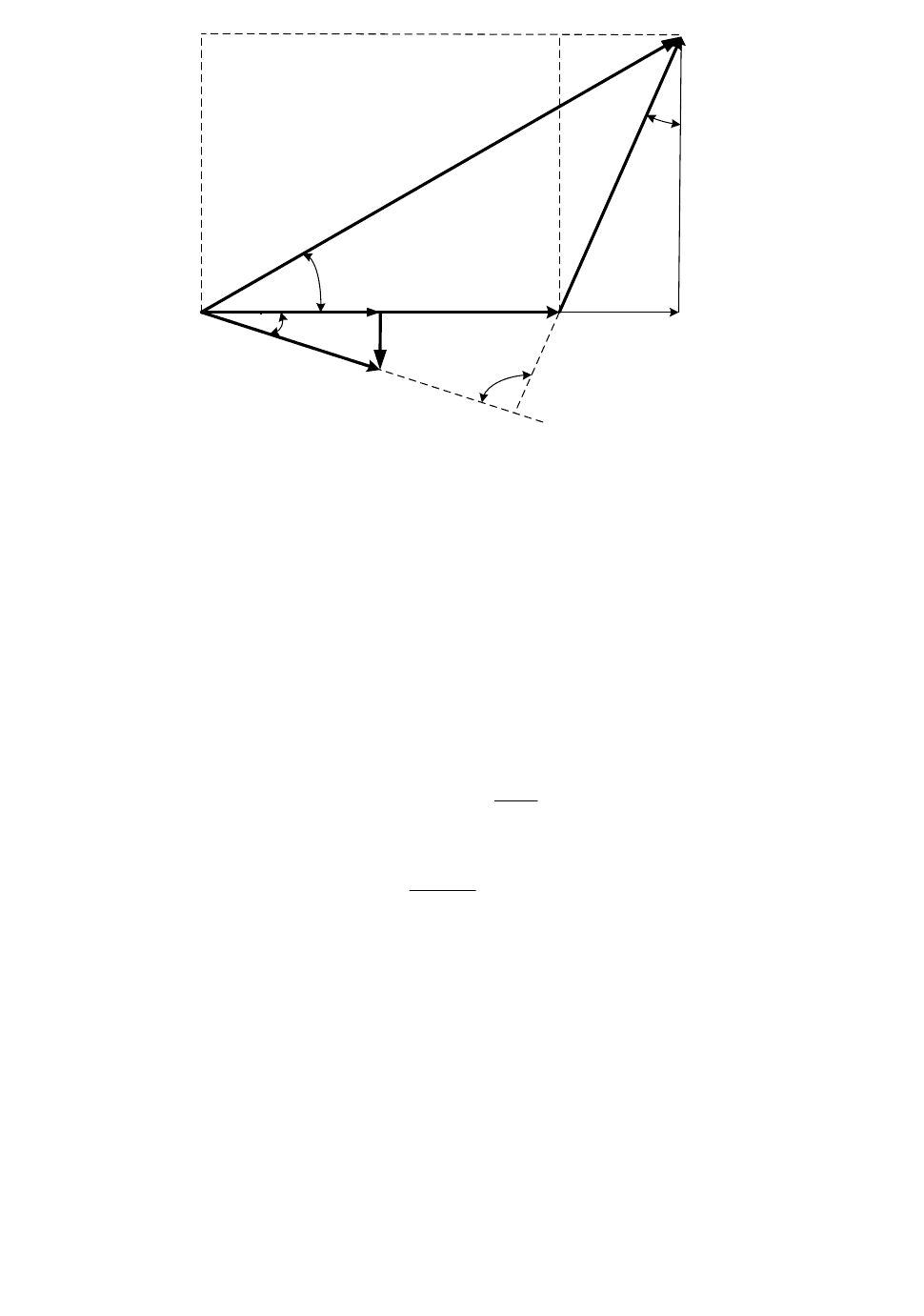
Для получения характеристики мощности построим векторную

диаграмму (рисунок 1.4.1). Для удобства примем, что вектор напря-

жения

на шинах неизменного напряжения совпадает с действи-

тельной осью (осью абсцисс)

(

)

U U

I x

•

I x

Рисунок 1.4.1 – Векторная диаграмма простейшей системы

Из равенства отрезков

sin

OA E

= δ

a d

BC I x

вытекает соот-

ношение

sin

a d q

I x E

= δ

где

– активный ток;

– угол сдвига фаз вектора ЭДС

относи-

тельно вектора напряжения приемной системы

Умножая обе части равенства на

получим:

sin ,

P UI

= = δ

(1.4.2)

где

– активная мощность, выдаваемая генератором.

Зависимость (1.4.2) называется угловой характеристикой мощно-

сти генератора. Она носит синусоидальный характер. При постоянст-

ве тока возбуждения генератора (

const

, если генератор не снаб-

жен автоматическим регулятором тока возбуждения АРВ) ЭДС гене-

ратора

является постоянной величиной. Также постоянным явля-

ется и напряжение

на шинах системы. Таким образом, как следует

из выражения (1.4.2) угол поворота

определяется только активной

мощностью генератора, которая, в свою очередь, определяется мощ-

ностью турбины.

Угол

часто называют углом нагрузки. Аналогию его физиче-

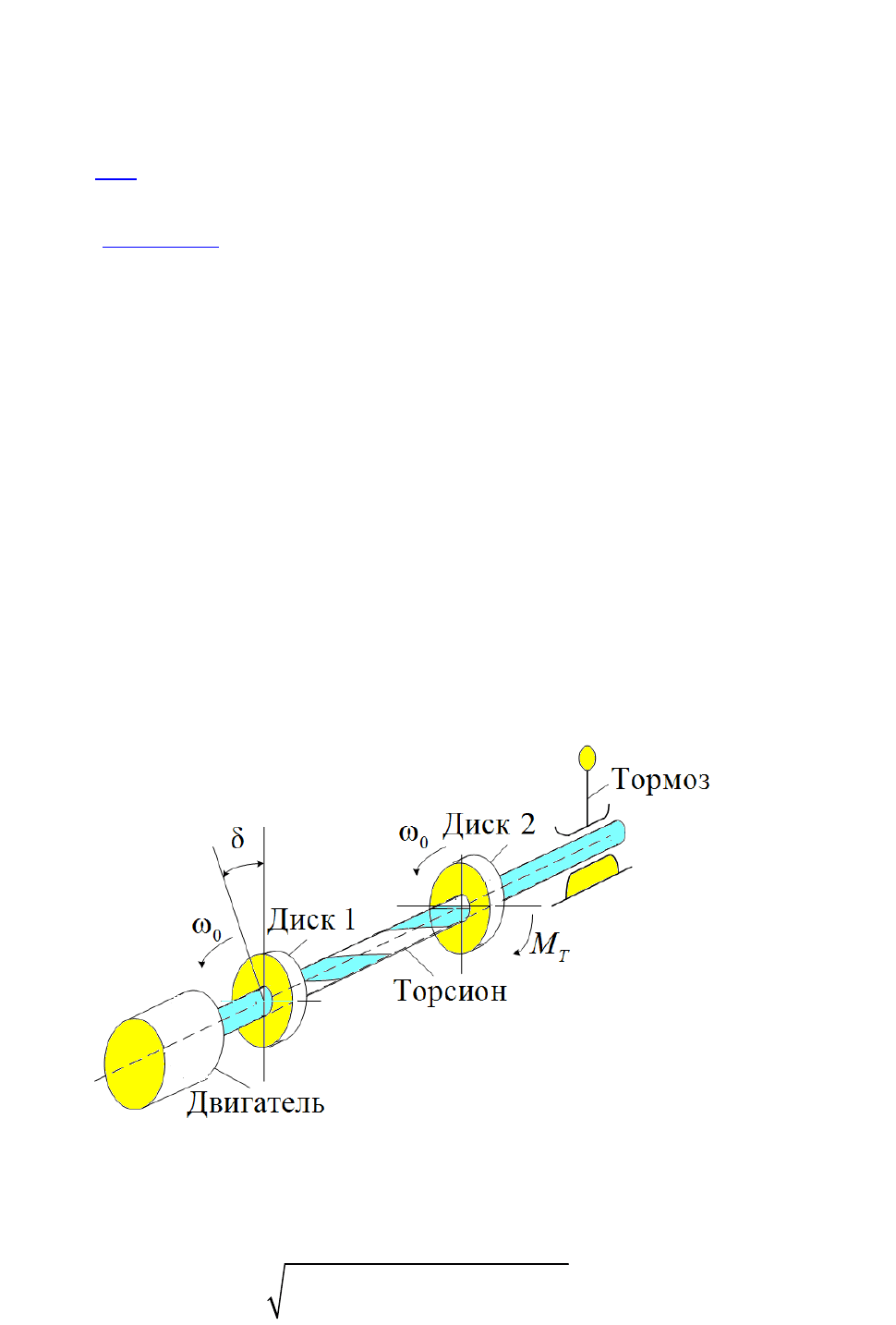
ского смысла можно проиллюстрировать рисунком 1.4.2. Предста-

вим, что некоторый двигатель вращает с синхронной скоростью

диск 1, который через упругий вал - торсион вращает диск 2 [Торси-

он (от фр. torsion — скручивание, кручение) — стержень или вал с

приложенным к его концам крутящим моментом, то есть, работаю-

щий на кручение, который выполняет функции упругого элемента]. В

режиме холостого хода (тормоз отключен) диск 2 вращается син-

хронно с диском 1. При появлении тормозного момента

синхрон-

ность вращения дисков сохранится, однако торсион, испытывая с од-

ной стороны момент вращения двигателя, а с другой стороны тор-

мозной момент, вследствие своей упругости подобно жесткому тросу

повернется на угол

и, следовательно, диск 1 будет опережать диск

2 на этот угол.

С возрастанием тормозного момента торсион будет все больше

скручиваться, и угол

будет увеличиваться. При достижении неко-

торого предельного тормозного момента торсион не выдержит на-

грузки и разрушится, что равносильно потере устойчивости. Таким

образом, угол скручивания торсиона под нагрузкой является механи-

ческим аналогом угла

между ЭДС генератора и напряжением при-

емной системы.

Рисунок 1.4.2 – Механический аналог угла нагрузки

Из диаграммы (рисунок 1.4.1) определим ЭДС

( )

q c p d a d

E U I x I x

Σ Σ

= + +

или

q d d

Q P

E U x x

U U

Σ Σ

 

 

 

= + +

(1.4.3)

При этом, как следует из диаграммы (рисунок 1.4.) угол нагрузки

равен

arctg arctg

x I

U x I

U x

δ = =

(1.4.4)

Можно также определить (это тоже следует из диаграммы) вели-

чину ЭДС

как сумму векторов напряжения

и произведения

(здесь и в дальнейшем будем обозначать комплексы токов, на-

пряжений и мощностей точкой над символом, и комплексы сопро-

тивлений – также точкой над символом):

q d

U I x

= + ⋅

ɺ ɺ

(1.4.5)

Ток в выражении (1.4.5) определим по формуле П3.14 как отно-

шение сопряженного комплекса полной мощности к сопряженному

комплексу напряжения на данном участке (здесь и далее сопряжен-

ные комплексы будем обозначать уголком над символом).

(1.4.6)

Анализ выражения (1.4.2) показывает, что активная мощность,

передаваемая генератором в приемную систему достигает макси-

мального значения при

sin 1

δ =

E U

(1.4.7)

Коэффициент запаса статической устойчивости простейшей сис-

темы по мощности определяется из выражения

100%.

P P

−

⋅

(1.4.8)

Сказанное поясним на примере.

Пример 1.4.1. Определить ЭДС генератора, построить угловую

характеристику и определить коэффициент запаса статической ус-

тойчивости.

В качестве исходной возьмем упрощенную схему замещения (ри-

сунок 1.1.3). Найдем суммарное сопротивление системы по (1.4.1):

Л1

0,734

7,628 0,44 8,435.

2 2

d d

x x x j j j

+ + = + + ==

ɺ ɺ ɺ

Определим ток в системе по выражению (1.4.6):

33,954

0 0 0

€

0,3 0,202

0,309 0,208 0,373 e

€ €

0,97

S P Q

U U

− °

−

= = = − = ⋅=

Определим ЭДС системы по формуле (1.4.5):

43,735

0,97 (0,309 0,208) 8,435 2,727 2,609 3,774

q d

U I x j j j e

= + ⋅ = + − ⋅ = + = ⋅

ɺ ɺ

Из последнего выражения следует, что угол нагрузки при работе

генератора в нормальном режиме равен

43,735 .

δ = °

Запишем выражение угловой характеристики активной мощности

системы при

= const

по формуле (1.4.2):

3,774 0,97

( ) sin sin 0,434 sin .

8,435

E U

⋅

δ δ δ = ⋅ δ

= =

(1.4.9)

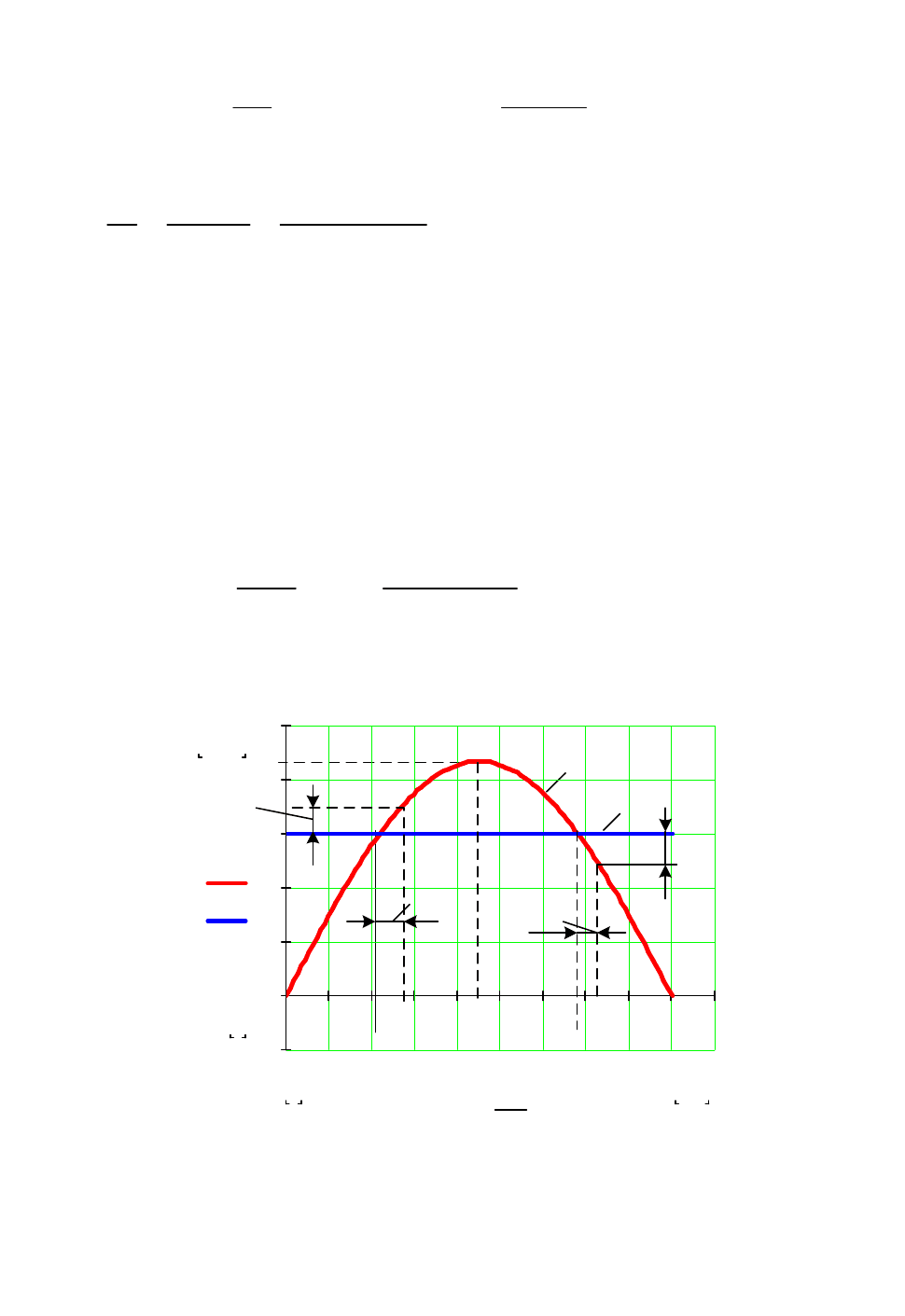
Характеристика представлена на рисунке 1.4.3.

( )

0 20 40 60 80 100 120 140 160 180 200

0.1−

0.1

0.2

0.3

0.4

0.5

0.434

P δ( )

1800

180

⋅

∆δ

∆

∆δ

кр

Рисунок 1.4.3 – Характеристика активной мощности простейшей системы

без АРВ (при постоянстве тока возбуждения)

По выражению (1.4.7) находим величину максимальной переда-

ваемой генератором мощности

0,434.

E U

По выражению (1.4.8) находим коэффициент запаса статической

устойчивости системы по мощности

0,434 0,3

100% 100% 44,7%.

0,3

P P

−

⋅ = ⋅ =

Здесь следует отметить, что для устойчивой эксплуатации систе-

мы необходимо иметь запас статической устойчивости по мощности

не менее 20% в нормальном режиме и 8% – в послеаварийном.

1.5 Критерий статической устойчивости простейшей системы

Мощность, потребляемая приемной системой в нормальном ре-

жиме работы равна

. Из выражения (1.4.2) найдем угол нагрузки,

при котором генератор отдает мощность

в нормальном режиме для

рассмотренного выше примера

0,3 8,435

arcsin arcsin arcsin0,6912 43,728 .

3,774 0,97

P x

E U

⋅

δ = = = = °

⋅ ⋅

Этот результат мы уже получили другим способом в предыдущем

пункте. Горизонтальная прямая пересекает синусоиду дважды за

один период. Нас интересует только следующее пересечение, которое

можно определить по формуле

кр

arcsin .

 

δ = π−

 

 

(1.5.1)

В нашем случае

( )

кр

0,3

arcsin 180 arcsin 0,691 180 43,728 136,232 .

0,434

 

δ = π− = °− = °− °= °

 

 

Итак, характеристика

( )

пересекает линию

в двух точках:

при

43,728

δ = °

и при

кр

136,232

δ = °

. Но только при

режим являет-

ся устойчивым.

Рассмотрим режим работы в точке

(рисунок 1.4.3). Если мощ-

ность генератора по какой-либо причине изменится на величину

∆

то угол

, следуя синусоидальной зависимости, изменится на вели-

чину

∆

. Из графика видно, что в точке

положительному прира-

щению мощности соответствует положительное приращение угла.

Далее при увеличении мощности генератора на валу, связываю-

щего его с турбиной, равновесие моментов нарушается и возникает

избыточный тормозящий момент, т.к. тормозящий момент генератора

преобладает над вращающим моментом турбины. Под влиянием тор-

мозящего момента ротор генератора начинает замедляться, что вызы-

вает перемещение ротора и связанного с ним вектора ЭДС

в сто-

рону уменьшения угла

. (Перемещение ротора под действием избы-

точного момента накладывается на его движение в положительном

направлении с синхронной скоростью, которая во много раз выше

скорости этого перемещения). В итоге в точке

восстанавливается

исходный режим работы и, как следует из определения статической

устойчивости, этот режим является устойчивым. Такой же вывод

можно получить и при уменьшении мощности генератора в точке

В точке

отрицательному приращению мощности генератора

соответствует положительное приращение угла. При уменьшении

мощности генератора на валу возникает ускоряющий избыточный

момент, который увеличивает угол

. С ростом угла мощность гене-

ратора падает, это увеличивает ускоряющий момент, т.е. возникает

лавинообразный процесс, называемый выпадением из синхронизма.

Процесс выпадения из синхронизма и асинхронный режим, в котором

в итоге оказывается генератор, характеризуется непрерывным пере-

мещением вектора

относительно вектора напряжения

приемной

системы.

Если в точке

возникнет тормозной избыточный момент (мощ-

ность генератора увеличится), то он вызовет перемещение рабочей

точки система генератор-турбина в точку

Таким образом, точка

характеристики мощности является точ-

кой устойчивого равновесия, точка

– точкой неустойчивого равно-

весия моментов турбины и генератора. Поэтому все точки, лежащие

на возрастающей части характеристики мощности, являются точками

устойчивой работы системы, а точки, лежащие на падающей части

характеристики, – точками неустойчивой работы.

Границей зон устойчивой и неустойчивой работы является мак-

симум характеристики мощности.

Формальным признаком статической устойчивости электриче-

ской системы может служить знак отношения приращения мощности

к приращению угла. Если

∆

∆δ

, то система устойчива. Переходя к

пределу, можно записать критерий устойчивости:

. (1.5.2)

1.6 Уравнение движения ротора генератора

Незначительное возмущение в цепи статора генератора вызывает

движение ротора в сторону увеличения или уменьшения угла

(это

зависит от знака избыточного момента). Возмущение сообщает рото-

ру некоторое ускорение

, которое в относительных единицах про-

порционально избыточному моменту

∆

и обратно пропорциональ-

но механической постоянной инерции

j j

M P

T T

∗ ∗

∆ ∆

= =

(1.6.1)

Здесь принимается, что при небольших изменениях скорости мо-

мент в относительных единицах равен мощности в относительных

единицах:

∗∗

∆

– механическая постоянная, время, в течение которого ско-

рость ротора изменяется от нуля до номинальной под действием но-

минального избыточного момента сопротивления.

2 2

ГА

ном

2,74

, c

1000

GD n

⋅

(1.6.2)

где

ГА

– маховой момент системы «генератор – приводной двига-

тель (турбина)», т·м

;

– скорость вращения, об/мин;

ном

– номи-

нальная мощность генератора, кВ·А.

2 2 2

ГА Г ПД

GD GD GD

= +

где

– маховой момент генератора, т·м

;

ПД

– маховой мо-

мент турбины, т·м

Возвращаясь к уравнению (1.6.1) и учитывая, что ускорение

представляет собой вторую производную от угла по времени, полу-

чим

d P

dt T

δ ∆

= =

(1.6.3)

и далее

Т эл

T P P

= −

(1.6.4)

где

– мощность турбины, для простейшей системы равна мощно-

сти, передаваемой генератором в приемную систему

Т 0

, выраже-

на в относительных единицах;

эл

– электромагнитная мощность ге-

нератора, зависящая от угла нагрузки и для простейшей системы рав-

ная

эл

sin

P Р

= ⋅ δ

, выражена в относительных единицах.

Уравнение (1.6.4) называется уравнением движения ротора гене-

ратора. Его решение в форме

)(tf

дает картину изменения угла

во времени и позволяет судить об устойчивости генератора.

В выражении (1.6.4) величины

, ,

T t

выражены в радианах.

Здесь следует остановиться на некоторых особенностях примене-

ния системы относительных единиц при решении задач по устойчи-

вости систем.

Время

Время в системе относительных единиц обычно измеряется в ра-

дианах. За базисное время

принимают время, в течение которого

ротор, вращающийся с синхронной угловой скоростью

, повернет-

ся на 1 радиан (

б 0

= ω

). Время в относительных единицах выража-

ется произведением времени (в секундах) на синхронную угловую

скорость ротора

[c]

[c] 0

t t

∗

= = ⋅ω

(1.6.5)

При синхронной частоте тока

Гц

2 314

ω = π⋅ =

, и

[c]

314

t t

∗

= ⋅

(1.6.6)

Угол

Угол поворота ротора измеряется в электрических радианах

эл геом

δ =δ ⋅

(1.6.7)

где

геом

– геометрический угол,

– число пар полюсов генератора.

Соотношения между углами, выраженными в радианах и граду-

сах, могут быть записаны, как

[град] [рад]

180

δ = δ ⋅

[рад] [град]

180

δ =δ ⋅

(1.6.8)

Скорость

Скорость (электрическая) ротора

∆ω

по отношению к синхронно

вращающейся оси (относительная скорость) определяется как раз-

ность фактической электрической скорости

и синхронной скорости

или, что то же, как производная относительного угла во времени:

= ∆ω= ω−ω

(1.6.9)

Относительная электрическая скорость

∆ω

связана с относитель-

ной механической скоростью

∆Ω

соотношением:

∆ω

∆Ω =

(1.6.10)

Относительная электрическая скорость

∆ω

, выраженная в долях

от базисной:

б б б

∗

∆ω

∆ω δ

∆ω = − = ⋅

ω ω ω

(1.6.11)

Так как за базисное значение скорости обычно принимают син-

хронную скорость

, то выражение относительной скорости примет

вид

1 ,

314

∗ ∗

∆ω =ω − = ⋅

(1.6.12)

где

– в радианах,

– в секундах.

Если

принять в градусах, а

– в секундах, то

18000

∗

∆ω = ⋅

(1.6.13)

Мощность и момент

Электромагнитная мощность связана с моментом и механической

скоростью соотношением

P M

= Ω⋅

или в относительных единицах

P M

∗ ∗ ∗

=ω ⋅

(1.6.14)

Подставив

∗

из (1.22), получим

1 .

1800

P M

∗ ∗

 

 

= + ⋅

 

 

(1.6.15)