Белов А.В., Коровин Ю.В. Устойчивость электрических систем

Подождите немного. Документ загружается.

Министерство сельского хозяйства Российской Федерации

Департамент научно-технологической политики и образования

ФГОУ ВПО «Челябинская государственная агроинженерная

академия»

Белов А.В., Коровин Ю.В

УСТОЙЧИВОСТЬ

ЭЛЕКТРИЧЕСКИХ СИСТЕМ

Учебное пособие

Челябинск

2010

УДК 621.311(07)

Белов А.В., Коровин Ю.В. Устойчивость электрических систем:

Учебное пособие.

Рассмотрены практические методы расчёта устойчивости элек-

трических стистем. Приведены основные допущения, изложены ос-

новы и порядок расчета в системе относительных единиц, принципы

определения параметров элементов, составление и преобразование

схем замещения. Пособие содержит примеры расчёта, варианты зада-

ния и необходимый справочный материал. В пособии использованы

учебные и методические наработки кафедры «Электрические стан-

ции, сети и системы» ЮУрГУ.

Пособие предназначено для студентов V курса факультета элек-

трификации и автоматизации сельскохозяйственного производства

ЧГАА, обучающихся по направлению подготовки 140200 – «Элек-

троэнергетика».

Рецензенты

Пястолов В.В. – канд. техн. наук, доцент (ЮУрГУ)

Знаев А.С. – канд. техн. наук, доцент (ЧГАУ)

Печатается по решению редакционно-издательского совета ЧГАУ

ISBN 978-5-88-88156-

верситет», 2010.

ВВЕДЕНИЕ

Аварии, связанные с нарушением устойчивости параллельной ра-

боты генераторов в крупных электроэнергетических системах (в

дальнейшем – электрических системах), влекут за собой расстройство

электроснабжения больших районов и городов. Ликвидация таких

аварий и восстановление нормальных условий работы электрических

систем представляют большие трудности и требуют много времени.

При сравнительно небольшом числе аварий, их последствия

весьма тяжелы, что заставляет уделять значительное внимание во-

просам увеличения устойчивости как при проектировании электриче-

ских станций и сетей, так и при их эксплуатации.

Различают статическую и динамическую устойчивость. Матема-

тические приемы, используемые для их анализа, между собой суще-

ственно отличны. Сложность расчетов требует применения соответ-

ствующих средств вычислительной техники. В настоящем пособии

примеры расчетов приведены как правило, с использованием про-

граммы Mathcad.

Пособие содержит задание для выполнения контрольной работы

(приложение 4).

Целью контрольной работы является приобретение навыков

расчета статической и динамической устойчивости, а также навыков

применения программы Mathcad для расчетов устойчивости электри-

ческих систем.

Глава 1 Статическая устойчивость

1.1 Основные понятия и определения

В установившемся режиме реальной системы электропередачи

его параметры постоянно меняются, что связано с изменением на-

грузки, изменением схемы коммутации, включением и отключением

отдельных генераторов. Эти изменения соответствуют установивше-

муся режиму и поэтому называются малыми возмущениями.

Таким образом, всегда имеются малые возмущения параметров

режима, при которых она должна быть устойчива.

Нарушение устойчивости в электрических системах всегда за-

канчивается появлением асинхронного хода, связанного с неограни-

ченным изменением скоростей вращения синхронных машин, и при-

водит к отключению нагрузки, генераторов станций и т.д.

Статическая устойчивость – это способность системы восста-

навливать исходный (или близкий к исходному) режим после малого

его возмущения.

Большими возмущениями называются такие, которые происхо-

дят при КЗ, аварийных отключениях генераторов или линий и т.п.

Под действием больших возмущений возникают резкие изменения

режима.

Динамическая устойчивость – это способность системы воз-

вращаться в исходное состояние (или близкое к нему) после большо-

го возмущения.

Когда после большого возмущения синхронный режим наруша-

ется, а затем восстанавливается, то говорят о результирующей устой-

чивости.

Результирующая устойчивость – это способность системы са-

мопроизвольно возвращаться в длительно существующий устано-

вившийся режим после кратковременного нарушения устойчивости.

Если выпавшая из синхронизма система после устранения при-

чины вновь втягивается в синхронизм, то считают, что система с под-

ключенными к ней генераторами обладает результирующей устойчи-

востью. Результирующую устойчивость часто считают разновидно-

стью динамической устойчивости.

Пропускной способностью элемента системы в установившемся

режиме называется наибольшая мощность, которую можно передать

через этот элемент с учетом всех ограничивающих факторов (нагрева,

устойчивости, напряжения в узлах и т.д.) Иногда пропускную спо-

собность определяют по одному фактору, например, пропускная спо-

собность по нагреву и т.д.

Деление на статическую и динамическую устойчивость вызвано,

прежде всего, особенностью математических приемов, которые ис-

пользуют для анализа устойчивости.

Например, анализ статической устойчивости рассматривается

при «малых» возмущениях (отклонениях) параметров режима от их

установившихся значений (обычно в пределах линейных изменений),

что дает возможность линеаризовать модель электрической систе-

мы, тогда как анализ динамической и результирующей устойчивости

выполняется только с использованием нелинейных моделей. При

этом математическая постановка задачи и ее решение значительно

усложняются.

1.2 Допущения, принимаемые при анализе устойчивости, задачи

анализа

Кроме допущений, принятых при анализе электромагнитных пе-

реходных процессов, принимаются еще несколько, упрощающих

оценку устойчивости при удовлетворительной точности.

1. Предполагается, что скорость вращения роторов синхронных

машин при электромеханических процессах изменяется в небольших

пределах (2...3%) синхронной скорости.

2. Считается, что напряжение и токи статора и ротора генератора

изменяются мгновенно.

3. Нелинейность параметров системы обычно не учитывается

(Параметры системы – сопротивления, проводимости, коэффициенты

трансформации, постоянные времени). Нелинейность параметров ре-

жима, наоборот, учитывается (Параметры режима – напряжения,

мощности, токи и т.п. Параметры режима связаны между собой пара-

метрами системы). Когда от такой нелинейности отказываются, то

это специально оговаривают и систему называют линеаризован-

ной.

4. Перейти от одного режима электрической системы к другому

можно, изменив собственные и взаимные сопротивления схемы, а

также ЭДС генераторов и двигателей.

5. Исследование динамической устойчивости при несимметрич-

ных возмущениях производится в схеме замещения прямой последо-

вательности. Считается, что движение роторов генераторов и двига-

телей обусловлено моментами, создаваемыми токами прямой после-

довательности.

Задачами анализа статической устойчивости являются:

1. Расчет параметров предельных режимов (предел передаваемой

мощности, предельное (критическое) напряжение в узловых точках

системы, питающих нагрузку и т.п.).

2. Определение коэффициентов запаса устойчивости по напряже-

нию и мощности.

3. Выбор мероприятий по повышению статической устойчивости

энергосистем или обеспечению заданной пропускной способности

передачи.

4. Разработка требований, направленных на улучшение устойчи-

вости систем. Выбирается настройка АВР, обеспечивающая требуе-

мую точность поддержания напряжения.

Задачами анализа динамической устойчивости являются:

1. Расчет параметров динамического перехода при эксплуатаци-

онном или аварийном отключениях нагруженных элементов электри-

ческой системы.

2. Определение параметров динамических переходов при корот-

ких замыканиях в системе с учетом различных факторов:

– возможного перехода одного несимметричного КЗ в другое

(например, однофазного в двухфазное);

– работы автоматического повторного включения элемента, от-

ключившегося после КЗ;

Результатами расчета динамической устойчивости являются:

– предельное время отключения расчетного КЗ в наиболее опас-

ных точках электрической системы;

– паузы систем АПВ, установленных на различных элементах

электрической системы;

– параметры систем автоматического ввода резерва (АВР).

1.3 Составление схемы замещения и определение её параметров

Расчет устойчивости системы начинается с составления схемы

замещения и определения её параметров. Расчет параметров произво-

дится, как правило, в системе относительных единиц. При определе-

нии параметров используются рекомендации, изложенные в прило-

жении 1, а также математические формулы, известные из курса элек-

тромагнитных переходных процессов [9, 10].

Пример 1.3.1 Определение параметров схемы замещения

0 0

cos

Рисунок 1.3.1 – Расчетная схема простейшей электрической системы

Дана

простейшая

электрическая

система

(

рисунок

1.3.1).

– 2

генератора

типа

ТВФ

-120-2

Гном

100

МВт;

Гном

125

МВ A;

= ⋅

Гном

cos

0,8;

Гном

10,5

кВ;

(ном)

1,907;

(ном)

0,278;

′

2 2

т м ;

= ⋅

– 2

трансформатора

типа

ТДЦ

-125000/330;

Tном

125

МВ A;

= ⋅

347

кВ;

10,5

кВ;

790

кВт;

∆ =

11,0%;

0,55%;

2 –

двухцепная

линия

электропередачи

300

км;

330

кВ

–

напряжение

на

шинах

системы

неизменного

напря

жения

;

0 0 0

;

S P

300M

Вт;

cos

0,83

–

нагрузка

передаваемая

от

генератора

приемную

систему

неизменного

напряжения

нор

мальном

режиме

Необходимо

составить

схему

замещения

определить

её

пара

метры

соответствии

рекомендациями

изложенными

приложе

нии

составим

схему

замещения

(

рисунок

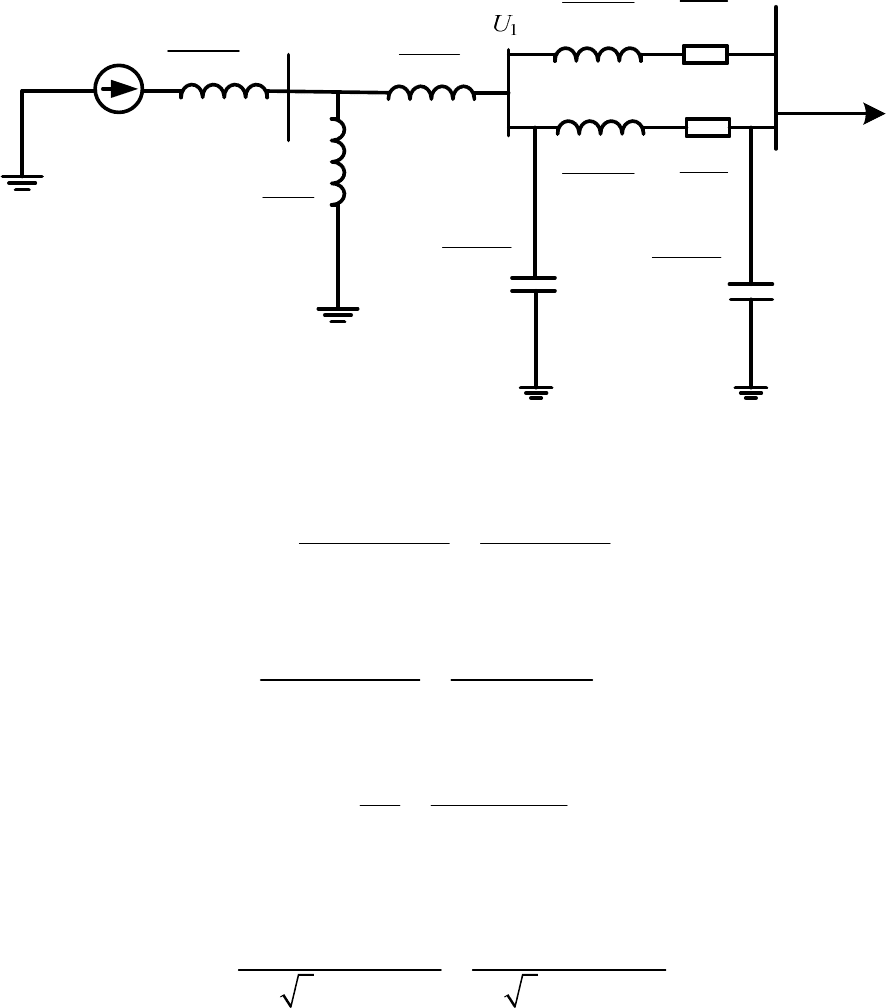
1.3.2).

качестве

базисных

примем

1000

МВ А;

= ⋅

340

кВ.

Определим

общие

сопротивления

двух

генераторов

включенных

параллельно

(ном) б

Гном

1,907 1000

7,628

2 125

;

x S

n S

∗

⋅

= =

⋅ ⋅

(ном) б

Гном

0,278 1000

1,112

2 125

x S

n S

∗

′

⋅

= =

⋅ ⋅

′

где

–

количество

генераторов

7,628

0,44

Л1

0,734

727

Л1

0,27

ВЛ

- 7,27

BЛ

- 7,27

0 0

P Q

Л2

0,27

Л2

0,734

0,97

Рисунок 1.3.2 – Схема замещения простейшей электрической системы

Сопротивление и проводимость трансформаторов

к б

Тном

11,0 1000

0,44

100 100 2 125

u S

n S

∗

⋅

= =

⋅ ⋅ ⋅ ⋅

где

– количество трансформаторов.

Тном

2 0,55 125

0,00137

100 100 1000

;

n I S

µ∗

⋅ ⋅

= =−

⋅ ⋅

или в пересчете на сопротивление

1 1

727

0,00137

;

b j

µ∗

= =

−

Исходя из объема передаваемой мощности, получаем, что ток в

линии электропередачи должен составлять в пересчете на одну цепь

300000

316A.

3 cos 2 3 330 0,83

N U

= =

⋅ ⋅ ⋅ ϕ ⋅ ⋅ ⋅

где

– количество цепей в линии электропередачи.

Задавшись временем использования максимальной нагрузки в го-

ду

макс

4000

, определим по известным таблицам экономическую

плотность тока

эк

1,1

А/мм

При заданном номинальном напряжении, с целью уменьшения

потерь на корону и снижения индуктивного сопротивления, провод в

каждой фазе расщепляют на два (

). Определим сечение каждого

из расщеплённых проводов

пр

эк

316

143,7

мм .

1,1 2

J n

= =

⋅ ⋅

Принимаем провод АС-150. Тогда общее сечение проводов в це-

пи одной фазы будет

Ц пр

300

мм .

2 150 2

F= ⋅ = ⋅ =

Радиус такого провода фазы сечением

300

мм

равен

пр

300

9,772

мм

3,14

R = = =

Определим эквивалентный радиус расщепленного на два провода

фазы (см. приложение 1):

Э2 пр

9,772 300 54,144

мм

R R а= ⋅ = ⋅ =

где

300

мм

– расстояние между двумя расщепленными проводами

одной фазы.

Расстояние между фазными проводами (изоляционное расстоя-

ние по воздуху) примем по рекомендациям [11, таблица 6-4] равным

3500

мм.

АВ

Кроме того, необходимо выдержать необходимое безо-

пасное расстояние от проводов до ближайших частей опоры (для ли-

ний напряжением 330 кВ оно составляет не менее 2,8 м [11, п.6-1]).

Приняв, что провода одной цепи будут располагаться по одну сторо-

ну опоры, а провода другой цепи – по другую, примем окончательно

АВ

3500

мм,

ВС

3500

мм,

АС

7000

мм,

(последнее расстояние

получилось в два раза большим, т.к. все три провода находятся по

одну сторону от опоры.

Среднее расстояние между проводами

ср АВ ВС СА

3500 3500 7000 4410

мм.

D D D D= ⋅ ⋅ = ⋅ ⋅ =

Погонное индуктивное сопротивление одной цепи определим по

выражению (П1.12) с учетом сопротивления и числа расщепленных

проводов

ср

пог

Э2

0,016 4410 0,016

0,144 lg = 0,283

Ом/км

48,3 2

0,144 lg ;

R n

+ = ⋅ +

= ⋅

а общее сопротивление одной цепи линии электропередачи в относи-

тельных единицах

1 Л2 пог

2 2

ср.ном

1000

0,276 300 = 0,734.

340

x x

j j

х L

∗ ∗

= ⋅

= = ⋅

ɺ ɺ

Погонную емкостную проводимость одной цепи определим по

выражению (П1.7)

6 6

пог

ср

Э2

7,58 10 7,58 10

= 3,967 10

См км.

4410

54,144

− −

−

⋅ ⋅

= ⋅ ⋅

Общая емкостная проводимость для двух цепей ЛЭП

2 3,967 10 300 0,00238

См,

j j

N b L

−

= ⋅ ⋅ ⋅ =

= ⋅ ⋅

где

– количество цепей в линии электропередачи.

Эта проводимость носит рассредоточенный характер, поэтому

разделим её на две части – в начале и в конце линии, и найдем значе-

ние каждой части в пересчете на сопротивление в относительных

единицах

Л Л

2 2

ср.ном

2 2 1000

7,27.

0,00238 340

1 2

b b

U j

х х

∗ ∗

= = ⋅ =−

= ⋅

ɺ ɺ

Погонное активное сопротивление провода одной цепи рассчита-

ем, исходя из значения удельной проводимости алюминия

32 м/ОмЧ

мм

пог

0,000104

Ом/м = 0,104 Ом/км.

32 300

= =

γ ⋅ ⋅

Общее активное сопротивление одной цепи в относительных

единицах составляет

Л1 Л2 пог

2 2

ср.ном

1000

0,104 300 0,27.

340

r r L

= ⋅ ⋅ = ⋅ =

Напряжение на шинах неизменного напряжения в относительных

единицах

330

0,97.

340

∗

= =

Мощность, поступающая от генераторов на шины неизменного

напряжения в относительных единицах

300

0,3;

1000S

∗

= =

0 0 0

tg 0,3 0,672 0,202,

Q P

∗ ∗

⋅ ϕ = ⋅ =

здесь

0 0

arccos(0,83) 33,9 ; tg tg(33,9 ) 0,672.

ϕ = = ° ϕ = ° =