Бауэрс Н., Гербер Х., Джанс Д., Несбитт С., Хикман Дж. Актуарная математика
Подождите немного. Документ загружается.


20.5.
Нарастание
актуарных
обязательств
541
fw(r)lrar/EJ.
Разность
между
настоящими
стоимостями
этих
двух
бессрочных
анну
итетов
равна
настоящей
стоимости
(rA)t
будущих
пенсионных
выплат
замкнутой
группе
участников
схемы,
которые
в
настоящий
момент
не
моложе
r
лет.
~
20.5.
Нарастание
актуарных
обязательств
Методы
актуарных
расходов
различаются
той
скоростью,
с
которой
будущие
пенсионные
обязательства
нарастают
в
течение
периода
трудовой
активности
участ
ников
пенсионной
схемЫ.
Метод
конечных
расходов,
описанный
в
разд.
20.3,
не
пре
дусматривает
возникновения
обязательств
до
самого
момента
наступления
пенси
онного
возраста
т.
Для
того
чтобы
выразить
нарастание
актуарных
обязательств
в
случае
пенсий,
вьtплаты
которых
начинаются
в
возрасте
т,
для
любого
метода
расхо
дов
мы
определим
фу'Н:к:цию
нараста'Н,ия
обязательств
М
(х).
Она
равна
той
доле
актуарной
настоящеit
стоимости
будущих
пенсионных
выплат,
которая
наросла
в
виде
актуарных
обязательств
к
моменту
достижения
возраста
х
при
использовании
данного
метода
актуарных
расходов.
Функция
М(х)
-
неубывающая
непрерывная
справа
функция
аргумента
х,
возраста,
такая,
что
О
~
М(х)
~
1
для
всех
х
~
а.
При
'Н,а'чдл'Ь'Но.м
финансировании
все
обязательства
по
будущим
пенсионным
выплатам
принимаются
в
полном
объеме
сразу,
как
только
участник
пенсионной
схемы
всту
пил
в
нее
в
возрасте
а
лет,
так
что
М(х)
==
О
для
х
<
а
и
М(х)
==
1
для
х
~
а.
Для
других
методов
актуарных
расходов
предполагается,
что
М
(а)
==
О.
Для
методов
финансирования,
требующих
нарастания
или
признания
обязательств
относительно
будущих
пенсионных
выплат
в
полном
объеме
к
возрасту
r
лет,
М
(х)
==
1
при
х
~
т.
Функцию
М
(х)
можно
также
определить
в
терминах
фУН~'ЦtJ.и
плотности
на
растания
обязательств
по
nснсия.м,
обозначаемой
через
т(х),
такой,
что
М(х)
=
1.'
m(у)
dy,
х
~
а.
(20.5.1)
Заметим,
что
существует
аналогия
между
функциями
М(х)
и
т(х),
с
одной
сто
роны,
и
функцией
распределения
Fx(x)
и
функцией
плотности
fx(x)
,
с
другой.
В
общем
случае
мы
предполагаем,
что
функция
т(х)
непрерывна
для
а
<
х
<
т,
непрерывна
справа
в
точке
а
и
слева
в
точке
r
и
что
т(х)
==
О
для
х
>
Т.
В
этом
непрерывном
случае
из
формулы
(20.5.1)
следует,
что
т(х)
==
М'(х).
(20.5.2)
в
точках
разрыва
производной
М'(х)
функция
плотности
т(х)
не
определена,
и
мы
можем
придать
ей
произвольное
значение,
например,
равное
правому
или
левому
пределу.
Польза
от
введения
функции
нарастания
обязательств
состоит
в
том,
что
это
позволяет
развивать
теорию
пенсионного
обеспечения
одновременно
для
всего
мно
жества
методов
актуарных
расходов,
а
не
для
каждого
метода
в
отдельности.
Пример
20.5.1.
Пусть
М(х)
==
aa:x-al/aa:r-al'
а
<
х
<
Т.
Проверим,
что
(а)
М
(х)
обладает
свойствами
функции
нарастания
обязательств,
(Ь)
М(Х)
r-xlax
равна
резерву
на
момент
наступления
возраста
х
непрерывно
го
отсроченного
аннуитета,
заключенного
лицом
(а),
с
выплатой
размера
1
в
год,
начиная
с
возраста
т,
оплаченного
непрерывно
выплачиваемыми
премиями.

542
Гл.
20.
Теория
финансирования
пенсионных
схем
Решение.
(а)
М(х)
=
f:
е-о(у-а)в(у)
dy/
f:
е-
6
(у-а)в(у)
dy.
Таким
образом,
М'(х)
=
т(х)
=
е-
6
(ж-а)
s(x)
/
1"
e-
6
(y-a)s(y) dy. (20.5.3)
Далее,
поскольку
М(а)
=
О
и
М(Т)
=1,
ясно,
что
М(х)
обладает
свойствами
функ
ции
нарастания
обязательств.
(Ь)
Резерв
в
возрасте
х,
вычисленный
по
ретроспективной
формуле,
равен
- _ -
r-al
l1
a _
ж-аЕа
r-жlliж
l1
а
:
ж
-
а
l
-
М(
)
P(r-аlаа)Sа:ж-аl
= -
Sа:ж-аl
= -
Е
=
r-жlаж
х.
...
aa:r-al aa:r-al
ж-а
а
20.6.
Основные
актуарные
функции
для
работающих
в
этом
разделе
определим
несколько
актуарных
функций,
связанных
с
финан
сированием
пенсионнь~х
выплат
в
модельной
пенсионной
схеме.
Они
относятся
к
,
работающим
участникам
схемы,
что
будет
обозначаться
префиксом
а
1
).
20.6.1.
Актуарная
настоящая
стоимость
(aA)t
будущих
пенсионных
выплат
Взнос
n(t-x+a)s(x)
участников
схемы,
находящихся
в
возрасте
между
х
и
x+dx
годами
в
момент
времени
t,
рассчитанный
по
методу
конечного
финансирования
в
конце
(Т
-
х)-го
года,
равен
ТР
t
+
r
_
Ж
dx.
Следовательно,
(aA)t =
1"
е-
6
(r-ж)
TPt+r-ж
dx. (20.6.1)
Пример
20.6.1.
Покажем,
что
d
dt (aA)t =
e-O(T~a)
TP
t
+
r
_
a
-
TP
t
+
б(аА)t,
(20.6.2)
и
дадим
словесную
интерпретацию
этого
равенства.
Решение.
Вновь
заметим,
что
д
Т
д
Т
at
Рt+r-ж
= -
дх
Рt+r-ж.
(20.6.3)
Таким
образом,
d
jT
д
jr
д
(
А)
-
-о(r-ж)
Тр,
d -
-б(r-ж)
Тр,
d
dt
а
t -
а
е
at
t+r-ж
Х
- -
а
е
дх
t+r-ж
Х
__
е-
t5
(r-ж)
Тр,
jж=r
+
~
jT
Тп
е-о(r-ж)
dx
-
t+r-ж
и
Гt+r-ж
ж=а
а
=
TPt+r_ae-б(r-а)
-
TP
t
+
б(аА)t.
Скорость
изменения
актуарной
настоящей
стоимости
будущих
пенсионных выплат
равна
настоящей
стоимости
будущего
уровня
нормальных
расходов
при
конечном
финансировании
для
новых
участников
схемы
(которые
выйдут
на
пенсию
через
r -
а
лет)
минус
уровень
нормальных
расходов
при
конечном
финансировании
для
работающих
участников
схемы,
выходящих
на
пенсию
сейчас,
плюс
интенсивность
l)OT
cactive
•.
-
Прu,м.
ред.

20.6.
Основные
актуарные
функции
для
работающих
543
(20.6.4)
начисления
процента,
умноженная
на
актуарную
настоЯIЦУЮ
стоимость
на
момент
времени
t.
~
20.6.2.
Уровень
нормальных
расходов
P
t
Предположим,
что
был
выбран
метод
актуарных
расходов
с
функцией
нарас
тания
обязательств
М
(х).
Мы
хотим
найти
формулу
для
уровня
нормальных
рас
ходов
в
модельной
пенсионной
схеме,
т.
е.
найти
такую
функцию,
которая
в
нашей
непрерывной
модели
выражает
актуарную
настояIЦj'Ю
стоимость
будущих
пенсион
ных
выплат
через
величины,
относящиеся
к
различным
моментам
периода
трудовой
деятельности
участника
пенсионной
схемы.
Как
и
в
формуле
(20.6.1),
будущие
нормальные
расходы
при
конечном
финан
сировании
для
участников
пенсионной
схемы
в
возрасте
между
х и х
+
dx
в
момент
времени
t
равны
Tp
t
+
r
_
x
dx.
В
функции
нормальных
расходов
эти
обязательства
учитываются
с
плотностью
т(х).
Мы
имеем
Р,
=
/."
е-б(r-х)
TP'+r_x
m(х)
dx
=
е
Т
'
fw(r)s(r)ii~
/."
е-(б-т)(r-Х)n(t
_
х
+
а)m(х)
dx.
Можно
наглядно
представить,
как
уровень
нормальных
расходов
P
t
,
и
:::;
t
:::;
u+т-а,
полностью
обеспечивает
пенсионные
выплаты
участника
схемы,
вступившего
в
нее
в
возрасте
а
лет
в
момент
времени
и
и
вышедшего
на
пенсию
спустя
r - а
лет.
Рассмотрим
участников
схемы,
которые
вступили
в
нее
между
моментами
времени
u
и
u+du.
Их
окончательный
уровень
нормальных
расходов,
рассчитанный
по методу
конечного
финансирования,
равен
ТР
U
+
Т
_
а
'
В
момент
времени
t
плотность
взносов
этой
группы
в
интеграле,
определяющем
P
t
,
имеет
вид
е-О(Т-Х)
Tp
t
+
r
_
x
т(х),
где
х
=
а
+t -
и.
За
r -
х
лет,
оставшихся
до
выхода
на
пенсию,
эта
величина
возрастет
(в
силу
начисления
процента)
до
величины
Tp
t
+
r
_
x
т(х),
(20.6.5)
и
эта
плотность
в
терминах
u
составит
~Pи+T-a
m(a+t-u).
Интегрируя
эти
взносы,
накопленные
с
учетом
процента,
получим
величину
методе
конечного
/.
и+т-а
и
ТР
u
+
т
_
а
т(а
+ t -
и)
dt
=
ТР
U
+
Т
_
а
'
искомым
уровнем
нормальных
расходов
при
которая
является
финансирования.
Пример
20.6.2.
(а)
Покажем,
что
в
экспоненциальном
случае
D
-о[т-х(в)]
Тр,
rt
=
е
t+r-Х(fJ),
где
В
=
д
-
р
=
д
-
т
- R
и
еОХ(О)
=
/."
m(x)eoxdx.
(Ь)
Дадим
интерпретацию
этой
формулы.
(20.6.6)
(20.6.7)

544
Гл.
20.
Теория
финансирования
пенсионных
схем
Решение.
(а)
Из
формулы
(20.6.4)
и
решения примера
20.3.1
мы
получим
P
t
=/."
e-
6
(r-x)
Tp
t
+
r
_
x
т(х)
dx
=/."
e-
6
(r-x)
TPt+[X(O)-х]+r-Х(О)
т(х)
dx
_/.Т
e-б(r-Х)еР[Х(О)-Х]
Тр,
т(х)
dx
-
t+r-X(O)
а
=
e[-6r+рХ(О)]
TPt+r_X(O)
/.r
е(6-р)х
т(х)
dx.
Сделаем
подстановку
р
=
б
- 8
и,
используя
(20.6.7),
получим
равенство
Р.
-
е[
-бr+(б-О)Х(О)]
То
е{}Х(О)
t -
rt+r-X({})
,
которое
сводится
к
(20.6.6).
(Ь)
Годового
уровня
нормальных
расходов
в
момент
времени
t
с
учетом
про
центов
достаточно
ДЛЯ
обеспечения
уровня
нормальных
расходов,
рассчитанного
по
методу
конечного
финансирования,
спустя
r -
Х
(8)
лет.
Существование
такого
чис
ла
Х
(8)
обеспечивается
теоремой
о
среднем
значении
для
интегралов
и
может
ин
терпретироваться
как
средний
возраст
выплаты
нормальных
расходов,
связанный
с
функцией
плотности
нарастания
обязательств
т(х)
в
экспоненциальном
случае
при
8 =
б
-
т
- R.
Следовательно,
число
Х(8)
зависит
от
процентной
ставки
и
от
скорости
изменения
заработной
платы
и численности
населения.
~
20.6.3.
Актуарные
наросшие
обязательства
(aV)t
Как
и
в
разд.
20.6.2,
будем
предполагать,
что
выбран
метод
актуарных
расхо
дов
с
функцией
нарастания
обязательств
М(х).
По
аналогии
с
(20.6.4)
а7Стуар'Н'Ые
'Наросшие
обязате'//''Ьства
по
отношению
к
работающим
участникам
схемы
в
момент
времени
t
заданы
формулой
(aV)t
=
/."
e-
6
(r-x)
TPt+r_xM(x)
dx.
(20.6.8)
В
этом
интеграле
мы
опирались
на
то,
что
в
виде
актуарных
обязательств
к
возрасту
х
лет
наросла
доля
М(х)
актуарной
настоящей
стоимости
будущих
пенсионных
выплат.
Если
переписать
формулу
(20.6.4)
в
виде
pt =
/."
e-
6
(r-x)
Tp
t
+
r
_
x
dM(x)
и
проинтегрировать
ее
по
частям,
мы
получим,
используя
равенство
(20.6.3),
P
t
=
e-
6
(r-x)
Tp
t
+
r
_
x
М(х{::
-
б
/."
M(x)e-
6
(r-x)
Tp
t
+
r
_
x
dx
+/."
M(x)e-
6
(r-x)
:t
Tp
t
+
r
_
x
dx =
TP
t
-
б(аV)t
+
~
(aV)t,
или
P
t
+
б(аV)t
=
TP
t
+
~
(aV)t.
(20.6.9)
Последнее
равенство
можно
интерпретировать
с
позиций
теории
сложных
процен
тов.
Рассмотрим
актуарные
наросшие
обязательства
(aV)t
как
фонд,
в
который

20.6.
Основные
актуарные
функции
для
работающих
545
поступают
нормальные
расходы
уровня
P
t
и
из
которого
отчисляются
нормальные
расходы
уровня
Tp
t
,
когда
работающие
участники
схемы
выходят
на
пенсию.
Левая
часть
формулы
(20.6.9)
является
скоростью
увеличения
фонда
за
счет
нормальных
расходов
и
процентов.
Правая
часть
представляет
сумму
уровня
нормальных
рас
ходов,
рассчитанного по
методу
конечного
финансирования,
и
скорости
изменения
величины
фонда.
Пример
20.6.3.
Покажем,
что
в
экспоненциальном
случае
(20.6.13)
(20.6.10)
(20.6.11)
(20.6.12)
(а)
(Ь)
(с)
(d)
P
t
+
u
=
epup
t
,
Р
=
т
+ R,
(aV)t+u = epU(aV)t,
P
t
+ O(aV)t =
Tp
t
,
(1
=
д
-
р,
P
t
<
Tp
t
,
если
()
>
О,
P
t
=
Tp
t
,
если
()
=
О,
P
t
>
Tp
t
,
если
8 <
О.
Решение.
(а)
В
примере
20.3.1
показано,
что
Tp
t
+
u
=
ери
TP
t
.
Тогда,
подставляя
это
выражение
в
формулу
(20.6.4),
получим
D
jr
-б(r-х)
Тп
( ) d
ри
jr
-6(т-х)
Тр,
( ) d
ри
D
rt+u =
а
е
Tt+u+r-x
т
х х
=
е
а
е
t+r-x
т
х
х
=
е
rt·
(Ь)
Решение
начинается
с
определения
величины
(aV)t
по
формуле
(20.6.8),
а
дальше
нужно
рассуждать,
как
в
п.
(а).
(с)
Перепишем
равенство
(20.6.11)
в
виде
[(aV)t+u -
(aV)t]/u
=
(ери
-
l)(aV)t/u
и
при
и
-+
О
получим
d
dt (aV)t = p(aV)t. (20.6.14)
Подставляя
это
равенство
в
формулу
(20.6.9),
приходим
к
формуле
(20.6.12).
(d)
Указанные
неравенства
следуют
из
(20.6.12).
Этот
при
мер
снова
показывает
критическую
роль
величины
8 =
д
-
т
- R
в
экспоненциальном
случае.
"
В
соответствии
с
предположением,
что
М(х)
= 1
для
х
;?:
r,
не
существует
будущих
нормальных
расходов
в
отношении
замкнутой
группы
пенсионеров
в
мо
мент
времени
t.
Поэтому
актуарные
наросшие
обязательства
(rV)t
по
отношению
к
участникам
схемы,
вышедшим
на
пенсию,
равны
актуарной
настоящей
стоимости
их
будущих
пенсиЙ.
Таким
образом,
(20.6.15)
Это
приводит
К
следующему
дифференциальному
уравнению
для
актуарных
нарос
ших
обязательств
по
отношению
к
вышедшим
на
пенеию:
(20.6.16)
20.6.4.
Актуарная
настоящая
стоимость
будущих
нормальных
расходов
(Pa)t
В
разд.
20.6.1
мы
заметили,
что
взнос
n(t
-
х
+
а)в(х)
участников
схемы,
нахо
дящихся
в
возрасте
между
х
и
х
+
dx
годами
в
момент
времени
t,
рассчитанный
по
методу
конечного
финансирования,
в
конце
(х
-
r)-ro
года
равен
Tp
t
+
r
_
x
dx.
Когда
18
-
18.1.1
546
Гл.
20.
Теория
финансирования
пенсионных
схем
эти
участники
из
возраста
у
переходят
в
возраст
у
+
dy,
выплачиваются
нормальные
расходы
е-О(Т-У)
Tp
t
+
r
_
x
dxm(y)
dy.
Настоящая
стоимость
этих
нормальных
расхо
дов
равна
е-О(Т-Х)
Tp
t
+
r
_
x
dx
m(у)
dy, (20.6.17)
а
настоящая
стоимость
будущих
нормальных
расходов
для
всех
работающих
участ
ников
схемы,
обозначаемая
через
(Pa)t,
выражается
формулой
(Ра),
=
!.'
e-
6
(r-x)
TPt+r-х
l
'
т(у)
dydx,
(20.6.18)
или
(Ра),
= e
r
'
fw(r)s(r)a~
!.'
e-(6-r)(r-x)n(t
-
х
+
а)[1
-
М(х)]
dx. (20.6.19)
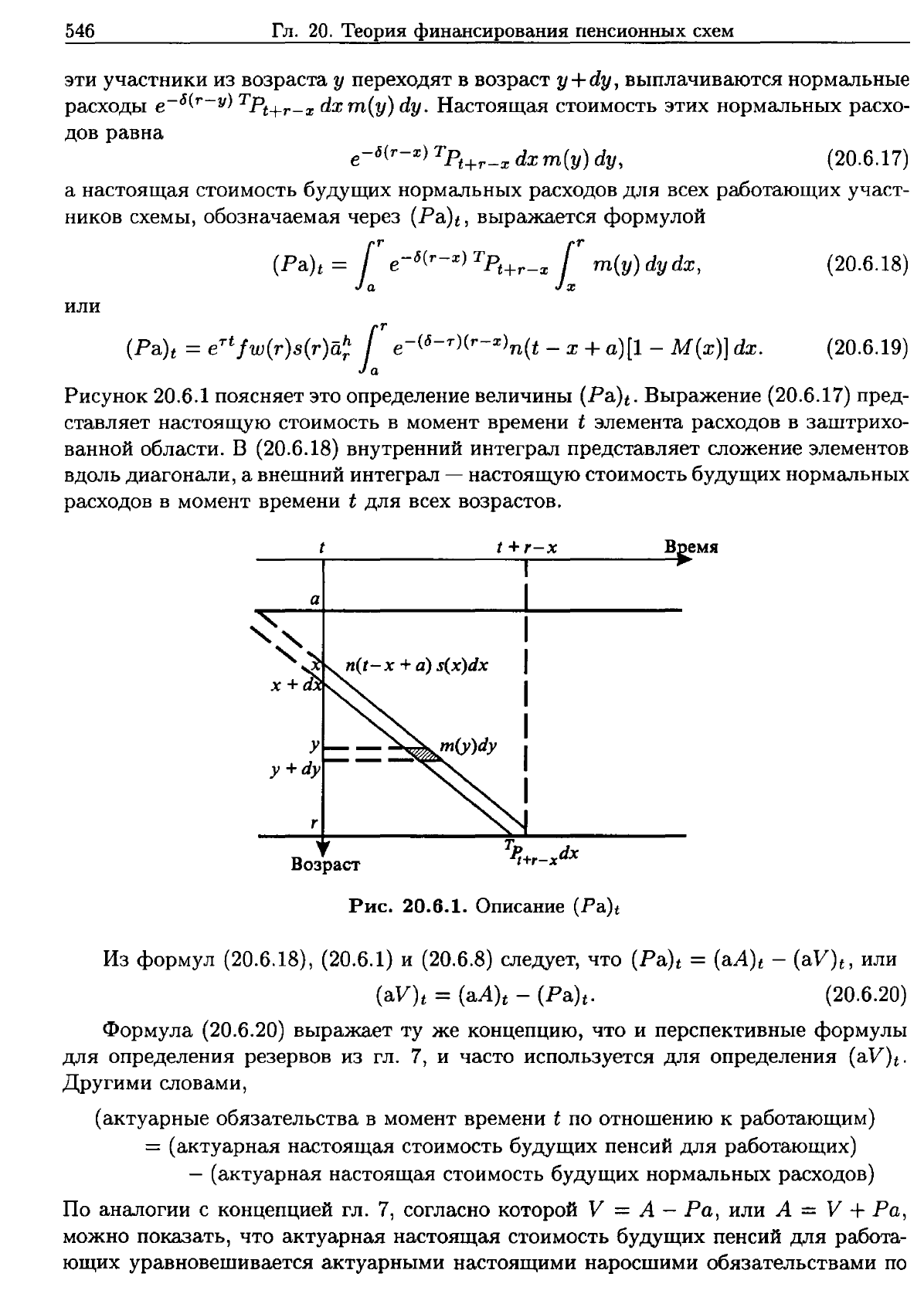
Рисунок
20.6.1
поясняет
это
определение
величины
(Pa)t.
Выражение
(20.6.17)
пред
ставляет
настоящую
стоимость
в
момент
времени
t
элемента
расходов
в
заштрихо
ванной
области.
В
(20.6.18)
внутренний
интеграл
представляет
сложение
элементов
вдоль
диагонали,
а
внешний
интеграл
-
настоящую
стоимость
будущих
нормальных
расходов
в
момент
времени
t
для
всех возрастов.
t
а
""
"
х+
Возраст
t
+г-х
в
емя
Рис.
20.6.1.
Описание
(Pa)t
Из
формул
(20.6.18), (20.6.1)
и
(20.6.8)
следует,
что
(Pa)t =(aA)t - (aV)t,
или
(aV)t = (aA)t - (Pa)t. (20.6.20)
Формула
(20.6.20)
выражает
ту
же
концепцию,
что
и
перспективные
формулы
для
определения
резервов
из
гл.
7,
и
часто
используется
для
определения
(а
V)t
.
Другими
словами,
(актуарные
обязательства
в
момент
времени
t
по
отношению
к
работающим)
=
(актуарная
настоящая
стоимость
будущих
пенсий
для работающих)
-
(актуарная
настоящая
стоимость
будущих
нормальных
расходов)
По
аналогии
с
концепцией
гл.
7,
согласно
которой
V =
А
-
Ра,
или
А
= V +
Ра,
можно
показать,
что
актуарная
настоящая
стоимость
будущих
пенсий
для
работа
ющих
уравновешивается
актуарными
настоящими
наросшими
обязательствами
по

20.7.
Методы
индивидуальных
актуарных
расходов
547
отношению
к
работающим
и
актуарной
настоящей
стоимостью
будущих
нормальных
расходов,
т.
е.
(20.6.21)
Доли
двух
слагаемых
в
правой
части
формулы
(20.6.21)
определяются
мето
дом
актуарных
расходов,
выбранным
в
соответствии
с
функцией
нарастания
обяза
тельств
М(х).
Пример
20.6.4.
(а)
Рассмотрим
две
функции
нарастания
обязательств
М[(х)
и
мп(х).
Покажем,
что
если
величина
П(х)
=
М[(х)
-
Мп(х)
такова,
что
п'(а)
>
О
и
уравнение
п'
(х)
=
о
имеет
в
точности
одно
решение
при
а
<
х
<
т,
то
(а
V)
It
>
-(аV)Пt.
(Ь)
Покажем,
что
если
М[(х)
=
aa:x-al/aa:r-al
и
Мп(х)
=
(х
-
а)/(т
-
а),
то
(aV)It
>
-(аV)Пt.
Решение.
(а)
Согласно
свойствам
функции
нарастания
обязательств,
п(а)
=
п(т)
=
О.
Нам
дано,
что
п'(а)
>
О
и
п'(х)
=
О
в
точности
для
одного
значения
х,
такого,
что
а
<
х
<
т,
а
следовательно,
п(х)
>
О
для
а
<
Х
<
т.
Таким
образом,
выражение
(aV)1t -
(aV)m
=
/."
e-o(r-x)
TPt+r-хD(х)
dx
больше
нуля
и
неравенство
доказано.
(Ь)
Имеем
,
е-о(х-а)в(х)
1
D
(х)
=
---"-r
---....:.-;.-
Ja
е-
6
(у-а)в(у)
dy
r -
а
Далее,
если
б
> 1,
то
е-
6
(у-а)
в(у)
< 1
и,
таким
образом,
/."
e-o(y-a)s(y) dy <
/."
dy = r _
а.
Следовательно,
D'
(а)
=
1"
о(
1 ) 1 >
О.
а
е-
у-а
в(у)
dy
т
-
а
Аналогично,
D'(r) <
О.
Поскольку
как
е-о(х-а)
,
так
и
в(х)
-
убывающие,
но
по
ложительные
функции
от
Х,
П"(х)
<
О, и,
таким
образом,
равенство
D'(x)
=
О
выполняется
в
точности
для
одного
значения
х,
такого,
что
а
<
х
<
т.
Тогда
из
п.
(а)
следует
неравенство
(aV)1t >
-(аV)Пt.
Кроме
того,
в
силу
формулы
(20.6.21)
(aA)t =
(aV)It
+
(Ра)и
=
(аV)Пt
+
(Ра)Пt,
так
что
(Ра)Пt
> (Pa)1t.
20.7.
Методы
индивидуальных
актуарных
расходов
Общий
метод
актуарных
расходов,
задаваемый
функцией
нарастания
обяза
тельств
М
(х)
или
ее
производной
,
функцией
плотности
нарастания
обязательств
т(х),
является
методом
индивидуальных
расходов
в
том
смысле,
что
т(х)
и
М(х)
......

548
Гл.
20.
Теория
финансирования
пенсионных
схем
(20.7.1)
(аА)(х)
=
е-
6
(r-ж)
:~:~
a~,
•
уровень
нормальных
расходов
задается
формулой
можно
применить
для
получения уровня
нормальных
расходов
и
актуарных
нарос
ших
обязательств
по
отношению
к
каждому
участнику
пенсионной
схемы.
Суммар
ный
уровень
нормальных
расходов
и
актуарные
наросшие
обязательства
по
отно
шению
ко всем
работающим
можно
определить
путем
сложения
компонент,
относя
щихся
к
каждому
участнику.
Актуарные
функции,
связанные
с
фиксированием
индивидуальных
пенсий
в
форме
аннуитета
с
начальной
годовой
выплатой
размера
1,
выплачиваемого
с
воз
раста
r
лет,
для
работающих
возраста
х
лет,
а
:::;;
х
:S;
т,
определяются
следующим
образом:
•
актуарная
настоящая
стоимость
будущих
пенсионных
выплат
задается
фор
мулой
Р(х)
=
(аА)(х)m(х),
(20.7.2)
•
актуарные
наросшие
обязательства
задаются
формулой
(aV)(x) =
(аА)(х)М(х),
(20.7.3)
•
актуарная
настоящая
стоимость
будущих
нормальных
расходов
задается
фор
мулой
(Ра)(х)
=
(аА)(х)
- (aV)(x) =
(аА)(х)(1
-
М(х)].
(20.7.4)
Заметим,
что
это
-
показатели,
соответствующие
выплате
размера
1
для
ли
ца
(х),
а
не
суммарные
показатели
для
пенсионной
схемы
на
момент
времени
t.
В
упр.
20.18
подробно
излагаются
соотношения
между
этими
показателями
и
основ
ными
показателями,
касающимися
всей
группы
населения,
которые
рассматрива
лись
в
разд.
20.6.
В
.методах
нарастающих
расходов
на
обеспечение
nенсионн'ых
выплат
функция
М
(х)
непосредственно
связана
с
наросшими
расходами
на
пенсионные
выплаты,
которые
относятся
к
участнику
пенсионной
схемы
в
возрасте
х
лет.
Мы
рассмотрим
две
возможности.
Если
прогнозируемые
обязательства
нарастают
в
течение
периода
трудоспособности
равномерно,
то
m(х)
=
1/(т
-
а)
. (20.7.5)
(20.7.6)
(20.7.7)
Если
нарастание
пенсионных
выплат
пропорционально
сумме
полной
заработной
платы
при
экспоненциальном
временн6м
тренде
роста
всех
заработных
плат,
то
w(х)е
ТЖ
m(х)
=
kw(х)е
ТЖ
= r .
Ja
w(y)e
TY
dy
Частный
случай,
когда нарастание
пенсионных
выплат
пропорционально
сумме
пол
ной
заработной
платы
без
учета
временн6го
тренда
роста
заработной
платы,
т. е.
т::::::
О,
дает
формулу
ш(х)
т(х)
=kw(x) = l
r
()
.
а
W
у
dy
Для
методов
а7'Стуарн'Ых
расходов,
нарастающих
с
.момента
встуnленtL.Я
в
nен
сионную
схему,
прогнозируемые
пенсионные
выплаты
обеспечиваются
постоянными
взносами
с
момента
вступления
в
пенеионную
схему
до
момента
выхода
на
пенеию.

20.7.
Методы
индивидуальных
актуарных
расходов
549
Вновь
рассмотрим
две
возможности.
Если
предположить,
что
уровень
нормальных
расходов
Р(х),
заданный
равенством
(20.7.2),
постоянен,
то
Р(х)
=k =
(аА)(х)т(х)
,
так
что
k ks(x)
-ож
т(х)
=
(аА)(х)
е-о(r-Ж)s(r)а~
=k
1
s(x)e .
Теперь
необходимо
нормировать
т(х),
поскольку
интеграл
по х
ОТ
этой
функции
в
пределах
от
а
до
r
должен
быть
равен
единице:
s(х)е-
ОЖ
т(х)
=
J.r'
(20.7.8)
а
в(у)е-
ОУ
dy
С
другой
стороны,
если
величина
взноса
является
постоянной
долей
1г
от
величи
ны
заработной
платы,
причем
существует
экспоненциальный
тренд
роста
суммарной
заработной
платы,
то
Р(х)
=
1Гw(х)е
ТЖ
=
т(х)(аА)(х),
так
что
е-ОЖ
s(х)еТЖw(х)
m(х)
=
J.r
. (20.7.9)
а
е-ау
в(у
)eTYw(y)
dy
Актуарные
наросшие
обязательства
по
отношению
к
лицам
возраста
х
лет,
т.
е.
раз
ность
между
актуарными
настоящими
стоимостями
пенсионных
выплат
и
будущих
взносов,
равны
(aV)(x) =
е-
6
(Т-Х)
в(т)
jj,h
_
1г
(r
е-6(у-х)
В(У)
w(y)
dy
в(х)
r
Jж
в(х)
=
е-о(r-ж)
в(т)
a~
[1
_
J~
e-ОУs(у)w(у)
d
Y
] =
(аА)(х)М(х).
в(х)
Ja
e-oys(y)w(y)
dy
Это
еще
раз
говорит
в
пользу
нашего
выбора
функции
т(х)
из
формулы
(20.7.9).
Как
и
выше,
можно
показать,
что
если
экспоненциального
временного
тренда
заработной
платы
не
предполагается,
то
функция
плотности
нарастающих
обяза
тельств
~
это
( )
s(х)w(х)е-ОЖ
т
х
=
J:
s(y)w(y)e-
OY
dy
. (20.7.10)
Заметим,
что
доля
прогнозируемых
пенсионных
выплат,
соответствующая
ак
туарным
обязательствам по
методам
актуарных
расходов,
нарастающих
с
момента
вступления
в
пенсионную
схему,
отличается
от
пенсионных
выплат
в
большинстве
схем.
Определение
нарастающих
расходов
на
обеспечение
пенсионных
выплат
необ
ходимо
для
целей
регулирования
и
для
информирования
участников
схемы
о
разме
ре
пенсии,
которая
будет
им
назначена.
Различие
здесь
аналогично
различию
между
резервом
и
выкупной
суммой
в
обычном
страховании.
Следует
также
заметить,
что
ставка
взносов,
выплачиваемых
вкладчиком
схе
мы,
который
придерживается
метода
индивидуальных
актуарных
расходов,
обычно
отличается
от
суммарного
уровня
нормальных
расходов,
определенного
этим
мето
дом.
Это
объясняется
двумя
общими
причинами.
Во-первых,
при
создании
схемы
или
в
момент
пересмотра
правил
схемы
актуарные
наросшие
обязательства
за
пре
дыдущий
период
работы
могут
измениться.
Во-вторых,
актуарные
предположения
не
реализуются
в
точности,
а
следовательно,
возникают
доходы
и
убытки.
Вопрос

550
Гл.
20.
Теория
финансирования
пенсионных
схем
о том,
какие
поправки
следует
внести
в
оценку
ставки
взносов
для
финансового
обеспечения
этих
изменений
актуарных
нарастающих
обязательств
(т.
е.
для
-учета
доходов
или
убытков),
является
важным
и
подлежит
регулированию.
Выбранные
частные
поправки
не
соотносятся
с
выбором
метода
индивидуальных
актуарных
расходов.
20.8.
Методы
групповых актуарных
расходов
В
этом
разделе
рассмотрим
методы
агрегированных
или
групповых
актуарных
расходов,
для
которых
взносы
определяются
на
коллективной
основе,
а
не
как
сум
мы
взносов
от
лица
отдельных
участников.
Чтобы
определить
методы
групповых
актуарных
расходов,
нам
необходимы
три
дополнительных
функции:
1.
(aF)t -
величина
фонда
для
работающих
участников
в
момент
времени
t,
2.
(aC)t
-
поступление
годового
взноса
в
момент
времени
t
для
работающих
участников,
3.
(aU)t -
необеспеченные
актуарные
наросшие
обязательства
(долг)
по
отно
шению
к
работающим
участникам
схемы
в
момент
времени
t.
Таким
образом,
(20.8.1)
Фонд
для
работающих
в
момент
времени
t
можно
описать
дифференциальным
урав
нением
d
т
dt (aF)t = (aC)t + 8(aF)t - P
t
(20.8.2)
с
начальным
значением
(аР)о.
Правая
часть
уравнения
(20.8.2)
отражает
два
источ
ника
поступлений
и
один
источник
расходов
-
перечисление
расходов
на
конечное
финансирование
в
фонд
для
вышедших
на
пенеию.
Если
P
t
-
уровень
нормальных
расходов,
рассчитанный
по
методу
актуарных
расходов
с
некоторой
функцией
нарастания
обязательств
[см.(20.6.4)],
и
(aU)t -
необеспеченные
дополнительные
обязательства
по
отношению
к
работающим
[см.(20.6.8)
и
(20.8.1)],
то
естественно
представить
поступление
взносов
в
следую
щем
виде:
(aC)t = P
t
+
л(t)(аU)t
. (20.8.3)
В
этой
формуле
функция
л(t)
определяет
процесс
погашения
долга
(aU)t.
Равенство
(20.8.3)
указывает
на
еще
не
сформулированную
характеристику
ме
тода
групповых актуарных
расходов.
Эти
методы
определяют
поступление
годового
взноса
(aC)t,
что
зависит
от
финансирования,
т.
е.
от
величины
(aU)t.
Здесь
поправ
ки,
необходимые
для
учета
изменений
правил
схемы
или
доходов
и убытков,
могут
быть
произведены
автоматически
в
рамках
метода
актуарных
расходов,
поскольку
величина
(aU)t
будет
отражать
такие
изменения
и
наличие
доходов
и
убытков.
Рассмотрим
пример
одного
такого
процесс
а
погашения
долга,
для
которого
(20.8.4)
где
ap
t
=
(Pa)t/
P
t
.
(20.8.5)
Таким
образом,
(Pa)t = P
t
ap
t
,
так
что
ap
t
является
актуарной
настоящей
сто
имостью
срочного
аннуитета
с
ежегодными
выплатами
размера
1.
Такая
актуарная
