Бауэрс Н., Гербер Х., Джанс Д., Несбитт С., Хикман Дж. Актуарная математика

Подождите немного. Документ загружается.

21.2.

Сценарии

561

21.1.2.

Обозначения

предварительные

сведения

Символом

мы

будем

обозначать

случайную

величину,

интерпретируемую

как

эффективная

процентная

ставка

на

k-M

расчетном

периоде,

т.

е.

является

од'Но

nерuод7iОЙ

процентной

ставкой

для

этого

k-ro

периода:

капитал

размера

конце

периода

имеет

настоящую

стоимость

1/(1

)

на

начало

периода.

большинстве

приложений,

рассматриваемых

настоящей

главе,

под

расчетным

периодом

будет

пониматься

год

действия

страхового

договора.

большинстве

ранних

исследований

предполагалось,

что

Ik, k =

1,2,

...

имеет

распределение,

сосредоточенное

одной

точке

(называемое

вырожденным),

такое,

что

P(Ik

=i)

= 1, k =

1'2'

....

Из

неравенства

Иенсена

(1.3.3),

котором

u"(х)

О,

может

быть

выведено

одно

непосредственное

следствие

предположения

том,

что

эффективная

(однопе

риодная)

процентная

ставка

является

случайной

величиной.

Переформулируем

это

неравенство

виде

Е[u(Х»)

u(Е[Х).

Если

u(х)

(l+х)-l

иХ

= I

ТО

ull(х)

О,

-1

х,

(21.1.1)

причем

равенство

имеет

место

только

том

случае,

когда

распределение

выро

жденно.

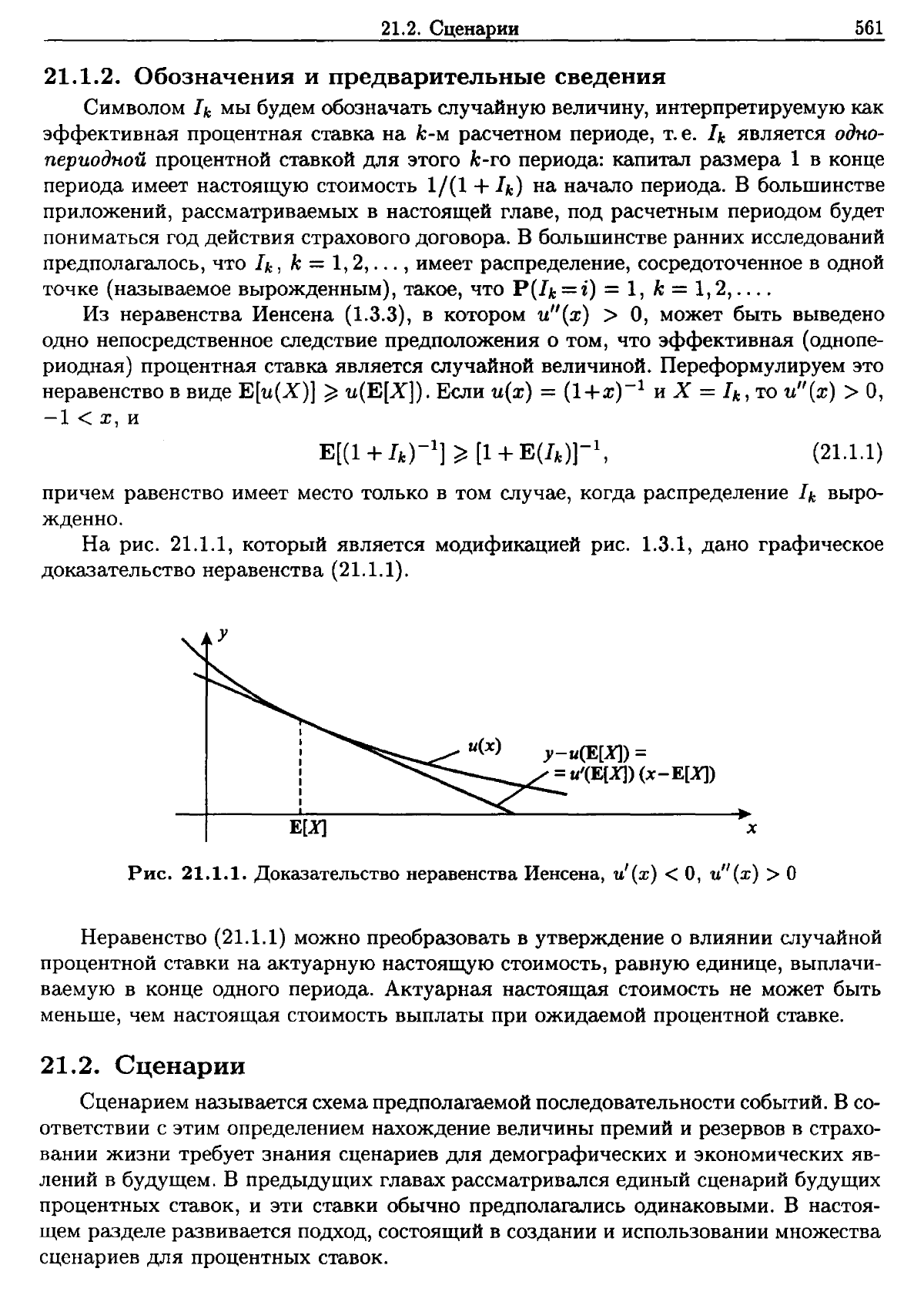
На

рис.

21.1.1,

который

является

модификацией

рис.

1.3.1,

дано

графическое

доказательство

неравенства

(21.1.1).

Е[Х]

y-u(Е[Х])

u'(Е[Х])

(х-

Е[Х])

Рис.

21.1.1.

Доказательство

неравенства

Иенсена,

u'(х)

О,

u"(х)

Неравенство

(21.1.1)

можно

преобразовать

утверждение

влиянии

случайной

процентной

ставки

на

актуарную

настоящую

стоимость,

равную

единице,

выплачи

ваемую

конце

одного

периода.

Актуарная

настоящая

стоимость

не

может

быть

меньше,

чем

настоящая

стоимость

выплаты

при

ожидаемой

процентной

ставке.

21.2.

Сценарии

Сценарием

называется

схема

предполагаемой

последовательности

событий.

со

ответствии

этим

определением

нахождение

величины

премий

резервов

страхо

вании

жизни

требует

знания

сценариев

для

демографических

экономических

яв

лений

будущем.

предыдущих

главах

рассматривался

единый

сценарий

будущих

процентных

ставок,

эти

ставки

обычно

предполагались

одинаковыми.

настоя

щем

разделе

развивается

подход,

состоящий

создании

использовании

множества

сценариев

для

процентных

ставок.

562

Гл.

21.

Проценты

как

случайная

величина

21.2.1.

Детерминистические

сценарии

этой

главе

качестве

детерминистического

сценария

для

процентных

ставок

выбирается

последовательность

iз

...

)

однопериодных

процентных

ставок

на

единичных

периодах

будущем,

которые

определены

актуарием

для

использова

ния

актуарных

расчетах.

качестве

элементов

этой

последовательности

выбраны

наиболее

вероятные,

согласно

представления

актуария

будущей

экономической

ситуации,

значения

процентных

ставок.

Если

актуарий

уверен

величине

будущих

доходов

от

инвестирования,

причем

эта

уверенность проистекает

из

предыдущих

инвестиционных

решений

или

из

специальных

знаний,

то

может

быть

достаточно

одного

сценария.

противном

случае

можно

определить

несколько

сценариев,

что

бы

иметь

возможность

исследовать

чувствительность

актуарных настоящих

стои

мостей

изменениям

экономической

обстановке.

Если

используется

несколько

сценариев,

то

им

приписываются

номера

j = 1,2,

...

,т,

где

m -

количество

сценариев.

Таким

образом,

вектор

(ji

,ji

...

)

обо

значает

сценарий

номер

динамики

процентных

ставок.

Далее,

коэффициенты

дис

контирования

стоимости

аннуитетов,

соответствующие

сценарию

обозначаются

следующим

образом:

)-l

r=l

n-l

jli

LjV

•

k=O

(21.2.1а)

(21.2.1Ь)

Пользуясь

этими

обозначениями

привлекая

материал

из

гл.

4, 5

естественно

определить

= E[;V

]

LjVk+1kPX

Qx+k,

k=O

jli

Еи

К+ll]

jli

kPx Qx+k,

k=O

где

случайная

величина,

определенная

как

число

полных

лет

предстоящей

жизни

лица

возраста

лет.

Применяя

принцип

эквивалентности,

мы

получаем

(21.2.1с)

Символ

стоящий

левой

части

соотношения

(21.2.1с),

не

входит

Меж

дународную

систему

актуарных

обозначений,

его

можно

спутать

символом,

ис

пользованным

гл.

для

обозначения

нетто-премии

по

страхованию

жизни

огра

ниченным

сроком

выплаты

премиЙ.

Несмотря

на

возможную

путаницу,

мы

будем

использовать

этот

символ

настоящей

главе,

чтобы

обеспечить

согласованность

обозначениями,

применяющимися

для

актуарных

настоящих

стоимостей,

вычисля

емых

соответствии

со

сценарием

Определение

дисперсий

для

случайных

величин

потерь,

неявно

входящих

со

отношения

(21.2.1а)-(21.2.1с),

требует

осторожности.

Упрощения,допустимые

слу

чае

постоянной

процентной

ставки,

здесь

неприменимы.

Мы

также

должны

помнить,

что

при

рассматриваемом

сценарии

процентных

ставок

эти

дисперсии

отражают

случайную

природу

только

продолжительности

предстоящей

жизни.

21.2.

Сценарии

Имеем

К+1

] -

(k+1)

q _

(·А

- 2

(.А

J k

х+1

- j

k=O

00 00

D17

K+1a

L(ja

1)2

kPx

qx+k

(ja

=L L

kPx

Qx+k

(за

)2,

k=O

r=O

D17

U =

L(jV

jak+ll)2kPx

Qx+k·

k=O

Пример

21.2.1.

Определяются

четыре

сценария

для

процентных

ставок:

j~l

j~2

j~З j~4

1 0,06 0,06 0,06

0,06

2 0,06

0,03

0,03 0,03

3 0,06

0,09 0,09

0,09

0,06 0,03

0,09 0,03

563

следующей

таблице

дается

дискретное

распределение

пошаговой

продолжи

тельности

предстоящей

жизни

лица

(х):

kPz

q:r;+k

0,1

1 0,2

2 0,3

3 0,4

Подсчитаем

зад

для

j =

1,2,3,4

k =

0,1,2,3

зА

зР

для

J =

1,2,3,4.

Решение.

k=O

k=l

k=2

k=3

k=O

0,9434

0,8900

0,8396 0,7921 1,0000

0,9434

0,9159 0,8892 0,8633

1,0000

3 0,9434 0,8655 0,7940 0,7285 1,0000

4 0,9434 0,9159 0,8403

0,8158 1,0000

k=1

k=2

1,9434 2,8334

1,9434 2,8593

1,9434 2,8089

1,9434 2,8593

k=3

3,6730

3,7486

3,6029

3,6996

jA:r;

ja:r;

jРж

0,8411 2,8079

0,2995

0,8896 2,8459

0,3126

3 0,7970 2,7725

0,2875

0,8559

2,8263 0,3028

Пример

21.2.2.

Воспользовавшись

предположениями

при

мера

21.2.1,

подсчи

таем

JD[;v

+1]

vD17aK+11], j =

1,2,3,4.

(21.2.2a)

21.2.2.

Случайные

сценарии:

детерминированные

процентные

ставки

При

построении

модели

процентных

ставок

будем

считать,

что

актуарий

предло

жил

вероятных

сценариев.

Следующим

шагом

может

стать

определение

распреде

ления

вероятностей

на

множестве

из

этих

сценариев

привлечением

методов,

вы

являющих

индивидуальные

вероятности.

Символом

ри)

обозначается

вероятность

сценария

Это

не

функция

вероятностей

случайной

величины

индивидуальных

страховых

выплат,

как

гл.

12.

Задание

этих

вероятностей

должно

отражать

представление

актуария

вели

чине

будущих

доходов

от

инвестирования.

Процесс

выявления

этих

вероятностей

тесно

связан

процессом

построения

функции

полезности,

который

пояснялся

гл.

Актуарные

настоящие

стоимости

определяются

использованием

совместно

го

распределения

случайной

величины

пошаговой

продолжительности

предстоящей

жизни

сценария

для

процентных

ставок

настоящей

главе

символ

будет

применяться

для

обозначения

случайной

величины,

понимаемой

как

индекс,

припи

санный

сценарию

динамики

процентной

ставки.

Это

не

причина

выбытия,

как

гл.

10.

Будем

предполагать,

что

С.в.

независимы.

Звездочка

нижнем

левом

индексе,

добавленная к

обозначениям

для

актуарных

настоящих

стоимостей,

будет

показывать,

что

математическое

ожидание

берется

относительно

С.в.

.А

EJEKIJ(JvK+l]

EJ(JA

]

LjAxp(j),

j=l

.а

EJEKIJ(JaK+l~

=EJ(Ja

] = L

ри)·

(21.2.2Ь)

j=l

Сохраняя

такое

же

соглашение

для

обозначений

случайной

величины

потерь

пре

мии

для

страхования

на

случай

смерти

постоянной

ежегодной

премией

дискрет

ной

модели,

мы

получаем

L = Jv

.PxJa

Используя

принцип

эквивалент

ности,

приходим

равенству

EJEK1J[L] =

о,

или

.Р

.Ах/.а

дисперсия

с.в.

задается

формулой

21.2.

Сценарии

565

Пример

21.2.3.

Покажем,

что

величину

...

из

формулы

(21.2.2а)

можно

также

определить,

исходя

из

выражения

EKEJIK[JVK+l].

Решение.

силу

предположения

независимости

величина

процентных

ставок

не

влияет

на

распределение

смертности;

EKEJIK[JVK+l]

Ек

[i':,vK+lp(j)]

}=1

[~jvk+lp(j)]

kP. q.+k =

jA.p(j)

.А..

Предположим

теперь,

что

имеется

множество

из

лиц

одинакового

возраста

х,

что

всем

входящим

это

множество

были

предоставлены

одинаковые

договоры

страхования

на

случай

смерти

постоянными

ежегодными

премиями

дискретной

модели

что

С.в.

j =

1,2,

...

пошаговой

продолжительности

предстоящей

жизни

одинаково

распределены.

Кроме

того,

с.в.

, j =

1,2,

...

,n,

С.в.

взаимно

независимы.

Если

нетто-премия

определена

согласно

принципу

эквивалентности,

то

случайная

величина

суммарных

потерь

для множества

из

страхователей

равна

"'(

К·+l

п"

)

JV'

...

гж

+I1

i=l

Дисперсия

величины

суммарных

потерь

задается

выражением

"'D[

K'+l

JV'

-...

i=l

(

п"

)

+n n -

JV -

...

JV -

"'Г

Е[(

К+l

п"

)2]

- n JV -

...

+lI

n(n

1)E[(Jv

...

+11)(JV

...

1)]

nEJEKIJ[(JvK+l

...

JQ.K+ll)2)

n(n

1)EJEKIJ[(JVKl+1

...

JaKl+11)(JVK2+1 -

...

1)]

nD[Jv

...

n(n

[I:(jA.

.Р.

ja.)2

(j)]

;=1

[;

[f~(jVk+l

.Р.

1)2

•

Q.+k

-1)(

А.

.Р.

а.)2

]Р(Л,

566

Гл.

21.

Проценты

как

случайная

величина

Если

нас

интересуют

не

суммарные

потери по

нашему

портфелю

рисков,

состоящему

из

тождественных

страховых

договоров,

средняя

величина

потерь,

то

i?Jv

;+l

.Р

Jii

;+liJ]

К+1

Р"

] ( )

-n'

JaК+Il

+ 1-

~)jAx

.Р

,а

(Л.

(21.2.3)

з=1

При

n ---t

первое

слагаемое

равенстве

(21.2.3)

стремится

нулю,

второе

остает

ся

положительным.

Суммарные

потери

состоят

из

компонент,

причем

эти

компо

ненты

не

являются

независимыми.

При

увеличении

числа

независимых

страховате

лей

этой

более

сложной

модели

со

случайными

сценариями

для

процентных

ставок

отличие

от

случая,

когда

продолжительности

предстоящей

жизни

предполагались

взаимно

независимыми

случайными

величинами,

сценарий

для

процентных

ставок

был

детерминистическим,

дисперсия

средних

потерь

не

стремится

нулю.

этом

можно

убедиться,

заметив,

что

при

единственном

детерминистическом

сценарии

для

процентных

ставок

суммирование

во

втором

слагаемом

равенства

(21.2.3)

дает

нуль.

Тот

факт,

что

на

величину

всех

потерь

влияет

один

тот

же

случайно

выбранный

сценарий

для

процентных

ставок,

признан

одной

из

проблем

управлении

рисками.

Пример

21.2.4.

условиях

примеров

21.2.1

21.2.2

предположим,

что

актуа

рием

сделаны

следующие

вероятностные

заключения

сценариях

для

процентных

ставок:

p(l)

=0,5,

р(2)

=0,2,

р(3)

=0,2

р(4)

= 0,1,

подсчитаем

величины

Рх

.Рх

1]'

Решение.

Воспользовавшись

принципом

эквивалентности,

получим

EJEKIJ[JV

.Р

JaK+11]

О,

.Р

х)р(l)

х)р(2)

(зАх

.рх

х)р(3)

*р

4ах)р(4)

О,

.Р

.А

.а

=0,8435/2,8103 = 0,3001,

D[JV

.Р

= EJEKIJ[(JVK+1 - 0,3001

1)2]

(0,0987)(0,5) + (0,0912)(0,2) + (0,1078)(0,2) + (0,0983)(0,1)

= (0,0990).

21.3.

Независимые

процентные

ставки

разд.

21.2.2

были

введены

случайные

сценарии

для

процентных

ставок.

За

ключения

вероятностях

там

делались

на

основе

экономических

знаний

актуария.

Сейчас

мы

рассмотрим

стохастическую

модель

для

процентных

ставок,

которой

выбор

модели

оценка

параметров

модели

зависят

от

имеющихся

данных.

Пред

положим,

что

актуарий

решил

моделировать

интенсивности

начисления

процента

принял

модель

In(l

+Ik) =

Ck,

k =

1,2,3,

...

, (21.3.1)

где

неотрицательная

постоянная

Ck -

независимые

одинаково

распределен

ные

случайные

величины

распределением

N(O,

(72).

Эта

модель

может

рассматри

ваться

как

модель

долгосрочной

средней

интенсивности

начисления

процента

при

21.3.

Независимые

процентные

ставки

567

наличии

случайных

возмущений.

силу

предположений

относительно

распределе

ния

слагаемых,

ответственных

за

эти

случайные

возмущения,

возможны

отрица

тельные

интенсивности

начисления

процента.

Некоторые

актуарии считают

из-за

этого

модель,

определенную

формулой

(21.3.1),

несостоятельноЙ.

Другие

принима

ют

ее,

поскольку

моделировать

интенсивность

начисления

процента

кажется

есте

ственным,

отрицательные

значения

наблюдаются

инвестиционных

операциях.

Итак,

С.в.

ln(1 +Ik)

имеют

одинаковое

распределение

N(O,

0-2),

с.в.

1 +

имеют

логнормальные

распределения.

Логнормальное

распределение

было

введено

табл.

14.2.1

как

одно

из

распре

делений

величины

страховых

выплат.

Напомним,

что,

согласно этой

таблице,

Логарифмом

случайной

величины,

которая

соответствует

детерминированной

накопленной

процентной

ставке

+i)n,

является

случайная

величина

n n

+Ik) = Lln(1+1

k),

k=l

Согласно

равенствам

(21.3.1),

она

имеет

распределение

N(no,

n0"2).

Поэтому

функ

ция

накопленных

процентов

имеет

логнормальное

распределение

Полезно

заметить,

что

если

0"2 =

О,

то

математическое

ожидание

накопленных

про

центов

равно

дисперсия

этой

случайной

величины

равна

нулю.

Логарифм

коэффициента

дисконтирования

ln(1 +

Ik)-l

-ln(1

+Ik) =

-о

f:k

имеет

распределение

-о,

(

Ik)-l

логнормальное

распределение

Е[(1

Ik)-l]

e-(6-u

j2)

О,

D[(1 +

Ik)-l]

(е

и2

1)(е-

и2

)

О.

Определим

функцию

дисконтирования

как

случайную

величину

Ik)-l,

k=l

Выбор

символа

мотивирован

использованием

символа

для

обозначения

коэф

фициента

дисконтирования

разд.

4.3.

Волна

над

символом

указывает

на

то,

что

является

случайной

величиной.

Далее,

С.в.

lnV

= -

2:Z=lln(1

+ Ik)

имеет

рас

пределение

-по,

логнормальное

распределение

математическим

ожиданием

E[v

]

(iS-u

j2)

дисперсией

D[v

]

(е

nи2

1)е

(-26+и

(21.3.2)

снова,

если

0"2 =

О,

мы

приходи

ранее

излагаВ1llимся

детерминистическом

случае

результатам.

Мы

предположим,

что

С.в.

, k =

1,2,3,

...

С.в.

К,

пошаговая

продолжи

тельность

предстоящей

жизни,

взаимно

независимы,

рассмотрим

более

сложные

568

Гл.

21.

Проценты

как

случаАная

величина

актуарные

модели.

Актуарная

настоящая

стоимость

страхования

жизни

выплатой

размера

единица

равна

(21.3.3)

.А

=E[VK+l) =

EvE

Iv[VK+l)

[

]

-(б-u

j2)(k+l)

Vk+l

kPx

qx+k

kPx

qx+k·

k=O

Актуарная

настоящая

стоимость

.А

вычисляется

при

детерминированной

интен

сивности

начисления

процента

/2.

Для

того

чтобы

измерить

риск,

положим

D[VK+l) =E[(VK+l)2) -

(.А

EvE

Iv[(VK+l)2)

(.А

Е;;

[~(Vk+l)2kPX

QX+k]

(.А

)2,

Поскольку

С.В.

Vk+l

имеет

логнормальное

распределение

параметрами

-(k

l)б

(k+

1)а

мы

можем

вычислить

E[(Vk+l)2),

второй

центральный

момент,

следующим

образом:

E[(Vk+l)2] = D[Vk+l] +(E[Vk+l])2 =

(e(k+l)U

1)е(k+l)(-2б+u

)

е-

(k+l)(б-

2j2)

= e-(k+l)[2(o-u

)]

, (21.3.4)

К-l

а.

Юii

= L V

;

8=0

поэтому

- ] -

"'е-(k+l)[2(б-u

)]

q _ (

К+l

L..J

x+k

•

k=O

Можно

видеть,

что

при

мы

приходи

результатам

гл.

Выражения

для

актуарных

настоящих

стоимостей

аннуитетов

требуют

б6льших

вычислений,

процессе

которых

мы

по-прежнему

будем

предполагать,

что

С.в.

k =

1,2,

...

взаимно

независимы.

Положим

тогда

.ах

E[Q,K+llii)

EKE

[Q,K+llii)

Ек[а.К+llб-u2j2)

L(а.

Iб-u

j2)

kPx

Qx+k·

k=O

(21.3.5)

Чтобы

вычислить

D[aK+1I

начнем

соотношений

Е;;

[(

v.)

=E;;[(l +

+'"

Vk)2]

Е;;

[~(V.)2

~rtl

V.Vr]

k-l

е-

[2(б-u

)]

+2L L E[v

8=0

8=ОТ=8+1

Выражения

вида

E[(v

)2]

были

вычислены

применением

соотношения

(21.3.4).

21.3.

Независимые

процентные

ставки

Рассмотрим

выражения

под

знаком

двойного

суммирования

при

s <

т:

E[vsv

] =

Е[(1

+11)-2

...

)-2(1

+18+1)-1

...

)-1]

-s[2(б-

2»)-(r-s)(6-

2j2)

-е

569

(21.3.6)

Для

вывода

формулы

(21.3.6)

использовались

независимость

с.в.

1k, k = 1,2,

...

соотношения

(21.3.2)

(21.3.4).

Итак,

мы

получаем

(21.3.7)

Двойное

суммирование

равенстве

(21.3.7)

можно

упростить,

изменяя

порядок

сум

мирования

при

меняя

формулу

суммирования

геометрической

прогрессии.

Мы

по

лучаем

(21.3.8)

(21.3.9)

Заметим,

что

суммирование

формуле

(21.3.8)

может

начинаться

r =

О,

поскольку

соответствующее

слагаемое

равно

нулю.

Объединяя

промежуточные

результаты

формул

(21.3.7)

(21.3.8),

мы

получаем

D[a

+llii]

Ек

EiiIK[(aK+llii)2] -

(.а

[

-8[2(о-и2»)

(6-

2j2) _

е-

[26-

2и

2]]

Ек

L-i

1 _

e-[o-(3

2j2»)

а=О

т=О

а"

+ 2

.а

аж

(

ах

1 _

е-[б-(3u2j2)]

.а

где

величина

Qii

вычислена

при

интенсивности

начисления

процента,

равной

2(8 -

0-2).

Если

О,

то

соотношение

(21.3.9)

приобретает

вид

2а

2(а

- 2

)/d

(а

)2,

где

величина

ах

вычислена

при

интенсивности

начисления

процента

28,

ах

при

интенсивности

начисления

процента

Этот

результат

можно

сравнить

формулой

(5.3.8),

где

1 - (2d - d

)

- 1+

2da"",

да":

_----=-

----=-

'"'

а_-=-'"'

_ 2

+а

ах

_("

)2.

ах

ах,

это

еще

раз

показывает,

что

при

0-2 =

мы

приходи

результатам,

получавшимся

для

детерминированных

процентных

ставок.

Пример

21.3.1.

Предположим,

что

lп(1

+ 1

)

= 8 +

ck,

k =

1,2,3,

...

где

8 = 0,06

слагаемое,

ответственное

за

случайные

возмущения,

имеет

распределе

ние

N(O, 0,0001).

Случайная

величина

пошаговой

продолжительности

предстоящей

жизни

имеет

дискретное

распределение,

показанное

примере

21.2.1.

Вычислим

(а)

E[VK+l]'

(Ь)

D[VK+l],

(с)

E[aK+1I

]

(d) D[iiK+1I

Мы

будем

предполагать,

что

С.в.

1k, k =

1,2,3,

...

независимы.

570

Гл.

21.

Проценты

как

случайная

величина

Решение.

(а)

Согласно

(21.3.3),

- ] -

e-(О,О6-0,ОООО5)(k+l)

К+l

ж+k

k=O

=(0,9418)(0,1) + (0,8870)(0,2) + (0,8354)(0,3) + (0,7868)(0,4) =0,8369.

(Ь)

Согласно

(21.3.4),

D[VK+l] =L

e-(2(О,О6-0,ООООl)](k+l)

kРж

qж+k

(.А

k=O

= (0,8871)(0,1) + (0,7869)(0,2) + (0,6981)(0,3) + (0,6193)(0,4) - (0,8369)2

=0,0028.

(с)

Получаем

[а

] -

(О,О6-0,ОООО5)

K+ll1i

ж+k

k=Os=O

= (1)(0,1) + (1,9418)(0,2) + (2,8288)(0,3) + (3,6642)(0,4) = 2,8027.

(d)

Вычисление величины

D[a

Iv]

начинается

величины

Qо.ж,

рассчитанной

при

интенсивности

начисления

процента

2(8 -

0'2)

= 0,1198:

Qii

= (1)(0,1) + (1,8871)(0,2) + (2,6740)(0,3) + (3,3721)(0,4) =2,6285,

и,

согласно

(21.3.9),

[

..]

2,8027 - 2,6285 ( 2

D a

=2,6285 + 2 1 _

е-

,О5985

- 2,8027) = 8,6257 - 7,8551 =0,7705. "

Пример

21.3.2.

Примем

предположения

распределении

величин

ln(l

+Ik)

К,

сформулированные

примере

21.3.1.

Найдем

функцию

распределения

С.В.

'йК+l'

Решение.

P(VK+l

у)

EKP(VK+l

=LP(Vk+l

У)

kРж

qж+k·

k=O

Воспользуемся

теперь

тем,

что

P(VK+l

~y)

LP(lnVk+l

lПУ)kржqж+k

k=O

[ln

Vk+l

+(k + 1)8

+ (k + 1)8]

J(k

1)0-2

J(k

1)0-2

kРж

qж+k

[ln

(k +

1)8]

[ln

+(k +1)(0,06)]

J(k

1)0'2

kРж

qж+k

J(k

+ 1)(0,01)

kРж

qж+k,

где

Ф(w)

является

функцией

распределения

случайной

величины

распределени

ем

N(O, 1).

качестве

при

мера

положим

= E[VK+l] =

.А

=0,8369

вычислим

P(VK+l

0,8369) =

Ф(

-11,8051)(0,1)+Ф(

-4,1048)(0,2)+Ф(0,1125)(0,З)+Ф(3,D945)(0,4)