Бауэрс Н., Гербер Х., Джанс Д., Несбитт С., Хикман Дж. Актуарная математика
Подождите немного. Документ загружается.


21.4.
Зависимые
процентные
ставки
571
= 0,5630.
Так
как
медиана
с.в.
VK+l
меньше
ее
среднего,
это
свидетельство
того,
что
ее
распределение
асимметрично
с
большей
массой
левее
среднего.
"
21.4.
Зависимые
процентные
ставки
В
финансовой
экономике
ведутся
продолжительные
дискуссии
о
том,
можно
ли
применять
независимые
и
одинаково
распределенные
случайные
величины
для
моделирования
эффективных
процентных
ставок
в
различных
классах
инвестиро
вания.
В
том
случае,
когда
актуарий
считает
достаточными
свидетельства
в
пользу
гипотезы
о
независимости
и
одинаковой
распределенности,
можно
при
менять
мето
ДЫ,
развитые
в
разд.
21.3.
Актуарий
может
вносить
в
эти
методы
изменения.
Напри
мер,
в
качестве
распределения
случайных
величин
ek,
слагаемых,
ответственных
за
случайные
возмущения,
не
обязательно
брать
распределение
N(O,
0'2).
Если
актуарий
отвергает
гипотезу,
что
эффективные
процентные
ставки
явля
ются
независимыми
и
одинаково
распределенными
случайными
величинами,
то
воз
никают
две
возможности.
Первая
состоит
в
том,
чтобы
разработать
многомерную
модель,
которая
не
меняется
с
течением
времени.
Такие
модели
называются
стаци
онарными.
Простая
модель
из этого
класса
будет
предложена
в
разд.
21.4.1.
Вторая
возможность
-
применить
модель,
в
которой
учитывается
возможность
структурных
сдвигов
в
инвестиционном
окружении.
Такие
модели
мы
обсуждать
не
будем.
21.4.1.
Модель
скользящего
среднего
В
настоящем
разделе
мы
ограничиваемся
моделью
k =
1,2,3,
...
, (21.4.1)
где
д
>
О
и
ck,
k =
1,2,3,
...
,
являются
взаимно
независимыми
случайными
вели
чинами,
каждая
из
которых
имеет
распределение
N(O,
0'2).
Кроме
того,
IBI
~
1
и
ео
известно.
Если
В
=
О,
эта
модель
превращается
в
модель
(21.3.1).
Она
называ
ется
моделью
С1Солъзящего
среднего
первого
nоряд1Са,
или,
пользуясь
сокращением,
МА(l).
Смысл
этой
модели
состоит
в
том,
что
интенсивность
начисления
процента
име
ет
долгосрочное
среднее
значение
д,
но
случайные
экономические
возмущения
по
рождают
отклонения
от
этого
среднего.
Возмущение
ek,
отвечающее
периоду
с
но
мером
k,
оказывает
отсроченное
и
уменьшенное
влияние
размера
-Bek
на
интен
сивность
начисления
процента
в
интервале
с
номером
k +1.
Мы
определим
V
N
так же,
как
в
разд.
21.3:
n
V
n
=
П
(1
+
Ik)-l
=
е-
E~
(6+e",-Oele-l)
j
k=l
тогда
n
n-l
ln v
n
=-
L(д
+
ek
- Bek-l) =
-nд
+
сп
-
Вео
+
(1
-
В)
L
ek
k=l
k=l
и
E[v
n
]
=
Е(е-[n6+е
n
-Oeo+(l-O}
E~~;
ele]).
Мы
предположили,
что
с.в.
ck,
k = 1,2,
...
,
n,
взаимно
независимы
и
каждая
из
них
имеет
распределение
N(O,
0'2).
Поэтому,
вспоминая
вид
производящей
функции
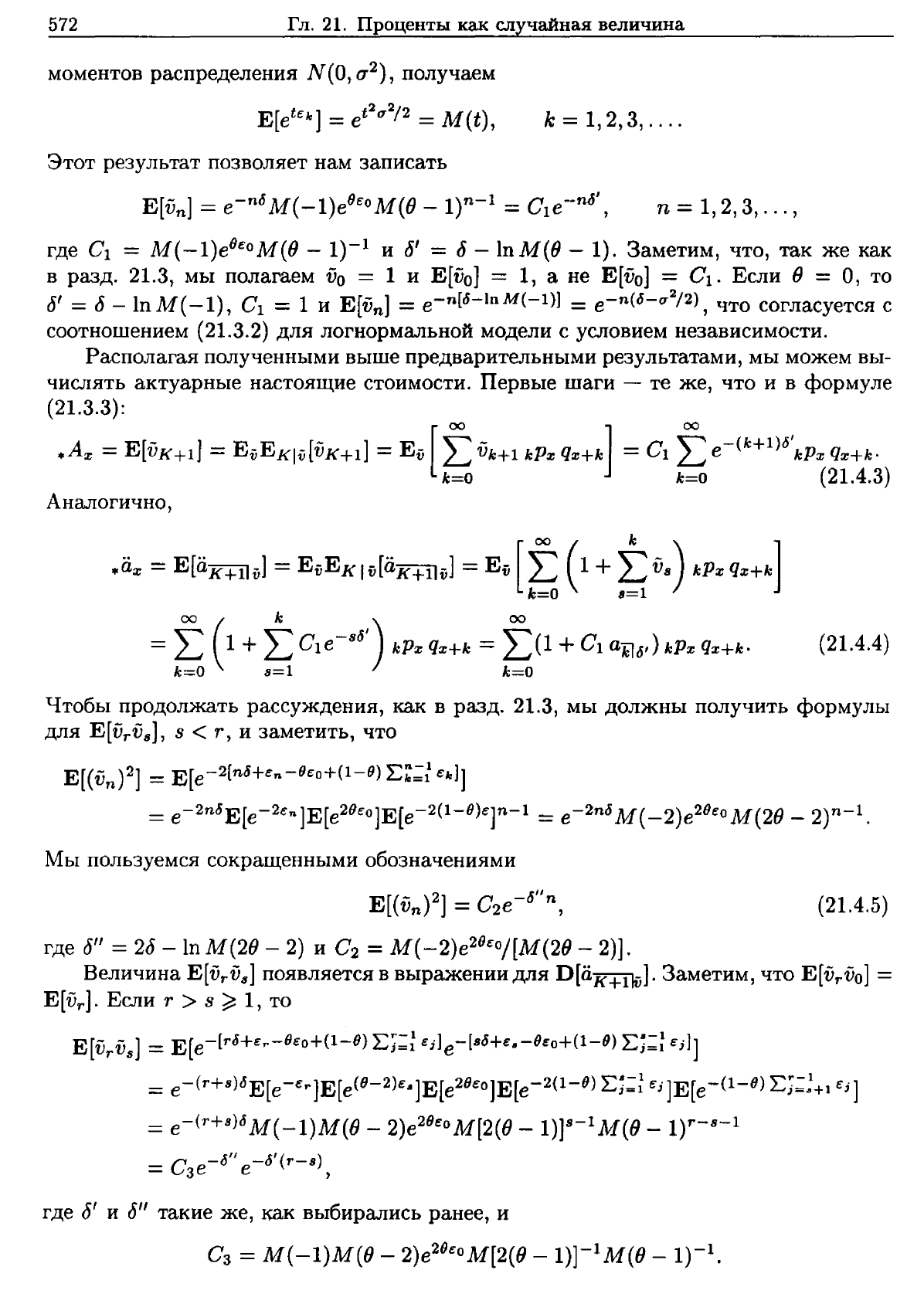
572
Гл.
21.
Проценты
как
случайная
величина
моментов
распределения
N(O,
(72),
получаем
E[ete:
k
]
=et2q2/2 =
M(t),
k =
1,2,3,
....
(21.4.4)
(21.4.5)
Этот
результат
позволяет
нам
записать
E[v
n
]=
е-ПО
М(
_1)е
8
е:
о
М(В
-
1)n-l
=
C
1
e-
nО
',
n =
1,2,3,
...
,
где
С
1
=
М(-1)е
8
е:
о
м(в
- 1)-1
и
д'
=
д
-lпМ(В
- 1).
Заметим,
что,
так
же
как
в
разд.
21.3,
мы
полагаем
-ио
= 1
и
E[vo]
= 1,
а
не
Е
[vo]
=
С
1
•
Если
В
=
О,
то
д'
=
д
-lпМ(-l),
С
1
= 1
и
E[v
n
]
=
e-
п
[о-lпМ(-I}]
=
e-
n
(O-q2/
2
) ,
что
согласуется
с
соотношением
(21.3.2)
для
логнормальной
модели
с
условием
независимости.
Располагая
полученными
выше
предварительными
результатами,
мы
можем
вы
числять
актуарные
настоящие
стоимости.
Первые
шаги
-
те
же,
что
и
в
формуле
(21.3.3):
А
-
Е[-
J -
Е-Е
[- ] -
Е
[~-
] -
С
~
-(k+l}o'
*
х
-
VK+l
- v
Klii
VK+l
-
ii
L..J
Vk+l
kPx
Qx+k
- 1
L..J
е
kPx
Qx+k·
k=O
k=O
(21.4.3)
Аналогично,
.а.
=E[aK+Hii] =EiiE
K
Iii[aK+,Jii] =
Е
;;
[
f:
(1
+ t
ii.)
kP. q.+k]
k=o
8=1
00
(k
)
00
=
{;
1+
~
с,е-·
6
'
kP.
q.+k =
{;(l
+
С,
aJil6')
kP.
q.+k.
Чтобы
продолжать
рассуждения,
как
в
разд.
21.3,
мы
должны
получить
формулы
для
E[vrv
s
],
s <
r,
и
заметить,
что
E[(V
n
)2]
=
Е[е-2[nб+е:n-Ое:о+(1-О)
Е:::
E:k]]
=
e-2nОЕ[е-2е:n
]E[e
20
e:
O
]E[e-
2
(1-8)е:]n-1
=
е-
2nо
М(
_2)е
2О
Е:О
М(2В
_
2)n-l.
Мы
пользуемся
сокращенными
обозначениями
Е[(
-
)2]
С
-6//n
V
N
=
2
е
,
где
611
=
2д
-ln
М(2В
-
2)
и
С
2
=
М(
-2)е
2О
е:
о
j[М(2В
- 2)J.
Величина
E[vrv
s
]
появляется
в
выражении
для
D[ii
к
+
1ю
].
Заметим,
что
E[vrvo]
=
E[v
r
].
Если
r > s
~
1,
то
E[vrv
s
]=
Е[е-[rб+е:
..
-Ое:о+(1-0)
Ej::
E:i]e-[sб+Е
8
-ОЕо+(1-8)
'2:;::
Ej]]
=
e-(r+s)БЕ[е-
Еr
]E[eUJ-2)Е8
]E[e28EO]E[e-2(1-0)
'2:;::
Е;
]Е[е-(1-0}
'2:j:~+1
E:j]
=
е-(r+s)б
М(
-1)M(B
-
2)е
28
Е:О
М[2(В
-
1)]В-1
М(В
_
1?-в-1
_
С
-0//
-о/
(т-в)
-
зе
е
,
где
д'
и
д"
такие
же,
~K
выбирались
ранее,
и
С
З
=
М(
-l)М(В
-
2)е
2ОЕО
М[2(В
- 1)]-1
М(В
- 1)-1.

21.4.
Зависимые
процентные
ставки
573
Используя
эти
результаты,
мы
выводим
формулу
для
дисперсии
случайных
величин
настоящих
стоимостей
в
модели,
где
интенсивность
начисления
процента
подчиня
ется
модели
МА(l):
00
D[VK+l] =E[(VK+l)2] -
(.А
х
)2
=
L:
C
2
e-<5"(k+l)
kPx
Qx+k
-
(.А
х
)2.
k=O
При
выведении
этих
равенств
мы
использовали
формулы
(21.4.3)
и
(21.4.5).
Для
нахождения
величины
D[a
K
+lIv]
начнем
с
формулы
(21.4.6)
(21.4.8)
E
v
[(t
v.)2]
= E
v
[(1+
t
v;)
+2
~
t
vrv.]
8=0
а=1
s=Or=s+1
k k
k-l
k
=
(1
+
L:
С
2
е-
б
"
а)
+2
(L:
С
2
е-
rб
'
+
L: L:
Сзе-б"s-б'
(r-s)).
а=1
r=1
а=1
т=а+1
(21.4.7)
Таким
образом,
D[a
K
+
1
1;;]
=
f:
Е;;
[
(1
+t
v.)
2]
kPz
Qz+k
-
(.а
х
)2,
k=O
8=1
а
выражения
для
слагаемых
в
правой
части
даются
формулами
(21.4.7)
и
(21.4.4).
Пример
21.4.1.
Предположим,
что
выражение
In(l
+Ik)
определяется
форму
лой
(21.4.1)
при
8 = 0,06, D[ekJ = 0,0001,
О
=
-0,8
и
Е:О
=
О.
Определим
(а)
8',
(Ь)
С
1
,
(с)
8", (d)
С
2
и
(е)
С
з
.
Решение.
(а)
8' =8
-ln
М«()
-
1)
=0,06
_ln(e(-0,S-I)2(0,OOOOI)/2)
=0,05984.
(Ь)
С
1
=
~«/~e~;o
=
e(o,OOOOl)j2
e
-(l,8)'(О,ООООl)j2
=0,99989.
(с)
8" =
28
-lпМ[2(О
-
1)]
=0,12
_ln(e[2(-1,8)]2(O,OOOOI)/2)
= 0,119352.
М(
_2)e28~o
е(-2)2(0,ООООI)/2
(d)
С
2
=
М(20
_
2)
=
е(-З,6)2(О,ООООI)/2
=0,99955.
М(
-l)М(О
-
2)е
28ео
e(o,OOOOI)/2
e
(-2,8)2(о,ООООI)/2
(е)
С
З
=
М(20
_
2)М(О
_
1)
=
е(-З,6)2(О,ООООI)/2
е
(-1,8)2(О,ООООl)/2
=0,99963.
~
При
мер
21.4.2.
В
модели
процентных
ставок
из
при
мера
21.4.1
для
функции
дожития
из
примера
21.2.1
определим
(а)
E[VK+l]'
(Ь)
D[VK+l]'
(с)
E[a
K
+
1
Iii]
и
(d) D[a
K
+
1
Iv]'
Решение.
(а)
Согласно
(21.3.4),
E[VK+l] =
EKE
ii
I
K
[VK+IJ
00
з
=
L:
С
1
е-(k+l)б'
kPx
Qx+k
= (0,99989)
L:
С
1
e-(k+l)(О,О5984)
kPx
Qx+k
k=O
k=O
= (0,99989)[(0,94192)(0,1) +(0,88720)(0,2) +(0,83567)(0,3) +
(О,78713)(О,4)]
=0,83710.

574
Гл.
21.
Проценты
как
случайная
величина
(Ь)
Согласно
(21.4.6),
3
-
~
-6"(k+l}
2
D[VK+IJ
=
L...J
С
2
е
kРж
qж+k
-
(*А
ж
)
k=O
= (0,99955)[(0,88721)(0,1) + (0,78714)(0,2)
+(0,69836)(0,3) +(0,61959)(0,4)] - (0,83710)2 = 0,0024.
(с)
Получаем
E[ii
K
+
1
Iv]
=EiiE
K
Iv[iiK+llii] =
[~
(1
+
f:
С
1
е-
В5
')
kРж
qж+k
=(1)(0,1) +(1,94181)(0,2) +(2,82892)(0,3) +(3,66450)(0,4) =2,80284
(d)
Воспользовавшись
формулой
(21.4.7),
вычислим
сначала
Eii[(l
+
2::=1
V
s
)2]
для
k =
О,
1,
2,
3.
Эти
вычисления
сведены
в
следующую
таблицу:
о
1
1
[1
+
С
2
е-
6
"
+
2Сlе-6']
2
[1
+
C2(e-
БJl
+
е-
26
")
+
2(С
1
е-
б
'
+
Сlе-
26
'
+
С
з
е-
6
"-6')]
3
[1
+
С2(е-
б
"
+
е-
26
"
+
е-
36
")
+
2(Сl
е
-
6
'
+
е-
26
'
+
е-
36
')
+Сз(е-
6
"-6'
+
е-
6
"-26')
+
С
з
(е-
26
"-б
ll
)]
=1
= 3,77043
= 8,00214
=13,42729
D[aK+lliiJ = (1)(0,1) + (3,77043)(0,2) + (8,00214)(0,3) + (13,42729)(0,4) - (2,80284)2
= 0,7699.
~
21.4.2.
Реализация
В
разд.
21.3
и
21.4.1
показано,
что
если
процентные
ставки
предполагаются
слу
чайными
величинами,
то
вывод
формул
для
моментов
случайных
величин
насто
ящих
стоимостей
может
состоять
из
нескольких
этапов.
Аналогичные
шаги
могут
применяться
к
другим
статистическим
моделям
для
X
k
= ln(1 +
[k),
принадлежа
щим
к
тому
же
классу
моделей,
а
именно,
к
(а)
авторегрессионной
модели
первого
порядка
AR(1),
(Ь)
AR(I)
и
МА(I),
(X
k
-
б)
-
Ф(Хk-l
-
б)
=
Ck
- (}Ck-l,
(с)
AR(I)
для
первых
разностей,
(Xk -
Xk-l)
-
Ф(Х
k
-
1
-
Xk-2)
= ck·
(21.4.9а)
(21.4.9Ь)
(21.4.9с)
Выбор
подходящей
модели
для
интенсивности
начисления
процента
и
оценка
входя
щих
в
нее
параметров
относится
к
области
статистики.
Мы
не
касались
важной
задачи
нахождения
функции
распределения
случай
ных
величин
настоящих
стоимостей.
Техника,
использованная
в разд.
4.2, 5.2, 6.2
и
7.2,
не
годится
для
случая,
когда
с.в.
К
и
С.В.
Vk,
пошаговая
продолжительность

21.4.
Зависимые
процентные
ставки
575
предстоящей
жизни
и
коэффициенты
дисконтирования,
зависимы
и
заданы
своим
совместным
распределением.
В
предыдущих
главах,
в
которых
случайными
были
только
пошаговые
продол
жительности
предстоящей
жизни,
предлагались
аппроксимации
для
распределения
потерь
по
портфелю
рисков.
При
этом
мы
предполагали,
что
случайные
величины
продолжительности
предстоящей
жизни
взаимно
независимы.
Обычно
такие
рассу
ждения
используют
результат
типа
центральной
предельной
теоремы,
который
об
основывает
использование
аппроксимирующих
нормальных
распределений.
В
слу
чае
когда
каждая
компонента
случайных
величин
настоящих
стоимостей
является
функцией
одного
и
того
же
процесса
процентных
ставок,
эти
случайные
величины
более
не
являются
независимыми,
что
иллюстрируется
соотношением
(21.2.3).
Та
ким
образом,
когда
процентные
ставки
также
являются
случайными
величинами,
распределение
суммарных
потерь
по
портфелю
случайных
величин
настоящих
сто
имостей
не
может
быть,
как обычно,
приближено
с
использованием
нормального
распределения.
К
трем
задачам
для
портфеля
страховых
рисков,
оценке
моментов
случайных
величин
настоящей
стоимости,
аппроксимации
функции
распределения
настоящей
стоимости,
аппроксимации
функции
распределения
настоящей
стоимости
потерь,
имеются
подходы,
основанные
на
имитационном
моделировании.
Опираясь
на
реа
лизации
значений
случайной
величины
с
распределением
N(O,
(2),
можно
генериро
вать
выборочные
траектории
(11,12,
...
)
для
таких
моделей,
как
в
(21.3.1), (21.4.1)
и
(21.4.6
а,
Ь
и
с).
Если
{l
k
},
последовательность
будущих
эффективных
процентных
ставок,
и
К,
полное
число
лет
предстоящей
жизни,
предполагаются
независимыми,
то
стандартными
методами
можно
построить
эмпирическую
функцию
распределе
ния,
которая
приближает
функцию
распределения
случайной
величины
индивиду
альных
потерь.
В
качестве
примера
рассмотрим
ситуацию,
когда
с
помощью
модели
МА(l),
опи
санной
соотношением
(21.4.1),
генерируются
100
последовательностей
величин
бу
дущих
процентных
ставок.
Для
каждой
ИЗ
этих
последовательностей
с
применением
некоторой
заранее
заданной
функции
дожития
будет
определяться
реализация
слу
чайной
величины
К
полного
числа
лет
предстоящей
жизни.
На
основе
этих
резуль
татов
можно
подсчитать
100
выборочных
значений
С.в.
VK+l.
Эти
значения
можно
рассматривать
как
выборку,
полученную
из
совместного
распределения
С.в.
{l
k
}
и
К.
Среднее
и
дисперсия
этих
100
выборочных
значений,
полученных
имитацион
ным
методом,
будут
оценками
среднего
и
дисперсии
распределения
С.в.
VK+l.
Эмпи
рическая
функция
распределения
будет
оценкой
функции
распределения
с.в.
VK+l'
Процедура
имитационного
моделирования
может
также
применяться
для
при
ближения
функции
распределения
настоящей
стоимости
суммарных
потерь
по
порт
фелю,
состоящему
из
n
индивидуальных
рисков.
В
этом
случае
существует
множе
ство
случайных
величин
числа
полных
лет
предстоящей
жизни
K
i
,
i =
1,2,
...
,n.
Если
эти
случайные
величины
предполагаются
независимыми,
то
для
имитации
зна
чений
случайной
величины
настоящей
стоимости
суммарных
потерь
используется
имитация
значений
каждой
С.в.
K
i
И
случайным
образом
генерированный
сценарий
динамики
процентных
ставок.
Понятно,
почему
имитационное
моделирование
с
использованием
полученных
на
компьютере
реализаций
случайных
величин
настоящих
стоимостей,
которые
мо
гут
быть
функциями
нескольких
случайных
величин,
широко
используется
для
по-

576
Гл.
21.
проценты
как
случайная
величина
строения
эмпирических
функций
распределения.
Описанные
приложения
вывели
имитационное
моделирование
в
ряд
важных
методов
актуарной
науки.
Если
имеются
свидетельства,
что
случайные
величины
времени до
выбытия
и
причины
выбытия
не
являются
независимыми
от
С.в.
{Ik},
то
построение
реализаций
случайных
величин
настоящих
стоимостей
становится
более
сложным.
Например,
факт
и
время
расторжения
договора
страхования
или
выхода
из
пенеионной
схемы
могут
зависеть
от
С.в.
{I
k
}.
21.5.
Модели
финансовой
экономики
На
основе
данных
об
инвестиционных
операциях
моделируемой
финансовой
си
стемы
можно
выбрать
одну
из
моделей,
описанных
в
разд.
21.3
и
21.4,
и
оценить
па
раметры
этой
модели.
Критически
настроенные
специалисты утверждают,
что
эта
процедура
не
принимает
во
внимание
важную
информацию,
имеющуюся
на
рынках
капитала.
Для
того
чтобы
продемонстрировать
изменчивость
с
течением
времени
доходно
сти
при погашении
одной
из
разновидностей
ценных
бумаг,
на
рис.
21.1.1
показана
средняя
доходность
при
погашении
для
30-летних
облигаций
Казначейства
США.
Изменения
цены
и
доходности
облигаций
отражают
изменения оценки
рынком
об
лигаций
будущих
экономических
событий.
Конечно,
имеется
много
других
видов
инвестиций,
которые
могут
отражать
различные
схемы
доходности
за
тот
же
самый
период
времени.
Экономические
новости
влияют
на
доходность
различных
ценных
бумаг
по-разному.
Даже
облигациям
Казначейства
с
различными
сроками
погаше
ния
могут
отвечать
различные
BpeMeHHbIe
ряды
уровней
доходности.
21.5.1.
Информация
о
ценах
и
сроках
погашения
Для
того
чтобы
получить
информацию
о
взаимосвязи
между
процентными
став
ками
и
сроками
погашения,
освобожденную
от
таких
усложняющих
картину
факто
ров,
как
риск
отказа
от
уплаты
и
риск досрочного
погашения
(досрочного
погашения
по
желанию
заемщика),
обычно
анализируют
облигации,
выпущенные
центральны
ми
правительствами.
В
Соединенных
Штатах
Америки
это
-
облигации
Казначей
ства.
Анализ
прочих
облигаций
проводится
путем
их
сравнения
с
облигациями
Каз
начейства.
Чтобы
проиллюстрировать
методы,
используемые
для
оценки
взаимосвязей
меж
ду
процептными
ставками
и
сроками
погашения,
требуется
обратиться к
основным
положениям
финансовой
математики.
Рассмотрим
'Чuстую
дUС7Сонтную
обл.uгацuю,
по
которой
выплачивается
одна
единица
в
момент
погашения
и
которая
продается
па
рынке
без
оплаты
расходов
на
совершение
сделки.
Эти
облигации
не
подвержены
риску
отказа
от
уплаты.
Через
s
обозначается
текущее
время,
и
имеются
дисконт
ные
облигации
со
сроками
погашения
s, s +1, .
..
.
Цена
одной
облигации
в
момент
времени
s,
до
погашения
которой
остается
t BpeMeHHbIx
периодов,
обозначается
че
рез
P(s, s +
t).
Предположим,
что
P(s, s) = 1,
Нт
P(s,t) =
О
и
P(s, t) > P{s,
и)
при
и
>
t.
t-+oo
Третье
предположение
эквивалентно
тому,
что
более
ранней
из
двух
равных
по
ве
личине
выплат
отвечает
б6льшая
стоимость.
Уровень
доходности
за
t BpeMeHHbIx
периодов
обозначается
через
i(s,s +t)
и
определяется
соотношением
P(s, s +t) =
[1
+i(s, s +t)]-t. (21.5.1)

21.5.
Модели
финансовой
экономики
577
Число
i(s,
s +t)
называется
став1СОЙ
«спот»
на
t
периодов
в
момент
времени
s.
Та
кие
ставки
могут
быть
определены
по
текущему
состоянию
рынка
и
связаны
с
еди
новременной
выплатой
в
определенный
момент
в
будущем.
Ставки
«спот»
i(s, s+t),
рассматриваемые
как
функции
от
t,
называются
временной
стРУ1Стурой
процент
ных
ставок
в
момент
времени
s.
Форвард'Н'Ые
ставки
-
другой
подход
к
изучению
взаимосвязи
между
временем
до
погашения
и
процентными
ставками.
Форвардные
ставки
являются
процентны
ми
ставками,
которые
следует
применять
к
договорам,
заключающимся
в
настоя
щий
момент
и
предусматривающим
оплату
в
будущем.
Требуется,
чтобы
эти ставки
были
согласованы
с
множеством
ставок
«спот»,
наблюдаемых
на
рынке
в
текущий
момент.
Эта
согласованность
заключается
в
отсутствu:u.
возможности
арбитра
жа
в
форвардных
ставках.
Возможность
арбитража
возникает
на
рынке
капитала
тогда,
когда
для
одного
и
того
же
инвестиционного
периода
имеются
две
страте
гии
инвестирования,
такие,
что
одна
из
них
заведомо
будет
приводить
к
большему
капиталу
в
конце
периода,
чем
другая.
Для
иллюстрации
требования
отсутствия
возможности
арбитража
предположим,
что
инвестор
выплачивает
сумму
размера
1
за
дисконтную
облигацию
со
сроком
погашения
s +
и
и
стоимостью
при
погашении
[1
+i(s, s +
u)]и.
Действуя
иначе,
инвестор
мог
бы
приобрести
облигацию
со
сроком
действия
t (t <
и)
и
в
момент
t +s
инвестировать
капитал,
полученный
от
ее
пога
шения,
в
другую
дисконтную
облигацию,
со
сроком
погашения
s +
и
и
стоимостью
при
погашении
[1
+ i(s, s +
t)]t[1
+
j(s,
s + t, s +u)]u-t,
где
j(s,
s + t, s +
и)
является
форвардной
ставкой
в
момент
времени
s
для
такой
же
будущей
операции
с
денежными
потоками
в
моменты
времени
s + t
и
s +
u.
Если
отсутствует
возможность
арбитража,
то
окончательные
размеры
капитала
должны
быть
равными,
о
:::;
t
:::;
u.
[1
+i(s, s +
u)]и
=
[1
+i(s, s +
t)]t[1
+
j(s,
s +t, s +u)]u-t,
или
[
'(
]U-t
[1
+i(s,s +
u)]и
1+J s, s +t, s +
и)
=
[1'(
)]t
'
+
't
S,
S +t
Частный
случай,
когда
и
= t +1,
дает
.
[1
+i(s, s +t +1)]t+l
[l+J(s,s+t,s+t+l)]=
[1'(
)]t'
+'t
s,
S +t
а
при
t =
О
(21.5.2)
j(s,
в,
s +1) = i(s, s +1). (21.5.3)
Повторные
применения
формулы
(21.5.3)
с
началом
при
t =
О
дают
[1+i(s,s+t)]t =
[1+j(s,s,s+1)][I+j(s,s+l,s+2)]
..
·[I+j(s,s+t-l,s+t)].
(21.5.4)
Текущая
цена
облигации
с
выплатой
дивидендов
величины
с
по
купонам
в
конце
каждого
из
n
периодов
и
с
выплатой
стоимости
при
погашении
F
может
быть
вы
ражена
с
использованием
цен
дисконтных
облигаций,
а
также
ставок
«спот»-
или
форвардных
ставок,
а
именно,
•
с
использованием
дисконтных
облигаций:
n
С
L
Р(в,
s +k) +
FP(s,
s +n);
k=l
(21.5.5а)
578
Гл.
21.
Проценты
как
случайная
величина
•
с
использованием
ставок
«спот»
:
(21.5.5Ь)
т
= 1,
...
,
n.
(21.5.6)
n
С
L:[1
+i(s, s +k)]-k +
F[l
+i(s, s +
n)]-n;
k=1
•
С
использованием
форвардных
ставок:
n
k-1
n-1
С
L:
П
[1
+
j(s,
s +w, s +w +1)]-1 +F
П
[1
+
j(s,
s +w, s +w +1)]-1.
(21.5.5с)
k=1w=O
w=o
Равенство
этих трех
выражений
ДЛЯ
цены
облигации
основано
на
предположении
об
отсутствии
возможности
арбитража.
Интервалы
времени,
через
которые
производятся
выплаты
по
очередному
купо
ну,
не
всегда
равны
одному
году.
Так,
облигации
Казначейства
США
обычно
имеют
полугодовые
купоны.
Для
облигаций,
рассматривавшихся
в табл.
21.1.1, n =
30
х
2 =
60.
Из
соотношения
(21.5.4Ь)
можно
получить
еще
один
метод
выражения
связи
между
процентными
ставками
и
временем
погашения.
Пусть
задан
набор
ставок
«спот»
в
момент
времени
в,
i(s, s + k), k =
0,1,2,
...
,
и
номинальная
доходность,
обозначаемая
через
у(в,
s +
т),
т.
е.
набор
искусственных
платежей
по купонам,
определяемых
соотношением
m
1 = y{s, s +
т)
L:[1
+i(s, s +k)]-k +
[1
+i(s, s +
т)]-т,
k=1
Номинальная
доходность
может
описываться
как
купонная
ставка
для
обли
гации,
которая
продается
по
ее
стоимости
при
погашении
на
рынке
с
известным
множеством
ставок
«спот»
и
отсутствием
возможности
арбитража.
График
величи
ны
у(в,
s +
n),
рассматриваемой
как
функция
от
n,
называется
1Срuвой
доходности
в
момент
времени
в.
Номинальная
доходность
наиболее
часто
выражается
в
ви
де
доходности
в
облигационно,м.
Э1Свиваленте,
т.
е.
через
полугодовые
номинальные
ставки.
Время
погаmенИJJ
(а)
n
Время
погаmенИJJ
(ь)
n
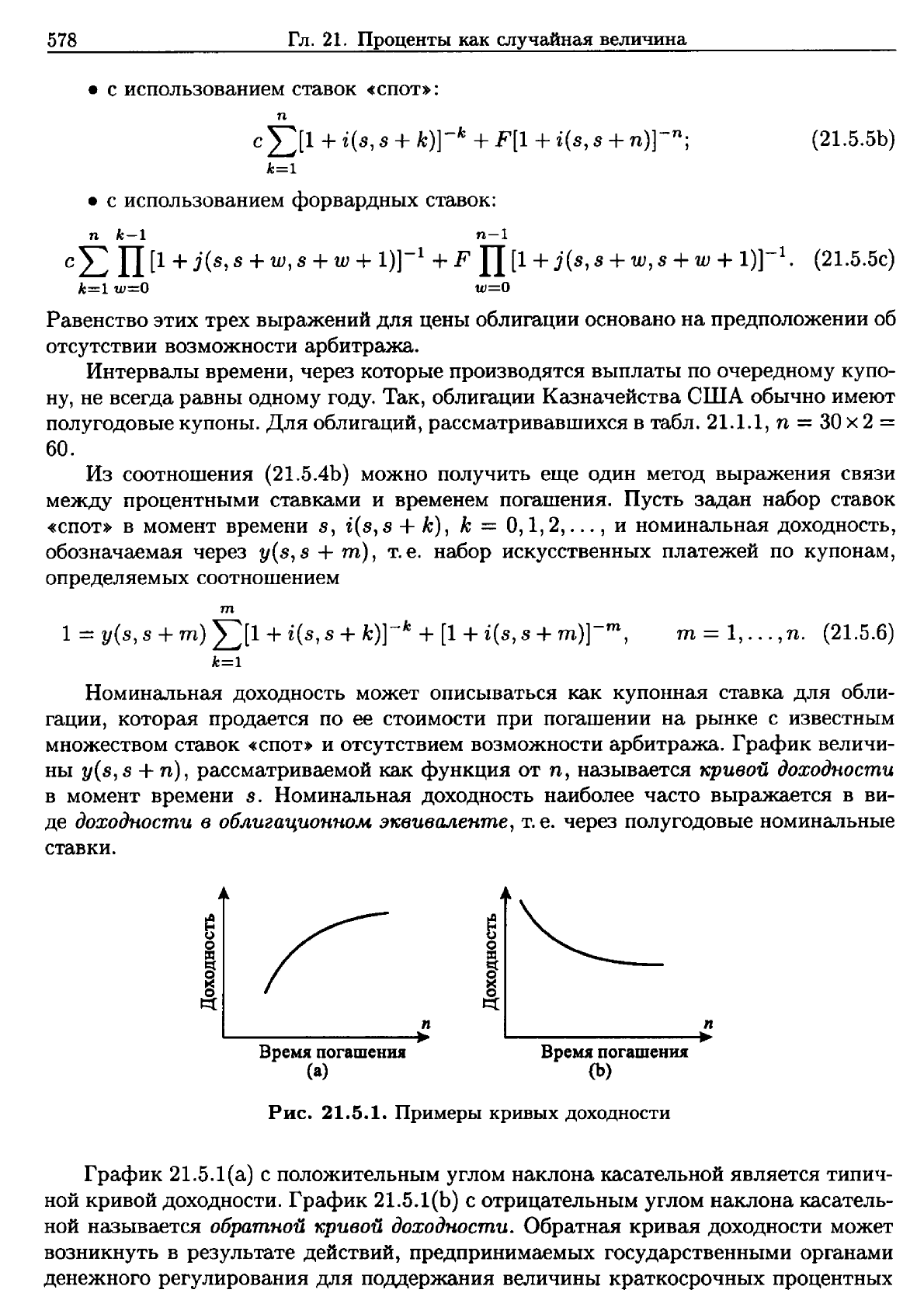
Рис.
21.5.1.
Примеры
кривых
доходности
График
21.5.1(а)
с
положительным
углом
наклона
касательной
является
типич
ной
кривой
доходности.
График
21.5.1(Ь)
с
отрицательным
углом
наклона
касатель
ной
называется
обратной
1Сривой
доходности.
Обратная
кривая
доходности
может
возникнуть
в
результате
действий,
предпринимаемых
государственными
органами
денежного
регулирования
ДЛЯ
поддержания
величины
краткосрочных
процентных

21.5.
Модели
финансовой
экономики
579
ставок
на
высоком
уровне,
чтобы
замедлить
ценовую
инфляцию.
Ожидание
на
рын
ке
капитала
таково,
что
инфляция
будет
краткосрочной
и
долгосрочные
ставки
не
изменятся.
Пример
21.5.1.
Определим
эквивалентные
форвардные
ставки
и
ставки
номи
нальной
доходности
при
следующем
множестве
ставок
«спот.
:
t
i(s,s+t}
1 0,060
2 0,065
3 0,070
Решение.
Воспользовавшись
соотношением
(21.5.2),
получим
.
(1
+
i(s,
s +t +
l)]t+l
1+j(s,s+t,s+t+1)=
{1·(
)]t
+Z
s,s+t
t
j(s,
s +t, s +t +
1}
О
0,06000
1 0,07002
2 0,08007
Воспользовавшись
соотношением
(21.5.5),
получим
( )
1 -
{1
+
i(s,
s +t)]-t
у
S,
S +t = t .
L:
k
=l
[1
+
i(s,
s + k)]-k
t
У(В,
s +
t}
1 0,06000
2 0,06484
3 0,06955
Заметим,
что
все
три
ставки,
рассматриваемые
как
функции
от
t,
имеют
поло-
жительный
угол
наклона
касательной.
..
21.5.2.
Стохастические
модели
В
этом
разделе
мы
проиллюстрируем
метод
генерирования
последовательно
стей
будущих
ставок
номинальной
доходности.
Эти
последовательности,
в
основе
построения
которых
лежит
генерирование
случайных
чисел,
могут
быть
«данными
на
входе»
при
имитационном
моделировании
финансовых
операций,
касающихся
портфеля
страховых или
пенсионных
договоров.
На
практике
чаще
моделируются
ставки
номинальной
доходности,
а
не
форвардные
ставки
или
ставки
«спот»,
по
скольку
эксперты
по
инвестированию
лучше
с
ними
знакомы
и
им
легче
в
этом
случае
выбрать
модель
и
определить
ее
параметры.
Мы
предполагаем,
что
динамика
логарифма
ставок
номинальной
доходности
определяется
модифицированной
авторегрессионной
моделью
первого
порядка:
In[Y(t,n)] =
л(t,
n) +
(1
-
Фn)
In[Y(t -
1,
n)] +
anC:t,n,
t =
0,1,2,
....
(21.5.7)
Слагаемые
в
выражении
(21.5.7)
определяются
следующим
образом:

580
Гл.
21.
Проценты
как
случайная
величина
Y(t,
n)
=
случайная
номинальная
доходность
в
момент
времени
t
для
облигации,
до
погашения
которой
осталось
n
периодов.
Предполагается,
что
насто
ящее
время
-
это
t =
О.
л(t,
n)
=
параметр
сноса,
соответствующий
моменту
времени
t,
для
облигаций,
до
погашения
которых
осталось
n
периодов.
Если
л(t,
n) =
Л
n
,
ТО
формула
(21.5.7)
превращается
в
стандартную
авторегрессионную
модель
первого
порядка
AR(l).
Параметр
сноса
л(t,
n)
для
каждого
t
можно
изменить
таким
образом,
что
будет
удовлетворяться
условие
отсутствия
арбитра
жа
или любое
другое
условие
финансовой
экономики.
(1
-
Фn)
=
авторегрессионный
параметр,
соответствующий
облигациям
со
сроком
погашения
n
периодов.
Параметр
Фn
определяет
скорость
затухания
ра
нее
произошедших
возмущений.
По
этой
причине
в
финансовой
эконо
мике
параметр
Фn
называется
коэффициентом
средней
реверсии.
Для
того
чтобы
получить
модель
стационарных
временных
рядов,
надо,
что-
бы
11
-
Фn
I< 1.
а
n
=
стандартное
отклонение
случайных
возмущений.
ct,n
=
случайные
величины
с
распределением
N(O, 1)
для
облигаций
со
сроком
погашения
через
n
периодов
в
момент
времени
t.
Случайные
величины
ctl,nl
и
Et2,n2
независимы,
если
tl
=f:.
t2,
И
их
корреляция
равна
P
n
l,n2'
если
tl
= t2.
Если
nl
= n2,
то
P
n
l,n2
= 1.
Мы
предполагаем,
что
одно
временные
возмущения
коррелированы.
Замечание.
Модель,
описанная
соотношением
(21.5.7), -
это
только
одна
из
широкого
класса
стохастических
моделей,
которые
могут
применяться
в
рассматри
ваемой
ситуации.
На
выбор
модели
и
на
оценку
параметров
влияют
теория
финансо
вой
экономики
и
анализ
статистических
данных.
Формула
(21.5.7)
также
иллюстри
рует
другой
выбор
средств
при
моделировании
процентных
ставок.
Модели,
опре
деленные
соотношениями
(21.3.1), (21.4.1)
и
(21.4.6а,
Ь и
с),
используют
ln(l
+I
k
),
случайную
интенсивность
начисления
процента
для
периода
k.
Формула
(21.5.7)
ис
пользует
логарифм
величины
У
(t,
n).
Переход
к
логарифму
можно
рассматривать
как средство
стабилизации
дисперсии
наблюдений
или
как
средство,
обеспечиваю
щее
неотрицательность
реализации
величины
У
(t,
n).
Некоторые
актуарии
считают
требование
неотрицательности
важным.
В
упр.
21.9
приводится
модель
случайного
блуждания,
которая
может
считаться
частным
случаем
модели
(21.5.7)
с
1 -
Ф
= 1
и
л
=
О.
Модель
для
процентных
ставок
из
упр.
21.9
обладает
одним
из
свойств
модели
(21.5.7),
а
именно,
в
ней
случайные
процентные
ставки
неотрицательны.
Модели,
подобные
описанной
соотношением
(21.5.7),
можно
применять
для
оце
нивания
кривых
будущей
доходности.
Если
применяется
формула
(21.5.7),
то
оценка
кривых
доходности
потребует
выбора
множества
моментов
погашения
n
и
соответ
ствующих
значений
параметров
Л
n
,
Фn,
О"n
для
каждого
значения
n
и
коэффици
ентов
корреляции
Рnl,n2
для
каждой
пары
выбранных
времен
погашения.
При
этом
число
таких
значений
n
должно
выбираться
достаточно
малым,
чтобы
с
тем
чис
лом
параметров,
которые
необходимо
определить,
можно
было
бы
работать.
Тогда,
пользуясь
множеством
выбранных
случайным
образом
значений
величин
ct,n,
мож
но
будет
определить
вид
кривых
будущей
доходности
при
различных
значениях
t
с
помощью
имитационного
моделирования
будущих
значений
величин
Y(t,
n),
при
меняя
для
выбранных
узловых
значений
времени
погашения
формулу
(21.5.7).
