Бауэрс Н., Гербер Х., Джанс Д., Несбитт С., Хикман Дж. Актуарная математика
Подождите немного. Документ загружается.


Упражнения
511
к
разделу
18.3
18.9.
Выразите
актуарную
настоящую
стоимость
аннуитетов
постнумерандо
С
выпла
той
1000
в
месяц
до
тех
пор,
пока
(а)
ровно одно
ЛИЦО
ИЗ
двух
лиц
(40)
и
(35)
живо
в
течение
последующих
25
лет,
(Ь)
по
крайней
мере
одно
из
двух
лиц
(40)
и
(35)
живо
и
ему
не
более
65
лет,
в
символах
актуарной
настоящей
стоимости
аннуитетов,
сопряженных
со
статусами
дожи
тия
отдельных
лиц
и
всех
лиц
в
группе.
18.10.
Выразите
следующие
величины
в
терминах
аннуитетов
с
гарантированным
пе
риодом
выплат,
а
также
аннуитетов,
сопряженных
со
статусом
дожития
отдельного
лица
и
всех
лиц
из
группы:
(а)
а
х
:
у
:
щ
,
(Ь)
а(25:4Ol):ЗOl'
к
разделу
18.4
18.11.
Пусть
в
каждый
период
времени
интенсивность
смертности
лица
(х)
равна
1/2
от
интенсивности
смертности
лица
(у),
в
то
время
как
интенсивность
смертности
лица
(z)
равна
удвоенной
величине
интенсивности
смертности
лица
(у).
Оцените
вероятность
того,
что
из
трех
указанных
лиц
лицо
возраста
х
умрет:
(а)
первым,
(Ь)
вторым,
(с)
третьим.
18.12.
Какое
из
следующих
равенств
верно?
Поправьте
те,
которые
не
верны,
если
таковые
есть.
- 1
-1
- 1 - 1 - 1
(а)
A
wxyz
= A
wxyz
+A
wxyz
+A
wxyz
+A
wxyz
,
- 3
-2
- 2 - 2 - 2
(Ь)
A
wxyZ
= A
wxyz
+ A
wxyz
+A
wxyz
+A
wxyz
,
- 3
-1
-1
-1
-1
-1
-1
- 1
(с)
A
wxyz
= A
wz
+A
xz
+A
yz
-
(А
wжz
+A
wyz
+A
xyz
) +
А
wжуz
'
18.13.
Запишите
в
форме
определенного
интеграла
актуарную
настоящую
стоимость
страховой
выплаты
в
момент
смерти
лица
(х),
если
это
лицо
пережило
лицо
(у).
Размер
выплаты
равен
времени,
прошедшему
между
заключением
договора
и
датой
смерти
ли
ца
(у).
18.14.
Предполагая,
что
выполняется
закон
Гомперца
и
#-,(40)
=0,003, Jl(56) = 0,012,
вычислите
(а)
ooq40:~:i;56,
(Ь)
ooq40:4
2
S:56'
[Замечание.
В
п.
(а)
обозначение
2:З
отражает
событие,
что
лицо
(48)
умрет
вторым
или
третьим
в
указанной
группе
лиц.]
18.15.
Выплата
размера
1
по
договору
страхования,
заключенному
лицами
(х),
(у)
и
(z),
осуществляется
в
момент
смерти
лица
(z)
только
в
случае,
если
лицо
(х)
умерло
не
менее
чем
за
10
лет
до
этого,
а
лицо
(у)
умерло
менее
10
лет
назад.
Выразите
акту
арную
настоящую
стоимость
этой
страховой
выплаты
в
терминах
актуарных
настоящих
стоимостей
страховых
выплат
на
случай
смерти
и на
дожитие.
18.16.
Выведите
формулу,
не
содержащую
интегралов,
для
актуарной
настоящей
сто
имости
выплаты
размера
1
через
10
лет
после
смерти
лица
(х)
при
условии,
что
одно
или
оба
лица
(у)
и
(z)
пере
живут
лицо
(х)
и
умрут
до
окончания
этого
10-летнего
периода.
18.17.
Получите
формулу
дЛЯ
единовременной
брутто-премии
по
договору
страхова
ния
с
выплатой
размера
1,
если
лицо
(ЗО)
умрет
раньше
лица
(60)
или
в
течение
5
лет
после
смерти
последнего,
с
возвратом
единовременной
брутто-премии
без
учета
процента
в
конце
пятилетнего
строка
после
смерти
лица
(60),
если
по
этому
договору
не
предъяв
лялось
требования
о
выплате
в
связи
со
смертью
лица
(30).
Предположите,
что
надбавка
составляет
7,5%
от
нетто-премии.
к
разделу
18.5
18.18.
Не
используя
предположения
о
независимости,
выведите
соотношения
типа
112
пqWЖ1l
=
пqwжуz
+
пqwжуz
1
И
используйте
их
для
получения
результата
примера
18.4.1.

512
Гл.
18.
Развитие
теории
для
нескольких
лиц
18.19.
Не
используя
предположение
о
независимости,
выведите
соотношения
- 1 - 1 - 2
-1
- 1 - 2
Аху
=
А
ху,;:
+
А
ху
.
и
А
у,;:
=
А
ху.:
+
А
жуz
1 1
И
используйте
их
для
получения
результата
примера
18.4.2.
18.20.
Выразите
схЛw;уz
1
(а)
в
виде
определенного
интеграла,
(Ь)
в
терминах
вероятностей
смерти
с
учетом
порядка
смертей
в группе.
18.21.
Предполагая, что
выполняется
закон
Гомперца,
покажите, что
су
(а)
tqx;
=
tqy
-
с
х
+
су
tqжу
j
-
3
с
х
-
с
.:
-
су
с
.:
-
(Ь)
А
ху.:
=
А
.;:
-
А
у.;:
+ A
xyz
.
1
с
х
+
сУ су
+
с
.:
с
х
+
су еЖ
+
су
+
с
.:
18.22.
Вычислите
(а)
ооq20:4
2
О:БО,
(Ь)
ooq20:40:io,
(с)
ooq20}O,
1
если
для
лиц
(20), (40)
и
(60)
интенсивность
смертности
определяется
формулой
рх
=
1/(100-
х)
при
О
<
х
< 100.
Это
показывает,
что
соотношение
ooqx;z =ooq;yz
ooq~z,
которое
1
справедливо,
если
выполняется
закона
Гомперца,
в
общем
случае
неверно.
18.23.
На
основе
таблицы
смертности,
соответствующей
закону
Гомперца
(при
с
8
=2),
- - -
-2
А
54
= 0,3,
А
б2
=0,4
и
А
70
=0,52.
Определите
А54:54:б2'
1
-
-1 -1
-1
18.24.
Пусть
А
щ
=0,6,
А
щх
= 0,3,
А
щхх
= 0,2,
А
щххх
=0,1.
Вычислите
-2
-4
-4
(а)
А
щххх
,
(Ь)
А
щххх
,
(с)
А
шххх
.
122
18.25.
Выразите
в
интегральной
форме
вероятность
того,
что
лица
(х),
(у)
и
(z)
умрут
в
указанном
порядке
в
течение
следующих
25
лет,
причем
между
любыми
двумя
смертями
пройдет
не
менее
1
О
лет.
18.26.
Выразите
в
интегральной
форме
вероятность
того,
что
лица
(10), (20)
и
(30)
умрут
до
достижения
60-летнего
возраста,
причем
лицо
(20)
умрет
вторым.
18.27.
Пусть
ooq;y = 0,5537, ooq;z = 0,6484, ooq;yZ =0,5325
и
ooqx;z =
ooqxy~.
Вычис
2
лите
qxyz,
18.28.
В
соответствии
с
некоторой
таблицей
смертности
вероятность
того,
что
три
лица
(70), (55)
и
(40)
умрут
в
указанном
порядке
с
интервалами
не
менее
15
лет,
составляет
0,048,
а
вероятность
того,
что
по
крайней
мере
одно
лицо
из
двух
лиц
(70)
будет
живо
в
течение
15
лет
до
момента
смерти
лица
(55),
составляет
0,8.
Вычислите
вероятность
того,
что
ни
одно
из
двух
лиц
(40)
не
доживет
до
возраста
70
лет.
18.29.
Какие
из
следующих
выражений
верны?
Исправьте
неверные,
если
таковые
имеются.
- 3
100
t -
(а)
A
wxyz
= V tqw tpxyz
Itx(t)
АуН
dtj
12
о
(Ь)
{
1О
(1
- t+10P50)
tP60
J.lбо(t)
dt
+
/00
(t-10P50 - t+10P50)
tРБО
J.Lбо(t)
dt
Jo
10
=
{
1О
(1
_
t+10РБО)
tp50
J.L50(t)
dt
+
/00
(t-10РБО
- t+10P60)
tРБО
J.L50(t)
dt;
J
o
10
(
)
1 2 1
С
зоq40:50:БО
+
зоq40:50:60
=
зоq40:50:БО'
к
разделу
18.6
18.30.
Запишите
выражение,
не
использующее
интегралов,
для
актуарной
настоящей
стоимости
аннуитета,
выплачиваемого
непрерывно
с
интенсивностью
1
в
год
(а)
в
течение
жизни
лица
(у)
и
10
лет
после
его
смерти
при
условии,
что
выплаты
не
производятся,
пока
живо
лицо
(х),

Упражнения
513
(Ь)
в
течение
жизни
лица
(у)
и
10
лет
после
его
смерти
при
условии,
что
выплаты
не
производятся,
пока
живо
лицо
(х),
или
если
лицо
(у)
умрет
раньше
лица
(х).
18.31.
В
символах
актуарных
настоящих
стоимостей
аннуитетов
и
договоров
страхова
ния
жизни
выразите
единовременную
брутто-премию
(с
надбавкой
8%),
обеспечивающую
страховые
выплаты
в
виде
аннуитета,
сопряженного
со
статусом
дожития
последнего
из
двух
лиц
(х)
и
(у),
отсроченного
на
n
лет,
с
ежегодНЫМИ
выплатами
размера
1,
умень
шаемыми
на
1/3
в
случае
первой
смерти,
с
учетом
следующих
условий:
если
смерть
лица
(х)
произошла
первой
и
в
течение
периода
отсрочки,
то
выплата
уменьшенного
аннуитета
начинается
спустя
год
после
этой
смерти,
а
если
смерть
лица
(х)
произошла
второй
и
в
течение
периода
отсрочки,
то
единовременная
брутто-премия
возвращается
в
конце
года
смерти.
18.32.
В
разд.
18.6
реверсивный
аннуитет
начинал
выплачиваться,
если
статус
(и)
сохранялся
после
потери
статуса
(v).
Это
соображение
может
быть
распространено
на
аннуитеты
с
выплатами,
начинающимися
после
наступлении
двух
или
более
смертей
в
указанном
порядке.
(а)
Покажите,
что
ax~l::
=
ayl::
-
ax~I::'
(Ь)
На
основе
таблицы
смертности,
соответствующей
закону
Гомперца,
докажите,
что
с
х
су
а
21
-
а
-
а
+
а
ху
::
-
сх
+
сУ::
у::
сХ
+
су
xyz·
к
разделу
18.7
18.33.
Выразите
ежегодНУЮ
нетто-премию
по
договору
страхования
на
дожитие
с
вы
платой
размера
1
при
условии,
что
лицо
(х)
проживет
n
лет
после
смерти
лица
(у).
18.34.
Какую
актуарную
настоящую
стоимость
аннуитета
следует
использовать
для
вычисления
ежегодной
нетто-премии,
соответствующей актуарной
настоящей
стоимости
А
2 ?
r
xyz
'
Ко
всем
темам
главы
18.35.
Договор
страхования,
в
котором
страховым
случаем
является
смерть
лица
(х)
ранее
возраста
х+n
лет
и
смерть
лица
(у)
ранее
возраста
у+т,
причем
т
<
n,
обеспечивает
выплату
размера
1
в
конце
года
второй
смерти.
(а)
Покажите,
что
актуарная
настоящая
стоимость
выплаты
может
быть
выражена
в
виде
A
x
1
y
:
Тiil
+v
m
тРх
(1
-
тРу
)Ax~m:n-ml'
(Ь)
Какая
актуарная
настоящая
стоимость
аннуитета
может
быть
использована
для
вычисления
ежегодной
нетто-премии?
18.36.
Группа
из
т
лиц
получает аннуитет
с
годовой
выплатой
размера
1,
сопря
женный
со
статусом
дожития
последНего
лица
в
группе,
с
распределением
дохода
средИ
доживших
равными
долями.
Актуарная
настоящая
стоимость
доли
лица
(Xl)
составляет
m-l
'"'
1 _
и]
~
j + 1
аХl:Х2Хз·
..
Хm
•
з=0
Покажите,
что
эта
актуарная
настоящая
стоимость
может
быть
записана
в
виде
111
а:
ч
-
2"(а
Х1Х2
+
...
+
Q,XIX
m
)
+
з(аХIХ2ХЗ
+ ... +
aXIXm-lХm)
-
•..
(_1)m-l
т
aXlX2
..
·X
....
m-l
[
Указание.
Используйте
теорему
18.2.1
для
выражения
"
~1
tP
x
х
Ш.]
L-
1 +
2·
.....
j=O
18.37.
Дайте
словесную
интерпретацию
выражения
{СО
t - 1
10
V tqx tPyz
Jly(t)A
z
+
t
:
IOl
dt.
17
-
1855

514
Гл.
18.
Развитие
теории
для
нескольких
лиц
18.38.
Пусть
в
обозначениях
теоремы
18.2.2
А
1
=
{Т(у)
< min[n,
Т(х),
T(z)J},
А
2
=
{Т(у)
< min[n,
Т(х),
T(w)J},
Аз
=
{Т(у}
< min[n,
T(w),
T(z)J}.
Покажите,
что
событие
А
из
примера
18.4.1
совпадает
с
событием,
которое
осуществляется,
если
происходит
в
точности
одно
из
событий
А
1
,
А
2
И
Аз.
Следовательно,
используйте
те
орему
18.2.2
для
получения
результата
примера
18.4.1
без
предположения
о
независимости.
[Указание.
Покажите,
что
Р(А
1
)
=
nqw:z:tz,
Р(А
1
А
2
}
=
Р(А
1
А
з
}
=
Р(А
2
А
з
}
=
Р(А
1
А
2
А
з
)
=
nqw:z:~z
И
Р[Аl
(неА
2
)(неА
з
)]
=
nqw:z:;z
.]
1
18.39.
Рассмотрите
договор
бессрочного
страхования
на случай
второй
смерти
с
пр
е-
миями,
выплачиваемыми
до
тех
пор,
пока
живо
по
крайней
мере одно
лицо
из
пары
(х)
и
(у),
предполагая,
что
модель
дискретна.
(а)
Покажите,
что
kV7l:y
= 1 -
a:z:y+k/aXfj,
где
..
kPx
ax+k
+
kPy
ay+k
-
kPx
kPy
ax+k:y+k
a:z:y+k =
kP:z:
+
/еРу
-
1сРх
1сРу
(Ь)
Покажите,
что
axy+k
можно
вычислить
по
формуле
00
..
1
'"'"'
j
a:z:y+k = k
~
V
jРжУ.
V
/еРхУ
j==k

19
МАТЕМАТИЧЕСКАЯ
ДЕМОГРАФИЯ
19.1.
Введение
Многие
соображения,
использованные
в
гл.
З,
проистекают
из
математической
демографии.
Например,
функция
дожития,
посредством
которой
определялось
рас
пределение
случайной
величины
продолжительности
предстоящей
жизни
и
описы
валось
изменение
во
времени
некоторой
совокупности
дожития,
играет
важную
роль
в
построении
демографических
моделей.
В
этой
главе
излагаются
общие
модели.
С
необходимыми
изменениями
их
можно
применять
к
населению
страны
или
региона,
к
трудоспособному
населению
или
к
совокупностям
животных
в
дикой
природе.
Нас,
в
частности,
будут
интересовать
некоторые
актуарные
приложения
матема
тической
демографии.
В
разд.
19.5
модель
математической
демографии
применяется
к
исследованию
динамики
определенной
схемы
страхования
жизни
для
некоторой
группы
населения.
В
гл.
20
модель
математической
демографии
используется как
составная
часть
модели,
предназначенной
для
исследования
динамики
некоторой
системы
пенсионного
обеспечения
группы
населения.
19.2.
Диаграмма
Лексиса
В
этом
разделе
мы
введем
удобный
метод
описания
изменения
численного
соста
ва
какой-либо
группы
населения!)
во
времени.
Например,
период
работы
отдельных
лиц
можно
изобразить
параллельными
отрезками
на
двумерной
диаграмме,
называ
емой
диаграммой
Ле?Ссиса
(см.
рис.
19.2.1).
Точка
вступления
лица
в
группу
работ
ников
(координатами
которой
являются
время
и
возраст
вступления)
обозначена
светлым
кружком,
-
один
из
концов
отрезка,
сопоставленного
этому
лицу.
Пре
бывание
в
этой
группе
изображается
наклонным
отрезком,
второй
конец
которого,
обозначенный
черным
кружком
(его
координаты
-
это
время
и
возраст
выбытия),
означает
выбытие
из
группы
работников.
На
рис.
19.2.1
видно,
что
в
рассматриваемую
группу
работников
в
момент
вре
мени
-
25
по
отношению
к
настоящему
времени
(t =
О)
входили
три
лица.
В
настоя
щий
момент
времени
(t
=
О)
останется
два
работника.
Могут
представлять
интерес
утверждения
о
продолжительности
их
предстоящей
работы.
Штриховые
линии
на
рис.
19.2.1
изображают
длительность
предстоящей
работы
двух
лиц,
являющихся
работниками
в
настоящее
время.
В
следующих
замечаниях
приведены
характерные
черты
диаграммы
Лексиса.
1)
Иногда
для
краткости
мы
будем
говорить
просто
сгруппа.
или
снаселение
•.
-
Прu.м..
реа.
17'"
516
Гл.
19.
Математическая
демография
Настоящее
время
-50 -40 -30 -20
-1
О О
1
О
20 30
Время
10
20
30
40
50
60
Возраст
о
точка
вступления
•
точка
выбытия
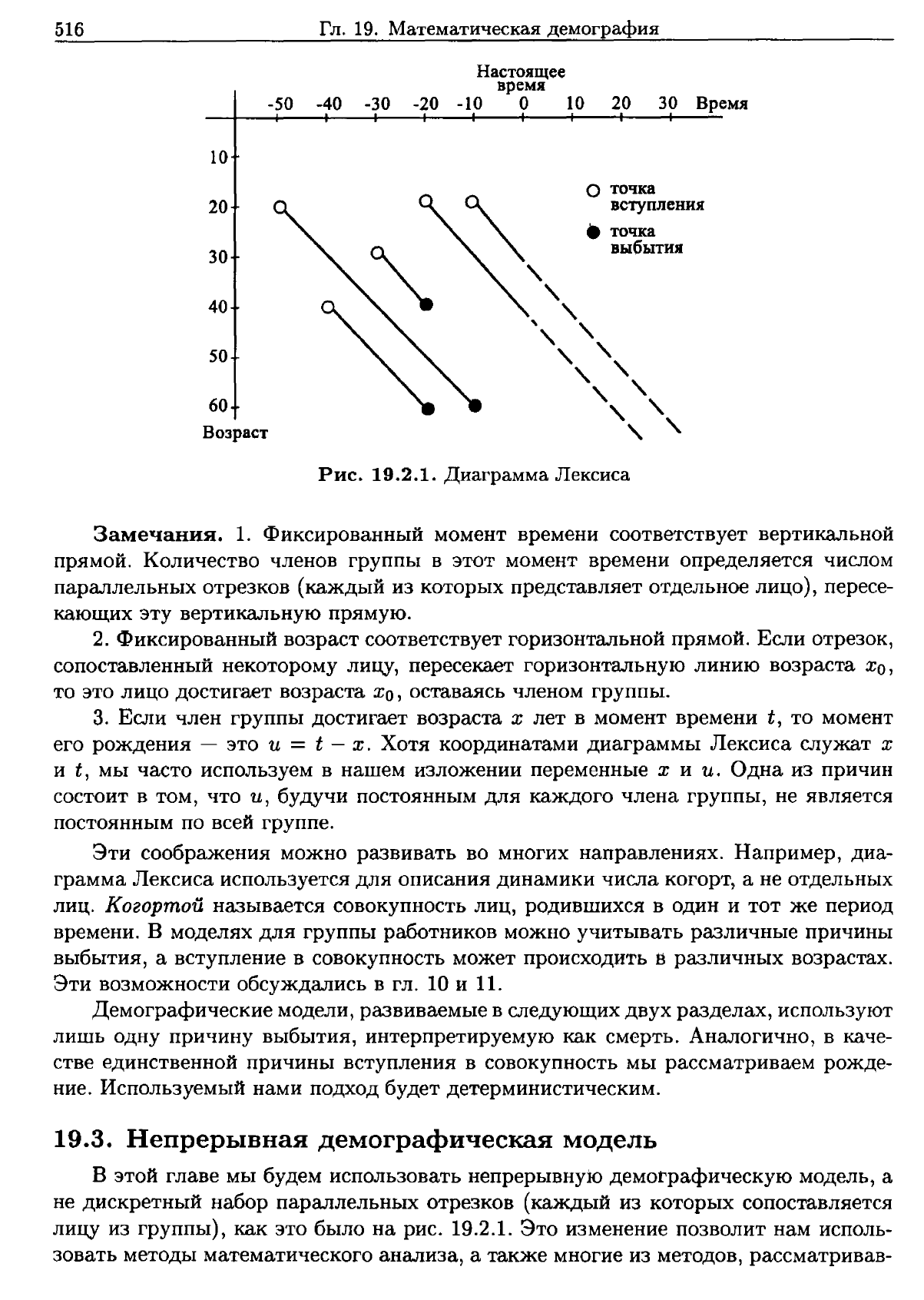
Рис.
19.2.1.
Диаграмма
Лексиса
Замечания.
1.
Фиксированный
момент
времени
соответствует
вертикальной
прямой.
Количество
членов
группы
в
этот
момент
времени
определяется
числом
параллельных
отрезков
(каждый
ИЗ
которых
представляет
отдельное
лицо),
пересе
кающих
эту
вертикальную
прямую.
2.
Фиксированный
возраст
соответствует
горизонтальной
прямой.
Если
отрезок,
сопоставленный
некоторому
лицу,
пересекает
горизонтальную
линию
возраста
Хо,
то
это
лицо
достигает
возраста
Ха,
оставаясь
членом
группы.
3.
Если
член
группы
достигает
возраста
Х
лет
в
момент
времени
t,
то
момент
его
рождения
-
это
и
= t -
Х.
Хотя
координатами
диаграммы
Лексиса
служат
Х
и
t,
мы
часто
используем
в
нашем
изложении
переменные
Х
и
u.
Одна
из
причин
состоит
в
том,
что
и
,
будучи
постоянным
для
каждого
члена
группы,
не
является
постоянным
по
всей
группе.
Эти
соображения
можно
развивать
во
многих
направлениях.
Например,
диа
грамма
Лексиса
используется
для
описания
динамики
числа
когорт,
а
не
отдельных
лиц.
Когортой
называется
совокупность
лиц,
родившихся
В
один
И
тот
же
период
времени.
В
моделях
для
группы
работников
можно
учитывать
различные
причины
выбытия,
а
вступление
в
совокупность
может
происходить
13
различных
возрастах.
Эти
возможности
обсуждались
в
гл.
10
и
11.
Демографические
модели,
развиваемые
в
следующих
двух
разделах,
используют
лишь
одну
причину
выбытия,
интерпретируемую
как
смерть.
Аналогично,
в
каче
стве
единственной
причины
вступления
в
совокупность
мы
рассматриваем
рожде
ние.
Используемый
нами
подход
будет
детерминистическим.
19.3.
Непрерывная
демографическая
модель
В
этой
главе
мы
будем
использовать
непрерывную
демографическую
модель,
а
не
дискретный
набор
параллельных
отрезков
(каждый
из
которых
сопоставляется
лицу
из
группы),
как
это
было
на
рис.
19.2.1.
Это
изменение
позволит
нам
исполь
зовать
методы
математического
анализа,
а
также
многие
из
методов,
рассматривав-

19.3.
Непрерывная
демографическая
модель
517
шихся
в
предыдущих
главах.
Можно
было
бы
вести
параллельное
изложение
для
дискретной
модели,
используя
методы
линейной
алгебры.
Итак,
мы
будем
предполагать,
что
все
вступления
в
группу
населения
-
ро
ждения,
а
все
выбытия
-
смерти.
Миграция
в
модели
исключается.
Рождения
про
исходят
непрерывно,
и
Ь(
и)
обозначает
функцию
плотности
ро:нсдений
в
момент
времени
u.
Таким
образом,
Ь(и)
du
есть
число
рождений
между
моментами
времени
и
и
и
+ du.
Обозначим
через
В(Х,
и)
функцию
дожития
лиц,
рожденных
в
момент
времени
и.
Она
называется
фУН'I'цией
до:нситuя
nО'l'оления.
Положим
l(x,
и)
=
Ь(и)
В(Х,
и).
(19.3.1)
Эта
функция
l(х,
и}
называется
фУ'Н'I'цией
nлот'Ности
группы
насел.ения.
Интерпретация
функции
l(х,
и)
упрощается
обращением
к
непрерывному
вари
анту
диаграммы
Лексиса
(см.
рис.
19.3.1).
Этот
и
последующие
рисунки
данного
раздела
являются двумерными.
Они
призваны
облегчить
интерпретацию
диффе
ренциалов
или
показать
области
интегрирования.
В
каждом
случае
следовало
бы
использовать
трехмерное
изображение,
рисуя
функцию,
определенную
на
плоско
сти
«возраст-время»'.
о и
u+du
t t
+dt
Вемя
х
Возраст
1(x,u)du =
l(x,t-x)dt
(19.3.3)
Рис.
19.3.1.
Интерпретация
функции
l(x,
и)
Из
[(О,
и)
du =
Ь(и}
du
лиц,
рожденных
между
моментами
времени
u
и
и
+ du,
до
возраста
Х
лет
доживает
l(х,
и)
du
лиц.
Пусть
t =
х
+
и;
тогда
dt
= du
и
это
выражение
можно
переформулировать:
1
(х,
t -
х)
dt
=
(число
лиц,
доживших
до
возраста
х
в
моменты
времени
между
t
и
t +
dt).
(19.3.2)
Отсюда
следует,
что
число
лиц,
доживших
до
возраста
х
лет
в
моменты
времени
между
to
и
tl,
равно
1
tt
l(х,
t -
х)
dt.
to
Теперь
рассмотрим
другой
вопрос.
Пусть
хо
<
хl
-
два
фиксированных
возраста,
а
to
-
заданный
момент
времени.
Какое
количество
лиц
в
возрасте
между
ХО
и
Хl
будет
живо
в
момент
времени
to?
В
этом
вопросе
под
«количеством
лиц»'
под
разумевается
значение
интеграла
от
функции
l(x,
и),
как
в
гл.
3,
а
не
переменная,
принимающая
только
целые
значения.

518
Гл.
19.
Математическая
демография
Эти
лица
достигают
возраста
хо
между
моментами
времен.и
to
-
(Xl
-
Хо)
и
to,
а
затем
доживают
до
момента
времени
to,
как
показано
на
рис.
19.3.2.
Диагональная
пунктирная
линия
показывает
типичную
когорту
лиц,
которые
достигнут
возраста
между
Хо
и
Xl
В
момент
времени
to.
Время
"
"
"
"
"
(19.3.5)
(19.3.4)
Возраст
Рис.
19.3.2.
Число
лиц
в
возрасте
между
ХО
и
Xl
В
момент
времени
to
Таким
образом,
число,
которое
мы
ищем,
-
это
l
to
l( ) s(xo +
to
- t, t -
ХО)
d
Хо,
t -
Ха
( ) t .
tO-(ХI-ХО)
S
Хо,
t -
ха
При
вычислении
интеграла
(19.3.4)
для
того,
чтобы
записать
подынтегральное
вы
ражение
в
виде
b(t -
Ха)В(Хо
+
to
- t, t -
Хо)
= l(xa +
to
-
t,
t -
ХО),
мы
можем
использовать
формулу
(19.3.1).
Положим
х
=
Хо
+ (to - t).
Тогда
интеграл
(19.3.4)
можно
переписать
в
виде
l
ХО
lXl
- l(x,
to
-
х)
dx = l(x,
to
-
х)
dx.
Xl
ХО
Из
этого
равенства
следует,
что
l(x,
to
-
х)
dx
==
(число
лиц
в
возрасте
между
Х
и х
+ dx
в
момент
времени
to).
(19.3.6)
Следовательно,
функция
плотности
группы
населения
имеет
две
интерпретации.
Первая
следует
из
формул
(19.3.2)
и
(19.3.3)
и
относится
к
числу
лиц,
достигших
возраста
Х
между
моментами
времени
t
и
t +dt.
Вторая
следует
из
формул
(19.3.5)
и
(19.3.6)
и
относится
к
числу
лиц
в
возрасте
между
х
и
x+dx
в
момент
времени
to.
Эти
две
интерпретации
соответствуют
выделению
слоев
на
диаграмме
Лексиса
для
рассматриваемой
группы;
в
первой
интерпретации
это
слой
между
вертикальными
прямыми,
проходящими
через
точки
t
и
t +dt,
а
во
второй
-
слой
между
горизон
тальными прямыми,
проходящими
через
точки
х и х
+ dx.
Для
того
чтобы
ввести
в
нашу
модель
смертность,
положим
1
а
1 8
р(х,
и)
==
- ( )
-8
s(x,
и)
==
-l(
)
-8
l(x,
и);
S х,и
х
Х,и
х
(19.3.7)
это
интеНСUбность
смертности
nох;о.ленuя
в
возрасте
х
для
лиц,
родившихся
В
мо
мент
времени
u.
На
рис.
19.3.3
даются
три
интерпретации
этого
определения.
Они
19.3.
Непрерывная
демографическая
модель
519
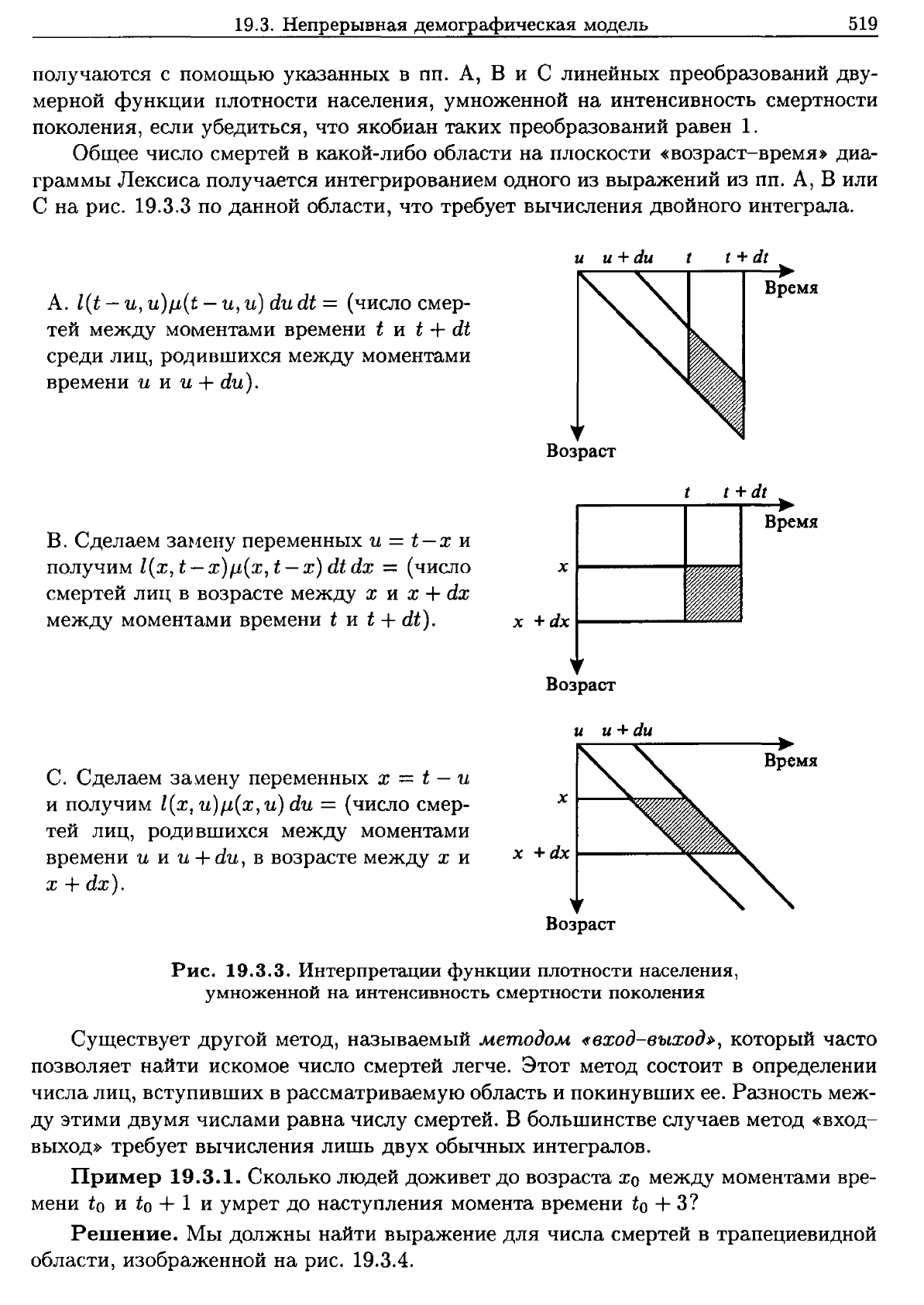
получаются
с
помощью
указанных
в
пп.
А,
В
и
С
линейных
преобразований
дву
мерной
функции
плотности
населения,
умноженной
на
интенсивность
смертности
поколения,
если
убедиться,
что
якоби
ан
таких
преобразований
равен
1.
Общее
число
смертей
в
какой-либо
области
на
плоскости
«возраст-время»
диа
граммы
Лексиса
получается
интегрированием
одного
из
выражений
из
пп.
А,
В
или
С
на
рис.
19.3.3
по
данной
области,
что
требует
вычисления
двойного
интеграла.
и и
+du
t
t
+ dt
А.
l(t
-
и,
u)jj(t
-
и,
и)
du
dt
=
(число
смер
тей
между
моментами
времени
t
и
t + dt
среди
лиц,
родившихея
между
моментами
времени
и
и
и
+
du).
Возраст
Время
t t + dt
В.
Сделаем
занену
переменных
u =t -
х и
получим
l(x,
t-х)lJ(х,
t-x)
dtdx
=
(число
смертей
лиц
в
возрасте
между
х
и х
+
dx
между
момеН'Iами
времени
t
и
t +dt).
xl------
х
+
dx
1------
Время
С.
Сделаем
замену
переменных
х
= t - u
и
получим
l(x,
u)jj(x,
и)
du
=
(число
смер
тей
лиц,
РОДI1
вшихея
между
моментами
времени
u
и
u +
du,
в
возрасте
между
х и
х
+
dx).
Возраст
и и
+du
х
+
dx
1-----....;
Возраст
Время
Рис.
19.3.3.
Интерпретации
функции
плотности
населения,
умноженной
на
интенсивность
смертности
поколения
Существует
другой
метод,
называемый
,м,етодо,м,
«вxoд-вЪtXoд~,
который
часто
позволяет
найти
искомое
число смертей
легче.
Этот
метод
состоит
в
определении
числа
лиц,
вступивших
в
рассматриваемую
область
и
покинувших
ее.
Разность
меж
ду
этими
двумя
числами
равна
числу
смертей.
В
большинстве
случаев
метод
«вход
выход»
требует
вычисления
лишь
двух
обычных
интегралов.
Пример
19.3.1.
Сколько
людей
доживет
до
возраста
хо
между
моментами
вре
мени
to
и
to
+ 1
и
умрет
до
наступления
момента
времени
to
+3?
Решение.
Мы
должны
найти
выражение
для
числа
смертей
в
трапециевидной
области,
изображенной
на
рис.
19.3.4.

520
Гл.
19.
Математическая
демография
t
o
+ 1 t
o
+2 t
o
+ 3
I I I
Время
I
...
Возраст
u=t-x
О
Вход
----
Рис.
19.3.4.
Область,
в
которой
подсчитывается
число
смертей
для
примера
19.3.1
Метод
двойного
интеграла:
используя
интерпретацию
на
рис.
19.3.3С,
мы
полу-
чим
для
числа
смертей
выражение
l
to+l-xo
ltо+з-u
l(x, u)J.l(x,
и)
dx du.
to
-хо
хо
Используя
формулу
(19.3.7),
получим
для
числа
смертей
выражение
l
to+l-xo
ltо+з-u
[
8l(x
и)]
lto+l-xo
-
д
' dx du =
[l
(хо
,
и)
- 1
(to
+3 -
и,
и)]
du
to-xo
хо
Х
to-xo
l
to+l-xo
lto+l-xo
= l(xo,
и)
du -
l(t
a
+3 -
и,
и)
du.
to-xo
to-xo
Положив
В
первом
интеграле
у
=
и
+
хо,
а
во
втором
w =
to
+ 3 -
и,
придем
к
следующей
формуле
для
числа
смертей:
l
tO
+
1
lХО+3
l(xo,
У
-
ха)
dy - l(w,
to
+3 - w) dw.
~
хо+2
Метод
-«BXOД-BЫXOД~:
для
того
чтобы
получить
искомое
число
смертей,
найдем
разность
между
числом
вступивших,
т.
е.
тех,
которые
достигли
возраста
ха
между
моментами
времени
to
и
to
+1,
и
числом
выбывших,
т.
е.
тех,
которые
дожили
до
возрастов
между
хо+2
и
Хо+З
в
момент
времени
tо+З.
Используя
формулы
(19.3.3)
и
(19.3.5),
получаем
l
tO
+
1
lХО+З
l(xo,
У
-
хо)
dy - l(w,
to
+3 - w) dw,
to
хо+2
что
совпадает
с
результатом,
полученным
с
помощью
двойного
интеграла.
У
Пример
19.3.2.
Определим
число
лиц,
находящихся
в
возрасте
между
20
и
40
годами
в
момент
времени
to,
которые
умрут
до
достижения
возраста
70
лет.
Решение.
Необходимо
найти
выражение
для
числа
смертей
в
трапециевидной
области,
изображенной
на
рис.
19.3.5.
