Бауэрс Н., Гербер Х., Джанс Д., Несбитт С., Хикман Дж. Актуарная математика
Подождите немного. Документ загружается.

18.5.
Сложные
актуарные
функции,
зависящие
от
очередности
смертей
501
T(z) =
и
s<7+5
T(z)
=
и
r+5<s<r+5
и
=r +10
и
=r +10
r +10
"='+5
г+l0
t=s
t=s~
и
=1
и
=1
г+5
r+5
r
s
(А)
s + 5
T(y)=t
7
s + 5
Т(у)=!
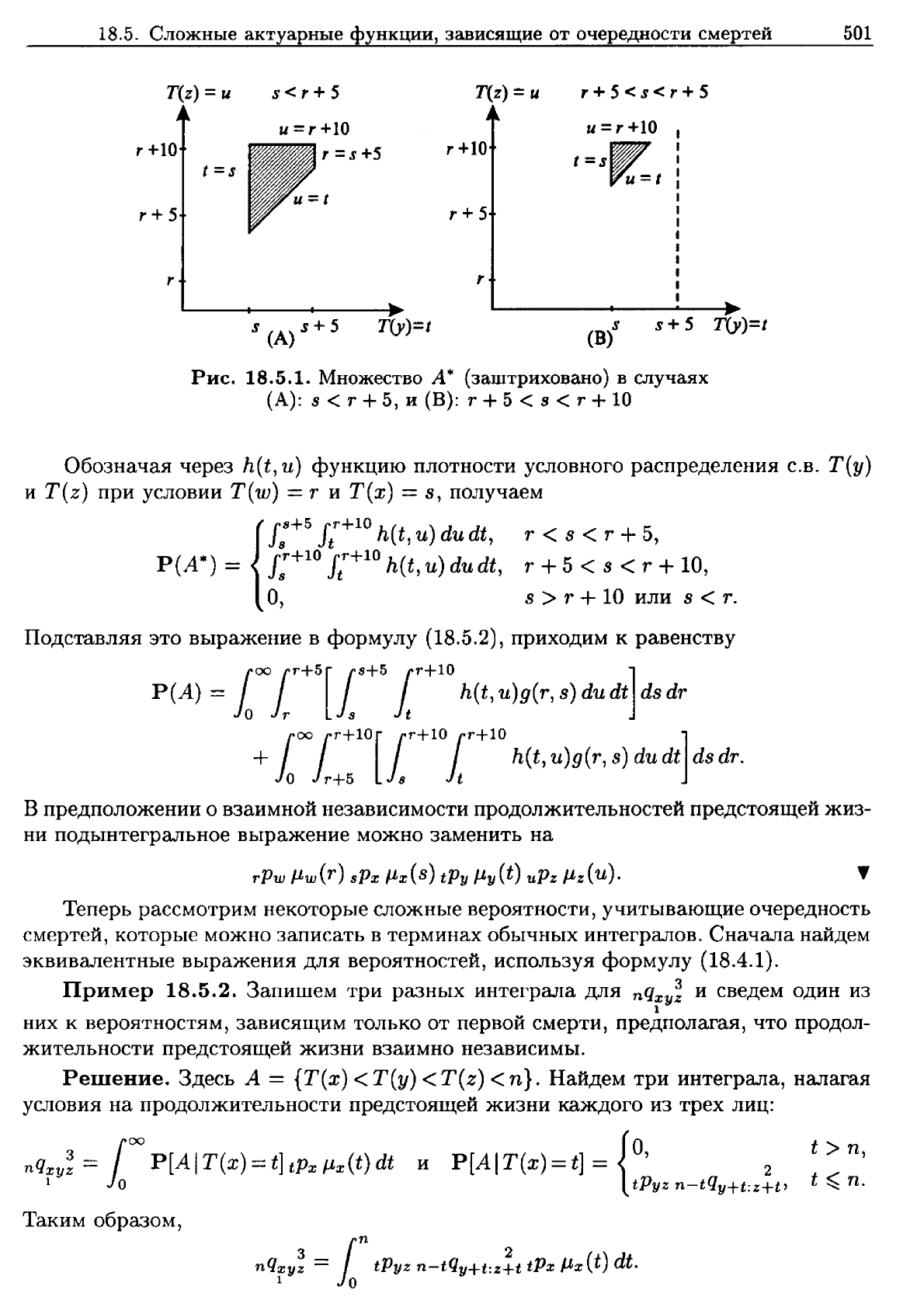
Рис.
18.5.1.
Множество
А'"
(заштриховано)
в
случаях
(А):
s < r +5,
и
(В):
r +5 < s < r +
10
Обозначая
через
h(t,
и)
функцию
плотности
условного
распределения
С.в.
Т(у)
и
T(z)
при
условии
T(w)
= r
и
Т(х)
=
В,
получаем
{
{в+5
rr+l0
h(t
) d dt 5
Js
Jt
,и
и
, r < s < r + ,
Р(А*)
=
J:+
10
Jt
r
+
1o
h(t,
и)
du dt, r +5 < s < r + 10,
о,
s > r +10
или
s <
т.
Подставляя
это
выражение
в
формулу
(18.5.2),
приходи
м
К
равенству
Р(А)
=
[""
1,+5[/.Н51'+1О
h(t,u)g(r, s)
du
dt]
ds
dr
+
{"
1::10[[+10[+10
h(t,u)g(r, s)
du
dt]
ds
dr.
В
предположении
о
взаимной
независимости
продолжительностей
предстоящей
жиз
ни
подынтегральное
выражение
можно
заменить
на
rPw
рш(т)
вРх
IJx(S) tPy
J.ly(t)
upz
J.lz(U).
Теперь
рассмотрим
некоторые
сложные
вероятности,
учитывающие
очередность
смертей,
которые
можно
записать
в
терминах
обычных
интегралов.
Сначала
найдем
эквивалентные
выражения
для
вероятностей,
используя
формулу
(18.4.1).
При
мер
18.5.2.
Запишем
три
разных
интеграла
для
nqxy~
И
сведем
один
из
1
них
К
вероятностям,
зависящим
только
от
первой
смерти,
предполагая,
что
продол-
жительности
предстоящей
жизни
взаимно
независимы.
Решение.
Здесь
А
=
{Т(х)
<
Т(у)
<
T(z)
<
n}.
Найдем
три
интеграла,
налагая
условия
на
продолжительности
предстоящей
жизни
каждого
из
трех
лиц:
nqxy~
=
Г:Ю
Р[А
I
Т(х)
=
t]
tPx
J.lx(t)
dt
1
Jo
Таким
образом,
и
P[AIT{x)=t]
=
{о,
2
tPyz
n-tQу+t:z+t,
t >
n,
t
~
n.
nqxy~
=
(n
tPyz
n-tQу+t:z;t
tPx
рх
(t) dt.
1 J
o

502
Аналогично,
Гл.
18.
Развитие
теории
ДЛЯ
нескольких
лиц
nqxy; =
(ОО
Р(А
I
Т(у)
=
t]
tPy
J1,y(t)
dt =
(n
tqx
tPz
n-tqz+t
tPy
J1,y(t)
dt,
1
Jo
J
o
nqXy~
=
{ОО
P(AIT(z)=t]
tPz
JlZ(t)
dt = {n
tqx;tpzJlz(t)dt.
1
Jo
10
Второй
ИЗ
этих
интегралов
можно
выразить
в
терминах
вероятностей
первой
смерти
следующим
образом:
nqxy~
= {n
(1
- tPx)(tPz - nPz)
tPy
Jly(t) dt =
nq~z
-
nqx~z
- nPz(nqy - nqx;)'
1
10
Пример
18.5.3.
Используя
формулу
(18.4.1),
запишем
четыре
различных
ин
тегральных
выражения
для
nqwx~z,
предполагая,
что
продолжительности
предсто
12
ящей
жизни
взаимно
независимы.
Решение.
Здесь
А
=
{T(w)<T(x)<T(y)<T(z)
и
Т(у)<n}.
Тогда
nqwx~z
=
(n
tPxyz
n-tqx+t:y~t:z+t
tPw
Jlw(t) dt =
(n
tqw
tPyz
n-tqy~t:z+t
tPx
J1,x(t)
dt
12
J
o
1 J
o
=
(n
tqw;
tPz
tPy
Jly(t)
dt
=
(n
tqwx:
tPz
J1,z(t)
dt +nqwx: npz. (18.5.3)
Jo
Jo
1 1
Правая
часть
последнего
равенства
в
этой
цепочке
равенств,
полученная
при
усло
вии
на
С.В.
T(z),
включает
одно
слагаемое
для
T(z)
< n
и
одно
для
T(z)
>
n.
•
Применяя
равенство
(18.4.1)
в
примерах
этого
раздела
и
рассматривая
Р
(А
I
Т
=t),
мы
использовали
предположение
о
независимости
продолжительностей
предстоящей
жизни.
Теперь
рассмотрим
вычисление
этих
вероятностей,
если
интен
сивность
смертности
каждого
из
рассматриваемых
лиц
подчиняется
закону
Гомпер
ца.
Пример
18.5.4.
Покажем,
что
для
закона
Гомперца
з
1 1 1
ooqwxyz
=
ooqwxyz
ooqxyz
ooqyz
.
12
Решение.
Полагая
n
--+
00
в
формуле
(18.5.3),
получаем
ooqwx~z
=
{оо
tqw
tPyz
ooqy~t:z+t
tPx
J.Lx
(t) dt.
12
J
o
(18.5.4)
в
п.
(Ь)
примера
9.10.1
было
показано,
что,
согласно
закону
смертности
Гомперца,
(18.5.5)
где
с
ш
=
с
х
+
су.
Переписывая
это
выражение
для
данного
случая
и
подставляя
его
вместо
ooqy~t:z+t
В
подынтегральное
выражение
в
(18.5.4),
получим
{оо
c
y
+
t
су
(1
1
ooq1fg:~z
= J
o
c
y
+
t
+c
z
+
t
tqw
tPyz
tPx
J1,x(t)
dt =
су
+C
z
ooqxyz
-
ooQwxyz)'

18.6.
Еще
о
реверсивных
аннуитетах
503
Т(у)
~
Т(х),
Т(х)
<
Т(у)
~
Т(х)
+n,
Т(х)
+n
~
Т(у).
Формулу
(18.5.5)
можно
распространить
на
более
чем два
лица
и
затем
использовать
полученное
выражение.
Следовательно,
ooq
3 =
су
(
еЖ
_
еЖ
)
"ffYz
сУ
+e
Z
еЖ
+
сУ
+e
Z
C
W
+
еЖ
+
су
+c
Z
(
eW
) (
еЖ
) (
СУ)
1 1 1
= =
(ХЛ
WЖУZ
ооqжуz
ooqyz'
C
W
+
е
х
+
су
+e
Z
е
х
+
су
+e
Z
сУ
+e
Z
18.6.
Еще
о
реверсивных
аннуитетах
В
разд.
9.7
мы
исследовали
несколько
договоров
страхования
и
аннуитетов
для
групп,
состоящих
из
более
чем двух
лиц.
Хотя
там
рассматривались
более
общие
типы
реверсивных
аннуитетов,
они
строились
только
для
двух
лиц
и иногда
с
га
рантированным
периодом
выплат.
Рассмотрим
примеры
аннуитетов
с
гарантирован
ными
периодами
выплат,
которые
отсчитываются
от
момента
смерти,
и
примеры
аннуитетов,
начало
выплат
которых
связано
с
порядком
случаев
смерти.
Мы
также
ограничим
наше
обсуждение
непрерывными
аннуитетами.
Начнем
с
рассмотрения
двух
примеров
реверсивных
аннуитетов
с
гарантирован
ным
периодом
выплат,
исчисляемым
с
момента
смерти.
Для
реверсивного
аннуите
та,
по
которому
выплачивается
аннуитет
на
срок
n
лет
лицу
(у)
после
смерти
лица
(х),
гарантированный
период
выплат
является
отсроченным
статусом,
так
что
мы
возвращаемся
к
начальным
понятиям.
Настоящая
стоимость
выплат
Z
на
момент
заключения
договора
- это
{
О,
_
Т(х)-
Z - v
aT(y)-Т(х)l'
vT(x)(i
nJ,
Используя
формулу
(18.4.2)
при
условии
Т(х)
=t,
можно
записать
актуарную
на
стоящую
стоимость
в
виде
E[Z] =
100
E[Z
I
Т(х)
=
t]
,Рх
JLx
(t) dt =
100
tPy v
t
ау+Ыil
,Рх
JLx
(t)
dt.
Подставляя
выражение
-
J.t+n
B-t
ay+t:nJ
= t V
b-tРу+t
ds
в
формулу
(18.6.1),
получим
fooJ.t+n
E[Z]
=
Jo
t
VSsPytPxPx(t)dsdt.
Затем
поменяем
порядок
интегрирования,
так
что
E[Z]
= {n
{В
VS
вРу
(Рх
Ilx(t)
dtds
+
(ooJ.s
v
8
аРу
tРж
Рж(t)
dt ds
Jo
Jo
J
n
в-n
= 1
n
v·
.Ру(l
-
.Рх)
ds +
[00
V·
.py(.-nРх
-
.Рх)
ds
=
ау:nJ
-
аху
+V
n
пРу
а
ж
:
v
+
n
.
(18.6.1)
(18.6.2)

504
Гл.
18.
Развитие
теории
ДЛЯ
нескольких
лиц
Выражение
в
правой
части
второго
равенства
в
(18.6.2)
является
формулой
текущих
платежей
для
этой
актуарной
настоящей
стоимости.
Другим
реверсивным
аннуитетом
этого
типа
будет
аннуитет,
выплаты
которо
го
начинаются
спустя
n
лет после
смерти
лица
(х)
и
продолжаются
лишь
до
тех
пор,
пока
лицо
(у)
живо.
Настоящая
стоимость
выплат
Z,
рассчитанная
на
момент
заключения
договора,
составит
{
О,
Z =
Т(ж)+n
_
(v
)aT(y)-Т(ж>-nl'
Т(у)
~
Т(х)
+n,
Т(х)
+ n <
Т(у).
Используя
формулу
(18.4.2)
при
условии
Т(х)
= t,
актуарную
настоящую
стоимость
можно
записать
в
виде
Е[
Z]
=
100
Е[
Z I
т
(х)
=tJ,P.
JL.
(t) dt =
100
'+nРу
v'+n
ау+nн
,Р.
JL.
(t) dt . (18.6.3)
Подставим
1
00
t+n - _
в
t+nPy V ay+n+t - v
вРу
ds
t+n
в
(18.6.3)
и
получим
Е[
Z]
=
{ОО
(ОО
V
8
вРу
tРж
JLж
(t) dsdt.
Jo
Jt+n
Далее
поменяем
порядок
интегрирования,
так
что
{ОО
{в-n
(СО
E[Z] = J
n
Jo
V
S
s
РуtРжJ1ж(t)dtds=
Jn
VSspy(l-s_nрж)ds
=
Vnnpy(a
y
+
n
-
а
ж
:
у
+
n
)
=Vnnpy
ажl
у
+
n
'
(18.6.4)
Другой
класс
реверсивных
аннуитетов,
который
мы
рассмотрим,
возможно,
име
ет
ограниченный
коммерческий
интерес:
это
аннуитеты,
для
начала
выплат
которых
должно
произойти
некоторое
событие,
обусловленное
очередностью
смертей
в
груп
пе.
Рассмотрим
два
примера,
привлекая
начальные
понятия.
Пример
18.6.1.
Выразим
актуарную
настоящую
стоимость
реверсивного
анну
итета,
обозначаемую
через
a;Ylz'
(а)
согласно
определению,
(Ь)
в
форме
текущих
платежей,
изменив
порядок
интегрирования
в
результате
из
п.
(а).
Решение.
Используя
формулу
(18.4.2)
при
условии
Т(х)
=t,
получим
a;Ylz
=
100
v'
,Р.
JL.
(t)
'Ру
,Р.
ажн
dt
=
100
,Р.
JL.
(t)
'Ру
([00
v'
,Р.
ds)
dt
=
100
v'
,Р.
[1'
,Р.
JL.
(t)
'Ру
dtJds =
100
v'
,РжzЧ;у
ds. ,
Этот
результат
можно
рассматривать
как
актуарную
настоящую
стоимость
в
форме
текущих
платежей.
Он
показывает,
что
общий
вид
реверсивных
аннуитетов
можно
интерпретировать
достаточно
широко,
если
допускать,
что
потеря
статуса
(и)

18.7.
Нетто-премии
и
нетто-резервы
505
может
включать
некоторое
событие,
обусловленное
очередностью
смертей
в
группе.
В
общем
случае
имеем
a"l. =
100
v
t
tP.
tq" dt. (18.6.5)
Следующий
пример
демонстрирует
простой
частный
случай
для
двух
лиц,
в
котором
актуарная
настоящая
стоимость
может
быть
сведена
к
выражению,
в
котором
нет
интегралов.
Пример
18.6.2.
Выразим
актуарную
настоящую
стоимость
аннуитета,
обозна
чаемую
через
a.~;ffiIY'
в
виде,
не
использующем
интегралы.
Решение.
Согласно
(18.6.5),
имеем
-1
(СО
t 1 d
ax:ffil
y
=J
o
V
tPy
tQx:ffi
t
= 1
n
v'
tPy
[1
!
sP.It.(s)
ds] dt +
[""
v
t
tPy
[1
n
sP.It.(s)
ds] dt
=
1
n
v
t
tpy(1 -
tP.)
dt
+
(1
-
пР.)
[00
vttPy
dt
=
ау
-
a.y:iiI-
v
n
nр.уау+n.
,
18.7.
Нетто-премии
и
нетто-резервы
В
этом
разделе
мы
остановимся
на
нетто-премиях
и
нетто-резервах
для
рас
сматриваемых
в
этой
главе
типов
страховых
договоров.
Как
и
в
гл.
б,
нетто-премия
будет
определяться
согласно
принципу
эквивалентности.
Как
и
в
гл.
7,
нетто-резерв
будет
определяться
по
перспективному
методу
как
условное
математическое
ожи
дание
будущих
потерь
при
условии
дожития
до
момента,
в
который
рассчитывается
резерв.
Период
выплаты
премий
должен
оканчиваться
не
позднее
момента
наступления
страхового
случая,
а
для
договоров
страхования,
учитывающих
очередность
смер
тей,
не
позднее
момента,
когда
ясно,
что
никаких
страховых
выплат
производиться
не
будет.
Этот
период
может
оканчиваться
раньше
указанных
моментов.
При
рассмотрении
страховых
выплат
на
случай
первой
смерти
премии
выплачи
ваются
лишь
до
тех
пор,
пока
все
лица
живы.
Используя
принцип
эквивалентности,
получаем,
например,
{4} - 1
..
{4} _ - 1
-1..
_-1
Рхуа
ху
=
Аху,
10
Р
(А'ху':2OI)аху:I01
-
А.
ху
':2OI'
P(Axyz)axyZ - A
xyz
.
Для
страховых
выплат,
осуществляемых
в
случае
второй
или
одной
из
последую
щих
смертей,
возможен
не
единственный
период
выплаты
премиЙ.
Для
того
чтобы
минимизировать
нетто-премии,
которые
могут
назначаться
для
определенных
стра
ховых
выплат,
МЫ
используем
наиболее
длительный
период.
Следующий
пример
иллюстрирует
этот
процесс
для
нескольких
случаев.
Пример
18.7.1.
Используя
принцип
эквивалентности,
запишем
уравнение
для
следующих
нетто-
премий:
(а)
Р
ху
,
(Ь)
Р(А
ху
;)'
(с)
Р(А
wж
:
уz
),
(d)
P(Ax;z)'
(е)
P(Ax;z)'
1
Решение.
(а)
Р
ху
аху
=
Аху,
-
2..
2 - 2
(Ь)
P(AXyz)aXYZ
= A
xyz
,
(с)
p(Awx:yz)awx:yZ =A
wx
:
yz
,

506
Гл.
18.
Развитие
теории
ДЛЯ
нескольких
лиц
(d)
До
тех
пор,
пока
живы
лицо
(у)
и по
крайней
мере
одно
из
лиц
(х)
и
(z),
страховые
выплаты
еще
возможны.
Следовательно,
-
2··
- 2
P(Axyz)ay:xz
==
A
xyz
·
(е)
В
этом
случае
страховые
выплаты
возможны,
если
живы
все
лица
или
если
живы
только
лица
(у)
и
(z).
Таким
образом,
соответствующий
период
выплаты
премий
определяется
периодом
сохранения
статуса
(yz)
и
-
2..
- 2
P(Axy.Ja
yz
==
A
xyz
· •
1 1
Как
условное
математическое
ожидания
будущих
потерь
нетто-резерв
будет
за-
висеть от
условий
статуса,
используемого
в
расчетах.
Резерв
для
страховых
выплат
на
случай первой
смерти
определен
однозначно,
потому
что
все
лица
должны
до
жить
до
окончания
срока
действия
договора
страхования.
Проиллюстрируем
фор
мулы
резервов
для
двух
таких
договоров
страхования:
V
1
-А
1
_pl
..
5
'xy':IOl
-
'х+5:у+5':Ы
'ху':IOl
a
x
+
5
:
y
+
5
:51'
где
р
1..
А
1 V
1
А
1 p
1
..
'xy':I01
аху:IБJ
==
'ху':IOl'
5 xyz
==
x+5:y+5:z+5
- xyzax+5:y+5:z+5·
Для
страховых
выплат
на
случай
второй
или
одной
из
последующих
смертей
нетто
резерв
можно
рассчитать
как
условное
математическое
ожидание,
где
условие
со
стоит
либо
в
том,
(а)
какие
лица
дожили,
либо
в
том,
что
(Ь)
действие
договора
не
заканчивается
с
последней
смертью.
Рассмотрим
непрерывную
модель
страхования
со
страховой
выплатой
разме
ра
1
на
случай
потери
статуса
(ху)
и
с
премиями,
выплачиваемыми
до
наступления
второй
смерти.
Пусть
tL
-
будущие
потери
в
момент
времени
t.
В
зависимости
от
информации
о
том,
какое
из
лиц
(х),
(у)
(или
они
оба)
дожило
до
момента
времени
t,
имеем
или
E[t
L
I
Т(х)
>t n
Т(у)
>
t]
==
.A
x
+
t
:
y
+
t
- .P(.AXy)ax+t:y+t,
E[t
L
I
Т(х)
>t n
Т(у)
~
t]
==
.A
x
+
t
- .P(.AXy)ax+t
(18.7.1)
(18.7.2)
(18.7.4)
E[tL
I
Т(х)
~
t n
Т(у)
>
t]
==
.A
y
+
t
- .P(.Axy)ay+t.
(18.7.3)
С
другой
стороны,
если
известно
только,
что
статус
еще
не
потерян,
то
нетто
резерв
представляет
собой
величину
t V(.A
xy
)
==
E[t
L
I
Т(ху)
>t],
которую
можно
рассчитать
по
формуле
полной
вероятности
как
сумму
E[t
L
I
Т(х)
>t n
Т(у)
~
t]
Р[Т(х)
>t n
Т(у)
~
t I
Т(ху)
>
t]
+ E[t
L
I
Т(х)
~
t n
Т(у)
>
t]
Р[Т(х)
~
t n
Т(у)
>t I
Т(ху)
>
t]
+E[t
L
I
Т(х)
>t n
Т(у)
>
t]
Р[Т(х)
>t n
Т(у)
>t I
Т(ху)
>
t].
Б
этом
выражении
условные
математические
ожидания
задаются
формулами
(18.7.1), (18.7.2)
и
(18.7.3).
В
предположении
независимости
С.в.
Т(х) и
Т(у)
ве
роятности
примут
вид
Р[Т(х)
>t n
Т(у)
~
tI
Т(ху)
>
t]
= (
/Рж(l
(tP.)
) .
tPx 1 - tPy +tPy 1 - tPx +tPx tPy

18.8.
Замечания
и
литература
507
(18.7.8)
Комбинируя
эти
формулы,
получаем
,У(А
ху
)
=
(1
) +
~1
) +
{,рх(l-
'Ру)[А
хн
-
Р(А.у)а.+,]
tPx - tPy tPy -
tРж tРж
tPv
+
tpy(l
-
tрж)(А
у
+
t
-
Р{Ажу)ау+tJ
+
tРж
tpy[A
x
+
t
:
y
+
t
-
Р(А
жу
)
a
x
+
t
:
y
+
t
]}' (18.7.5)
Теперь
подставим
равенства
аху
=
аж
+
ау
-
аху,
Аху
=
Ах
+
Ау
-
А.
ху
,
полученные
в
разд.
9.7,
в
последний
член
формулы
(18.7.5),
стоящий
в
квадратных
скобках,
и
получим
tPx
tРу[А
ж
+
t
:
у
+
t
- P(Axy)ax+t:y+t)
= tPx
tpy[A
x
+
t
+Ay+
t
- A
x
+
t
:
y
+
t
-
Р(Аху){аж+t
+ay+t - ax+t:y+t)].
Подставляя
данный
результат
в
(18.7.5),
получим
tV(A
xy
) =
[(tPx
A
x
+
t
+ tPy A
y
+
t
-
tPx
tPy A
x
+
t
:
y
+
t
)
-
P(Axy)(tPx
ax+t +tPy ay+t - tPx tPy ax+t:y+t)]/(tPx +tPy - tPx tPy)· (18.7.6)
Так
как
(ху)
является
статусом
дожития,
он имеет
функцию
условного
дожи
тия
при
условии,
что
статус
сохраняется
до
момента
времени
t.
Обозначим
ее
через
uPx1i+t.
Нетто-резерв
по
договору
страхования,
обсуждавшемуся
выше,
можно
рас
считать
непосредственно,
исходя
из
функции
условного
дожития,
если
она
вычис
лена
заранее.
Более
точно,
uPx1i+t
=
Р[Т(ху)
>
и
+t I
Т{ху)
>
t]
=
t+uРж
+t+uPy - t+uPxy . (18.7.7)
tPx + tPy - tPxy
Подчеркнем,
что
лишь
при
t =
О
доподлинно
известно,
что
оба
лица
(х)
и
(у)
живы.
Если
предположить
независимость
продолжительностей
предстоящей
жизни
этих
лиц,
ТО
в
качестве
соответствующей
функции
плотности
условного
распределения
для
статуса
дожития
последнего
лица при
условии,
ЧТО
этот
статус
сохранится
до
момента
времени
t,
получим
u+tPx
J-tx(t
+
и)
+u+tPy
J-ty{t
+
и)
-
u+tPxy[J-tж(t
+
и)
+
J-ty(t
+
и)]
tPx +tPy -
tРжу
Если
каждый
из
сомножителей
u+tP
в
числителе
формул
(18.7.7)
и
(18.7.8)
можно
представить
в
виде
произведения,
например,
u+tPx = uPx+t tPx,
то
эти
выражения
будут
представлять
собой
взвешенные
средние
с
весами,
равными
вероятностям
до
жития
до
t.
Если для
расчета
величины
E[vT(xy)-t
-
Р(А.
ху
)aT(xy)-tll
Т(ху)
>
t]
используется
выражение
(18.7.8),
то
мы
вновь
получаем
равенство
(18.7.6).
18.8.
Замечания
и
литература
Практические
приложения
материала
этой
главы
не
так
многочисленны,
как
приложения
некоторых
других
глав.
Тем
не
менее
существует
обширная
актуарная
литература
по
различным
вопросам
теории
страхования
нескольких
лиц.
Главы
10,

508
Гл.
18.
Развитие теории
ДЛЯ
нескольких
лиц
11,
12
и
13
книги
[Jordan 1952]
и
гл.
7,8
книги
[Neill1977]
частично
посвящены
этим
вопросам.
Теорема
18.2.2
(см.
ниже)
-
одна
из
основных
теорем
теории
вероятностей.
Она
объединяет
многие
идеи
гл.
4
книги
[Feller 1968].
Метод,
используемый
в
доказатель
стве
результатов
этого
типа,
часто
называется
.методо.м
67Слю-ченuя
u
UС1Слю-ченuя.
Обзор
основных
результатов
в
этой
области
содержится
в
работе
[Takacs 1967],
при
чем
в
ней
приведена
обширная
библиография.
Варинг
дал
высокую
оценку
приложе
ниям
этих
алгебраических
методов к
расчету
величин
страховых
аннуитетов.
Ранее
актуарные
учебники
выводили
результаты
следствий
18.2.1
и
18.2.3
с
помощью
так
называемого
Z
-.метода.
Это
мнемоническое
правило,
основанное
на
наблюдении,
что
коэффициенты
при
tDj
в
выражениях
tPXl
...
[:l
и
tPXl
...
:1o
совпадают
с
соответ
ствующими
коэффициентами
в
разложениях
величин
zk/(l
+
Z)k+l
и
Zk/(l
+
Z)k.
Более
ранняя
версия
теоремы
18.2.2
содержится
в
обсуждении
работы
[White,
Greville 1959J,
проведенном
Шютте
и
Несбиттом.
Использование
этих
методов
для
определения
актуарной
настоящей
стоимости
доли
аннуитета,
выплачиваемого
до
момента
последней
смерти
в
группе
лиц
с
распределением
дохода
равными
доля
ми
среди
доживших,
является
предметом
упражнения
18.36
и
статьи
[Rasor, Myers
1952].
Другое
доказательство
теоремы
18.2.2,
не
содержащее
ссылок
на
теорию
ве
роятностей,
дано
в
работе
[Buchta 1994].
Некоторые
из
результатов,
касающихся
премий
и резервов
для
договоров
стра
хования
на
случай
последней
смерти
в
группе,
обсуждались
в
статье
[Frasier 1978].
В
договорах
страхования
на
случай
смерти
с
сохраненными
выплатами
часто
оговаривается
право
на
изменение
условий
договора
(страховой
опцион).
в
каждую
годовщину
заключения
договора
страхователь
имеет право
на
получение
выкуп
ной
суммы
и
заключение
нового
договора
страхования,
используя
доступную
на
тот
момент
времени
экономическую
и
медицинскую
информацию
с
целью
увеличения
актуарной
настоящей
стоимости
обязательств
по
договору
страхования.
Рейнольдс
в
работе
[Reynolds 1994]
обсуждает
расходы
на
реализацию
такого
права
по
догово
рам
на
случай
последней
смерти,
для
которых
премии,
резервы
и
выкупные
суммы
определяются
с
использованием
функций
условного
дожития,
подобных
(18.7.7).
Он
показал,
что
важно
учитывать
антиселекцию
рисков
смертности
в
том
смысле,
что
страхователи,
реализующие
право
на
изменение
условий
договора,
«здоровее~,
т. е.
имеют
большую
вероятность
прожить
долго,
чем
те,
кто
не
реализует
этого
права.
Учет
ожидаемых
дополнительных
расходов,
связанных
с
реализацией
этого
права,
должен
быть
встроен
в
дизайн
страхового
продукта.
Это
соображение
базируется
на
том,
что
выкупные
суммы,
как
и
резервы,
которые
получены
на
основе
функций
условного
дожития,
в
которых
фигурирует
лишь
сохранение
статуса,
как
правило,
будут
больше
соответствующих
величин,
рассчитанных
с
учетом
дополнительной
информации
о
дожитии
лиц
(х)
и
(у),
как
в
формулах
(18.7.1), (18.7.2)
и
(18.7.3).
Приложение
Теорема
18.2.2.
Пусть
А
1
,
А2,
...
,А
п
-
рассматриваемые
события,
и
пусть
р[л
обозншч.ает
вероятность
того,
'Что
происходит
ровно
j
из
этих
n
соб'ытиЙ.
Пусть
Dj
-
сумма
(по
всем
со'Четан.иям
по
j
соб'ытий
из
n)
вероятностей
того,
'Что
j
у?сазанн'ыlx
событий
произойдут,
вне
зависимости
от
того,
произойдут
ли
другие
n - j
событий.
~oгдa
для
лtoбого
набора
'Чисел
Со,Сl,
...
,сп
соР[о]
+
СIР[1]
+
С2Р[2]
+...+
сnр[п]
=
СО
+D
1
ilco
+D
2
il
2
со
+... +
Dnil
nсо.

Приложение
509
Доказательство.
Пусть
Xi
обозначает
индикатор
события
Ai,
так
что
Xi
= 1,
если
A
i
произошло,
и
X
i
=
О
В
противном
случае.
Пусть
}j
-
индикатор,
такой,
что
1j
= 1,
если
произошло
в
точности
j
из
n
событий
А
1
,
А
2
,
•••
,
А
п
,
и
}j
=
о
в
противном
случае.
Заметим,
что
математическое
ожидание
с.в.
1j
равно
P[j].
Наконец,
определим
оператор
ф(Е)
как
функцию
оператора
сдвига
Е
= 1 +
Д
по
формуле
ф(Е)
=
(Х1
Е
+1
-
Х
1
)(Х2
Е
+1
-
Х2)'
..
(Х
П
Е
+1
-
х
п
).
Заметим,
что
любой
сомножитель
равен
либо
Е,
если
входящая
в
него
величина
Xi
равна
1,
либо
1,
если
эта
величина
равна
О.
Умножая,
получаем
ф(Е)
=
У
О
+
У
1
Е
+У2
Е
2
+... +
У
П
Е
П
,
поскольку
в
этом
разложении
степень
оператора
Е
равна числу
тех
Xi,
которые
рав
ны
1.
Таким
образом,
показатель
степени
оператора
Е
равен
числу
произошедших
событий
А
1
,А
2
,А
з
,
...
,А
п
,
Поскольку
степень
оператора
сдвига
Ej
,
примененная
к
величине
Со,
дает
Cj
,
получим
ф(Е)со
=
соУо
+
С
1
У
1
+... +
спУ
п
,
И
тогда
математическое
ожидание
величины
ф(Е)со
представляет
собой
COPrO]
+
СI
Р
[l]
+... +
спР[п]·
Поскольку
Е
= 1 +
д,
можно
также
записать
ф(Е)
в
виде
ф(Е)
=
(1
+
х,LI.)(1
+
х,LI.)
...
(1
+
ХпLl.)
=1+t
(.
L .
Х"
Х;,
...
Х"
)
Ll.
j
,
}=1
Ч
,.2,··".;
где
коэффициент
при
дj
представлен
в
виде
суммы
всех
возможных
произведений
(в
ко
личестве
(;)
по
j
С.В.
Xi.
Поскольку
Xil
Xi2
...
Xij
= 1
лишь
в
случае,
если
произошло
со
бытие
A
i1
A
i2
...
Aij'
математическое
ожидание
с.в.
Xil
Xi2
...
Xij
равно
вероятности
P(A
i1
A
i2
...
A
ij
)
И
математическое
ожидание
случайной
величины
L
Xil
Xi2
...
Xij
i1,i2,
..
·.ij
равно
Dj.
Следовательно,
математическое
ожидание
с.в.
ф(Е)СQ
также
можно
записать
в
виде
Приравнивая
два
выражения
для
математического
ожидания
с.в.
ф(Е)со,
завершаем
дока
зательство
теоремы.
•
Обычная
теорема
сложения
вероятностей
дает
пример
применения
теоремы
18.2.2.
Для
n=4
Р(А
1
U
А
2
U
Аз
u
А
4
)
=
Р[1]
+
Р[2]
+
~З]
+P[4J.
Здесь
со
=
О
и
сl
=
С2
=
сз
=
С4
=1
в
первой
форме
записи
(*)
математического
ожидания
ф(Е)СQ.
Из
таблицы
i
Ci
дСi
д2
Сi
ДЗ
Сi
д4
Сi
О
О
1
-1
1
-1
1 1
О
О
О
2 1
О
О
3 1
О
4 1

510
Гл.
18.
Развитие
теории
для
нескольких
лиц
мы
видим,
что вторая
форма
записи
(**)
математического
ожидания
представляет
собой
P(A
1
U
А
2
U
Аз
u
А4)
= D
1
-
D2
+
Dз
-
п4
4
=L
P(Ai)
- L
P(AiAj)
i=1
по всем
комбинациям
по
два
из
1.
2,
3,
4
+
по
всем
комбина.циям
по
три
из
1,
2,
З,
4
Упражнения
Если
не
оговорено
противное,
продолжительность
жизни
всех
лиц
описывается
одной
и
той
же
таблицей
смертности,
а
случайные
величины
продолжительности
предстоящей
жизни
независимы.
к
разделу
18.2
18.1.
Опишите
события,
имеющие
вероятности,
заданные
следующими
выражениями:
(а)
tPwx
+
tPwy
+
tPwz
+
tPxy
+
tPxz
+
фу::
-
3(tpwxy
+
tpwxz
+
tpwyz
+
tPxyz)
+
7tpwxyz,
(Ь)
tpw
+
tpx
+tPII +
tPz
-
2(tpwx
+
tpwy
+
tpwz
+
tPxy
+
tPxz
+
tPyz)
+
4(tPwxy
+
еРшх::
+
tpwyz
+
tPxyz)
-
8tpwxyz.
[о]
_ 1 1
18.2.
Используя
следствия
из
разд.
18.2,
проверьте,
что
tPXIX2
...
Xm
- -
tPXIX2
...
Xrn
•
18.3.
Выдержка
из
таблицы
актуарных настоящих
стоимостей
аннуитетов,
сопряжен
ных
со
статусом
дожития
всех
лиц
из
группы
и
вычисленных
с
процентной
ставкой
3,5%,
выглядят
следующим
образом:
Статус
дожи-
Актуарная
настоящая
стоимость
аннуитета
постну
тия
всех
лиц
мерандо,
связанного
со
статусом
ДОЖИТИЯ
всех
лиц
20:26:28 14,4
20:26:29 14,3
20:28:29 14,0
26:28:29 13,8
20:26:28:29 12,5
(а)
Рассчитайте
актуарную
настоящую
стоимость
аннуитета,
выплачиваемого
в
конце
каждого
года
до
тех
пор,
пока
ровно
трое
из
лиц
(20), (26), (28)
и
(29)
живы.
(Ь)
Рассчитайте
актуарную
настоящую
стоимость
страховой
выплаты
размера
10000
в
конце
года
смерти
второго
лица
из
совокупности
лиц
(20), (26), (28)
и
(29).
В
2
[2]
D'
3 4
18.4.
ыразите
tP
wxyz
-
tP
wxyz
через
t
j,
J =
1,2,
, .
18.5.
Выразите
в
терминах
символов
аннуитетов
актуарную
настоящую
стоимость
аннуитета
с
выплатами
размера
1
в
конце
каждого
года
до
тех
пор,
пока
лицо
(w)
и
по
крайней
мере
одно
из
лиц
(х),
(у)
и
(z)
живы.
18.6.
Если
j..t4o(t)
=0,002,
О
~
t
~
10,
и
~
=0,05,
то
вычислите
величину
A40:40:40:40:40:IOl'
18.7.
Учреждается
фонд
доверительного
управления
имуществом
дЛЯ
обеспечения
до
хода
трем
лицам
(х),
(у)
и
(z).
Фонд
должен
обеспечивать
непрерывный
доход
с
годовой
суммой выплат
8
единиц
каждому
лицу,
пока
все
они
живы,
с
годовой
суммой
выплат
10
единиц
каждому,
если
живы
два
лица,
и
с
годовой
суммой выплат
15
единиц
единственному
оставшемуся
в
живых.
Рассчитайте
актуарную
настоящую
стоимость
(а)
всех
выплат,
которые
будут
сделаны,
(Ь)
всех
выплат
лицу
(х).
18.8.
Договор
страхования
обеспечивает
выплату
в
размере
4
единиц
после
первой
смерти
в
группе
из
четырех
лиц
возраста
х
лет,
в
размере
3
единиц
после
второй
смерти,
в
размере
2
единиц
после
третьей
смерти,
в
размере
1
единицы
после
четвертой
смерти.
Оцените
актуарную
настоящую
стоимость
выплат
по
этому
договору,
если
Ах
= 0,4
и
А.
хх
= 0,5.
