Бауэрс Н., Гербер Х., Джанс Д., Несбитт С., Хикман Дж. Актуарная математика
Подождите немного. Документ загружается.


Упражнения
381
(Ь)
при
т
~
00
последнее
слагаемое
в
правой
части
формулы
п.
(а)
сходится
к
aW
n
,
1-а
т(1
-
а)
-
а
+
а
т
+
1
а
-
а
т
+
1
(с)
E[Sn,m I
Wl
=Шl,
W2=W2,
...
,Wn
=ш
n
]
=
(1
_
а)2
J.t+
1 _
а
Ш
n
,
где
Е(Уn+l)
=
J.t.
к
разделу
13.3
13.3.
Предположим,
что
V
1
,
V2,
...
являются
независимыми
одинаково
распределенны
ми
случайными
величинами
с
общей
функцией
распределения
Р(
х)
и
функцией
плотности
f(x),
х
~
О.
Чему
равна
вероятность
того,
что
страховой
случай
произойдет
в
интервале
между
моментами
t
и
t +dt
при
условии,
что
N(t)
= i
и
Ti
= 8
(8
<
t)?
(Такое
обобщение
пуассоновского
процесса
называется
nроцессо.м.
восстановления).
13.4.
Пусть
{N(t),
t
~
О}
является
пуассоновским
процессом
с
параметром
А
и
pn(t) =
P[N(t)=n].
(а)
Покажите,
что
p~(t)
=
-лро(t),
p~(t)
=
-Apn(t)
+
ЛРn-l(t)
,
n
~
1.
(Ь)
ПредЛожите
интерпретацию
этой
формулы.
К
разделу
19.4
13.5.
Вычислите
lim8~O
R
и
lim8~oo
R.
13.6.
Воспользуйтесь
соотношением
е
ТХ
>
1+TX+~(Tx)2,
Т
>
О,
х
>
О,
чтобы
показать,
что
R <
26р}
/Р2.
13.7.
Предположим,
что
6 =
2/5
и
р(х)
=
~е-ЗХ
+
~e-7X,
х
>
О.
Вычислите
(а)
"
(Ь)
R.
13.8.
Предположим,
что
распределение
величины
страховых
выплат
дискретно
и
р(1)
=
1/4,
р(2)
=
3/4.
Подсчитайте
6,
если
R =
ln2.
13.9.
Покажите,
что
коэффициент
Лундберга
можно
получить
также
в
виде
един
ственного
решения
уравнения
/.00
erz[1 _
P(x)]dx
=
~,
т
<
т.
к
разделу
13.5
13.10.
Воспользуйтесь
теоремой
13.5.1
дЛя
вычисления
знаменателя
в
формуле
(13.4.4)
при
и
=
О.
Справедлив
ли
полученный
результат
для
(13.5.2)?
13.11.
(а)
Покажите,
интерпретируя
приведенное
ниже
равенство,
что
при
и
~
О
л
l
и
А
100
'Ф(и)
= -
[1
-
Р(у)J'Ф(u
-
у)
dy
+ -
[1
-
Р(у)]
dy.
с
о
с
u
[Указание.
Воспользуйтесь
теоремой
13.5.1.)
(Ь)
Уравнение
из
п.
(а)
называется
уравнением
восстановления.
[См.
упр.
13.3.]
Оно
является
интегральным
уравнением,
поскольку
устанавливает
соотношение
между
функ
циями,
в
которые
входят
интегралы.
Один
из
методов
поиска
решения
интегрального
урав
нения
-
преобразовать
его
в
интегро-дифференциал'Ьное
уравнение.
Покажите,
что
ф'(u)
=
Н
ф(u)
-
1."
ф(u
-
y)p(y)dy
-
[1
-
Р(U)]}.
13.12.
Подставьтев
(13.5.4)
равенство
МХ(Т)
=
1+Рlr+~Р2r2+~рзтЗ+
...
и
выведите
выражения
дЛя
(а)
E[L
1
],
(Ь)
E[L~],
(с)
D[Ll].
К
разделу
19.6
13.13.
(а)
Покажите,
что
дЛя
С.В.
N
из
равенства
(13.6.5)
E[N] = 1/8, D[N] =
(1
+8)/82.
(Ь)
Воспользуйтесь
результатом
упр.
13.12
и
выведите
выражения
дЛя
E[L]
и
D[L].
(Указание.
Полезными
окажутся
формулы
(13.6.5), (12.2.5)
и
(12.2.6)
с
Pl = E[L
1
],
D[X]
=
D[L
1
].
Иной
метод
основан
на
разложении
выражения
для
ML(r)
из
(13.6.4)
по
степеням
т.]

382
Гл.
13.
Модели
коллективных
рисков
на
длительном
интервале
времени
13.14.
Определите
производящую
функцию
моментов
с.в.
L,
если
размер
выплаты
по
любому
страховому
случаю
равен
2.
13.15.
При
определенных
предположениях
вероятность
разорения
выражается
фор
мулой
феи)
=
(О,3)е-
2и
+
(О,2)е-
4и
+
(О,1)е-
7и
,
и
~
О.
Подсчитайте
(
а)
О,
(Ь)
R.
13.16.
Каково
математическое
ожидание
величины
страховой
выплаты
по
одНОМУ
страховому
случаю,
определяемой
распределением
вида
(13.6.10)?
13.17.
Предположим,
что
л
=3,
с
=1
и
р(х)
=
jе-
3Ж
+
1з6
е-
бж
,
х
>
О.
Вычислите
или
приведите
выражения
для
(а)
Рl,
(Ь)
О,
(с)
Мх(т).
Найдите
(d)
выражения
для
правых
частей
формул
(13.6.9)
и
(13.6.12),
(е)
явную
формулу
для
Феи).
13.18.
Предположим,
что
л
=1,
с
=
10
и
р(х)
=
(9х/25)е-
3Х
/
5
,
х
>
О.
Вычислите
или
приведите
выражения
для
(а)
Рl,
(Ь)
О,
(с)
мх(т).
Найдите
(d)
выражения
для
правых
частей
формул
(13.6.9)
и
(13.6.12),
(е)
явную
формулу
для
ф(и).
13.19.
В
работе
Бикмана
[Beekman 1969]
и
в
обсуждении
ее
Бауэрсом
в
том
же
номере
журнала
на
с.
275-277
было
предложено
следующее
приближение
для
функции
распреде
ления
С.в.
L:
P(L
~
и)
'"
~I(и)
+
(1
-
~)G(u:
а,
fЗ),
где
I(x)
-
функция
распределения
константы
О,
т.
е.
вырожденная
функция
распределе
ния,
а
G(u:
а,
fЗ)
-
функция
распределения
гамма-распределения
с
параметрами
Q
и
13.
(а)
Определите
~,
Q
И
f3
так,
чтобы
они
равнялись
.сгустку»
вероятностной
массы
в
нуле
и
первым
двум
моментам
С.в.
L
соответственно.
См.
упр.
13.13(Ь).
(Ь)
Каково
будет
в
этом
случае
приближение
для
Феи),
и
~
О?
13.20.
Для
процесса
рискового
резерва
(1)
суммарные
страховые
выплаты
описыва
ются
сложным
пуассоновским
процессом
и
(2)
распределение
величины
страховых
выплат
является
смесью
n
показательных
распределений,
функция
распределения
которых
зада
ется
формулой
(13.6.10).
(а)
Покажите,
что
условное
распределение
С.в.
Ll
при
условии,
что
величина
рискового
резерва
упадет
ниже
начального
уровня,
является
смесью
тех
же
самых
n
показательных
распределений.
(Ь)
Определите
выражение
для
n
весов
этой
смеси
в
терминах
весов
и
параметров
распределения
страховых
выплат.
(с)
Определите
E[L
1
].
13.21.
Для
процесса
рискового
резерва
из
примера
13.6.2
определите
(а)
функцию
плотности
С.в.
Ll,
(Ь)
E[LIJ,
(с)
D[Ll].
Ко
всем
темам
гл.авы
13.22.
В
контексте
формулы
(13.2.1)
пусть
С.В.
Gi =
Ui
-
Ui-l
обозначает
доход
стра
ховщика
между
моментами
времени
i-1
и
i.
Предположим,
что
Gl,
G
2
,
•••
-
независимые
одинаково
распределенные
случайные
величины.
Предположим
далее,
что
u(х)
=
_е-ОХ,
Q >
О,
является
функцией
полезности
страховщика.
Покажите,
что
Е[U(U
n
+l)
IU
n
=
х)
~
u(х)
тогда
и
только
тогда,
когда
а
~
R.
Приведите
интерпретацию
этого
результата.
13.23.
Заменим
BpeMeHHbIe
единицы
таким
образом,
чтобы
новые
единицы
были
в
f
раз
больше
старых
(для
некоторого
f >
О).
Если
ё,
.х
и
-Феи,
t)
обозначают
характеристики
модели
в
терминах
новых
единиц,
то
(а)
Как
выражаются
эти
новые
характеристики
через
с,
л
и
феи,
t)?

Упражнения
383
(Ь)
Для
какого
f
выполнено
равенство
>.
= 1?
(Некоторые
авторы
называют
такие
единицы
оnерацuонн'Ым
временем.)
13.24.
Пусть
для
рассматриваемого
процесса
рискового
резерва
(1)
суммарные
страховые
выплаты
представляются
сложным
пуассоновским
процес-
сом,
(2)
величина
страховых
выплат
равномерно
распределена
на
интервале
(О,
10),
(3)
8 =0,05,
(4)
и
= 0,0,
(5)
С.в.
И(Т)
является
отрицательным
рисковым
резервом
в
момент
разорения,
(6)
с.в.
И(Т-)
является
величиной
рискового
резерва
непосредственно
перед
разорени
ем.
(Замечание.
и(т-)
-
Х
=
И(Т),
где
с.в.
Х
-
величина
страховой
выплаты
в
момент
разорения.
]
Определите
Е[И(Т-)
IT
<
00].
(Указание.
Случайные
величины
И(Т-)
и
IU(T)I
в
этом
упражнении
одинаково
распределены.
Чтобы
проверить
этот
факт,
см.
(Gerber, Shiu 1998,
formula (3.7)].
К
nрид.оженuю
13.25.
Предположим,
что
все
страховые
выплаты
имеют
величину
1.
(а)
Выпишите
уравнение
для
ф(u),
которое
соответствует
формуле
(13.А.14).
(Ь)
Решите
это
уравнение
при
О
~
и
~
1.

14
ПРИЛОЖЕНИЯ
ТЕОРИИ
РИСКА
14.1.
Введение
Главы
12
и
13
были
посвящены
модели
коллективных
рисков.
Эта
модель
осно
вывалась
на
предположениях,
что
множество
страховых
договоров
порождает
слу
чайное
число
страховых
случаев
в
каждый
временной
период
и
что
величина
выплат
по
каждому
страховому
случаю
случайна.
Для
того
чтобы
применять
эту
модель,
нам
необходима
информация
о
распределении
числа
страховых
случаев
и
о
распре
делении
величины
выплаты
по
отдельному
страховому
случаю.
Выбор
таких
рас
пределений
обсуждался
в
разд.
12.3,
и
в
настоящей
главе
будут
добавлены
лишь
некоторые замечания
по
поводу
распределения
числа
страховых
случаев.
Здесь
рас
пределение
величины
выплаты
по
отдельному
страховому
случаю
будет
иллюстри
роваться
на
примерах
четырех
различных
видов
страхования,
а
именно
огневого,
автомобильного,
на
случай
кратковременной
потери
трудоспособности
и
страхова
ния
расходов
на
лечение
в
стационаре.
Мы
обсудим
два
метода
приближения
модели
индивидуальных
рисков
для
неко
торого
страхового
портфеля
моделью
коллективных
рисков.
Для
коротких
времен
ных
интервалов
это
позволит
заменить
модель
индивидуальных
рисков
моделью
коллективных
рисков.
Понятие
перестрахования
на
базе
эксцедента
убыточности
для
некоторого
стра
хового
портфеля
исследуется
с
общих
позиций.
Методы
вычисления
распределения
суммарных
страховых
выплат,
изложенные
в
гл.
12,
дают
способ
вычисления
пере
страховочных
нетто-премий
по
договорам
перестрахования
эксцедента
убыточности.
Мы
остановимся
также
на
интерпретации
некоторой
формулы
для
дивидендов
по
групповому
страхованию
как
формулы
при
страховании
эксцедента
убыточности.
Мы
дадим
пример
анализа
договора
перестрахования
методами
гл.
12
и
13,
а
также
путем
сравнения
коэффициента
Лундберга,
который
связан
с
вероятностью
разорения,
с
величиной
E[LJ,
которая
скорее
характеризует
величину
дефицита
при
разорении.
Основная
цель
настоящей
главы
-
указать
различные
способы
применения
те
ории
риска
к
задачам
страхования.
14.2.
Распределение
величины
страховых
выплат
Для
того
чтобы
продемонстрировать
широту
спектра
приложений
моделей
те
ории
риска,
в
настоящем
разделе
представлены
четыре
специальных,
но
охватыва
ющих
широкую
область,
приложения.
Здесь
обсуждается
распределение
величины
индивидуальных
страховых
выплат.
Для
построения
модели
индивидуальных
рис
ков
эту
информацию можно
затем
дополнить
вероятностями
наступления
индиви
дуальных
страховых
случаев.
Для
построения
модели
коллективных
рисков
эту
же

14.2.
Распределение
величины
страховых
выплат
385
информацию
можно
дополнить
данными
о
распределении
числа
страховых
случаев,
порождаемых
коллективом
страхователей.
Приложения,
предлагаемые
в
настоящем
разделе,
могут
быть
использованы
страховой
компанией
при
работе
с
одним
из
ви
дов
страхования
или
с
группой
однородных
страховых
договоров.
Промышленная
компания
может
использовать
их
для
моделирования
своей
программы
управления
рисками.
Огневое
страхование.
В
этом
виде
страхования
страховым
событием
являет
ся
пожар
на
застрахованном
объекте,
повлекший
потери.
Поскольку
пожар
может
причинить
серьезный
ущерб,
большим
страховым
выплатам
необходимо
сопоставить
адекватную
вероятность
при
помощи
функции
распределения
Р(х).
В
актуарной
литературе
предлагались
некоторые
стандартные
распределения.
Три
из
них
при
ведены
в табл.
14.2.1.
Тот
факт,
что
для
распределения
Парето
среднее
существует,
лишь
если
а
> 1,
а
дисперсия
-
лишь
если
а
> 2,
свидетельствует
о
том,
что
это
распределение
имеет
большой
разброс
вероятностей.
О
распределениях
такого
типа
говорят,
что
они
имеют
тяжелые
хвост'Ы.
Таблица
14.2.1.
Типичные
распределения
страховых
выплат
Название
р(
х)
Среднее
Дисперсия
р(l
+ q) +
q(l
+
р)
_ 2pq
0'2
fЗ2
а{З
Логнормальное
Парето
Смесь
показательных
e-(ln
ж_m)2/(
2q
2)
xu..J2;
Х
>
О,
и>
О
ахо
х
а
+
1
'
Х
>
хо
>
О,
а
>
О
рае-аж
+
q{Зе-
f3ж
,
х
>
О,
0<
р
<
1,
q = 1 -
р,
а,
{З
>
о
ахо
0'-1
'
0'>1
(а
- 2)(0' -
1)2'
0'>2
Для
того
чтобы
применить
одно
из
этих
стандартных
распределений,
его
пара
метры
необходимо
оценить
по
выборке
величин
страховых
выплат.
КАСКО
в
автомобильном
страховании.
В
этом
виде
страхования
страхо
вым
событием
является
причинение
ущерба
застрахованному
автомобилю.
Диапа
зон
величины
страхОВЫХ
выплат
не
столь
велик,
как
в
огневом
страховании. Поэто
му
гамма-распределение
(12.3.17)
достаточно
хорошо
соответствует
статистической
информации
и
используется
в
качестве
распределения
величины
страховых
выплат.
Параметры
этого
распределения
могут
быть
оценены
по
выборке
страховых
выплат.
Страхование
на
случай потери
трудоспособности.
Этот
вид
страхования
предусматривает
выплаты
нетрудоспособным.
Обычно
определяется
nериод
отсро'Ч
?Си
момента
начала
выплат,
например,
семь
дней
с
момента
потери
трудоспособно
сти.
Период,
в
течение
которого
производятся
выплаты,
имеет
также
ограничения
сверху,
например,
это
могут
быть
13
недель
или
период
до
момента
наступления
пен
сионного
возраста.
Если
речь идет
о
группе
страхователей,
то
этот
вид
страхования
называется
груnnов'Ы,.м
страхова'Н:uем
с
еженедел'Ьн'Ы.Ми
возмещениями
или
груn
nOBbtM
долгосро'Ч'Н,ым
страхованием
на
слу'Чай
нетрудоспособности,
в
зависимости
от
продолжительности
периода
выплат.
Величина
выплат
в
каждый
период
одна
и
та
же;
стоимость
страхового
случая
p~BHa
этой
величине
выплат,
умноженной
на
число
периодов,
составляющих
время,
13
-
1855
386
Гл.
14.
Приложения
теории
риска
пока
длится
нетрудоспособность)
минус
период
отсрочки.
Пусть
С.в.
У
представляет
собой
число таких
периодов.
Распределение
С.в.
У
может
быть
оценено
по
стати
стике
страховых
случаев
и
представлено
в
виде
таблицы
типа
табл.
14.2.2.
Обра
тите
внимание
на
аналогию
между
функцией,
представленной
во
втором
столбце
табл.
14.2.2,
и
функцией
дожития,
обсуждавшейся
в
связи
с
таблицами
смертности
в
гл.
3.
В
рассматриваемом
случае
такую
функцию
принято
называть
функцией
дли
тельности.
Она
дает
вероятности
длительности
или
сохранения
нетрудоспособности
на
протяжении
указанного
периода.
Аналогично
тому)
как
функции
дожития
могут
применяться
для
нахождения
различных
вероятностей
дожития
и
смерти,
ФУН7\,'Ц'UU
длительности
могут
применяться
для
нахождения
различных
вероятностей,
свя
занных
с
длительностью
и
завершением
периода
нетрудоспособности.
Таблица
14.2.2.
Иллюстративные
распределения
с.в.
У
длительности
страхового
случая
при
групповом
страховании
с
еженедельным
возмещением
(максимальный
срок
выплат
13
недель,
период
отсрочки
7
дней)
Длительность
Длительность
страхового
страхового
случая
(в
днях)
Р(У>
у)
Р(У=у)
случая
(в
днях)
Р(У>у)
Р(У=у)
О
1,00000
24
0,43364 0,01295
1
0,96500
0,03500
25
0,42150 0,01214
2
0,93026
0,03474
26
0,40970 0,01180
3 0,89677
0)03349
27
0,39864 0,01106
4 0,86359 0,03318
28
0,38788 0,01076
5
0,83164
0,03195
31
0063611)
,
6
0,80004
0,03160
35 0,32427
7
0,76964
0,03040
38
0,04832
8 0,73962 0,03002
42
0,27595
9
0,71077 0,02885
45
0,03753
10 0,68376 0,02701
49 0,23842
11
0,65846 0,02530
52
0,02980
12
0,63476 0,02370
56 0,20862
13 0,61254 0,02222
59
0,02399
14
0,59171
0)02083
63
0,18463
15
0,57218 0,01953
66
0,01939
16
0,55387
0,01831
70
0,16524
17 0,53615
0,01772
73 0,01586
18
0,51953 0,01662
77
0,14938
19 0,50342 0,01611
80 0,01300
20
0,48832 0,01510
84 0,13638
21
0,47367 0,01465
87
0,01077
22
0,45993
0,01374
91
0,00000
0,12561
23
0,44659
0,01334
1,00000
в
применении
модели
коллективных
рисков
к
групповому
страхованию
на
слу
чай потери
трудоспособности
такого
типа,
как
рассматривается
в
табл.
14.2.2,
веро
ятность
Р
(N
=n)
интерпретируется
как
вероятность
того,
что
в
рассматриваемой
1)
Для
удобства
считалось,
что
страховые
случаи,
заканчивающиеся
в
следующую
за
данным
моментом
неделю,
заканчиваются
в
конце
третьего
дня
этой
недели.

14.2.
Распределение
величины
страховых
выплат
387
группе
в
период
действия
страхового
договора
окажутся
n
нетрудоспособных,
пе
риод нетрудоспособности
которых
длится
не
менее
семи
дней.
Если
выплаты
по
нетрудоспособности
составляют
с
единиц
в
день,
то
распреде
ление
величины
страховых
выплат
задается
соотношением
р(х)
=
Р(У
=
х/с),
х
=
с,2с,3с,
...
,28с,31с,
...
,87с,91с.
в
этом
страховании
на
коротком
интервале
времени
начисление
процента
не
учиты
Бается.
При
групповом
страховании
на
случай потери трудоспособности
для
распределе
ния
числа
нетрудоспособных,
срок
нетрудоспособности
которых
превышает
период
отсрочки,
часто
подходит
пуассоновское
распределение.
Математическое
ожидание
числа
нетрудоспособных
при
таком
распределении
часто
предполагается
пропорци
анальным
числу
лиц
в
группе.
В
следующем
примере
показано,
как
сложное
пуас
соновское
распределение
можно
использовать
для
моделирования
группового
стра
хования
на
случай
потери
трудоспособности
с
периодом
выплат
умеренной
длины.
Число
страховых
случаев,
возникающих
в
группе
в
течение
периода
фиксированной
длины,
и
длины
периодов
выплат
по
отдельным
страховым
случаям
предполагаются
Бзаимно
независимыми.
Пример
14.2.1.
Рассмотрим
договор
страхования
на
случай
потери
трудоспо
собности
для
группы
из
200
женщин,
каждой
из
которых
32
года.
Выплаты
произво
дятся
ежемесячно
в
размере
2000
каждая,
начинаются
через
три
месяца
после
даты
потери
трудоспособности
и
продолжаются,
пока
сохраняется
нетрудоспособность,
но
производятся
не
больше,
чем
21
раз.
Предположим,
что
для
S,
величины
суммарных
Быплат
для
всей
группы,
подходит
сложное
пуассоновское
распределение.
Для
коэффициента
потери
трудоспособности
и
распределения
величины
стра
ховых
выплат
мы
воспользуемся
выдержкой
из
таблицы
длительностей,
приведен
ной
ниже.
Это
часть
таблицы,
опубликованной
в
1987
г.
Группой
уполномоченных
по
долгосрочной
нетрудоспособности
(ГУ
ДН).
Рассматриваемая
выдержка
соответ
ствует
группе
из
1000
женщин
возраста
32
лет.
Таблица
строилась
в
детерминисти
ческом
контексте.
В
нашем
при
мере
мы
достаточно
обоснованно
считаем,
что
дан
ные
соответствуют
сложному
пуассоновскому
распределению,
и
заголовки
столбцов
относятся
к
С.в.
У
из
третьего
столбца,
определение
которой
приводилось
выше.
Коэффициент
потери
трудоспособности
в
пересчете
на
одно
лицо
обозначается
че
рез
.А32.
Определим
математическое
ожидание
и
дисперсию
С.в.
S.
Решение.
Величина
страховой
выплаты
обозначается
через
Х
= 2000
У,
У
=
1,2,
...
,21,
а
функция
вероятностей
С.в.
У
обозначается
через
р(у).
Обратим
вни
мание,
что
в
этой
постановке
игнорируются
проценты,
начисляемые
за
период
в
21
месяц.
Математическое
ожидание
числа
случаев
потери
трудоспособности,
дли
тельность
которых
превосходит
период
отсрочки,
для
группы
из
200
страхователей
равно
200
.АЗ2'
В
нашей
постановке
E[S]
=
200.АЗ2Е[Х]
=
(2000)(200).АЗ2Е[У],
D[S] =
200.АЗ2Е[х2]
=
(20002)(200).АЗ2Е[у2].
(14.2.1)
(14.2.2)

388
Гл.
14.
Приложения
теории
риска
Длительности
из
таблицы
ГУ
ДН
дЛЯ
женщин,
утративших
трудоспособность
в
32
года;
трехмесячный
период
отсрочки
(1) (2)
(3)
Количество
месяцев
с
момента
потери
трудоспособности
Число
выплат
у
1000
Л32
Р
(У
~
у)
3 1 2,6640
4 2
2АОО8
5 3 2,1343
6 4 1,9277
7 5 1,7664
8 6 1,6431
9 7 1,5442
10
8 1,4614
11
9 1,3898
12 10
1,3288
13
11
1,2767
14
12
1,2320
15
13
1,1926
16 14 1,1575
17
15
1,1261
18 16
1,0983
19
17 1,0735
20
18
1,0512
21
19 1,0308
22
20
1,0125
23
21
0,9961
24
22 0,9815
Эта
таблица
продолжается
до
25
лет
с
момента
потери
трудоспособности
Для
того
чтобы
выразить
моменты
с.в.
S
через
значения,
приведенные
в
таблице
длительностей,
мы
проводим
следующие
вычисления:
21
00
21
=
LLP(Y)
=
LP(Y~x).
х=1у=х
х=1
Подставляя
это
выражение
в
(14.2.1),
мы
получим
E[S]
=200
Л32Е[Х)
=
(2000)(200)ЛЗ2Е[У]
= 400(2,6640 +2,4008 +... +0,99610) = 12203,12.
Для
вычисления
дисперсии
суммарных
страховых
выплат для
группы
из
200
стра
хователей
нам
надо
проделать
шаг,
аналогичный
использованию
соотношения
т
=
L~l
1
в
предыдущих
рассуждениях.
Легко
проверить,
что
т
2
=
L~=l
(2х
- 1).
14.2.
Распределение
величины
страховых
выплат
Поэтому
21
00
21
= L
(2х
-
1)
L
Р(У)
= L
(2х
- 1
)Р(У
;?:
х).
ж=l
у=ж
ж=1
Подставляя
это
выражение
в
(14.2.2),
мы
получим
389
21
D[S]
=
(2000)2(200)Л32Е[у2]
= (800
000)(1000)Л32
L(2x
-
l)Р(У;?:
х)
ж=1
=800000(1(2,6640) +3(2,4008) +... +41(0,9961)] =(425,9808)(106). •
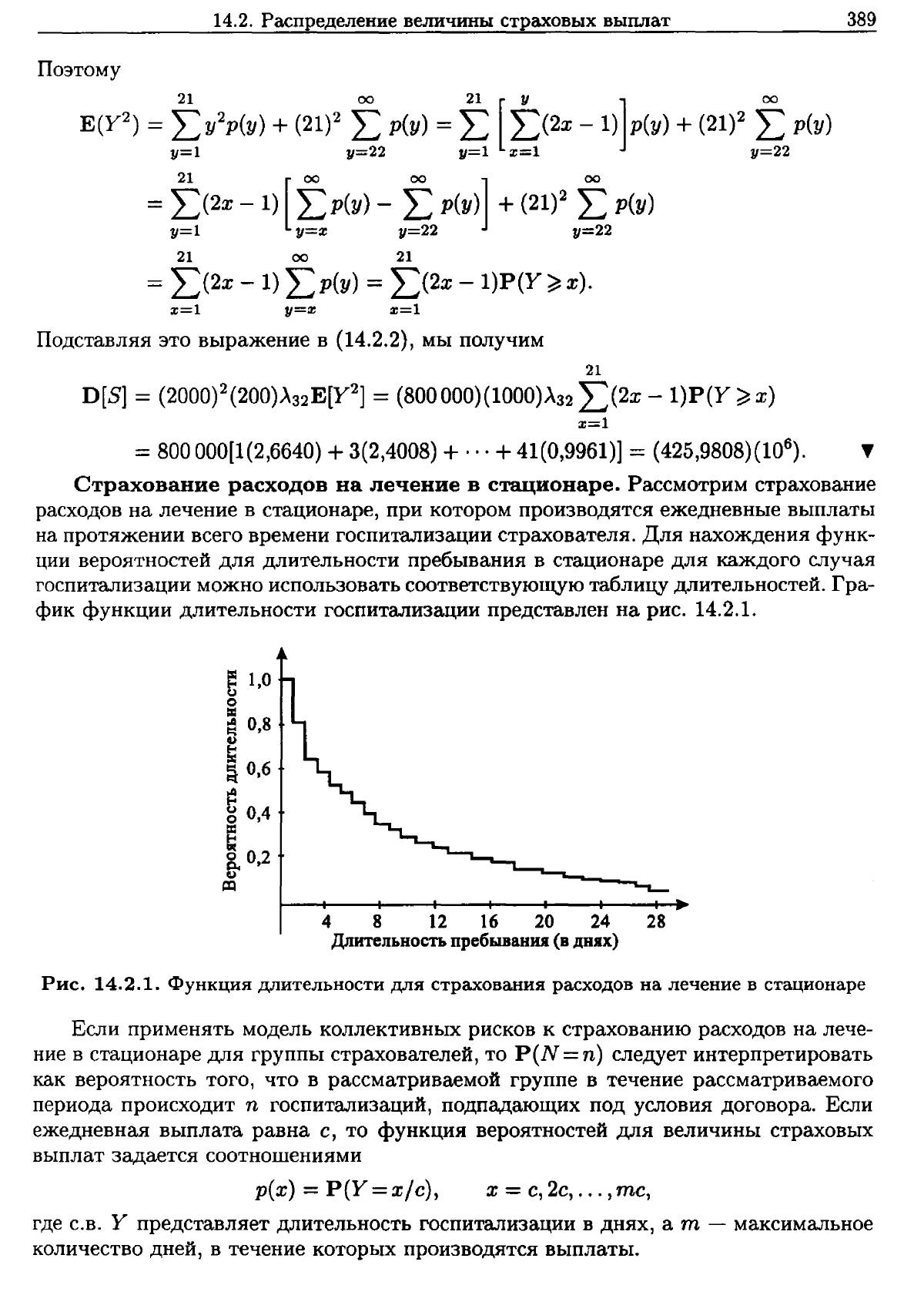
Страхование
расходов
на
лечение
в
стационаре.
Рассмотрим
страхование
расходов
на
лечение
в
стационаре,
при
котором
производятся
ежедневные
выплаты
на
протяжении
всего
времени
госпитализации
страхователя.
Для
нахождения
функ
ции
вероятностей
для
длительности
пребывания
в
стационаре
для
каждого
случая
госпитализации
можно
использовать
соответствуюшую
таблицу
длительностеЙ.
Гра
фИК
функции
длительности
госпитализации
представлен
на
рис.
14.2.1.
~
1,0
о
=
~
0,8
u
!;
~
0,6
~
~
0,4
~
&.
0,2
u
l::tI
4 8
12
16
20 24 28
Длительность
пребывания
(8
ДНJlХ)
Рис.
14.2.1.
Функция
длительности
для
страхования
расходов
на
лечение
в
стационаре
Если
применять
модель
коллективных
рисков
к
страхованию
расходов
на
лече
ние
в
стационаре
для группы
страхователей,
то
P(N
= n)
следует
интерпретировать
как
вероятность
того,
что
в
рассматриваемой
группе
в
течение
рассматриваемого
периода
происходит
n
госпитализаций,
подпадающих
под
условия
договора.
Если
ежедневная
выплата
равна
с,
ТО
функция
вероятностей
для
величины
страховых
выплат
задается
соотношениями
р(х)
=
Р(У
=х/с),
х
=
с,
2с,
...
,
тс,
где
с.в.
У
представляет
длительность
госпитализации
в
днях,
а
т
-
максимальное
количество
дней,
в
течение
которых
производятся
выплаты.

390
Гл.
14.
Приложения
теории
риска
Использование
моделей
теории
риска
в
перечисленных
приложениях
позволяет
оценить
величину
необходимой
суммарной
нетто-премии.
Эта
оценка
может
допол
няться
результатами
о
величине
разброса
потерь.
14.3.
Аппроксимация
индивидуальной
модели
Как
модель
индивидуальных,
так
и
модель
коллективных
рисков
призваны
от
разить
ключевые
аспекты
страховых
систем.
В
каждой
ИЗ
них
строится
распределе
ние
суммарных
страховых
выплат
в
рассматриваемых
страховых
системах.
В
этом
разделе
мы
излагаем
два
метода,
с
помощью
которых
сложное
пуассоновское
рас
пределение,
которое
обычно
ассоциируется
с
моделью
коллективных
рисков,
можно
использовать
для
аппроксимации
распределения
суммарных
страховых
выплат
в
модели
индивидуальных
рисков.
Мы
рассматриваем
модель
индивидуальных
рисков,
введенную
в
гл.
2,
примени
тельно
к
группе
из
n
страховых
договоров.
Суммарная
величина
страховых
выплат
в
течение
срока
действия
договоров
имеет
вид
S =
Х
1
+
Х
2
+ ... +
Х
n
,
где
через
X
j
обозначена
страховая
выплата
по
договору
с
номером
j
(j
=
1,2,
...
,n). Мы
различаем
наступление
страхового
случая и
величину
выплаты
по
нему
и будем
пользоваться
записью
(14.3.1)
Здесь
величина
l
j
равна
1,
если
по
договору
с
номером
j
произошел
страховой
случай,
и
О
в
противном
случае;
Bj
является
величиной
страховой
выплаты
по
этому
страховому
случаю
при
условии,
ЧТО
он
произошел.
При
условии,
ЧТО
С.в.
1
j
и
В
з
,
j = 1,2,
...
,
n,
являются
взаимно
независимыми,
n
Е[8]
= L qjJ.lj,
j=1
n n
D[S] = L
qj(1
- qj)J.lJ +L
qja;
з=1
j=1
(14.3.2)
(14.3.3)
(14.3.4)
[см.
(2.2.25)
и
(2.2.26)],
где
qj
обозначает
вероятность
того,
что
по
договору
с
номе
ром
j
произошел
страховой
случай,
J.lj
=
E[B
j
)
и
ау
=
D[B
j
).
Мы
обозначаем
функцию
распределения
с.в.
Bj
через
Pj(x).
Если
происходит
страховой
случай,
то
по
теореме
Байеса
вероятность
того,
что он
относится
к
дого
вору
с
номером
j
приблизительно
равна
qj/(ql
+
q2
+... +qn).
По
формуле
полной
вероятности
функция
распределения
выплаты
по
данному
страховому
случаю
при
близительно
равна
~
qjPj(X)
~
ql + ... +
qn
.
Далее
мы
рассмотрим
два
метода
приближения
распределения
С.в.
8
сложным
пуас
соновским
процессом.
В
первом
методе
используется
сложное
пуассоновское
распределение
с
пуассо
новским
параметром
(14.3.5)
