Бауэрс Н., Гербер Х., Джанс Д., Несбитт С., Хикман Дж. Актуарная математика
Подождите немного. Документ загружается.


13.3.
Модель
с
непрерывным
временем
361
13.3.
Модель
с
непрерывным
временем
Мы
переходим
к
построению
модели
разорения,
используя
два
случайных
про
цесса
с
непрерывным
временем,
процесс
числа
страховых
случаев
и
процесс
суммар
ных
страховых
выплат.
Для
моделирования
первого
мы
обычно
привлекаем
пуассо
новский
процесс,
а
для
моделирования
второго
-
сложный
пуассоновский
процесс.
Для
некоторого
страхового
портфеля
обозначим
через
N(t)
число
страховых
случаев,
а
через
S(t) -
суммарные
страховые
выплаты,
произведенные
до
момента
t.
Мы
начинаем
отсчет
с
момента
О;
таким
образом,
N(O) =
О.
Кроме
того,
S(t) =
О
ДО
того
момента,
пока
N(t)
=
О.
Как
и
в
гл.
12,
мы
обозначаем
через
X
i
величину
i-й
страховой
выплаты.
Тогда
S(t) = X
1
+
Х
2
+
Х
з
+... +
XN(t).
(13.3.1)
Процесс
{N(t),
t
~
О}
называется
nро'Цессо.м
'Чuсл,а
страХО8'ЫХ
слу'Чае6,
а
процесс
{S(t), t
~
О}
-
nро'Цессо.м
су.м.мар'Н'Ых
страХО6'ЫХ
6'Ыnлаm.
Эти
наборы
случайных
величин
называются
процессами,
и
нас
интересуют
их
совместные
распределения
во
все
моменты
времени
t
~
О,
в
отличие
от
гл.
12,
где
мы
интересовались
числом
страховых
случаев
и
суммарными
страховыми
выплатами
лишь
для
одного
момента
времени.
Пусть
t
~
О
и
h >
О.
Из
определения
следует,
что
разность
N
(t
+h) - N (t)
явля
ется
числом
страховых
случаев,
а
разность
S(t+h)
-S(t)
-
суммарными
страховыми
выплатами,
которые
происходят
в
интервале
между
t
и
t + h.
Пусть
T
i
обозначает
момент
времени,
когда
происходит
i-й
страховой
случай.
Тогда
Т
1
,
Т
2
,
..•
-
случай
ные
величины,
причем для
того,
чтобы
исключить
возможность
возникновения
од
новременно
двух
и
более
страховых
случаев,
будем
считать,
что
T
1
<
Т
2
<
Тз
<
....
Время,
прошедшее
между
двумя
последовательными
страховыми
случаями,
обозна
чается
через
i >
1.
(13.3.2)
Типичные
реализации
процесса
числа
страховых
случаев и
процесса
суммарных
страховых
выплат
показаны
на
рис.
13.3.1
и
13.3.2.
Заметим,
что
N(t)
и
S(t)
явля
ются
возрастающими
ступенчатыми
функциями,
такими,
что
скачки
происходят
в
моменты
времени
T
i
,
когда
наступают
страховые
случаи,
а
величины
скачков
рав
ны
1
для
процесса
N(t)
и
X
i
для
процесса
S(t).
N(t)
4
3
2
1
•
•
о
Т
1
Т
2
Тз
14
-
JIi
....
~
.....
_-
~-Vз·
......
----
~
----
..
t
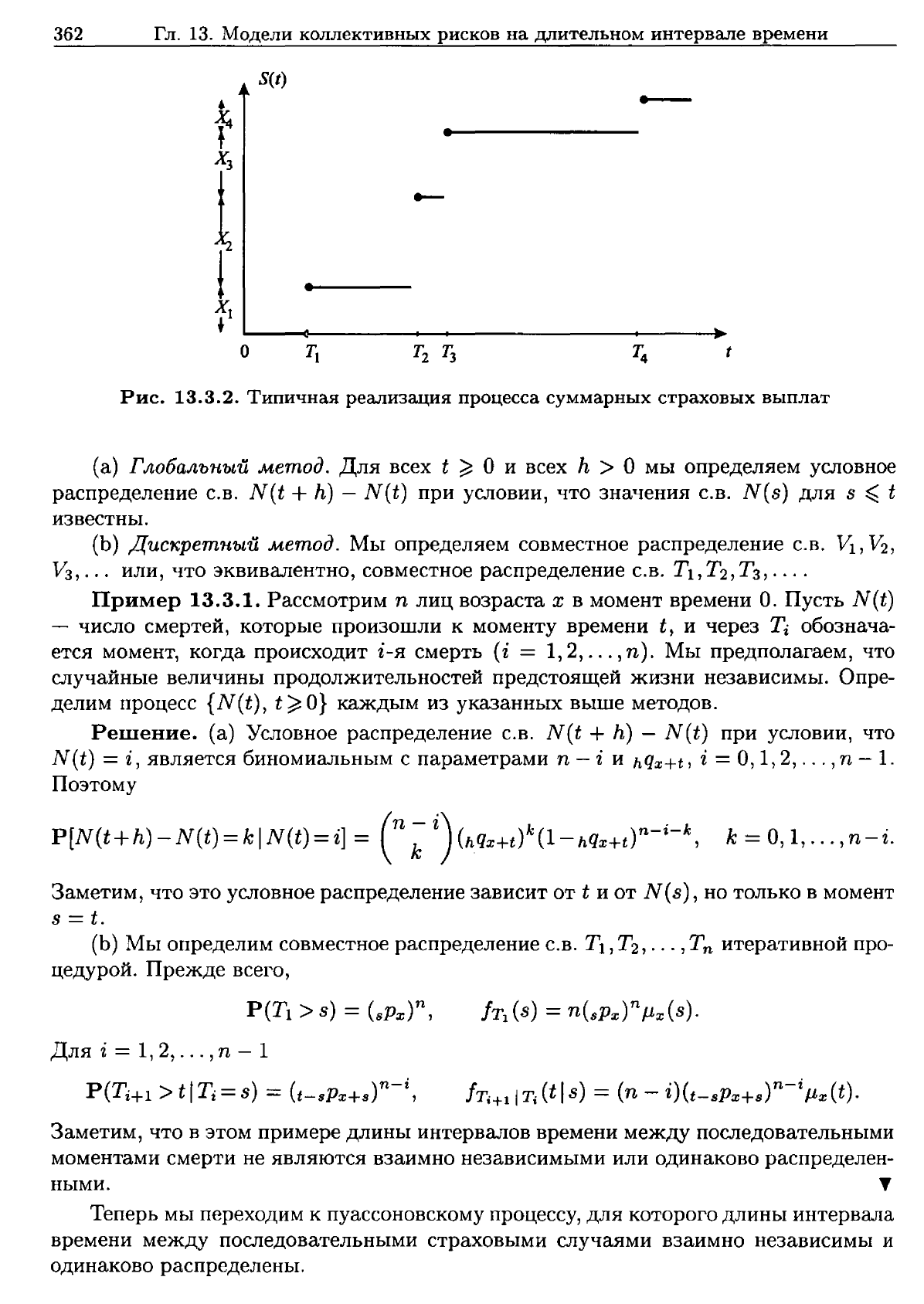
Рис.
13.3.1.
Типичная
реализация
процесс
а
числа
страховых
случаев
Имеется
несколько
способов
определять
распределение
процесса
числа
страхо
вых
случаев.
Мы
рассмотрим
два
из
них:
362
Гл.
13.
Модели
коллективных
рисков
на
дЛительном
интервале
времени
S(t)
•
•
f
•
Х
з
•
Х
!
~
О
Т
!
Т
2
13
Т
4
t
Рис.
13.3.2.
Типичная
реализация
процесс
а
суммарных
страховых
выплат
(а)
Глобал'Ь'Н.'ыU
метод.
Для
всех
t
~
О и
всех
h >
О
мы
определяем
условное
распределение
С.в.
N(t
+ h) -
N(t)
при
условии,
что
значения
с.в.
N(s)
для
s
~
t
известны.
(Ь)
Дискретный
метод.
Мы
определяем
совместное
распределение
с.в.
Vi,
V
2
,
V
З
,
•
••
или,
что
эквивалентно,
совместное
распределение
С.в.
Т
1
,
Т
2
,
ТЗ,
....
Пример
13.3.1.
Рассмотрим
n
лиц
возраста
х
в
момент
времени
О.
Пусть
N(t)
-
число
смертей,
которые
произошли
к
моменту
времени
t,
и
через
T
i
обознача
ется
момент,
когда
происходит
i-я
смерть
(i
=
1,2,
...
,
n).
Мы
предполагаем,
что
случайные
величины
продолжительностей
предстоящей
жизни
независимы.
Опре
делим
процесс
{N(t),
t
~
О}
каждым
из
указанных
выше
методов.
Решение.
(а)
Условное
распределение
С.в.
N(t
+ h) -
N(t)
при
условии,
что
N(t)
=
i,
является
биномиальным
с
параметрами
n - i
и
hQx+t, i =
0,1,2,
...
,n - 1.
Поэтому
P[N{t+h)-N{t)=kIN{t)=i]
=
(n
k
i){hqx+t)k{l-hqх+t)П-i-k,
k=O,l,
...
,n-i.
Заметим,
что
это
условное
распределение
зависит
от
t
и от
N
(в),
но только
в
момент
s =t.
(Ь)
Мы
определим
совместное
распределение
С.в.
Т
1
,
Т
2
,
•••
,
Т
N
итеративной
про
цедуроЙ.
Прежде
всего,
Для
i =
1,2,
...
,n-1
P(T
i
+
1
>t IT
i
=
s)
=
(t_spx+s)n-i,
Заметим,
что
в
этом
примере
длины
интервалов
времени
между
последовательными
моментами
смерти
не
являются
взаимно
независимыми
или
одинаково
распределен
ными.
~
Теперь
мы
переходим
к
пуассоновскому
процессу,
для
которого
длины
интервала
времени
между
последовательными
страховыми
случаями
взаимно
независимы
и
одинаково
распределены.

13.3.
Модель
с
непрерывным
временем
363
в
глобалыюм,
м,етоде
определения
nуассоновс'Х:ого
nроцесса
исходят
из
того,
что
P[N(t
+ h) -
N(t)
= kIN(s)
для
всех
s
~
tJ
e->'h(>
..
h)k
=
k!
для
всех
t
;:::
О
и
h >
О,
k =
0,1,2,3.
. . . (13.3.3)
Из
этого
определения
пуассоновского
процесса
вытекают
следующие
свойства:
(i)
Прuращен:u.я
стационарнu;
это
означает,
что
распределение
С.в.
N(t
+
h)
-
N(t),
которая
является
пуассоновской
с
параметром
)"h,
зависит
от
длины
h
интер
вала,
но
не
от
его
местоположения,
которое
определяется
величиной
t.
(ii)
Для
любого
множества
непересекающихся
временных
интервалов
nр'Uраще
1ШЯ
nезавuс'U.м:ы.,
т.
е.
для
t
l
< t
l
+ h
l
<
t2
<
t2
+ h
2
<
tз
...
< t
n
+ h
n
приращения
N(tl + h
l
) -
N(tl),
N(t2 + h
2
) -
N(t2),""
N(t
n
+ h
n
) -
N(t
n
)
взаимно
независимы.
(Ш)
Вероятnост'Ь
того,
'Что
nес1СОЛ'Ь7СО
страховых
слу'Чаев
nро'Uзойдет
одновре-
менно,
равна
НУЛЮ,
т.
е.
1
.
P(N(t
+
h)
-
N(t)
>
1]
1 -
e->'h
-
)"he->'h
1т
=
Нт
=
о.
h~O
h
h~O
h
В
дисх:ретном,
м,етоде
определения
nуассоновС7Сого
nроцесса
исходят
из
того,
что
интервалы
между
страховыми
случаями
V
l
, V
2
, V
з
,
.
..
взаимно
независимы
и
каждый
ИЗ
них
имеет
показательное
распределение
с
параметром
).,.
Покажем
эквивалентность
этих
двух
определений
пуассоновского
процесса.
Для
того
чтобы
показать,
что
процесс,
определенный
глобальным
методом,
обладает
ха
рактеристическим
свойством
процесса,
определенного
дискретным
методом,
заме
ТИМ,
что
P(Vi+l
>hIV
l
,
V
2
,
...
,
Vi)
=
р[уон
>h
IN(s)
ДЛЯ
всех
s
~
t =
tV;]
J=1
=
P[N(t
+h) -
N(t)
=
О
I
N(s),
s
~
t]
=
e->'h,
(13.3.4)
а
это
-
функция
дожития
для
каждой
С.в.
vi
В
рассматриваемом
пуассоновском
процессе.
Для
того
чтобы
показать,
что
процесс,
определенный
дискретным
методом,
об
ладает
характеристическим
свойством
процесса,
определенного
глобальным
мето
дом,
воспользуемся
определениями
с.в.
N(t),
T
j
, Vj,
их
взаимной
независимостью
и
свойствами
показательного
распределения
С.в.
vj
для
проверки
того,
что
P(N(t
+h) -
N(t)
=kI
N(s)
для
s
~
tJ
= P(Tk
~
h
и
Tk
+
Vk+l
>
hJ.
(13.3.5)
Поскольку
Tk
=V
l
+
V2
+
...
+
Vk
и
с.в.
vi
независимы,
одинаково
распределены
и
име
ют
показательное
распределение
с
параметром
)."
с.в.
Tk
имеет
гамма-распределение
с
параметрами
k
и
>...
Поэтому
соотношение
(13.3.5)
эквивалентно
соотношению
foh
P(Tk +V
H
! >h IT
k
=
U)!т.
(и)
du
=
foh
P(V
H
! >h -
u)!т.
(и)
du
_r
h
-.>.(h-u)
>..k
u
k-l
e
->'u
d _
e->'h
>..k
r
h
k-l
d _
->'h
(>"h)k
-
Jo
е
(k _
1)!
и
- (k _
1)!
Jo
и
и
-
е
k!'
правая
часть
которого
-
функция
вероятностей
числа
страховых
случаев
в
периоде
длины
h
для
пуассоновского
процесса.

364
Гл.
13.
Модели
коллективных
рисков
на
дЛительном
интервале
времени
Перейдем
к
определению
сложного
пуассоновского
процесс
а
в
рассматриваемом
нами
контексте.
Если
для
С.в.
S(t),
определенной
равенством
(13.3.1),
случайные
ве
личины
Х
1
,
Х
2
,
Х
З
,
•••
независимы,
одинаково
распределены
и
имеют
общую
функ
цию
распределения
Р(х)
и
если
они
также
независимы
от
процесса
{N(t),
t
~
О},
который
предполагается
пуассоновским,
то
процесс
{S(t), t
~
О}
называется
слож
НЫМ
nуассон.овС'l(;и,м,
nроцессо,м,.
Если
процесс,
описывающий
суммарные
страховые
выплаты,
является
слож
ным
пуассоновским
процессом
с
параметром
А
и
с
функцией
распределения
Р(х),
то
свойствам
соответствующего
процесса
N (t)
числа
страховых
случаев
отвечают
следующие
свойства
процесса
S(t) :
(а)
Если
t
~
О
и
h >
О,
то
распределение
С.в.
S(t +
h)
- S(t)
является
сложным
пуассоновским
С
параметром
>"h
и
с
функцией
распределения
Р(х),
т.
е.
00
p*k(x)
P[S(t
+
h)
- S(t)
~
х
IS(8)
дЛЯ
всех
s
~
t]
= L e->-'h(>
..
h)k
k!
'
k=O
где
p*k(x)
является
k-кратной
сверткой
функции
распределения
Р(х).
(Ь)
В
любой
момент
t
вероятность
того,
что
следующий
страховой
случай
про
изойдет
между
моментами
t +h
и
t +h +dh
и
что
величина
страховых
выплат
не
будет
превосходить
х,
равна
е
-
>-'h
(>..
dh)
Р
(х
)•
(с)
Процесс
{S(t), t
~
О}
является
процессом
с
независимыми
и
стационарными
приращениями.
То
есть
суммарные
выплаты
на
непересекающихся
временных
ин
тервалах
являются
независимыми
случайными
величинами
и
распределение
каждой
такой
величины
зависит
только
от
длины
соответствующего
временного
интервала,
а не
от
его
местоположения.
(d)
Если
через
S(t)
обозначается
сложный
пуассоновский
процесс
и
значение
t
фиксировано,
то
С.в.
S(t)
имеет
сложное
пуассоновское
распределение
с
пуассонов
ским
параметром
>"t.
Формулы
(12.3.2)
и
(12.3.3)
определяют
среднее
и
дисперсию
с.в.
S(t):
E[S(t)] =
>..tPl,
D[S(t)] =
>..tP2'
(13.3.6)
(13.3.7)
13.4.
Вероятности
разорения
и
распределение
страховых
выплат
Для
исследования
процесс
а
рискового
резерва
{U(t), t
~
О}
можно
пользоваться
его
связью
с
процессом
суммарных
страховых
выплат
S(t),
которая
выражена
соот
ношением
(13.1.1).
Всюду
далее
в
настоящей
главе
мы
будем
предполагать,
что
S(t)
является
сложным
пуассоновским
процессом.
При
этом
предположении
мы
сможем
найти
верхнюю
и
нижнюю
границы
для
ф(и).
В
частном
случае
показательного
распределения
индивидуальных
страховых
выплат
мы
укажем
явное
выражение
для
ф(U).
Прежде
всего
мы
предположим,
что
интенсивность
сбора
страховых
премий
с
превышает
ожидаемые
страховые
выплаты
в
единицу
времени,
что
составляет
ЛРl'
Далее,
определим
относительную
рисковую
надбавку
8
равенством
с
=
(1
+
8)>"Рl,
где
величина
В
положительна.
Легко
видеть,
что
если
В
=
О
или
В
<
О,
то
ф(и)
=
1,
т.
е.
разорение
произойдет
непременно.
13.4.
Вероятности
разорения и
распределение
страховых
выплат
365
Далее,
пусть
(-00,
'У)
обозначает
наибольший
открытый
интервал,
для
которо
го
существует
ПРОИЗВОДЯII~ая
функция
моментов
распределения
Р(х).
Мы
предпо
ложим,
что
величина
'У
положительна.
В
случае
показательного
распределения
с
параметром
(3
число
"у
равняется
(3,
а
для любого
распределения,
для
которого
ве
личина
страховых
выплат
ограничена,
число
'У
равно
+00.
Далее,
мы
предположим,
что
мх(т)
стремится
к
+00
при
r
~
'У.
Тот
факт,
что
это
предположение
для
ко
нечных'У
не
всегда
выполняется,
иллюстрируется
обратным
гауссовским
распреде
лением
в
примере
13.4.3.
Сравнение
рисунков,
которые
приводятся
в
этом
примере,
с
рис.
13.4.1
показывает
важность
этого
предположения.
1+
(l
+
е)р,
r
1
о
R
r
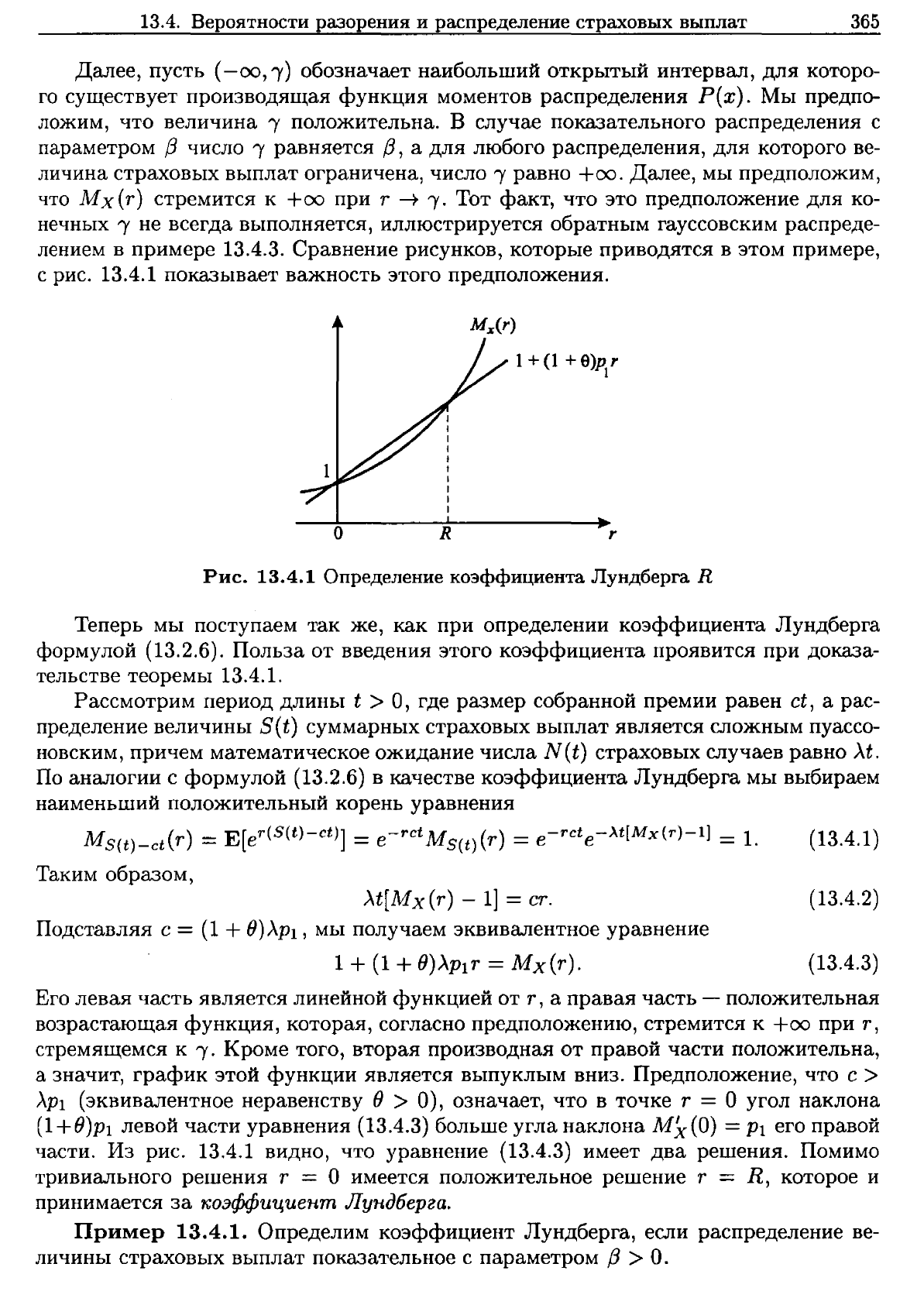
Рис.
13.4.1
Определение
коэффициента
Лундберга
R
Теперь
мы
поступаем
так
же,
как
при
определении
коэффициента
Лундберга
формулой
(13.2.6).
Польза
от
введения
этого
коэффициента
проявится
при
доказа
тельстве
теоремы
13.4.1.
Рассмотрим
период
длины
t >
О,
где
размер
собранной
премии
равен
ct,
а
рас
пределение
величины
S(t)
суммарных
страховых
выплат
является
сложным
пуассо
новским,
причем
математическое
ожидание
числа
N(t)
страховых
случаев
равно
Лt.
По
аналогии
с
формулой
(13.2.6)
в
качестве
коэффициента
Лундберга
мы
выбираем
наименьший
положительный
корень
уравнения
Ms(t)_ct(r)
=
E[er(S(t)-сt)]
=
e-rсtМs(t)(r)
=
e-
rсt
е--Хt[Мх(r)-1]
=
1.
(13.4.1)
Таким
образом,
лt[Мх(r)
-
1]
=
ст.
Подставляя
с
=
(1
+
В)ЛР1,
мы
получаем
эквивалентное
уравнение
1+
(1
+
В)ЛР1r
=
Мх(Т).
(13.4.2)
(13.4.3)
Его
левая
часть
является
линейной
функцией
от
т,
а
правая
часть
-
положительная
возрастающая
функция,
которая,
согласно
предположению,
стремится к
+00
при
т,
стремящемся
к
'У.
Кроме
того,
вторая
производная
от
правой
части
положительна,
а
значит,
график
этой
функции
является
выпуклым
вниз.
Предположение,
что
с>
ЛР1
(эквивалентное
неравенству
В
>
О),
означает,
что
в
точке
r =
О
угол
наклона
(1+В)Р1
левой
части
уравнения
(13.4.3)
больше
угла
наклона
M~(O)
=
Рl
его
правой
части.
Из
рис.
13.4.1
видно,
что
уравнение
(13.4.3)
имеет
два
решения.
Помимо
тривиального
решения
r =
О
имеется
положительное
решение
r = R,
которое
и
принимается
за
7'Ьоэффu:цuе'Н,m
Лун.дберга.
Пример
13.4.1.
Определим
коэффициент
Лундберга,
если
распределение
ве
личины
страховых
выплат
показательное
с
параметром
f3
>
О.

366
Гл.
13.
Модели
коллективных
рисков
на
дЛительном
интервале
времени
Решение.
Коэффициент
Лундберга
определяется
из
уравнения
(13.4.3),
которое
в
нашем
примере
имеет
вид
1
(1
+
8)т
_
/3
+
/3
-
/3-т'
или,
в
форме
квадратного
уравнения
по
т,
(1
+
8)т
2
-
8/3т
=
О.
Как
и
ожидалось,
r =
О
является
решением,
а
наименьшим
положительным
реше
нием,
которое
и
является
коэффициентом
Лундберга,
оказывается
R =
8/3
.
1+8
Пример
13.4.2.
Вычислим
коэффициент
Лундберга,
если
все
величины
стра
ховых
выплат
равны
1.
Решение.
В
силу
формулы
(13.4.3)
коэффициент
Лундберга
есть
положитель
ный
корень
уравнения
1 +
(1
+
8)т
=
е
Т
•
Результаты
численных
расчетов
для
приведенного
выше
уравнения
и
нескольких
выбранных
значений
В
приводятся
ниже:
()
R
В
R
0,2 0,35420 1,0 1,25643
0,4 0,63903 1,2 1,41318
0,6 0,87640
1,4
1,55368
0,8 1,07941
У
в
общем
случае
коэффициент
Лундберга
является
возрастающей
функцией
от
носительной
рисковой
надбавки
В.
В
этом
легко
убедиться,
взглянув
на
рис.
13.4.1.
При
росте
В
угол
наклона
прямой,
проходящей
через
точку
(0,1),
увеличивается,
так
что
точка
пересечения
этой
прямой
и
рассматриваемого
графика
смещается
вправо
и
вверх.
Пример
13.4.3.
Предположим,
что
распределение
величины
страховых
выплат
гауссовское
с
параметрами
о:
и
/3.
Для
этого
случая
(а)
определим
наибольший
открытый
интервал
(-00,
'"'(),
на
котором
определена
производящая
функция
моментов
М
х
(t) ,
(Ь)
определим
предел
функции
М
х
(t)
при
t
-+
'"'(,
(с)
выпишем
уравнение
для
коэффициента
Лундберга,
(d)
нарисуем
график,
соответствующий
рис.
13.4.1,
для
случая,
когда
предел
из
п.
(Ь)
больше
1 +
(1
+8)(0://3)'"'(,
(е)
нарисуем
график,
соответствующий
рис.
13.4.1,
для
случая,
когда
предел
из
п.
(Ь)
не
превосходит
1 +
(1
+8)(0://3)'"'(.
Решение.
(а)
Mx{t)
=
е
а
[l-у'l-2t/,ВJ
ДЛЯ
t < /3/2;
таким
образом,
'"'(
=
/З/2.
(Ь)
lim
Mx(t)
=
еО'.
t----t,В/2
(с)
1 +
(1
+
В)(о://3)т
=
е
а
[l-V
l
-
2t
/,ВJ
для
t < /3/2.
13.4.
Вероятности
разорения и
распределение
страховых
выплат
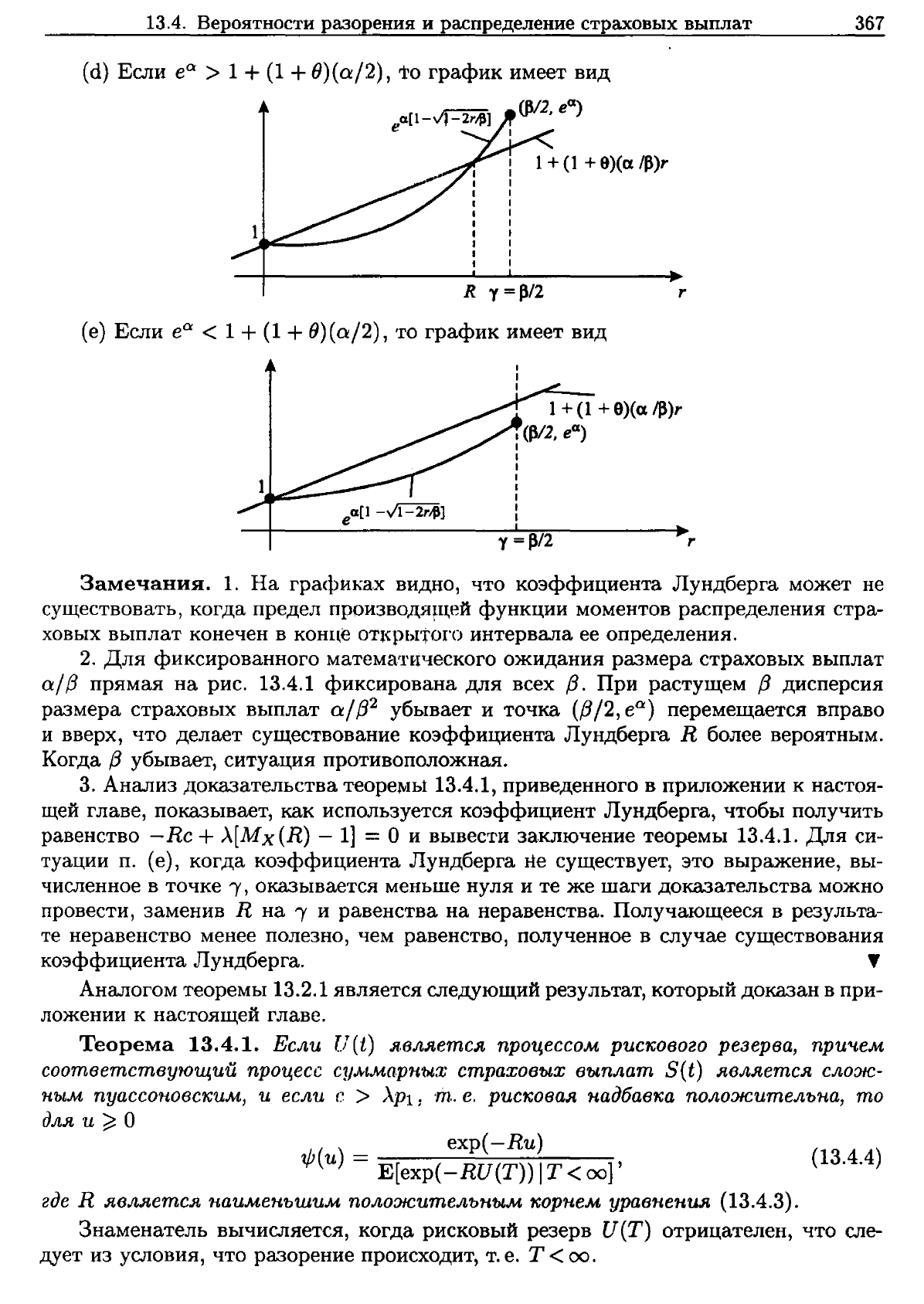
(d)
Если
е
а
> 1+
(1
+
О)(а/2)
,
то
график
имеет
вид
(lV2,
га)
1+
(1
+
8)(а
jp)r
367
R
'у
==
Р/2
(е)
Если
е
а
< 1 +
(1
+
О)(а/2)
,
'Го
график
имеет
вид
r
1+
(1
+
8)(а
jp)r
IOV2,
еа)
I
I
I
I
I
I
I
I
r
(13.4.4)
Замечания.
1.
На
графиках
видно,
что
коэффициента
Лундберга
может
не
существовать,
когда
предел
ПРОИЗВОдЯfцей
функции
моментов
распределения
стра
ховых
выплат
конечен
в
конце
открытого
интервала
ее
определения.
2.
Для
фиксированного
математического
ожидания
размера
страховых
выплат
0./
/3
прямая
на
рис.
13.4.1
фиксирована
для
всех
fЗ.
При
растущем
f3
дисперсия
размера
страховых
выплат
а/
fЗ2
убывает
и
точка
«(3/2,
е
СЖ
)
перемещается
вправо
и
вверх,
что
делает
существование
коэффициента
Лундберга
R
более
вероятным.
Когда
(3
убывает,
ситуация
противоположная.
3.
Анализ
доказательства
теоремь!
13.4.1,
приведенного
в
приложении
к
настоя
щей
главе,
показывает,
как
используется
коэффициент
Лундберга,
чтобы
получить
равенство
-Rc
+
л[м
х
(R) -
1]
=
О
и
вывести
заключение
теоремы
13.4.1.
Для
си
туации
п.
(е),
когда
коэффициента
Лундберга
не
существует,
это
выражение,
вы
численное
в
точке
"
оказывается
меньше
нуля
и
те
же
шаги
доказательства
можно
провести,
заменив
R
на
,
и
равенства
на
неравенства.
Получающееся
в
результа
те
неравенство
менее
полезно,
чем
равенство,
полученное
в
случае
существования
коэффициента
Лундберга.
~
Аналогом
теоремы
13.2.1
является
следующий
результат,
который
доказан
в
при
ложении
к
настоящей
главе.
Теорема
13.4.1.
Если
U(t)
,я,вляется
nроцессом
риС7Сового
резерва,
nри'Чем
соответствующий
процесс
Сll.м.м.ар'Н'Ых
страховых
выплат
S(t)
.являетс.я
слож
ным
nуассо'Новс'Х;и.м.,
и
если
с
>
'\Рl;
т
..
е.
рисковая
'Надбавка
nоложитель'На,
то
дл.я
и
~
О
'Ф
и
_
ехр(
-Ru)
( ) -
Е[ехр(
-RU(T))
I
Т
<00]'
где
R
.явл.яетс,Я
наи.м.еньшим
положительным
7Сорн.е.м.
урав'Не'Н'UЯ
(13.4.3).
Знаменатель
вычисляется,
когда
рисковый
резерв
И
(Т)
отрицателен,
что
сле
дует
из
условия,
что
разорение
происходит,
т.
е.
Т <
00.

368
Гл.
13.
Модели
коллективных
рисков
на
длительном
интервале
времени
Из
рис.
13.4.1
видно,
что
если
(}
--t
О,
1'р
секущая
приближается
к
касательной
к
графику
функции
Mx(t)
в
f'очке
r =
О,
откуда
вытекает,
что
R --t
О.
Тогда,
согласно
формуле
(13.4.4),
Ifмеем
феи)
= 1,
Т.е.
разорение
непременно
произойдет.
Далее,
И(t),
t >
О,
дЛЯ
случая
В
<
О
всегда
меньше,
чем
И(t)
для
В
--t
О,
и
поскольку
разорение
непременно
произdйдет
прН
f)
==
О,
оно
обязательно
произойдет
при
f)
<
О.
I
Из
этих
соображений
мы
предполщ'асм,
что
В
>
О.
В
общем
случае
вычислить
выражение,
которое
стоит
в
знаменателе
формулы
(13.4.4),
в
замкнутой
форме
невозможно.
Исключение
составляет
случай
и
=
О
(см.
упр.
13.10)
и
случай,
когда
страховые
выплаты
имеют
показательное
распределение
(см.
пример
13.4.4).
Однако
эту
теорему
можно
использовать
для
выведения
нера
венств.
Поскольку
С.в.
И
(Т)
при
условии,
что
Т
<
00,
непременно
отрицательна,
знаменатель
в
(13.4.4)
больше
1.
Отсюда
следует,
что
(13.4.5)
Если
распределение
величины
страховых
выплат
ограничено
таким
образом,
что
Р(m)
= 1
для
некоторого
конечного
т,
то
при
условии,
что
Т
<
00,
имеем
И(t)
>
-т,
поскольку
величина
рискового
резерва
непосредственно
перед
страховыми
вы
платами,
приведшими
к разорению,
должна
быть
положительной.
Таким
образом,
(13.4.6)
Некоторые
авторы
предлагаfЬТ
использовать
приближение
1/{L~)
".1
e-
Ru
,
(13.4.7)
которое
в
силу
неравенства
(13.4.5)
завышает
вероятность
разорения.
Перейдем
теперь
к
анализу
частного
случая,
когда
для
получения
явного
выра
жения
для
вероятности
разорения
ф(и)
может
использоваться
теорема
13.4.1.
Пример
13.4.4.
Вычислим
вероятность
разорения,
когда
величина
страховых
выплат
имеет
показательное
распределение
с
параметром
(3
>
О.
Решение.
Пусть
разорение,
если
оно
происходит,
случается
в
момент
Т.
Пусть
й
является
величиной
рискового
резерва
непосредственно
перед
моментом
Т.
Событие
-И(Т)
>
у
можно
переформулировать
как
такое
событие,
что
Х,
величина
выплаты
по
страховому
случаю,
повлекшему
разорение,
больше
и
+
у
при
условии,
что
она
больше
u.
Условная
вероятность
этого
события
задается
выражением
а
Г
ОО
-[Зх
d
1-'
Ju+li
е
х
_
-/ЗУ
00
-
е
,
(3
fu
е-/ЗЖ
dx
так
что
функция
плотности
с.в.
-и(т)
при
условии
Т
<
00
равна
d
dy
(1
-
е-'ВУ)
=
(3е-/ЗУ.
Таким
образом,
Е[ехр(
-RИ(Т))
I
Т
<
00]
=
/3
{ОО
e-/ЗУе
Rу
dy
=
{3
.
J
o
{3
- R
Нам
известно
из
при
мера
13.4.1,
что
коэффициент
Лундберга
в
этом
случае
имеет
вид
R =
()/3/(1+В).
Комбинируя
это
равенство
с
(13.4.4),
мы
приходи
м
к
следующему

13.5.
Величина
рискового
резерва,
впервые
оказавшегося
ниже
начального значения
3б9
выражению:
_
((3
-
R)e-
Ru
__
.1
_
(-в(3и)
Ф
(
и)
-
!з
- 1 +
()
ехр
1 +8
1
[-вu]
1 +8
ехр
(1
+
8)Рl
.
(13.4.8)
13.5.
Величина
рискового
резерва,
впервые
оказавшегося
ниже
начального
значения
(13.5.2)
(13.5.1)
поскольку
1
{ОО
1
(1
+
B)Pl
Jo
[1
-
Р(у))
dy = 1 +
8'
100
[1
-
р(у)]
dy =
Рl'
В
частном
случае
и
=
О
равенство
(13.5.1)
определяет
вероятность
того,
что
ве
личина
рискового
резерва когда-либо
окажется
меньше
нуля,
т.
е.
его
начального
значения.
Поэтому
1
ф(О)
= 1+
В
Примечательно,
что
ф(О)
зависит
только
от
относительной
рисковой
надбавки
В
и
не
зависит
от
структуры
распределения
величин
страховых
выплат.
Заметим,
что
функция
Продолжим
рассмотрение
модели
с
непрерывным
временем,
в
которой
процесс
S(t)
суммарных
страховых
выплат
является
сложным
пуассоновским.
В
настоящем
разделе
мы
будем
рассматривать
величину
рискового
резерва
в
тот
момент,
когда
он
впервые
оказался
ниже
своего
начального
значения
(конечно,
этого
может
никогда
не
случиться).
В
качестве
приложения
мы
найдем
простое
выражение
для
11'(0),
вероятности
разорения
в
случае,
когда
начальное
значение
рискового
резерва
равно
нулю.
Основная
теорема
этого
раздела,
доказательство
которой
содержится
в
прило
жении
к
настоящей
главе,
формулируется
следующим
образом.
Теорема
13.5.1.
Для
сло:»сного
nуассоновс'Х;ого
nроцесса
вероятность
того,
'Что
велu'Чuна
PUC'lCOBOlO
резерва
'Х;огда-лuбо
О'ICа:»сется
.меньше
своего
на'ЧалыtOго
зна'Ченuя
и,
впервые
О'ICазавшuсь
ме:»сду
велu'Чuнамu
и
-
у
и
и
-
у
-
dy,
равна
л
.
1-Р(у)
~
[1
-
Р(у)]
dy =
(1
+
8)Pl
dy,
У
>
О.
в
качестве
приложения
теоремы
13.5.1
заметим,
что
вероятность
того,
что
ве
личина
рискового
резерва
когда-либо
окажется
меньше
его
начальной
величины,
равна
л
(1
_
Р(у)]
= 1-
Р(у)
,
с
.
(1
+В)Рl
у>
О,
не
является
функцией
ПЛОТ1iЬС1'И,
поскольку
интеграл
от
нее не
равен
единице.
Од
нако
с
ней
можно
связать
функцию
плотности.
Пусть
С.в.
L
1
-
величина,
на
кото
рую
рисковый
резерв
оказывается
MeHbIile
начального
значения
в
первый
раз,
если
это
действительно
происходит.
Функция
плотности
С.в.
L
1
получается
делением
на
ф(О)
=
1/(1
+
В)
величины
1 -
Р(у)
(1
+
8)Pl

370
Гл.
13.
Модели
коллективных
рисков
на
длительном
интервале
времени
и
имеет
вид
1
fL
1
(у)
=
-[1
-
Р(у)],
Рl
у>
О.
(13.5.3)
Связь
между
производящими
функциями
моментов
С.в.
L
1
и
случайной
величины
страховых
выплат
Х
устанаn,ш-lвается
с
помощью
интегрирования
по
частям:
ML
1
(1')
=
-.!.
(ОО
е
ТУ
[1
_
Р(у)]
dy =
~!_{
е
ТУ
[1
_
Р(у)]
00
+!
(ОО
еТУр(у)
d
Y
}
Рl
}
О
Рl
l'
О
r }
о
1
=
-[Mx(1')
-
1].
(13.5.4)
Рl
Т'
Мы
проиллюстрируем дальнейшие
приложения
теоремы
13.5.1
следующими
при
мерами.
Пример
13.5.1.
Выпишем
выражение
для
распределения
величины
рискового
резерва
в
первый
момент,
когда
он
упадет
ниже
исходного
значения
и,
при
усло
вии,
что
это
непременно
произойдет,
если
величина
выплаты
по
любому
страховому
случаю
равна
2.
Решение.
Мы
имеем
l_р(у)={1,
О,
о
~
у
< 2,
у
~
2.
Поэтому
функция
плотности
С.В.
L
1
имеет
вид
-'!'[1-
Р(у)]
= {1/2'
Рl
О
о
~
у
< 2,
в
противном
случае.
Таким
образом,
С.в.
L
1
равномерно
распределена на интервале
от
О
до
2
и
величина
рискового
резерва
после
первого
падения
ниже
уровня и
равномерно
распределена
на
интервале
от
и
- 2
до
U.
,
Пример
13.5.2.
Выпишем
выражение
для
распределения
с.в.
L
1
,
если
величина
индивидуальной
выплаты
имеет
показательное
распределение
с
параметром
[3.
Решение.
Поскольку
1 -
Р(у)
=
е-{3У
для
у
>
О,
функция
плотности
С.в.
Ll
имеет
вид
1
-[1
-
Р(у)]
=
[3е-
13У
,
Рl
у>
О.
Таким
образом,
распределение
С.в.
L
1
также
является
показательным
с
парамет
ром
/З.
"
13.6.
Максимальные
суммарные
потери
Новая
случайная
величина,
называемая
.мmссu.м.ал'Ьн'Ы.м;и
су.м;.м;арн'Ым.и
потеря
ми,
определяется
соотношенцем
L =
Пlах{S(t)
- ct}
t~O
(13.6.1)
и
является
максимальным
превышением
суммарных
выплат
над
собранными
пре
миями.
Так
как
S(t) -
ct
=
О
для
t =
О,
то
L
~
О.
