Бауэрс Н., Гербер Х., Джанс Д., Несбитт С., Хикман Дж. Актуарная математика
Подождите немного. Документ загружается.

12.4.
Свойства
некоторых
сложных
распределений
341
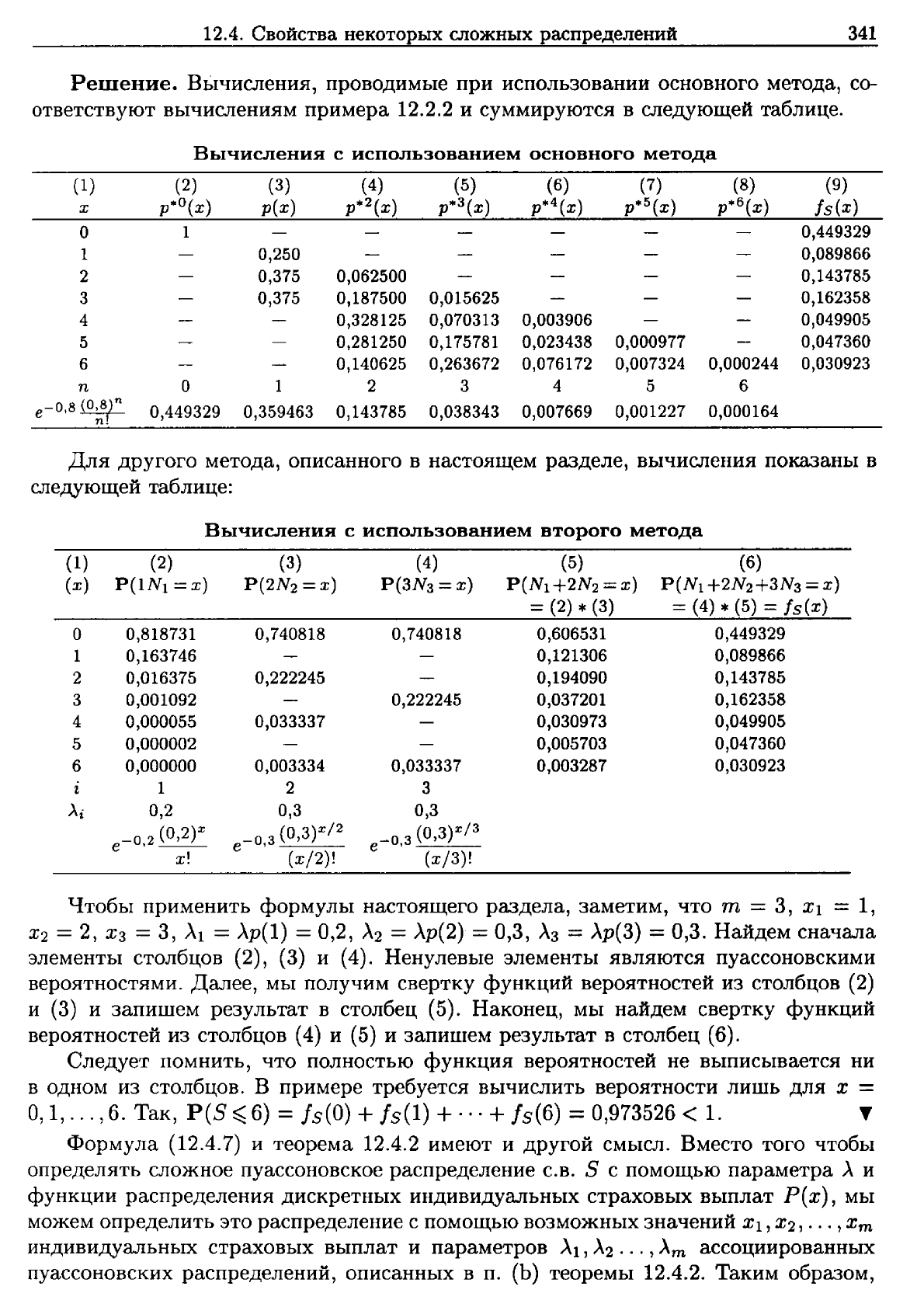
Решение.
выIисления,'
проводимые
при
использовании
основного
метода,
со-
ответствуют
вычислениям
примера
12.2.2
и
суммируются
в
следующей
таблице.
Вычисления
с
использованием
основного
метода
(1) (2) (3) (4) (5) (6)
(7) (8)
(9)
х
р"О(х)
р(х)
р
..
2(х)
р"З(х)
р
..
4(х)
р
..
5(х)
р
..
6(х)
fs(x)
О
1
0,449329
1
0,250
0,089866
2
0,375
0,062500
0,143785
3
0,375 0,187500 0,015625
0,162358
4 0,328125 0,070313 0,003906
0,049905
5
0,281250
0,175781
0,023438 0,000977 0,047360
6 0,140625
0,263672 0,076172 0,007324 0,000244 0,030923
n
О
1 2 3 4 5 6
e-O.8~
0,449329 0,359463 0,143785 0,038343 0,007669
0,001227
0,000164
n!
Для
другого
метода,
описанного
в
настоящем
разделе,
вычисления
показаны
в
следующей
таблице:
Вычисления
с
использованием
второго
метода
(1) (2) (3) (4) (5) (6)
(х)
P(INl
=
х)
P(2N2
=х)
Р(3Nз
=х)
P(Nl
+2N2
=
х)
P(Nl
+2N2+3Nз
=
х)
= (2) *(3)
= (4) *(5) =
fs(x)
о
0,818731 0,740818 0,740818 0,606531
0,449329
1 0,163746
0,121306 0,089866
2 0,016375 0,222245 0,194090
0,143785
3 0,001092 0,222245 0,037201
0,162358
4
0,000055
0,033337 0,030973 0,049905
5
0,000002 0,005703 0,047360
6 0,000000
0,003334 0,033337 0,003287 0,030923
z
1 2
3
Лi
0,2 0,3 0,3
-о
2
(О,2)Х
(О
з)х/2
(О
З)Х/З
е
'
е-О,З
'
е-О,З
'
х!
(х/2)! (х/3)!
Чтобы
применить
формулы
настоящего
раздела,
заметим,
что
т
= 3,
Хl
= 1,
Х2
=2,
хз
=
3,}.1
=
}.р(l)
=0,2,}.2 =
}.р(2)
=
0,3,}.з
=
}.р(3)
= 0,3.
Найдем
сначала
элементы
столбцов
(2),
(3)
и
(4).
Ненулевые
элементы
являются
пуассоновскими
вероятностями.
Далее,
мы
получим
свертку
функций
вероятностей
из
столбцов
(2)
и
(3)
и
запишем
результат
в
столбец
(5).
Наконец,
мы
найдем
свертку
функций
вероятностей
из
столбцов
(4)
и
(5)
и
запишем
результат
в
столбец
(6).
Следует
помнить,
что
полностью
функция
вероятностей
не
выписывается
ни
в
одном
из
столбцов.
В
примере
требуется
вычислить
вероятности
лишь
для
х
=
0,1,
...
,6.
Так,
Р(В
~
6)
=15(0) +15(1) +... +
15(6)
=0,973526 < 1.
~
Формула
(12.4.7)
и
теорема
12.4.2
имеют
и
другой
смысл.
Вместо
того
чтобы
определять
сложное
пуассоновское
распределение
с.в.
S
с
помощью
параметра
}.
и
функции
распределения
дискретных
индивидуальных
страховых
выплат
Р(х),
мы
можем
определить
это
распределение
с
помощью
возможных
значений
Хl,
Х2,
•••
,
Х
т
индивидуальных
страховых
выплат
и
параметров
}.1,}.2
...
,}.т
ассоциированных
пуассоновских
распределений,
описанных
в
п.
(Ь)
теоремы
12.4.2.
Таким
образом,

342
Гл.
12.
Модели
коллективных
рисков
на
коротком
интервале
времени
для
Xi
имеется
ассоциированное
пуассоновское
распределение
С.в.
Ni
с
парамет
ром
Лi.
Используя
это
новое
распределение
с.в.
S,
из
равенств
E[N
i
]
=
D[N
i
]
=
Лi
и
независимости
с.в.
N
i
мы
получаем
E[S] =
Е
[~XiNi]
=
~X;),i,
D[S] =D
[~X;Ni]
=
~
X~
),i.
(12.4.13)
(12.4.14)
Формула
(12.4.13)
может
быть
получена
из
равенства
(12.3.2),
если
заметить,
что
m m
ЛРl
=
Л
L
Х{7Т"i
=L
ХiЛi.
i=l
i=l
Аналогично
мы
можем
получить
формулу
(12.4.14)
из
(12.3.3).
В
некоторых
случаях
полезно,
как
в
примере
12.4.1,
рассматривать
С.в.
S
как
сумму
взаимно
независимых
случайных
величин
XiNi,
i =1,
2,
...
,
т,
где
с.в.
XiNi
имеет
сложное
пуассоновское
распределение
с
параметром
Лi
и
вырожденным
рас
пределением
величины
страховых
выплат,
сосредоточенным
в
точке
Xi.
Эта
интер
претация вытекает
из
теоремы
12.4.2
и
лежит
в
основе
второго
метода
вычислений,
который
иллюстрируется
в
примере
12.4.2.
Если
величины
страховых
выплат
могут
быть
только
положительными
целыми
числами,
имеется
третий
метод
вычисления
некоторых
сложных
распределений,
на
зываемый
рекуррентн'ы.м
.м.етодо.м.
Он
основан
на
рекуррентной
формуле,
которая
выводится
в
следующей
теореме.
Теорема
12.4.3.
Пусть
распределение
вероятностей
С.в.
N,
'Числа
cmpaXOB'bLX
слу'Чаев,
удовлетворяет
условию
P(N=n)/P(N=n
-1)
=
а+(Ь/n)
для
n =
1,2,
...
,
а
распределение
вели'Чин
страховых
выплат
сосредото'Чено
на
МНОЭICестве
положи
тельных
целых
'Чисел.
Тогда
для
слоЭICН'ЫХ
распределений
С.в.
S
х
[
Ьi]
fs(x)
=
~
а
+;-
p(i)fs(x
- i),
Х
= 1,2,
...
,
nри'Чем
на'Чальное
зна'Ченuе
определяется
равенством
18(0) =
P(N
=
О)
.
Для
доказательства
этой
теоремы
нам
потребуется
следующая
лемма.
Лемма.
Для
незавuсимых
U
одинаково
распределенных
с.
в,
Х
1,
Х
2,
Х
3,
...
,
Х
n,
nрuнимающuх
зна'Ченuя
в
.множестве
nОЛОЭICuтельных
целых
'Чuсел,
U
для
поло
жительного
целого
'Числа
Х
х
(i)
р.n(х)
=
LP(i)p*(n-l)(х
- i),
i=l
х
(ii)
р*n(х)
= n L ip(i)p*(n-l)(x - i).
х
i=l
Доказательство
леммы.
Для
n = 1
обе
формулы,
(i)
и
(ii),
сводятся
к
ра
венству
p.l(x)
=
р(х)р·О(о).
Для
n > 1
проверку
формулы
(i)
можно
провести,

12.4.
Свойства
некоторых
сложных
распределений
343
используя
формулу
полной
вероятности,
которая
позволяет
представить
Р(Х
1
+
Х
2
+
...
+
Х
n =
х)
в
виде
х
L
Р(Х
1
= i)
Р(Х
2
+
Х
з
+
...
+
Х
N
=
Х
- i).
i=l
Далее,
заметим,
что
Р(Х
2
+
Х
з
+ ... +
Х
N
=
Х
- i)
и
Р(Х
1
+
Х
2
+
...
+
Х
N
=
х)
можно
вычислить,
используя
(n -
l)-кратную
и
n-кратную
свертки
функции
p(i)
соответственно
(см.
формулу
(2.3.4)).
Для
n > 1
мы
получим
формулу
(ii),
рассматривая
условные
математические
ожидания
E[X
k
I
Х
1
+
Х
2
+
Х
з
+
...
+
Х
N
=
х]
для
k =
1,2,3,
...
,
n.
Из
сооб
ражений
симметрии
эти
величины
одинаковы
для
всех
k.
Поскольку
их
сумма
равна
х,
каждое
слагаемое
равно
х/n.
Для
условного
математического
ожидания
E(X
k
I
Х
1
+
Х
2
+
Х
з
+
...
+
Х
N
=
х]
получается
формула
х
L
iP(X
1
= i)
Р(Х
2
+
Х
з
+
...
+
Х
N
=
Х
-
i)/P(X
1
+
Х2
+
Х
З
+
...
+
Х
N
=
х).
i=l
Заметим,
что
Р(Х
2
+
Х
З
+
...
+
Х
N
=
Х
- i)
и
Р(Х
1
+
Х
2
+
Х
З
+
...
+
Х
N
=
х)
можно
вычислить,
используя
(n -
l)-кратную
и
n-кратную
свертки
функции
p(i).
Выражая
отсюда
р"'n(х)
,
мы
завершает
доказательство
леммы.
•
Доказательство
теоремы.
Прежде
всего,
00
fs(x)
=
LP(N=n)p"'n(x).
n=l
Учитывая,
что
P(N
=n) =
(а
+
(Ь/n))
P(N
=n - 1),
мы
получаем
00 00
ь
fs(x)
=
а
L
P(N=n
-1)р·n(х)
+ L -
P(N=n
-1)р·n(х)
n
n=l
n=1
и,
воспользовавшись
обеими
частями
леммы,
00
ж
fs(x)
=
а
L
P(N
= n -
1)
LP(i)p",(n-l)
(х
- i)
n=l
i=l
00
ж
+ L
~
P(N=n-1):
Lip(i)p*(n-l)(x
- i).
n=l
i=l
Меняя
порядок
суммирования,
получаем
х
00
fs(x)
=
а
LP(i)
L
P(N
= n
-1)
p.(n-l}(x
- i)
i=1
n=1
Ь х
00
+ - L ip(i) L
P(N
=n
-1)
p.(n-l)(x
- i)
Х.
2=1
n=1
=
а
tP(i)fs(x
- i) + : t
ip(i)fs(x
-
i)
= t
(а
+
~)P(i)fs(x
- i). •

344
Гл.
12.
Модели
коллективных
рисков
на
коротком
интервале
времени
Рассмотрим
те
единственные
три
распределения,
которые
удовлетворяют
соот
ношению
между
последовательными
значениями
вероятности
P(N
=
n),
сформули
рованному
в
условии
теоремы
12.4.3.
(а)
Пуассоновское
распределение:
P(N
=
n)/P(N
=n
-1)
=
Л/n.
Рекуррентная
формула
для
сложного
пуассоновского
распределения
имеет
вид
fs(x)
=
л
t
ip(i)fs(x
- i)
при
Is(O) =
е-Л.
х.
t=l
(12.4.16)
(Ь)
Отрицательное
биномиальное
распределение:
P(N=n)/P(N=n-1)
(1
-
р)(n
+
т
-
1)/n,
так
что
а
= 1 -
р
и
Ь
=
(1
-
Р)(Т
- 1).
Рекуррентная
фор
мула
для
сложного
отрицательного
биномиального
распределения
имеет
вид
Is(x)
=
(1
-
р)
t
[(Т
-
1)~
+1
]P(i)ls(x
- i)
при
Is(O) =
р
Т
•
(12.4.17)
(с)
Биномиальное
распределение
с
параметрами
т
и
р:
P(N=n)
т+1-n
Р
P(N=n-1)
n
1-р'
так
что
а
=
-р/(l-
р)
и
Ь
=
(т
+
l)р/(l-
р).
Рекуррентная
формула
в
этом
случае
имеет
вид
(12.4.18)
х
=
1'2'
....
Пример
12.4.2
(повторное
вычисление).
Для
сложного
пуассоновского
распре
деления
из
этого
примера
вычислим
fs(x)
=
P(S=
х)
рекуррентным
методом.
Решение.
Подставляя
значения,
использовавшиеся
при
втором
методе
вычис
лений,
в
формулу
(12.4.16),
получим
1
Is(x)
=
-[0,2fs{x
- 1) +
0,6fs(x
-
2)
+
0,9fs(x
- 3)],
х
Вспоминая,
что
f8{X) =
О,
Х
<
О,
и
что
18(0) =
е-Л
=0,449329,
мы
легко
получим
снова
значения
функции
1s
(х),
найденные
ранее
с
применением
основного
метода
вычислений.
~
12.5.
Аппроксимации
распределения
суммарных
выплат
В
разд.
2.4
для
аппроксимации
распределения
суммарных
страховых
выплат
в
модели
индивидуальных
рисков
использовалось
нормальное
распределение.
Оно
будет
первым
из
распределений,
которые
мы
рассмотрим
здесь
применительно
к
модели
коллективных
рисков.
~ля
сложного
пуассоновского
распределения
два
параметра
нормальной
ап
проксимации
определяются
соотношениями
(12.3.2)
и
(12.3.3).
~ля
сложного
от
рицательного
биномиального
распределения
параметры
определяются
формулами
(12.3.10)
и
(12.3.11).
В
каждом
ИЗ
этих
двух
случаев
аппроксимация
лучше,
если
больше
математическое
ожидание
числа
страховых
случаев,
или,
другими
словами,
когда
в
случае
сложного
пуассоновского
распределения
л
велико
и
когда
в
случае

12.5.
Аппроксимации
распределения
суммарных
выплат
345
(12.5.1)
отрицательного
биномиального
распределения
r
велико.
Эти
два
результата
содер
жатся
в
теореме
12.5.1,
которую
можно
интерпретировать
как
вариант
центральной
предельной
теоремы.
Теорема
12.5.1.
(а)
Если
С.В.
S
'U.Мeeт
сложное
nуассо'Н,овское
расnределе'Н,ие
с
nара,м,етро,м,
л
и
с
функцией
расnределенuя
вели-ч.ины
и'Н,дивидуаль'Н,ых
страхов'Ых
в'ыnлат
Р(х),
то
распределение
С.В.
z = S -
ЛР1
';ЛР2
сходитс,я
при
л
~
00
к
ста'Н,дарт'Н,ому
'Н,ормаль'Н,ому
расnределе'Н,ию.
(Ь)
Если
с.
в.
S
имеет
сложное
отрицатель'Н,ое
биномиаль'Н,ое
расnределе'Н,ие
с
nара,м,етра,м,и
т,
р
и
с
фУ'Н,'IC'Цией
расnределе'Н,и,я
вели'Чин'Ы
и'Н,дивидуаль'Н,ых
страхо
В'ЫХ
выплат
Р(х),
то
распределение
С.В.
z = S - r(q/p)P1
vr(Q/p)P2
+
r(q2
/р
2
)р!
сходитс,я
при
r
~
00
к
стандартно,м,у
нормальному
распределению.
Доказательство.
Мы
докажем
утверждение
(а),
показав,
что
Нт
Mz(t)
=
ее
/2.
),-+00
(12.5.2)
(12.5.3)
(12.5.5)
(12.5.4)
Утверждение
(Ь)
можно
доказать
аналогичным
образом,
но
потребуются
некоторые
дополнительные
шаги.
Из
формулы
(12.5.1)
вытекает,
что
Mz(t) =
Ms(~)
ехр
( -
~).
Воспользуемся
формулой
(12.3.5)
и
получим
Mz(t) =
ехр
{>'[Мх
(vk)
-1]
-
~},
а
затем
подставим
разложение
Р1
t
P2
t2
Mx(t)
=
1+
- + - +
...
1!
2!
'
где
t
заменяется на
t/';ЛР2,
в
(12.5.3).
Тогда
(
1
2 1 1
рз
3 )
Mz(t)=exp
-t
+---t
+
...
2 6
Д
3/2
.
Р2
Таким
образом,
если
л
~
00,
то
Mz(t)
приближается
к
e
t2
/
2
,
а
это
производящая
функция
моментов
стандартного
нормального
распределения.
•
Нормальное
распределение
может
не
быть
наилучшим
приближением
ДЛЯ
рас
пределения
суммарных
страховых
выплат,
поскольку
оно
симметрично,
а распре
деление
суммарных
страховых
выплат
часто
асимметрично.
Эта
асимметричность
отчетливо
видна
в
табл.
12.5.1,
которая
показывает,
что
третий
центральный
момент
С.в.
S
при
каждом
ИЗ
двух
рассматривавшихся
распределений,
сложном
пуассонов
ском
или
сложном
отрицательном биномиальном,
не
равен
О.
ДЛЯ
распределений

346
Гл.
12.
Модели
коллективных
рисков
на
коротком
интервале
времени
страховых
случаев
положительной
величины
Р(О)
=
О,
и
третий
центральный
мо
мент
С.в.
S
в
каждом
ИЗ
этих
случаев
положителен.
Таблица
12.5.1.
Вычисление
третьего
центрального
момента
С.В.
S
Распределение
S
Шаг
Сложное
пуассоновское
Ms(t)
ехр{л[Мх(t)
- 1]}
ln
Ms(t)
л{Мх(t)
-
1]
d
3
dt
3
ln
Ms
(t)
лмх
(t)/11
Е[(В
-
Е[В])3]
лрз
=
dd
З
з
ln Ms(t)I
1)
t
t=O
Сложное
отрицательное
биномиальное
[l-q~Х(tJ
r
lnp
- r
ln(l
-
qMx(t)]
rqM'J/(t)
+
з
rq
2
M~(t)M~(t)
1 -
qMx
(t)
[1
-
qMx
(t)]2
+
2
rq
З(М'х
(t»З
[1
-
qMx
(t)]3
rqрз
3rq2plp2
2rqЗр~
--
+ +
----"'-~
р
р2
р3
При
составлении
табл.
12.5.1
мы
пользовались
свойствами
логарифма
произво
дящей
функции
моментов,
например,
d
A1~(0)
-d
ln A1x(t) =
А1
( ) =
1",
t
t=O
Х
О
~
1
М
()
-
M~(O)Mx(O)
-
M~(0)2
=
0'2.
dt2
n
х
t
t=o
Мх
(0)2
В
упр.
12.23(а)
читателю
предлагается
проверить
соотношение,
использованное
в
последней
строке
табл.
12.5.1.
Из-за
отмеченной
выше
асиммертичности
нам
нужно
найти
более
общую
ап
проксимацию
для
распределения
суммарных
выплат,
которая
учитывает
эту
асим
метричность.
Поиски
этой
второй
аппроксимации
мы
начнем
с
гамма-распределения.
Этот
выбор
мотивируется
тем,
что как
гамма-распределение,
так
и
сложное
пуас
соновское
и
сложное
отрицательное
биномиальное
распределения
для
положитель
ных
страховых
выплат
имеют
положительный
третий
центральный
момент.
Пусть
G(x:
(У,
(3)
обозначает
функцию
распределения
с
параметрами
Q
и
(3,
т.
е.
а(х:
0.,
fЗ)
=
1
Ж
~:)
t"'-l
е-/Зt
dt. (12.5.6)
В
этом
случае
для
любого
Ха
определим
новую
функцию
распределения,
которая
будет
обозначаться
через
Н
(х
:
(У, {З,
хо),
следующим
образом:
Н(х:
(У,
(3,
хо)
=
О(х
-
Ха
:
(У,
(3).
(12.5.7)
Это
равносильно
сдвигу
распределения
О(х:
(У,
fЗ)
на
величину
хо.
Рис.
12.5.1
ил
люстрирует
этот
сдвиг
ДЛЯ
хо
>
О,
когда
и(х),
х
~
Ха,
и
h(x),
х
~
Хо,
обозначают
плотности
распределений
О(х:
(У,
(3)
И
Н(х:
(У,
/3,
хо)
соответственно.
d
k
I
I)Если
k
~
4,
то
-k
(п
Ms(t)
не
является
k-M
центральным
моментом.
dt
t=O

12.5.
Аппроксимации
распределения
суммарных
выплат
Рис.
12.5.1.
Гамма-распределение
со
сдвигом
347
Мы
аппроксимируем
распределение
суммарных
выплат
с.в.
S
гамма-распре
делением
со
сдвигом,
в
котором
параметры
а,
(3
И
Ха
выбраны
таким
образом,
чтобы
первtIЙ
момент, а
также
второй
и
третий
центральные
моменты
С.в.
S
совпадали
с
соответствующими
характеристиками
гамма-распределения
со
сдвигом.
Поскольку
центральные
моменты
такого
гамма-распределения
совпадают
с
центральными
мо
ментами
исходного
гамма-распределения,
эта
процедура
приводит
к
соотношениям
ct
E[S)
=
Ха
+ /3'
ct
D[S]
=
(32'
Е[(В
-
E[SJ)3]
=
~~
.
Из
этих
соотношений
мы
имеем
D[S)
/3
= 2 E[(S _ E[S))3J'
[D[S]]3
ct
= 4 E[(S _
Е[S])З)2'
[D[S]]2
Ха
=
E[S)
- 2E[(S _
E[S))3)
.
(12.5.8)
(12.5.9)
(12.5.10)
(12.5.11)
(12.5.12)
(12.5.13)
Для
сложного
пуассоновского
распределения
эта
процедура
при
водит
к
формулам
P~
ct =
4А
2'
(12.5.14)
Рз
/3
= 2
Р2
, (12.5.15)
Рз
р2
Ха
=
АР1
-
2А
2.
(12.5.16)
Рз
Замечание.
Мы
можем
показать,
что
если
а
---+
00,
/3
---+
00
и
Ха
-t
-00,
так
что
ct
Ха
+
(3
=
J.L
(постоянная),
~
= (12
(постоянная),
/32
(12.5.17)

348
Гл.
12.
Модели
коллективных
рисков
на
коротком
интервале
времени
то
распределение
Н(х:
сх,
(3,
хо)
сходится
к
N(p,
(72).
Таким
образом,
нормальные
распределения
содержатся
в
качестве
предельных
распределений
в
семействе
трех
параметрических
гамма-распределений.
В
этом
смысле
такая
аппроксимация
явля
ется
обобщением
нормальной.
Пример
12.5.1.
Рассмотрим
пуассоновское
распределение
с
параметром
л
=
16.
Это
то
же
самое,
что
сложное
пуассоновское
распределение
с
л
= 16
и
вырож
денным
распределением
величины
страховых
выплат,
сосредоточенным
в
точке
1.
Сравним
это
распределение
с
его
аппроксимациями
(а)
гамма-распределением
со
сдвигом,
(Ь)
нормальным
распределением.
Решение.
(а)
Здесь
Pk
= 1, k =
1,2,3,
и
из
формул
(12.5.14)-(12.5.16)
мы
имеем
а
=64,
f3
=2,
ХО
=
-16.
Заметим,
что,
в
отличие
от
случая,
изображенного
на
рис.
12.5.1,
Ха
отрицательно.
(Ь)
ДЛЯ
нормальной
аппроксимации
воспользуемся
значениями
р
= 16
и
(7 =
4.
Приведенные
в
таблице
ниже
результаты
позволяют
сравнить
эти
три
распре
деления.
В
этих
приближениях
при
аппроксимации
функции
распределения
Fs(x)
для
х
=5,10,
...
,40
использовалась
половинная
коррекция.
Точное
Аппроксимации
х
е-
16
(16)У
С(х
+16,5: 64, 2)
Ф(х
+0,5 -
16/4)
х
L:
,
у=о
у.
5
0,001384 0,001636
0,004332
10
0,077396 0,077739
0,084566
15
0,466745 0,466560
0,450262
20
0,868168
0,868093
0,869705
25
0,986881 0,986604
0,991226
30
0,999433 0,999378
0,999856
35
0,999988
0,999985
0,999999
40
1,000000 1,000000
1,000000
...
в
случае
сложного
отрицательного
биномиального
распределения
имеется
до
полнительное
соображение
в
пользу
приближения
гамма-распределением.
Оно
из
ложено
в
приложении
к
настоящей
главе.
12.6.
Замечания
и
литература
Глава
2
книги
[SealI969]
содержит
обширный
обзор
литературы
о
моделях
кол
лективных
рисков,
включая
работы
Лундберга
о
сложных
пуассоновских
распре
делениях.
Ряд
авторов,
например,
Дропкин
[Dropkin 1959]
и
Саймон
[Simon
1960]
использовали
отрицательное
биномиальное
распределение
для
моделирования
чис
ла
автомобильных
аварий,
совершенных
группой
страхователей
на
фиксированном
временном
интервале.
В
примере
12.3.1
мы
получили
отрицательное
биномиальное
распределение,
предположив,
что
неизвестный
пуассоновский
параметр
имеет
гамма-распределение.
Эта
идея
возникла
не
позже,
чем
появились
работы
Гринвуда
и
Юла
{Greenwood,
Yule 1920]
о
предрасположенности
к
авариям.
Другой
метод
получения
такого
рас
пределения
в
терминах
модели
заражения
принадлежит
Пой
а
и
Эггенбергеру;
его
можно
найти
в
гл.
2
книги
Бюльмана
{Buhlmann 1970].
В
частном
случае
целого
r

Приложение
349
отрицательное
биномиальное
распределение
может
быть
получено
как
распределе
ние
числа
бернуллиевских
испытаний,
которые
оканчиваются
неуспехом
вплоть
до
r-ro
успешного.
Изложение
этих
вопросов
можно
найти
в
большинстве
учебников
по
теории
вероятностей,
но
это
не
имеет
отношения
к
материалу
настоящей
главы.
Теорема
12.4.2
известна
давно,
и
ее
можно
найти
разд.
2
гл.
2
книги
Феллера
[Feller 1968].
Второй
метод
вычисления
вероятностей
ДЛЯ
сложного
пуассоновского
распределения,
основанный
на
теореме
12.4.2,
был
предложен
Песоненом
(Pesonen
1967]
и
реализован
Халмстадом
[Halmstad 1976]
при
вычислении
премий
в
страхо
вании
на
базе
эксцедента
убыточности.
Теорема
12.4.2
допускает
обратную
теорему,
которая
не
была
сформулирована
в
разд.
12.4.
Реньи
(Renyi 1962]
показал,
что
если
с.в.
N
1
,
N
2
,
...
, Nm
взаимно
независимы,
то
С.в.
N
распределена
по
пуассоновско
му
закону.
Поэтому
второй
метод
вычислений
будет
работать
только
для
сложного
пуассоновского
распределения.
у
казанный
второй
метод
вычислений
может
также
применяться
для
построения
имитационной
модели
для
суммарных
страховых
выплат.
Вместо
определения
вели
чины
индивидуальных
страховых
выплат
проводится
имитационное
моделирование
с.в.
N
1
,
N
2
,
...
, N
m
и
непосредственно
из
формулы
(12.4.7)
получается
реализация
с.в.
S.
При
применении
основного
метода
математическое
ожидание
количества
слу
чайных
чисел,
необходимого
для
однократного
нахождения
С.В.
S,
равно
1+
А.
При
применении
второго
метода
для
нахождения
каждого
значения
с.в.
S
требуется
ров
но
т
случайных
чисел.
Имеется
ряд
более
сложных
методов
приближения
распределения
суммарных
выплат.
В
книге
(Beard, Pentikiiinen, Pesonen 1984]
описан
метод
асимптотических
разложений
и
аппроксимации
Эшера.
Бохман
и
Эшер
(ВоЬтan,
Esscher 1963, 1964]
сравнивали
ряд
методов
аппроксимации.
Сил
(Seal
1978а]
привел
пример
прибли
жения
гамма-распределением
со
сдвигом
и
продемонстрировал
его
превосходное
ка
чество.
Бауэрс
[Bowers 1966]
аппроксимировал
распределение
суммарных
страхо
вых
выплат суммой
ортогональных
функций,
первая
из
которых
является
гамма
распределением.
Приведенный
в
приложении
к
этому
разделу
результат
о
том,
что
гамма-распределение
можно
получить
как
предел
сложного
отрицательного
бино
миального
распределения,
принадлежит
Лундбергу
(Lundberg 1940].
Иногда
распределение
суммарных
выплат
можно
получить
посредством
чис
ленного
обращения
производящей
функции
моментов;
эта
тема
развивается
в
гл.
3
книги
Сила
(Seal
1978Ь].
В
монографии
(Panjer,
WШmоt
1992]
идеи,
изложенные
в
этой
главе,
разви
ваются
более
подробно.
Особое
внимание
уделяется
рекуррентным
вычислениям
и
дискретным
аппроксимациям.
Приложение
Теорема
12.А.l.
Если
случайные
величины
SIc,
k =
1,2,3,
...
,
имеют
сложные
от
рицательные
биномиальные
распределения
с
nара.метрами
r
и
p(k)
и
с
фунtcцией
рас
пределения
страховых
выплат
Р(х)
и
если
параметры
отрицательных
бино.миальных
распределений
удовлетворяют
условиям
q(k) =
kfJ.
p(k)
р
для
k =
1,2,3,
...
,
где
q =
1-р
-
'l{;OHCmaHma,
то
распределение
С.в.
Sk/E[SIc]
приближает
G(x:
r,
r)
при
k
---t
00.

350
Гл.
12.
Модели
коллективных
рисков
на
коротком
интервале
времени
Доказательство.
Воспользовавшись
формулой
(12.3.12),
мы
получаем,
что
произво-
дящая
функция
моментов
с.в.
Sk/E[Sk]
равна
[
p(k)
]Т
()
(/
[ ])
(12.А.l)
1-
q k
Мх
t
Е
Sk
Кроме
того,
(
t)
Рl
Р2
2
Мх
E[Sk] = 1+ E[Sk] t +
2E[Sk]2
t +
....
Если
выражение
(12.А.2)
подставить
в
(12.А.l),
мы
получим
{
p(k)
}Т
1 - q(k) - [q(k)Pl/E[Sk]]t - [q(k)p2/2E[Sk]2]t2 -
...
Теперь,
поскольку
(12.А.2)
(12.А.3)
E{Bk]
=r q(k)Pl =r kqpl ,
p(k)
р
мы
видим,
что
производящей
функцией
моментов
с.в.
Sk/E[Sk]
является
[
1
Р2
2 ] - r
[1
]-r
1 - - t - t
-...
= 1 - - t -
R(
k) ,
r 2r
2
pHq/p)k
т
где
остаточный
член
R(k)
таков,
что
liШk-+оо
R(k)
=
О.
Таким
образом,
.~~
Е[
ехр
(t
Ef;.J)]
=
с
r
J,
(12.А.4)
что
представляет
собой
производящую
функцию
моментов
распределения
G(x:
т,
т).
•
Из
формулы
(12.А.4)
следует,
что
производящая
функция
моментов
С.в.
Bk
прибли
жается
выражением
(
r )
т
{
т
}Т
{ p(k)/[q(k)Pl]
}Т
Т
- E[Sk]t - r - [rq(k)/p(k)]Plt - p(k)/[q(k)Pl] - 1 '
которое
является
производящей
функццей
моментов
распределения
G{x:
т,
(P(k)/q(k)PIJ).
Таким
образом,
когда
k
велико,
откуда
в
предположениях
теоремы
12.А.1
следует,
что
велико
математическое
ожидание
числа
страховых
выплат
Tq(k)/p(k) =
rk(q/p)
,
распреде
ление
суммарных
выплат
приближенно
равно
гамма-распределению.
Теорема
12.А.l
должна
стать
аргументом
в
пользу
применения
гамма-распределений
для
аппроксимации
распределения
суммарных
выплат.
Сравнение
основных
соображений
теоремы
12.5.1(Ь)
и
теоремы
12.А.l
позволяет
глубже
проникнуть
в
суть.
Доказательство
теоремы
12.5.1
(Ь)
следует
доказательству
центральной
предельной
теоремы.
Если
перепи
сать
формулу
(12.5.2)
в
виде
z _
В/Т
- (q/p)pl
- V(q/p)P2
+
(q2
/p2)p~/..;r'
то
соответствие
станет
ясным,
причем
r
играет
роль
n
из
центральной
предельной
теоремы.
В
теореме
12.А.1
параметр
r
отрицательного
биномиального
распределения
остается
фиксированным.
Математическое
ожидание
числа
страховых
выплат
изменяется
пропор
ционально
параметру
объема
k
вследствие
изменения
величин
q(k)
и
p(k) = 1 - q(k).
В
предположениях
теоремы
12.А.l
rqk k
2
q2
2 [ В]
Р
1
D[B
k
] =
Р
Р2
+
Т];2
Рll
D
E[;k]
=
rkqp~
Р2
+;:.
Если
параметр объема
k
стремится
к
бесконечности,
то
D
[Ef;.J]
~
;,
что
следует
из
теоремы
12.А.l.
Поэтому
гамма-приближение
может
рассматриваться
в
от
рицательном
биномиальном
случае,
когда
математическое
ожидание
страховых
случаев
