Бауэрс Н., Гербер Х., Джанс Д., Несбитт С., Хикман Дж. Актуарная математика

Подождите немного. Документ загружается.

13.6.

Максимальные

суммарные

потери

371

Теорема

13.5.1

используется

для

доказательства

другой

теоремы,

которая

дает

явное

выражение

для

производящей

функции

моментов

С.в.

ЧТО

можно

использо

вать

для

получения

информации

(и).

качестве

приложения

получается

выра

жение

для

ф(и)

случае,

когда

распределение

индивидуальной

страховой

выплаты

является

взвешенной

суммой

показательных

распределений.

Для

того

чтобы

получить

функцию

распределения

с.в.

заметим,

что

при

1 -

ф(и)

=P[U(t)

для

всех

Р[и

+ct - S(t)

для

всех

= P[S(t) - ct:::;

для

всех

t].

Но

правая

часть

эквивалентна

P(L:::;

и),

и,

значит,

1 -

ф(и)

=P(L:::;

и),

О.

(13.6.2)

Отсюда

следует,

что

1 -

ф(

и),

дополнение

до

вероятности

разорения,

можно

интер

претировать

как

функцию

распределения

С.в.

частности,

1 -

ф(О)

= P(L:::;

О)

P(L=

О),

(13.6.3)

(13.6.4)

поскольку

О.

этом

случае

максимальные

потери

происходят

момент

t =

О.

Кроме

того,

распределение

с.в.

является

распределением

смешанного

типа.

точ

ке

сосредоточен

«сгусток.

вероятностной

массы

l-ф(О),

остальная

масса

непре

рывно

распределена

там,

где

С.В.

принимает

положительные

значения.

Основной

результат

этого

раздела

явная

формула

для

производя

щей

функции

моментов

С.в.

которая

силу

равенства

(13.6.2)

может

использо

ваться

для

получения

информации

Феи).

Теорема

13.6.1.

И.меет

.место

равенство

А1

ОРI

L(r) =

(1+0)plr-A1x(r)

Эквивалентным

является

равенство

8 8

А1

(Т)

- +

-----=---....:........:.--=----

L -

1+0

1+01+(1+0)PI

X(T)'

(13.6.4А)

ИЗ

которого

наличие

«сгустка.

вероятностной

массы

нуле

видно

более

явно,

так

как

вклад

вероятности

при

L =

О в

производящую

функцию

моментов,

согласно

формуле

(13.5.2),

равен

1 -

ф(О)

= 1

Заметим,

что

уравнение,

использовавшееся

для

получения

коэффициента

Лундбер

га,

получено

приравниванием

знаменателя

правой

части

равенства

(13.6.4)

нулю.

Доказательство.

доказательстве этой

теоремы

используются

моменты

вре

мени,

когда

процесс

суммарных

потерь

достигает

новых

рекордных

значений.

Ти

пичная

реализация

процесса

суммарных

потерь

ноказана

на

рис.

13.6.1.

На

этой

реа

лизации

новые

рекордные

значения

отмечаются

трижды.

После

каждого

рекордного

значения

вероятность

того,

что

оно

не

будет

превзойдено,

равна

1 -

ф(О).

Вероят

ность

того,

что

оно

будет

превзойдено,

равна

ф(О).

этом

утверждении

мы

осно

вываемся

на

том

факте,

что

сложный

пуассоновский

процесс

имеет

стационарные

независимые

приращения.

Если

рекорд

превзойден,

то

функция

плотности

величины

превышения

сов

падает

функцией

плотности

С.в.

которая

определена

соотношением

(13.5.3).

372

Гл.

13.

Модели

коллективных

рисков

на

дЛительном

интервале

времени

1з

---------------

-----~

L L

t ----, ,

,~------------~~---.

Рис.

13.6.1.

Типичная

реализация

процесса

суммарных

потерь

Рис.

13.6.1

показывает,

что

мы

можем

представить

с.в.

как

сумму

случайного

числа

случайных

величин, а

именно,

(13.6.5)

Здесь

N -

число

новых

рекордных

величин,

имеющее

геометрическое

распределе

ние,

определяемое

вероятностями

(

)

n+l

P(N

=n) =

'Ф(О»)['Ф(О)]n

1':

(}

n =

0,1,2,

....

(13.6.6)

Производящая

функция

моментов

этого

распределения

имеет

вид

(}

MN(r) = 1

(}

+ - e

(13.6.7)

Случайные

величины

N,L

••.

взаимно

независимы

общая

плотность

С.в.

задается

соотношением

(13.5.3).

Согласно

формуле

(12.2.7),

производящая

функция

моментов

С.в.

имеет

вид

ML(r) =MN[ln MLl

(Т)]

= 1 +8 _ MLl

(Т)

формуле

(13.5.4)

функция

(Т)

выражена

через

МХ(Т)

и,

таким

образом,

ВРlТ

ML(r) = 1+

- [lj(plr)][Mx(r) -

В)РlТ

МХ(Т)'

что

нужно

было

показать.

Проверка

другой

формулы,

(13.6.4А),

сводится

алге

браическим

выкладкам.

•

Заметим,

что,

поскольку

1 -

'Ф(u)

является

функцией

распределения

с.в.

[см.

(13.6.2)],

которая

имеет

4:СГУСТОК.

вероятностной

массы

начале

координат

непре

рывное

распределение

массы

для

положительных

значений

и,

100

ML(r) =

11'(0)

еur[-'Ф'(u»)du

(}

еur[-'Ф'(u»)du.

Поэтому

из

соотношения

(13.6.4А)

следует,

что

(ОО

еur[_'Ф'(u»)

В[МХ(Т)

1+B1+(1+(})Pl

Х(Т)'

(13.6.9)

13.6.

Максимальные

суммарные

потери

373

Эту

формулу

можно

использовать

для

некоторых

семейств

распределений

страхо

вых

выплат,

чтобы

находить

явные

выражения

для

'Ф(

и).

Одно

такое

семейство

образуют

смеси

показательных

распределений

вида

Р(Х)

= L

Аifiiе-,в,х,

i=1

О.

(13.6.10)

f3i

О,

+... +

= 1.

этом

случае

f3i

(Т)

= L A

р.

_r .

i=1

(13.6.11)

Первоначально

величина

МХ(Т)

определялась

как

некоторое

математическое

ожи

дание.

Оно

существует,

только

если

r < , =min{fil,'"

,.вn}'

Однако

эту

функцию

можно

естественным

образом

продолжить

на

все

значения

fJi.

Для

простоты

за

писи

для

этого

продолжения

мы

будем

использовать

тот

же

самый

символ

МХ(Т).

Подставим

выражение

(13.6.11)

(13.6.9)

заметим,

что

правая

часть

получае

мой

результате

этой

подстановки

формулы

оказывается

рациональной

функцией

от

Т,

которую,

используя

метод

разложения

на простые

дроби,

мы

можем

переписать

виде

eM[-,р'(u)]

То

~OT

. (13.6.12)

Единственная

функция,

которая

удовлетворяет

этому

соотношению

ф(оо)

О,

имеет

вид

ф(и)

= L

Cie-

riu

• (13.6.13)

i=l

Значит,

этим

выражением

задается

вероятность

разорения.

Мы

проиллюстрируем

описанную

процедуру

двумя

примерами.

Пример

13.6.1.

Выведем

выражение

для

'Ф(и)

если

С.в.

имеют

показатель

ное

распределение.

Другими

словами,

равенстве

(13.6.10)

выбирается

n = 1.

Решение.

Поскольку

МХ(Т)

= - ,

- r

РlТ

правая

часть

равенства

(13.6.9)

имеет

вид

1 0[1/(1 -

Рl

)

Тl

1+01+(1+0)Р1т-1/(1-Р1Т)

1+00-(1+0)Р1Т

Т1-

где

1/(1

В)

Т1

В/[(1

В)Р1],

Итак,

ф(и)

= C

r1U

•

Эта

формула

была

ранее

выведена

примере

13.4.4

(формула

(13.4.8».

Пример

13.6.2.

Вычислим

-ф(u)

при

условии,

что

()

2/5

что

р(х)

задается

соотношением

3 7

р(х)

= 2

е-ЭХ

е-

7х

О.

Решение.

Воспользовавшись

указанным

выражением

ДЛЯ

р(х),

получаем

МХ(Т)

3/2

7/2

З-r

7-т

1 1 1 1 5

Р1=-'-+-'-=-

2 3 2 7

21'

374

Гл.

13.

Модели

коллективных

рисков

на

длительном

интервале

времени

Подставляя

эти

выражения

правую

часть

формулы

(13.6.9)

проводя

упрощения,

получаем

6 5 -

7 6

-7т

•

Знаменатель

имеет

корни

Т1

= 1

Т2

= 6.

Следовательно,

это

выражение,

перепи

санное

форме

правой

части

формулы

(13.6.12),

равно

6С

--+

l-т

6-т

подсчитываем

коэффициенты:

= 24/35

02 =

1/35.

Таким

образом,

()

-и

-6и

'I/J

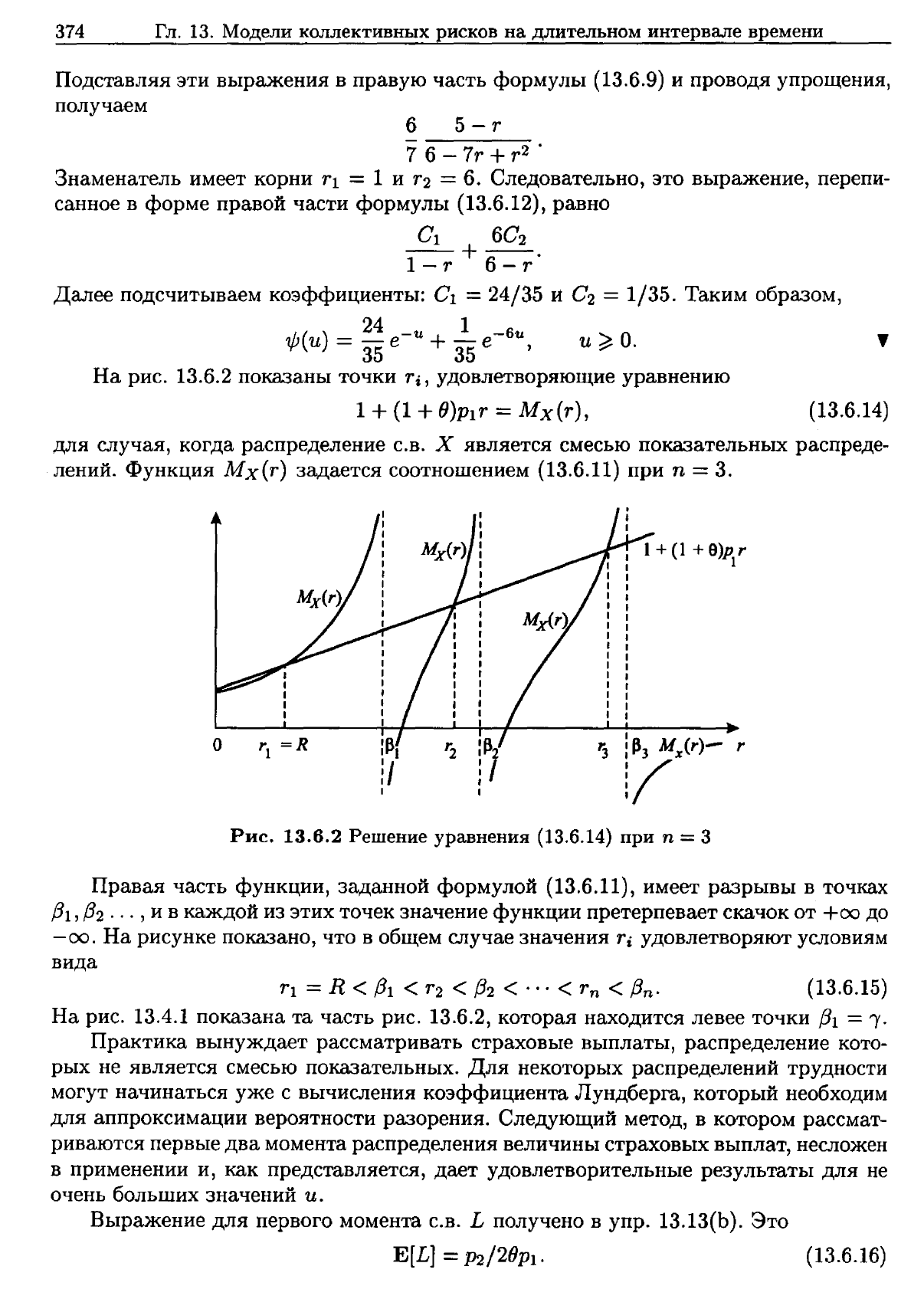
На

рис.

13.6.2

показаны

точки

Ti,

удовлетворяющие

уравнению

О)РIТ

МХ(Т),

(13.6.14)

для

случая,

когда

распределение

с.в.

является

смесью

показательных

распреде

лений.

Функция

МХ(Т)

задается

соотношением

(13.6.11)

при

n = 3.

8)р

Рис.

13.6.2

Решение

уравнения

(13.6.14)

при

n =3

Правая

часть

функции,

заданной

формулой

(13.6.11),

имеет

разрывы

точках

(31,

(32

...

каждой

из

этих

точек

значение

функции

претерпевает

скачок

от

+00

до

00.

На

рисунке

показано,

что

общем

случае

значения

удовлетворяют

условиям

вида

тl

= R <

(31

Т2

(32

< ... <

(3n.

(13.6.15)

На

рис.

13.4.1

показана

та

часть

рис.

13.6.2,

которая

находится

левее

точки

(31

Практика

вынуждает

рассматривать

страховые

выплаты,

распределение

кото

рых

не

является

смесью

показательных.

Для

некоторых

распределений

трудности

могут

начинаться

уже

вычисления

коэффициента

Лундберга,

который

необходим

для

аппроксимации

вероятности

разорения.

метод,

котором

рассмат

риваются

первые

два

момента

распределения

величины

страховых

выплат,

несложен

применении

и,

как

представляется,

дает

удовлетворительные

результаты

для

не

очень

больших

значений

Выражение

для

первого

момента

с.в.

получено

упр.

13.13(Ь).

Это

E[LJ =

Р2/

Р1.

(13.6.16)

13.7.

Замечания

литература

375

Далее,

из

формулы

(13.5.2)

следует,

что

ф(О)

1/(1

+8),

а из

(13.4.5) -

что

ф(u)

Мы

предлагаем

приближение

и>

О,

где

выбирается

таким

образом,

чтобы

приближенное

значение

величины

E[L]

равнялось

значению,

которое

задается

соотношением

(13.6.16).

Но

(Х>

1 1

E[L] = J

[1-FL(U)]dU~1+8К'

так

что

2fJPl

В)Р2

дает

нам

требуемое

равенство.

Таким

образом,

наша

аппроксимация

это

"-J

1 [ 28pl

]

ф(

и)

= 1 +8

ехр

8)Р2'

О.

Заметим,

что

если

распределение

страховых

выплат

является

показательным

со

средним

Pl,

так

что

Р2

2p~,

то

результат

точен:

см.

(13.4.8).

Этот

метод

обоб

щается

упр.

13.19,

где

дается

уточненная

аппроксимация.

13.7.

Замечания

литература

Важная

роль

совместного

распределения

времени

разорения

величины

рис

кового

резерва

непосредственно

после

разорения

(Т)

дЛЯ

процесса

рискового

ре

зерва,

котором

суммарные

страховые

выплаты

описываются

сложным

пуассонов

еким

процессом, явствует

из

структуры

знаменателя

выражении

для

вероятности

разорения

теореме

13.4.1.

Возможность

выразить

вероятности

разорения

для

та

кого

процесса

рискового

резерва

через

распределение

величины

страховых

выплат

демонстрируется

теоремах

13.5.1

13.6.1.

момента

выхода

свет

первого

издания

книги

«Актуарная

математика»

был

опубликован

ряд

результатов

этой

области.

Недавняя

работа

[Gerber, Shiu 1998]

дает

дос'rупный

обзор

этих

результатов.

Мы

процитируем

резюме

этой

работы:

работе

исследуется

совместное

распределение

момента

разорения,

величины

рискового

резерва

непосредственно

перед

разорением

дефицита

момент

разоре

ния.

Классическая

модель

обобщается

введением

дисконтирования.

Мы

показываем,

как

вычислять

математическое

ожидание

дисконтированных

штрафов,

назначае

мых

момент

разорения

зависящих

от

величины

дефицита

момент

разорения

размера

резерва

непосредственно

перед

разорением.

Математические

ожидания

дис

контированных

штрафов,

рассматриваемые

как

функции

начальной

величины

рис

кового

резерва,

удовлетворяют

определенному

уравнению

восстановления,

которое

обладает

вероятностной

интерпретацией.

Для

нулевых

очень

больших

начальных

резервов,

также

случае

показательного

распределения

величины

выплат

про

извольного

начального

резерва

получены

явные

выражения.

Мы

обобщаем

формулу

Диксона,

которая

выражает

совместное

распределение

рискового

резерва

непосред

ственно

перед

разорением

момент

разорения

через

вероятность

разорения

за

бесконечное

время.

Явные

выражения

получены

также

случае,

когда

дивиденды

выплачиваются

соответствии

барьерной

стратегией.

Читатель,

ознакомившийся

доказательством

теоремы

13.5.1,

поймет,

что

этом

доказательстве

использовался

метод

штрафной

функции,

заимствованный

из

этой

статьи.

376

Гл.

13.

Модели

коллективных

рисков

на

длительном

интервале

времени

По

этим

вопросам

рекомендуются

следующие

книги:

• [Beard, Pentikainen,

Ревопеп

1984],

• [Beekman 1974],

• [Biihlmann 1970],

• [Gerber 1979],

• [Panjer, Willmot 1992],

• [Seal 1969].

Теория

разорения

развивалась

скандинавской

(Лундберг,

Крамер)

итальянской

(Де

Финетти)

школами.

Эти

исследования

подробно

описаны

книге

[Dubourdieu

1952J.

МЫ

не

обсуждали

знаменитую

асимптотическую

формулу

для

вероятности

ра

зорения

-t

00,

(13.7.1)

где

С -

некоторая

констан'га.

Учитывая

теорему

13.4.1,

эту

формулу

легко

понять:

она

означает,

что

величина,

обратная

знаменателю

формуле

(13.4.4),

имеет

пре

дел

при

-t

00,

равный

константе

из

правой

части

формулы

(13.7.1).

Для

случая,

когда

распределение

величины

страховых

выплат

смесь

показательных,

это

асим

птотическое

представление

иллюстрируется

соотношением

(13.6.13).

Соотношение

из

упр.

13.11

называется

дефектным

уравнением

восстановления.

Решение

уравнений

этого

типа

обсуждались

Феллером

[Feller 1966].

частности,

он

доказал

формулу

(13.7.1).

Используя

такую

же

технику,

Гербер

[Gerber 1974]

нашел

предел

условного

распределения

с.в.

-и

(Т)

при

условии

при и

-t

00.

Если

МЫ

усложним

модель,

предположив,

что

на

рисковый

резерв

начисляют

ся

проценты

постоянной

интенсивностью

О,

ТО

интегро-

дифференциальном

уравнении

(lЗ.А.12),

приведенном

приложении

настоящей

главе,

нам

надо

заме

нить

множитель

на

дu.

Если

страховые

выплаты

имеют

показательное

распре

деление,

то

это

модифицированное

уравнение

допускает

явное

решение

терминах

гамма-функции.

Если

роли

премий

выплат

поменять

местами,

т.

е.

если

премии

представляют

собой

выплаты,

произво,а,имые

страхОВЩИКОМ,

выплаты

делаются

пользу

стра

ховщика,

так

что

U(t)

+S(t),

предполагается,

что

ЛР1,

то

существует

явная

формула:

ф(u)

Чтобы

ее

доказать,

нужно

установить

результат,

аналогичный

теореме

13.4.1,

за

метить,

что

резерв

момент

разорения

обязательно

равен

О.

Предлагалось

исполь

зовать

эту

модель

при

рассмотрении

портфеля

аннуитетов,

когда

вследствие

смерти

освобождается

резерв

страхователя

возникает

отрицательная

выплата.

Сил

[Seal1978b]

рассматривал

численные

методы

для

определения

вероятности

разорения

за

конечное

время.

работе

[Beekman, Bowers 1972]

аппроксимация

для

ф(u,

построена

помощью

уравнивания

моментов.

Гербер

[Gerber 1974]

Де

Виль

дер

[Ое

Vylder 1977]

нашли

верхние

границы

для

ф(u,

t),

применяя

мартингальные

методы.

Панджер

Виллмот

[Panjer, Wi1lmot 1992, Chap.

11]

рассматривали

вопросы,

затронутые

настоящей

главе,

применяя

более

сложные

математические

методы.

Приложение

377

Разделы

11.4

11.5

их

книги представляют

особый

интерес,

поскольку

них

разви

ваются

рекуррентные

методы

приближенного

вычисления

вероятностей

разорения

за

бесконечное

время.

Приложение

Доказательство

теоремы

13.2.2.

Следующие

вычисления

приводят

простой

ре

куррентной

формуле

для

модифицированного

рискового

резерва:

......

а а

-1--

Ui-l

- Wi -

-1--

Wi = Ui-l +

-1--

-а

......

у;.

Ui-l

-1-(Yi

aWi-l)

Ui-l

-1-'-,

i =

1,2,...

(13.А.l)

-а -а

Из

формул

(13.А.l),

(13.2.18)

из

независимости

с.в.

следует,

что

для

любого

Е[ехр(

-Л[U

Иi])]

Рассмотрим

теперь

тождество

i =

0,1,

...

(13.А.2)

Е[ехр(

-лип)]

= L

E[exp(-НО

)

IT=

P(T=i)+E[exp(-ЛИ

)

Р(Т

>n).

(13.А.3)

i=l

Из

формулы

(13.А.2)

дЛЯ

i =

вытекает,

что

выражение

левой

части

равенства

(13.А.3)

равно

ехр(

ЛИп).

правой

части

мы

заменяем

суммой

(О

Иi).

Разность

не

зависит

от

...

Иi.

Это

можно

проверить,

воспользовавшись

формулой

(13.А.l)

независимостью

с.в.

Yi,

частности,

с.в.

fJi

не

зависит

от

события

f =

Из

(13.А.2)

следует,

что

Е[ехр(

-RfJn)

[Т=

Е[ехр(

-лfJ

)

IT= i].

Поэтому

равенство

(13.А.3)

можно

переписать

виде

ехр(

-Ни)

= L

Е[ехр(

-лип)

Т=

Р(Т=

i) +

Е[ехр(

-лип)

Р(Т

>n);

(13.А.4)

i=l

оно

аналогично

равенству

(13.А.8)

приведенном

ниже

доказательстве

теоремы

13.4.1.

Теперь

положим

00.

Первое

слагаемое

правой

части

формулы

(13.А.4)

сходится

E[exp(-НUn)

17'=

P(T=i)

E[exp(-ЛUт)

00]

Р(Т

<00).

i=l

Таким

образом,

чтобы

завершить

доказательство

теоремы

13.2.2,

нам

надо

показать,

что

второе

слагаемое

правой

части

формулы

(13.А.4)

стремится

нулю

при

00.

Мы

проведем

эту

проверку

следующим

образом.

Из

равенства

(13.2.17)

следует,

что

Е[8

]

= n

Е(У]

-а

1-а

(Е[У]

-w).

1-а

Поскольку

с>

E[Y]j(1

а),

найдется

положительное

число

0',

такое,

что

Е[Иn]

о:n,

если

достаточно

велико.

Далее,

из

равенства

(13.2.17)

следует,

что

найдется

такое

число

{32,

что

D[U

]

(32

Завершение

проверки

того,

что

второе

слагаемое

правой

части

формулы

(13.А.4)

стремится

нулю

при

00,

аналогично

доказательству,

которое

будет

приведено

деталях

для

второго

слагаемого

правой

части

равенства

(13.А.8)

при

доказательстве

теоремы

13.4.1

ниже.

Подробное

доказательство

этого

шага

можно

найти

также

работе

Промислова

[Promislov

1991а].

•

Доказательство

теоремы

13.4.1.

Для

t >

r >

рассмотрим

E[e-rU(t)]

E[e-rU(t)

Р(Т ~

E[e-rU(t)

Р(Т

t).

(13.А.5)

Поскольку

U(t)

S(t),

выражение

левой

части

равно

ехр{

-тu

- rct +

лt[Мх(r)

- 1]}.

(13.А.6)

378

Гл.

13.

Модели

КОJ!.лективных

рисков

на

длительном

интервале

времени

первом

слагаемом

правой

части

записываем

U(t) =

U(Т)

+ [U(t) -

И(Т)]

U(Т)

+c(t -

Т)

- [S(t) -

В(Т)].

Для

заданной

с.в.

выражеиие

квадратных

скобках

не

зависит

от

U(Т)

имеет

слож

ное

пуассоновское

распределение

пуассоновским

параметром

л(t

Т).

Поэтому

первое

слагаемое

правой

части

формулы

(13.А.5)

можно

переписать

следующим

образом:

Е[ехр(

-тU(Т))

ехр(

-7'C(t -

Т)

л(t

Т)[МХ

(Т)

1]}

Р(Т

t).

(13.А.7)

Выражения

(13.А.6)

(13.А.7)

можно

существенно

упростить,

если

выбрать

таким

обра

зом,

что

-те

>'[Мх(т)

О.

этого

уравнения

имеется

два

решения

(см.

рис.

13.4.1).

Решение

О,

подставленное

(13.А.5),

приводит

тривиальному

тождеству.

Второе

решение

r =R

является

коэффици

ентом

Лундберга.

Если,

выбрав

подставить

полученные

упрощенные выражения

(13.А.5),

то

мы

придем

равенству

Е[е

-RU(T)

Р(Т

E[e-RU(t)

Р(Т

>t).

(13.А.8)

Пусть

теперь

t -+

00.

Первое

слагаемое

правой

части

сходится

E[e-RU(T)

оо]Ф(u).

Теорема

13.4.1

будет

доказана,

если

мы

покажем,

что

второе

слагаемое

правой

части

стремится

нулю

при

00.

Мы

сделаем

это

следующим

образом.

Пусть

а:

ЛРl,

р2

>'Р2.

Тогда,

согласно

формулам

(13.3.6)

(13.3.7), E[U(t)] =

Е[и

+et - S(t)] =u +at

D[U(t)] = D[S(t)] =

f32

Рассмотрим

выражение

u +

a:t

f3е/

которое

положительно

для

достаточно

больших

Расщепим

теперь

второе

слагаемое

правой

части

равенства

(13.А.8)

на

два,

первом

из

которых

U(t)

больше

u +

a:t

f3t

во

втором

меньше.

Используя

неравенство

Чебышёва,

мы

получим

E[e-RU(t)

Т>

U(t)

u +

a:t

f3t

Р[Т

>t,

U(t)

u + a:t -

f3t

]

E[e-RU(t)

>t, U(t) >

a:t

,8t

]

Р[Т

>t, U(t) >

,ве/

]

P[U(t)

a:t

,ве/

]

exp[-R(u

a:t

- Pt

)]

exp[-R(u

a:t

,8t

)].

Но

из

этой

верхней

границы

очевидно,

что

второе

слагаемое

правой

части

(13.А.8)

стре

мится

нулю

при

00.

•

Доказательство

теоремы

13.5.1.

Для

этого

доказательства

мы

введем

новое

ПОНЯ

тие,

которое

представляет

самостоятельный

интерес.

Пусть

ш(х),

О,

функция,

такая,

что

(х)

О.

Положим

ф(u;

ш)

Е[ш(U(Т»

оо]Ф(u),

(13.А.9)

рассматривая

эту

величину

как

функцию

начального

рискового

резерва

Мы

можем

интерпретировать

ш(х)

как

штраф,

если

величина

резерва

момент

разорения

равна

х.

этом

случае

величина

1/;(

и;

ш)

представляет

собой

математическое

ожидание

величины

штрафа.

Приведем

такие

примеры:

(а)

если

ш(х)

'.го

из

формулы

(13.4.4)

следует,

что

'Ф(Uj

;

(Ь)

если

ш(х)

= 1,

то из

формулы

(lЗ.А.9)

следует,

что

ф(U;W)

'Ф(u);

(с)

если

то

Wh(X)

{1,

О,

-h,

-h

О,

1/;(0;

Р[U(Т)

< - h I

оо]ф(О).

Мы

начнем

доказательство

того,

что

покажем,

что

для

любой

ограниченной

функции

ш(х)

>'100

'Ф(Оj

ш)

= - w(

-y)[l

р(у)]

dy.

(13.А.10)

Приложение

379

Применяя

формулу

полной

вероятности

условному

математическому

ожиданию

штра

фа

(13.А.9)

при

условии,

выраженном

терминах

числа

страховых

случаев

начальном

интервале

(О,

Ь),

мы

получим

1jI(UjW)

Р[N(Ь)=О]{условное

математическое

ожидание

штрафа

при

условии

N(b)=O}

+P[N(b) =

l]{условное

математическое

ожидание

штрафа

при

условии

N(b) =

+P[N(b)

>l]{условное

математическое

ожидание

штрафа

при

условии

N(b) >

1}.

(13.А.ll)

Из

свойств

пуассоновского

считающего

процесса

следует,

что

P[N(b) =0] =

е-

АЬ

P{N(b) =

лЬе-

АЬ

P[N(b) >

ЬА(Ь),

где

предел

А(Ь)

равен

при

-t

О.

Поскольку

мы

предполагаем,

что

w(x)

является

неотрицательной

ограниченной

функцией,

lIIайдется

такое

М,

что

х)

М.

Принимая

во

внимание

это

ограничение

свойства

сложного

пуассоновского

процесса,

мы

можем

действовать

следующим

образом.

Для

N(b) =

условное

математическое

ожидание

штрафа

равно

ф(U+СЬ;

w).

Посколь

ку

страховых

случаев

не

происходило

премиальный

доход

поступал

интенсивностью

с,

рисковый

резерв

достиг

значения

и+сЬ

стационарные

независимые

приращения

приводят

процесс

новой

начальной

точке.

Для

N(b) = 1

нам

необходимо

рассмотреть

несколько

случаев

зависимости

от

вели

чины

х,

отдельной

страховой

выплаты.

•

Если

и,

ТО

рисковый

резерв

остался

положительным

и,

как

случае

отсут

ствия

страховых

выплат, условное

математическое

ожидание

штрафа

равно

ф(

u +

сЬ

- Xjw).

•

Если

u <

u +

сЬ,

достаточно

заметить,

что

условное

математическое

ожидание

штрафа,

обозначим

его

через

(Х,

Ь),

не

превосходит

верхней

грани

для

(х

именно

М.

•

Если

> u +

сЬ,

то

рисковый

резерв

становится

отрицательным

момент

страховой

выплаты

условное

математическое

ожидание

штрафа

равно

w(u +

Х),

где

величина

поступлений,

полученных

до

момента

страховой

выплаты.

Таким

образом,

для

N(b) = 1

условное

математическое

ожидание

штрафа

равно

Г~

ф(u

сЬ

Х;

w)p(X) dx +

сь

А(х,

b)p(x)dx

100

w(u +

х)р(х)

dx.

Jo u

и+сЬ

Для

N(b) > 1

также

достаточно

заметить,

что

условное

математическое

ожидание

штрафа,

обозначим

его

(Ь

не

превосходит

М,

верхней

грани

дЛЯ

Подставляя

эти

три

варианта

(13.А.11),

мы

получим

ф(U;

-»ф(u

сЬ;

>.Ье->Ь

[L"

ф(u

сь

х;

w)p(x)

ах

1"+'·

А(х,

Ь)р(х)

ах

(ОО

w(u +

х)р(х)

dx] +bA(b)D(b).

(13.А.12)

Ju+cb

Вычтем

теперь ф(

и;

из

обеих

частей

формулы

(13.А.12)

разделим

полученное

равен

ство

на

сЬ.

Мы

получим

АЬ

Ф(U+СЬjw)-1/J(UjW)

-АЬ[l

,,,,,(

)

()d

СЬА

(

Ь)

()d

+-е

'f'u+c

-ХjWРХ

Х+

Х,

рх

100

ш(и

Х)Р(Х)

dX]

А(ь)п(ь)

О.

(13.А.13)

и+сЬ

(13.А.14)

380

Гл.

13.

Модели

коллективных

рисков

на

длительном

интервале

времени

При

пределы

трех

слагаемых

(13.А.13)

равны

->'-ф(иj

ю)

с-ф'(и;

[J:U

-ф(и

Х;

w)p(X) dx +

lOO

w(u

х)р(х)

dx]

О.

Таким

образом,

/.U

>'100

ф'(и;w)

--ф(u;w)

- -

-ф(u-х;w)р(х)dх-

w(u-x)p(x)dx.

с с

Проинтегрируем

ЭТО

уравнение

по и

от

до

Получающиеся

при

этом

двойные

интегра

лы

могут

быть

сведены

одинарным

заменой

переменных.

первом

двойном

интеграле

заменим

и и

на

х и

х.

Тогда

{Z-1I

ф(и-Хjw)р(х)dхdи=

ф(у;w)p(x)dxdy

~(у;w)Р(z-у)dу.

Во

втором

двойном

интеграле

заменим

и и на

Получаем

[00

(ОО

[1I+z

[00

w(u

х)р(х)

dx du =

111

-у)р(х)

dx dy =J

-у)[Р(у

Р(у»)

dy.

Таким

образом,

равенство

(13.А.14),

будучи

проинтегрированным

от

дО

дает

>'1%

/.00

~(ZjW)-ф(О;w)

= -

ф(у;w)[I-Р(z-у»)dу--

w(-у)[Р(у+z)-Р(у»)dу.

(13.А.15)

При

первые

слагаемые

обеих

частях

пропадают

остается

100

-Ф(О;w)

w(-y)(I-

P(y»)dy.

Пусть

теперь

функция

Wh(X)

определена,

как

примере

(с).

Это

значцт,

что

()

{

-h,

О,

-h

О.

Тогда

>'100

Р[И(Т)

< - h I

оо]ф(О)

ф(Оj

Wh)

= -

Р(у)]

dy.

Следовательно,

при и

вероятность

того,

что

рисковый

резерв

какой-либо

момент

ока

жется

меньше

нуля

примет

значение

между

-h

- dh,

равна

(>./с)[l-

P(h)]

dh.

Если

О,

то событие,

состоящее

том,

ЧТО

рисковый

резерв

какой-либо

момент

окажется

меньше

и и

примет

значение

между

- h

и и

- h - dh,

имеет

такую

же

вероятность.

Это

доказывает

теорему

13.5.1. •

Упражнения

разделу

13.2

13.1.

Предположим,

что

С.В.

принимает

только

два

значения,

что

P(W

=0)

р,

P(W=2)

где

+ q = 1.

Предположим,

что

= 1,

1/2

что

целое.

Определите

этом

случае

(а)

И(Т),

(Ь)

-ф(и)

терминах

Н,

(с)

терминах

р,

(d)

-ф(и)

терминах

р,

13.2.

Рассмотрим

страховые

случаи

периоды

n+2,

...

n+т

обозначим

через

Вn,т

их

общее

число.

Таким

образом,

Вn,т

= W

+... +W

Величина

страховых

выплат дЛя

каждого

периода

порождается

случайным

процессом,

опи

санным

(13.2.14).

Проверьте,

что

m-i

m m 1

m-i+1

т+1

~"~

-а

а-а

(а)

Вn,т

L..J

)

~a'

L..J

Yn+i +

'о

'1"1

з=