Бауэрс Н., Гербер Х., Джанс Д., Несбитт С., Хикман Дж. Актуарная математика
Подождите немного. Документ загружается.


10.5.
Сопутствующие
таблицы
выбытия
по
единственной
причине
С
другой
стороны,
если
с.в.
Тl
(х)
И
Т2(Х)
зависимы,
то
I-l~Т)(t)
= -
~
InSTl,T2(t,t):f. -
~
ln
ВТl,Т2
(t,O) -
~
lnSTl,T2(0,t).
291
(10.5.14)
Два
слагаемых
в
правой
части
равенства
(10.5.13)
называются
.маргинальными
и'Н
mеНСU6носm.я.мu
6'Ыбъtmи.я,
ассоциированными
с
соответствующими
с.в.
Т
1
(х)
и
Т
2
(х).
Если
Т
1
(х)
и
Т
2
(х)
независимы,
то
маргинальные
интенсивности
выбытия
из
модели
выбытия
по
единственной
причине
могут
быть
использованы
вместе
с
ра-
венством
(10.5.2)
для
получения
tP~T).
Если
с.в.
Т
1
(х)
И
Т
2
(х)
зависимы,
то
нет
ни
какой
уверенности,
что,
предполагая
выполненным
равенство
(10.5.2),
мы
получим
функцию
дожития
для
случайной
величины
продолжительности
периода
времени
до
выбытия
в
модели
выбытия
по
нескольким
причинам
.
Пример
10.5.2.
Этот
при
мер
основывается
на
примерах
9.2.1, 9.2.2
и
9.3.1.
Пусть
зависимые
с.в.
Т
1
(х)
И
Т
2
(х)
имеют
такую
совместную
функцию
плотности:
f
( )
-
{О'ООО6(В
- t)2,
О
< S < 10,
О
< t < 10,
Тl,Т2
В,
t -
О
в
противном
случае.
Совместная
функция
дожития
построена
в
примере
9.2.2,
а
функция
дожития
для
с.в.
Т
= min[T
1
,
Т
2
]
получена
в
при
мере
9.3.1.
Покажем,
что
d d d
- dt
InsT(t):f.
- dt ln
ВТ
1
,Т
2
(t,O) - dt lnST
1
,T
2
(0,t).
Решение.
Имеем
и
d 4
--d
ln 8T(t) =
О
'
t 1 - t
0<
t < 10,
_
~
ln s t _ 4 1 200 -
БОt
+
бt
2
dt
т(
) -
10
- t
:f.
10 - t 50 - 5t + t
2
При
мер
10.5.3.
Этот
при
мер
основан
на
примерах
9.2.3
и
9.3.2.
Независимые
С.В.
Т
1
(х)
И
Т
2
(х)
имеют
совместную
функцию
плотности
fT
1
,T2
(В,
t) = [0,02(10 - 8)][0,02(10 - t)],
Покажем,
что
о
< 8 < 10,
О
< t < 10.

292
Гл.
10.
Модели
выбытия
по
нескольким
причинам
Решение.
Функция
дожития
С.в.
Т
= min[T
1
(х),
Т
2
(х)]
построена
в
примере
9.3.2.
Следовательно,
0<
t < 10,
о
< t < 10,
0<
t < 10.
Значит,
и из
соображений
симметрии
d 2
-
dt
InST1,T
2
(0,
t) = 10 -
t'
d d d
-
dt
InsT(t)
= - dt
InST
1
,T
2
(t,
0)
- dt
InST
1
,T
2
(0,t).
'f
Интересным,
но
обескураживающим
аспектом
примеров
10.5.2
и
10.5.3
являет
ся
то,
что две
зависимые
случайные
величины
продолжительности
периода
времени
до
момента
выбытия
и
две
аналогичные
независимые
случайные
величины
дают
одно
и то
же
распределение
с.в.
Т
= min[T
1
(x),T
2
(x)].
Значения
Т
можно
наблю
дать,
но
без
дополнительной
информации
невозможно
решить,
какая
из
этих
двух
моделей
лежит
в
основе
наблюдаемых
значений.
Как
и
в
разд.
9.3,
это
-
пример
невозможности
идентификации.
Далее
в
настоящей
главе
при
построении
распре
делений
в
модели
с
несколькими
причинами
выбытия,
исходя
из
распределений
в
сопутствующих
моделях
с
единственной
причиной
выбытия,
будет
предполагаться,
что
случайные
величины
из
этих
сопутствующих
моделей
независимы.
Замечание.
Нам
может
помочь
сравнение
модели
страхования
для
нескольких
лиц
и
модели
выбытия
по
нескольким
причинам
,
но
эти
модели
не
эквивалентны.
Основное
различие
заключается
в
двух
фактах,
которые
отмечались
при
обсужде
нии
формулы
(10.5.2)
и
в
примере
10.5.2.
В
одной
модели
можно,
по
крайней
мере
теоретически,
наблюдать
обе
случайные
величин
Т(х)
и
Т(у),
в
то
время
как
в
дру
гой
наблюдается
только
минимум
ИЗ
двух
С.в.
Т
1
(х)
И
Т
2
(х)
,
а
также
то,
на
какой
из
этих
двух
случайных
величин
этот
минимум
достигается.
Соответствующая
пробле
ма
в
оценивании
модели
страхования
для
нескольких
лиц
упоминалась
в
разд.
9.3.
Кроме
того,
limt-+oo
tPx
=
limt-+oo
tPy
=
О,
но
нет
никаких
гарантий,
что
Нm
tpl(j)
=
О
j =1,2.
t---+oo
х
,
10.6.
Построение
таблиц
выбытия
по
нескольким
причинам
При
построении
модели
выбытия
по
нескольким
причинам
лучше
всего,
если
для
непосредственной
оценки
вероятностей
q~j)
можно
использовать
различные
данные,
включая
данные
о
возрасте
и
причинах
выбытия
в
исследуемой
совокупности.
Боль
шие,
хорошо
обоснованные
пенсионные
схемы
для
работающих
располагают
такими
данными.
В
других
системах
такие
данные
часто
недоступны.
Другой
возможностью
является
построение
модели
на
основе
коэффициентов
выбытия
из
сопутствующих
моделей
с
единственной
причиной
выбытия,
которые,
как
предполагается,
адекват
но
описывают
изучаемую
совокупность.
Адекватность
такой
модели
следует
затем
проверить
с
помощью
данных,
которые
становятся
известными.
Если
подобраны
подходящие
сопутствующие
таблицы
выбытия
по
единственной
причине,
то
для
завершения
построения
таблиц
выбытия
по
нескольким
причинам

10.6.
Построение
таблиц
выбытия
по
нескольким
причинам
293
можно
использовать
результаты
разд.
10.5.
Если
известны
р~(Л
для
j = 1,2,
...
,
т
и
всех
значений
х,
то
можно
подсчитать
p~T),
пользуясь
формулой
(10.5.2),
и
q~T),
пользуясь
формулой
q~T)
= 1 -
p~T).
Остается
разбить
q~T)
на
компоненты
q~j)
для
j =
1,2,
...
,
т.
Если
в
модели
принято
предположение
о
постоянстве
интенсивности
выбытия
или
о
равномерности
распределения
моментов
выбытия,
то
для
вычисле
ния
величины
q~j)
может
быть
использована
формула
(10.5.9).
Пример
10.6.1.
Используем
формулы
(10.5.2)
и
(10.5.9)
для
получения
таблицы
выбытия
по
нескольким
причинам
,
соответствующей
абсолютным
коэффициентам
выбытия,
заданным
ниже.
Предположительно
актуарий
исследовал
характеристики
группы
участников
и
решил,
что
сопутствующие
таблицы
выбытия
по
единствен
ной
причине
являются
подходящими
для
изучаемой
СОВОКУПНОСТИ.
Предполагается
также,
что
причина
3
является
выходом
на
пенсию,
что
может
происходить
между
возрастами
65
и
70
лет,
а
в
70
лет
происходит
обязательно.
х
1(1 )
'(2)
1(3)
ЧХ
qж
ЧХ
65
0,020 0,02 0,04
66 0,025
0,02 0,06
67
0,030 0,02 0,08
68 0,035 0,02
0,10
69 0,040
0,02
0,12
Решение.
Приведенная
ниже
таблица
включает
в
себя
результаты
расчета
ве
роятностей
выбытия.
Формула
(10.5.2)
может
быть
переписана
в
виде
3
ql
T
)
= 1 -
П
(1
-
q~(j»).
j=1
в
этом
равенстве
предполагаемая
независимость
трех
причин
выбытия
очевидна.
Формула
(10.5.9)
и
условие
обязательного
выхода
на
пенсию
позволяют
получить
вероятности
выбытия
по
нескольким
причинам.
Таблица
выбытия
по нескольким
причинам
строится,
как
в
примере
10.3.1.
х
(Т)
(1)
(2)
(3)
li
r
)
d~l)
di
2
)
d~3)
qж
qж
qж
Ч;Х;
65
0,07802 0,01940 0,01940
0,03921
1000,00 19,40 19,40 39,21
66
0,10183 0,02401
0,01916 0,05867
921,99 22,14 17,67 54,09
67
0,12545
0,02851 0,01891
0,07803
828,09 23,61 15,66
64,62
68 0,14887
0,03290 0,01866
0,09731
724,20 23,83 13,51 70,47
69 0,17210 0,03720 0,01841
0,11649 616,39 22,93 11,35 71,80
70
1,00000
0,00000 0,00000 1,00000
510,31
0,00
0,00 510,31
~
Как
уже
было
отмечено,
если
одна
из
величин
р~Л,
p~T)
равна
нулю,
то
фор
мулы
(10.5.9)
и
(10.5.10)
неприменимы.
Необходимо
найти
какой-нибудь
другой
ме
тод.
Один
такой
метод,
который
позволяет
справиться
с
этой
неопределенностью
и
подходит
для
специальных
поправок,
базируется
на
предполагаемых
распределени
ях
выбытия
в
сопутствующих
таблицах
выбытия
по
единственной
причине,
а
не
на
предположениях
о
вероятностях
выбытия
по
нескольким
причинам,
как
в
разд.
10.5.

294
Гл.
10.
Модели
выбытия
по
нескольким
причинам
Сначала
рассмотрим
предположение
о
равномерности
распределения
моментов
вы
бытия
(в
каждом
годичном
возрастном
интервале)
в
сопутствующих
таблицах
вы
бытия
по
единственной
причине.
Мы
ограничимся
ситуацией
с
тремя
причинами
выбытия,
но
метод
и
формулы
легко
распространить
на
случай
т
>
З.
При
указан
ном
предположении
,и)
- 1 t
(Л
. - 1 2 3
О
/'
t
/'
1
tP
x
- -
qx,
J - , "
'=::::
'=::::
,
tp~(j)
J.L~)
(t) =
~
(-
tp~(j))
=
q~(j)
.
(10.6.1)
(10.6.2)
Отсюда
следует,
что
q~l)
=
11
'P~T}
1'~1)
(t)
dt
=
11
'P~1}
1'~1)
(t)
'P~(2)
'P~(3}
dt
=
q~(1}
[(1
-
tq~(2})(1
-
tq~(3})
dt
=
q~(I)
[1
_
~
(q~(2)
+
q~(3»)
+
~
q~(2)
q~(3)]
• (10.6.3)
Аналогичные
формулы
имеют
место
для
q~2)
и
q~3)
,
И
можно
проверить,
что
q~l)
+
q~2)
+
q~З)
=
q~(1)
+
q~(2)
+
q~(3)
_
(q~(1)q~(2)
+
q~(1)q~(3)
+
q~(2)q~(3))
+
q~(1)q~(2)q~(3)
=1 -
(1
-
q~(l))(l
-
q~(2))(1
-
q~(3))
=
qi
T
).
(10.6.4)
Пример
10.6.2.
Получим
вероятности
выбытия
для
возрастов
65-69
лет
из
данных
примера
10.6.1
в
предположении
равномерности
распределения
моментов
выбытия
в
каждом
годичном
возрастном
интервале
в
каждой
ИЗ
сопутствующих
таблиц
выбытия
по
единственной
причине.
Решение.
Это
-
применение
формулы
(10.6.3).
Х
'(1)
1(2)
'(3)
(1)
(2)
(3)
qж qж
qx
qx
qж
qж
65
0,020 0,02 0,04 0,01941 0,01941 0,03921
66 0,025 0,02 0,06 0,02401 0,01916 0,05866
67 0,030 0,02 0,08 0,02852 0,01892 0,07802
68
0,035 0,02 0,10 0,03292 0,01867 0,09727
69
0,040 0,02 0,12 0,03723 0,01843 0,11643
Эти
вероятности
близки
к
полученным
с
ПОМОЩЬЮ
формулы
(10.5.9)
вероятно-
стям
из
при
мера
10.6.1.
..
Мы
завершим
этот
раздел
другим
примером,
иллюстрирующим
использование
специального
распределения
дЛя
одной
ИЗ
причин
выбытия.
Иногда
в
силу
особенно
сти
моделируемой
ситуации
требуется
рассматривать
специальные
распределения.
Пример
10.6.3.
Рассмотрим
ситуацию
с
тремя
причинами
выбытия:
смер
тью,
потерей
трудоспособности
и
увольнением.
Предположим,
что
моменты
смерти
и
потери
трудоспособности
в
СОПУТСТВУЮЩИХ
таблицах
выбытия
по
единственной
причине
с
абсолютными
коэффициентами
q~(l)
и
q~(2)
соответственно
равномерно
распределены
в
каждом
годичном
возрастном
интервале.
Далее
предположим,
что
увольнение
происходит
лишь
в
конце
года
с
абсолютным
коэффициентом
q~(3).

10.6.
Построение
таблиц
выбытия
по
нескольким
причинам
295
(а)
Выведем
формулы
для
вероятностей
выбытия
по
этим
трем
причинам
в
возрастном
интервале
от
х
до
х
+1.
(Ь)
Модифицируем
формулы
для
вероятностей
в
предположении,
что
•
в
сопутствующей
модели
выбытия
по
единственной
причине
увольнение
про
исходит
лишь
в
середине
или
в
конце
года,
•
увольнение
происходит
в
середине
или
в
конце
года
равными
долями,
по
(1/2)q~(3)
от
числа
работавших
на
начало
рассматриваемого
года.
Замечание.
До
сих
пор
наши
модели
выбытия
по
нескольким
причинам
были
непрерывными,
за
исключением,
возможно,
установления
обязательного
возраста
выхода
на
пенсию.
Кроме
того,
мы
начали
с
модели
выбытия
по
нескольким
причи-
нам
и
после
определения
интенсивности
выбытия
Jl<j}
(t), j =
1,2,
...
,
т,
перешли
к
сопутствующим
таблицам
выбытия
по
единственной
причине.
В
этом
примере
мы
начнем
с
таблиц
выбытия
по
единственной
причине.
В
одной
ИЗ
этих
таблиц
вы
бытие происходит
дискретно,
в
конце
данного
интервала.
Мы
не
будем
пытаться
определить
интенсивность
выбытия
для
этого
дискретного
случая,
но
продолжим
построение
модели
выбытия
по
нескольким
причинам,
исходя непосредственно
из
таблиц
выбытия
по
единственной
причине
и
соотношений
(10.2.19)
и
(10.5.2),
выве
денных
нами
ранее.
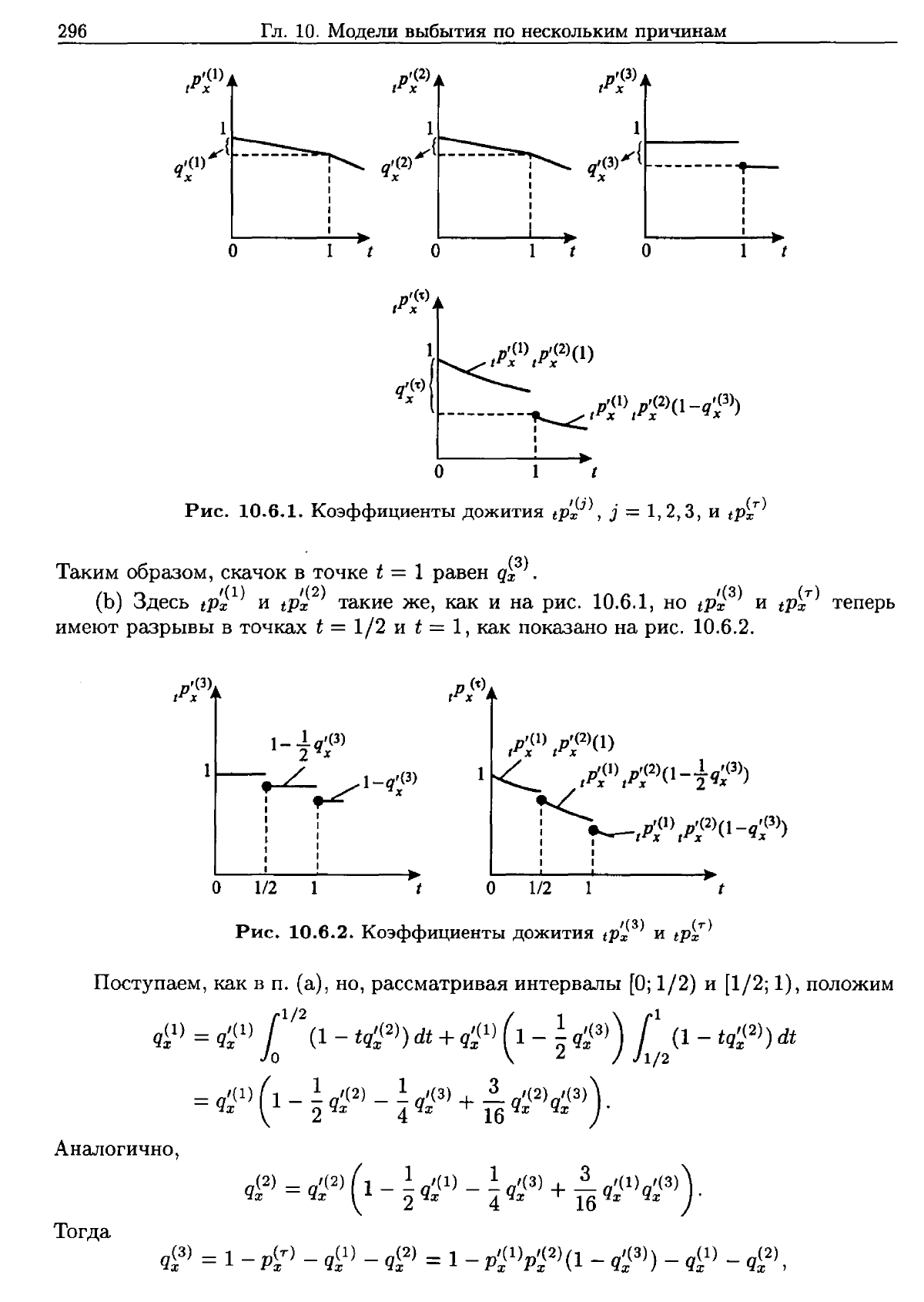
Решение.
(а)
На
рис.
10.6.1
изображены
коэффициенты
дожития
для
данных
таблиц
выбытия
по
единственной
причине
и
для
таблицы
выбытия
по
нескольким
причинам,
где
tP~T}
=
tP~l}
tP~2}
tР~З}
для
нецелых
t
~
О.
При
t =1
функции
tР~З)
И
(Т)
tPx
имеют
разрыв,
так
что
мы
рассматриваем
Нт
р(Т)
=p'(1}p'(2}1
и
р(Т)
=
p'(1)pJ(2)
(1 _
q'{З})
t-tl-
t
х
х
х
х х х
х·
Мы
также
требуем,
чтобы
для
нашей
таблицы
выбытия
по
нескольким
причинам
выполнялось
соотношение
q1
T
) =
qi
1
)
+
q~2}
+
qi
З
)
=1 _
p~T)
=1 _
p~1}p~2}
(1
_
q~(3»).
Полагаем
q~')
=[
tP~T)I'~')(t)
dt =[
tP~1)tP~2)(1)1'~')(t)
dt
=
q~(I)
[
(1
-
tq~(2))
dt
=
q~(I)
( 1 _
~
q~(2)
) .
Аналогично,
Тогда
qi
З
)
=
qi
T
)
-
(qi
1
)
+
qi
2
})
= 1 -
p~{1)p~(2}(1
_
q~(3})
_
q~(1)
_
q~(2)
+
q~(1}q~(2),
и,
поскольку
1 _
q,(l}
_
q'(2)
+
q'(1)q'{2)
=
p'(1)p'(2)
х х х
х
х
Х'
получим
q
(З)
=
р'(1)р'(2)q'(З)
х
х
х х
.
Заметим,
что
296
Гл.
10.
Модели
выбытия
по
нескольким
причинам
р'(З)
t
Х
1
q,(з),{I-_-_-
__
-_-_-
__
-...-
Х
I
I
I
I
I
I
t
1
о
t
1
р'(2)
t
Х
о
1
,..{
q'(2)
х
t1
о
о
1
t
Р
О
К
фф
'и)
. 1 2 3
(Т)
НС.
1
.6.1.
оз
ициенты
дожития
tpx
,)
= , ,
,и
tpx
Таким
образом,
скачок
в
точке
t = 1
равен
q~3)
.
( )
'(1)
1(2)
'(3)
Ь
Здесь
tPx
и
tPx
такие
же,
как
и
на
рис.
10.6.1,
но
tPx
и
имеют
разрывы
в
точках
t =
1/2
и
t = 1,
как
показано
на
рис.
10.6.2.
tP~T)
теперь
1-
~ч,(3)
2
х
11---! /
~
l-q~(3)
I
I I
I I
I I
1 I
I I
I I
о
1/2
1
t
о
1/2 1
t
Рис.
10.6.2.
Коэффициенты
дожития
tP~(3)
и
tP~T)
Поступаем,
как
в
п.
(а),
но,
рассматривая
интервалы
[О;
1/2)
и
[1/2; 1),
положим
qi
1
)
=
q~(I)
11/2
(1
-
tq~(2))
dt
+
q~(i)
(1
-
~
q~(3))
1;2
(1
-
tq~(2))
dt
=
q'(I)
(1
_!
q'(2)
_ !
q'(З)
+
~
q/(2)q/(З»)
х
2
х
4
х
16
х
х
.
Аналогично,
q
(2)
=
q'(2)
(1
_!
q/(l)
_ !
q'(3)
+
~
q'(1)q/(3))
х
х
2
х
4
х
16
х х
.
Тогда

Упражнения
297
что
приводит
К
формуле
q
(З)
=
q'(З)
(1
_
~
q'(l)
_
~
q'(2)
+
~
ql(1)ql(2))
.
х х
4
Х
4
Х
8Х
х
10.7.
Замечания
и
литература
Исторический
обзор
теории
выбытия
по
нескольким
причинам
содержится
в
работе
[Seal 1977].
В
работе
[Chiang 1968]
теория
излагается
на
языке
конкуриру
ющих
рисков.
Основы
актуарной
теории
моделей
выбытия
по
нескольким
причи
нам
были
заложены
Мейкемом
[Makeham 1874].
Работы
[Menge 1932], [Nesbitt,
Уап
Еепат
1948]
посвящены
детерминистической
интерпретации
интенсивностей
выбы
тия
и
вступления.
Бикнелл
и
Несбитт
[Bicknell, Nesbitt 1956]
развивают
очень
обrцyю
теорию
страхования
отдельного
лица,
используя
детерминистическую
модель
выбы
тия
по
нескольким
причинам.
Хикман
[Hickman 1964]
развивает
эту
же
теорию
на
языке
стохастической
модели,
и
это
изложение
составляет
основу
большей
части
на
стоящей
главы.
Анализу
таблиц
с
выбытием
по
причине
смерти
посвящены
работы
[Greville 1948], [Preston, Keyfitz, Schoen 1973].
Озадачивающие
результаты
оценивания
в
случае
зависимых
случайных
величин
обсуждались
в
работе
[Elandt-Johnson, Johnson 1980].
Промислов
[Promislow
1991Ь]
высказал
замечательную
мысль,
что
на
практике
модели
выбытия
по
нескольким
причинам
должны
быть
селекционными
в
смысле
гл.
3.
Он
развил
теорию
и
соот
ветствующие
обозначения
для
селекционной
модели
с
несколькими
причинами
вы
бытия.
Упражнения
10.3
и
10.24
основываются
на
обсуждении
из
работы
[Robinson
1984].
В
статье
[Carriere 1994]
связки,
обсуждавшиеся
в
разд.
9.6.2,
применены
для
получения
распределений
с
несколькими
причинами
выбытия,
которые
включают
зависимые
координатные
случайные
величины.
Там
же
обсуждается
проблема
иден
тификации
и
дается
обзор
условий,
при
которых
возможно
идентифицировать
един
ственную
функцию
дожития
ST1
(Х),Т2(Х)
(t,
t).
Упражнения
к
разделу
10.2
10.1.
Пусть
ILfP(t)
=JL~)(O),
j = 1,2,
...
,т,
t
~
О.
Выразите
(а)
!T,J(t,j),
(Ь)
!J(j)
,
(с)
!T(t).
Функции,
о
которых
идет
речь
в
пп.
(а)
и
(с)
-
это
совместная
«плотность~
и
марги
нальная
плотность,
а
функция
из
п.
(Ь)
-
функция
вероятностей.
Покажите,
что
Т
и
J -
независимые
случайные
величины.
10.2.
Интенсивности
выбытия
для
модели
выбытия
по
двум
причинам
заданы
форму
лами
t < 100 -
х.
(2)
_ 2
и
ILХ
(t) - 100 _
(х
+
t)'
(1)
_ 1
ILх
(t) - 100 -
(х
+t)
Найдите
формулы
при
х
= 50
для
(а)
!T,J(t,j),
(Ь)
!T(t),
(с)
!J(j),
(d)!J
I
ти
It).
10.3.
Пусть
задана
функция
«плотности»
совместного
распределения
f
(
t
')
_
{ри
1
е-(и1
+V1)t
+
(1
-
р)и2
e-(U
2
+V
2
)t,
О:::';
t, j =
1,
T,J
,)
-
-(U1+Vl)t
+
(1
)
-(U2+
V
2)t
О
./
. 2
PVl
е
-
Р
V2
е
,~
t, ) = ,
где
О
<
Р
< 1
и
О
<
иl,
и2
,
Vl
J
V2.
Найдите

298
Гл.
10.
Модели
выбытия
по
нескольким
причинам
(а)
функцию
плотности
!r(t)
и
функцию
вероятностей
!J(j),
(Ь)
функцию
дожития
sr(t).
К
разделу
10.3
10.4.
Используя
вероятности
выбытия
по
нескольким
причинам
из
примера
10.3.1,
оцените
следующие
выражения:
()
(Т)
(Ь)
(1)
()
(2)
а
ЗР65
,
Зjq65'
С
зq65'
10.5.
Следующие
вероятности
выбытия
по
нескольким
причинам
относятся
к
студен
там,
поступившим
в
колледж
с
четырехлетним
сроком
обучения.
Вероятность
Пошаговая
продол
жительность
учебы
на
начало
академи
ческого
года
выбытия
по причи
не
академической
не
успеваемости,
j = 1
выбытия
по
другим
причинам,
j = 2
выбытия
по
причи
не
успешного
окон
чания
академиче
ского
года
о
1
2
3
0,15
0,10
0,05
0,00
0,25
0,20
0,15
0,10
0,60
0,70
0,80
0,90
Количество
поступивших
1000
человек.
(а)
Найдите
математическое
ожидание
числа
окончивших.
Чему
равна
дисперсия?
(Ь)
Каково
математическое
ожидание
числа
тех,
кто
будет
исключен
за
неуспеваемость
в
течение
всей
четырехлетней
программы?
Чему
равна
дИсперсия?
10.6.
Постройте
таблицу
выбытия
по
нескольким
причинам
на
основе
данных
из
упр.
10.5
и
используйте
ее,
чтобы
найти
(а)
маргинальное
распределение
с.в.
J
(причины
выбытия),
которая
принимает
значе
ния
выбытия
по
академический
неуспеваемости,
выбытия
по
другим
причинам
и
выбытия
по
причине
успешного
окончания
колледжа,
(Ь)
условное
распределение
причины
выбытия
при
условии,
что
студент
прекращает
обучение
в
третий
год.
1,
предполагая,
что
[~T)
=
а,
'и)
(
с)
т'(Л
=
_----"q'-ж_~~
ж
1 -
(1/2)q~(Л
(Л
(Ь)
т(Л
_
qж
ж
- 1 _
(1/2)q~T)
,
к
разделу
10.4
10.7.
При
jL(l)(X)
=
l/(а-х),
О
~
х
<
а,
и
jL(2)(X)
найдите
(а)
li
T
),
(Ь)
d~l),
(с)
d~2).
10.8.
При
jL(l)(X)
=
2х/(а
-
х
2
),
О
~
Х
<
va,
jL(2)(x)
=
С,
С
>
О,
и
[~T)
= 1000
найди-
те
li
T
)
•
10.9.
Найдите
выражения
для
(
а)
d
q(T)
(Ь)
d q(j)
(с)
51:
q(j)
dx
t
ж,
dx
t
ж,
dt
t
ж
К
разделу
10.5
10.10.
Используя
данные
из
упр.
10.5
и
предполагая,
что
моменты
выбытия
в
модели
выбытия
по
нескольким
причинам
имеют
равномерное
распределение,
составьте
таблицу
значений
q~(Л,
j =
1,2,
k =
0,1,2,3,
где
k -
пошаговая
продолжительность
учебы.
10.11.
Пусть
jL~l)
(t)
равна
константе
с
при
О
~
t
~
1.
Выразите
в
терминах
с
и
tP~T)
следующие
величины:
(а)
q~(l),
(Ь)
m1
1
),
(с)
q~l).
10.12.
Покажите,
что
при
подходящих
предположениях
о
равномерности
распределе
ния
моментов
выбытия
(Т)
(а)
т(Т)
_
qж
ж
- 1 _
(1/2)q~T)
,

и,
обратно,
Упражнения
299
(Т)
тх(л
1(Л
(d)
(Т)
=
т
х
(е)
и)
=
(с)
I(Л
=
т:с
.
qx
1 _
(1/2)т~T)
,
qx
1 _
(1/2)т~T)
, qx 1 -
(1/2)т~(п
10.13.
Упорядочите
по
возрастанию
следующие
величины:
q~(j),
q~j),
т~и).
Поясните
ваши
соображения.
10.14.
Пусть
для
таблицы
выбытия
по
двум причинам
q~'ol)
= 0,02
и
q~~2)
= 0,04.
Вычислите
qi~)
с
точностью
до
четырех
знаков
после
запятой.
10.15.
Пусть
для
модели
выбытия
по
двум
причинам
тi~)
= 0,2,
q~'ol)
= 0,1.
Подсчи
тайте
q~'o2)
с
точностью
до
четырех
знаков
после
запятой,
предполагая:
(а)
равномерность
распределения
моментов
выбытия
в
этой
модели
выбытия
по
несколь
ким
причинам,
(Ь)
равномерность
распределение
моментов
выбытия
в
сопутствующих
таблицах
вы
бытия
по
единственной
причине.
10.16.
Используя
данные
из
упр.
10.5
и
предполагая
равномерность
распределения
мо
ментов
выбытия
в
модели
выбытия
по
нескольким
причинам,
постройте
таблицу
значений
т?),
j = 1, 2, k =
О,
1,
2,
3,
где
k -
пошаговая
продолжительность
учебы.
Подсчитайте
значения
с
точностью
до
пятого
знака
после
запятой.
10.17.
При
условии,
что
выбытие
может
произойти
вследствие
смерти
(1),
потери
тру
доспособности
(2)
или
выхода
на
пенсию
(3),
с
помощью
формулы
(10.5.9)
постройте
та
блицу
выбытия
по
нескольким
причинам,
основанную
на
следующих
абсолютных
коэффи
циентах:
Возраст
х
62
63
64
0,020
0,022
0,028
0,030
0,034
0,040
0,200
0,100
0,120
10.18.
Пересчитайте
таблицу
выбытия
по
нескольким
причинам
на
основе
абсолютных
коэффициентов
выбытия
из
упр.
10.17
при
помощи
nрuб.л.u::нсе'Н.uя
nовозраст'Н.'bLХ
",оэффu-
чuе'Н,тов
выбытия.
[Указание.
Для
этого
сначала
рассчитайте
т~(j)
по
формуле
'и)
I(Л
~
qx
т
х
-
(")'
j =
1,2,3,
1 -
(1/2)q~
J
которая
выполняется,
если
распределения
моментов
выбытия
в
сопутствующих
таблицах
выбытия
по
единственной
причине
равномерны.
Затем
предположите,
что
т~)
,..,.
т~(j),
j =
1,2,3,
и
получите
q~Л
по
формуле
d
(j)
d(j)
т:си)
(Л
х х
qx
=
l~T)
-
llT)
_
(1/2)d~T)
+
(1/2)d~T)
- 1 +
(1/2)т~T)
.
Это
второе
соотношение
имеет
место,
если
распределение
моментов
выбытия
по
всем
при
чинам
в
таблице
выбытия
по
всем
причинам
является
равномерным.
Но
тогда
tP~T)
=1 -
tq~T)
#
tP~(l)
tP~(2)
tP~(3)
=
(1
-
tq~(l})(l
-
tq~(2})(1
_
tq~(3»)
при
условии
равномерности
распределений
в
сопутствующих
таблицах
выбытия
по
един
ственной
причине.
Таким
образом,
имеется
некоторая
несогласованность
в
предположени
ях,
но
расчеты
могут
быть
достаточно
точными
для
первого
приближения.]
10.19.
Обоснуйте
следующие
соотношения:
1(j)
'"
(з)
q~(j)
~
q~j)
(а)
т
х
=
т
х
,
(Ь)
1 _
(1/2)q~(j)
- 1 _
(1/2)q~T)
.
Покажите,
что
тогда

300
Гл.
10.
Модели
выбытия
по
нескольким
причинам
l(j)[l
(1/2)
(Т)]
(})
()
(j)
~
qж
-
qж
(d) I
(j)
~
qж
С
qж
- 1 _
(1/2}q~(j)'
qж
- 1 _
(1/2)(q~T)
_
q~j)
.
Сравните
формулы
пп.
(с)
и
(d)
с
формулами
(10.5.9)
и
(10.5.10).
10.20.
Используйте
величины
q~/)
и
q~(j)
из
примера
10.5.1,
чтобы
вычислить
т~)
и
т~(j)
, j = 1, 2,
х
= 65,
...
,69,
при
подходящих
предположениях
о
равномерности
распре
деления
моментов
выбытия
(см.
упр.
10.12).
10.21.
Какие
из
следующих
утверждений
верны?
Исправьте
их,
если
необходимо.
и)
/.1
I(T)
()
и)!::::!
т
ж
(Ь)
I(T) dt!::::!
ж
а
qx
- 1 +
(1/2)т~)
,
о
ж+t
-
-1-+-(-I-/-2-)т---;-~T~)
,
(с)
q~l)
=
q~(l)[1
-
(1/2)q~(2)]
в
таблице
выбытия
по
двум
причинам,
если
в
каждой
из
сопутствующих
таблиц
выбытия
по единственной
причине
выбытия моменты выбытия
в
течение
года
от
возраста
х
до
возраста
х
+1
распределены
равномерно.
10.22.
(а)
Покажите,
что
для
некоторого
возраста
х,
для
отдельной
причины
выбытия
j
и
для
константы
Kj
следующие
условия
эквивалентны:
(i)
tqV)
=
К
з
tq1
T
),
О
~
t
~
1,
(ii)
p,Cj)
(t) =
Кз
p,~T)
(t),
О
~
t
~
1,
(iii) 1 -
tq~(j)
=
(1
-
tq~T»Kj,
О
~
t
~
1.
[Указание.
Покажите,
что
(i)
=>
(ii)
=>
(Ш)
=>
(ii)
=>
(i).]
(Ь)
Проверьте,
что
если
в
таблице
выбытия
по
нескольким
причинам
либо
p,~)(t)
=
JL~)(O),
О
~
t
~
1, j =
1,2,
...
,т
(интенсивность
выбытия
для
каждой
причины
выбытия
постоянна),
либо
tq~j)
=
tq~j),
О
~
t
~
1,
j =
1,2,
...
,т
(равномерное
распределение
моментов
выбытия
для
каждой
причины
выбытия),
то
tq~j)
=
Kj
tq~T),
О
~
t
~
1, j =
1,2,
...
,т.
(
с)
Предположим,
что
в
условии
(Н)
п.
(
а)
p,~T)
(t),
О
~
t
~
1,
задается
формулой
(i)
kC',
k >
О,
n >
О
(Вейбулл),
(н)
Bc
t
,
В
>
О,
с
> 1
(Гомперц).
Для
каждого
случая
найдите
соответствующие
выражения
для
tq~j)
и
1 -
tq~(j).
10.23.
(а)
Докажите,
что
p,~)(t)
=
Kj
Jl~T)(t),
О
~
t,
j =
1,2,
где
Kj
=
/.00
tP~T)
p,<j)
(t)
dt,
j =
1,
2,
тогда
и
только
тогда,
когда
С.в.
Т
и
J
независимы.
(Ь)
Покажите,
что
если
С.в.
Тl
(х)
И
Т
2
(х)
независимы,
то
tp'(j)
=
(tP~T»Kj
, j =
1,2.
[Замечание.
Обратите
внимание,
что
Kj
= fJ(j).]
10.24.
Это
упражнение
является
продолжением
упр.
10.3
и
использует
обозначения
из
разд.
10.5.5.
Совместная
функция дожития
задана
формулой
STl,T2(tl,t2)
=pe-Ultl-Vlt2
+
(l_p)e-u2tl-V2t2,
О
~
tl,t2,Ul,U2,Vl,V2,
О
<р
<
1.
Проверьте,
что
ST
1
,Т2
(t,
t)
1=
BTl
,Т2
(t, O)BTl
,Т2
(О,
t)
и
alnSTl,T2(tl,t2)
1=
_
dlnSTl,T2(t,0)
atl
tl
=t2
=t
dt'
к
разделу
10.6
10.25.
Еще
раз
проделайте
упр.
10.10
с
использованием
формулы
для
q~(j)
из
упр.
10.19.
10.26.
Покажите,
что
p,~)
(1/2) =
т~),
предполагая,
что
в
контексте
выбытия
по
нескольким
причинам
распределение
моментов
выбытия
по
каждой
причине
в
каждом
годичном
возрастном
интервале
равномерно.
