Бауэрс Н., Гербер Х., Джанс Д., Несбитт С., Хикман Дж. Актуарная математика
Подождите немного. Документ загружается.


Упражнения
271
(f)
вероятность
того,
оба
лица
умрут
в
течение
n
лет.
9.5.
Покажите,
что
вероятность
того,
что
лицо
(х)
проживет
n
лет,
а
лицо
(у)
проживет
n - 1
лет,
может
быть
выражена
как
nPx:y-l/Ру-l
или
Рх
n-lРХ+l:у.
9.6.
Вычислите
f.n
tpxx
J.Lxx
(t) dt.
9.7.
Используя
распределения
С.в.
Т(х)
и
Т(у)
из
упр.
9.1,
найдите:
(а)
функцию
распределения
С.В.
Т(ху),
(Ь)
функцию
дожития
с.в.
Т(ху)
и
(с)
Е[Т(ху)].
Предположите,
что
n>
3.
9.8.
Используйте
формулу
(9.3.8),
чтобы
получить
функцию
плотности
с.в.
Т(ху),
исходя из
совместного
распределения
с.в.
Т(х)
и
Т(у),
заданного
в
примере
9.2.3.
К
разделу
9.4
9.9.
Покажите
алгебраическими
выкладками
и
из
общих
соображений,
что
tPFg
=tPxy +
tPx(1-
tPx) +tPll(l - tPx).
9.10.
Найдите
вероятность
того,
что по
крайней
мере
одно
из
двух
лиц
(х)
и
(у)
умрет
в
(n +
l)-м
году.
Равна
ли
она
величине
nlqxy?
Приведите
объяснения.
9.11.
Функция
плотности
совместного
распределения
с.в.
Т(х)
и Т(у)
задана
в
упр.
9.1.
Найдите
(а)
функцию
распределения
и
функцию
плотности
С.в.
Т(ху),
(Ь)
Е[Т(ху)]
для
n>
3,
(с)
J.Lxy(t).
К
разделу
9.5
9.12.
Пусть
25Р25:50
= 0,2
и
lsP25
= 0,9.
Рассчитайте
вероятность
того,
что
лицо
(40)
доживет
до
возраста
75
лет.
9.13.
Пусть
J.L
=
1/(100
-
х)
для
О
~
х
< 100.
Рассчитайте
(а)
10Р40:50,
(Ь)
10Р40:50'
(с)
~40:50,
(d)
~40:S0'
(е)
D[T(40:50)], (!) D(T(40:50)],
(g) Cov[T(40:50),
Т(40:50)),
(h)
коэффициент
корреляции
между
Т(40:50)
и
Т(40:50).
9.14.
Вычислите
d~xx/dx.
9.15.
Покажите,
что
вероятность
того,
что
два
лица
(30)
и
(40)
умрут
в
одном
и
том
же
году,
может
быть
записана
следующим
образом:
1 +
еЗО:40
-
рзо(l
+
еЗl:40)
-
Р40(1
+
еЗО:41)
+
Р30:40(1
+
еЗl:41).
9.16.
Покажите,
что
вероятность
того,
что
два
лица
(30)
и
(40)
умрут
в
одном
и
том
же
возрасте,
может
быть
выражена
в
виде
'lорзо(l
+
е40:40)
- 2
llрзо(l
+
e4o:41)
+
Р40
llрзо(l
+
е41:41).
9.17.
Предположим,
что
интенсивности
смертности
для
лиц
1
и
П
составляют
соответ
ственно
J.L
I (
х)
=ln(1
0/9)
для
всех
х,
J.L
11
(х)
=
(1
О
-
х)
- 1
для
О
~
х
< 1
О.
Вычислите
вероятность
того,
что первая
смерть
произойдет
в
точности
между
возрастами
3
и
5
лет
при
условии,
что
возраст
обоих
лиц
~
в
точности
1
год.
к
разделу
9.
б
9.18.
Это
продолжение
примера
9.6.3.
Выразите
(а)
функцию
распределения
С.в.
Т(ху),
(Ь)
функцию
плотности
С.в.
Т(ху).
9.19.
Вычислите
значение
функции
F
T
(x)T(y)(5,
5),
используя
(9.6.7),
если
sqx
= 0,05
и
sqy
=0,03.
Ответ
зависит
от
значения
параметра
а.
9.20.
Используйте
результат
упр.
9.19,
чтобы
вычислить
sl]Жy
при
(а)
Q =
О,
(Ь)
а
=3
и
(с)
Q'
=
~3.
[Указание.
Используйте
соотношения
(9.4.5)
и
(9.3.2).]

272
Гл.
9.
Актуарные
функции
для
нескольких
лиц
к
разделу
9. 7
9.21.
Покажите,
что
a'xY':1il
=
аm
+
nlaxy.
Опишите
соответствующие
выплаты.
9.22.
Опишите
актуарную
настоящую
стоимость,
обозначаемую
через
A
x
:
1il
.
Покажите)
что
A
x
:
1il
=
Ах
- A
X
:
1il
+v
n
.
,
9.23.
Покажите,
что
cov(vT(X:l/)
,
vT(x
y
»)
=
(Ах
-
Аху)(А
у
-
Аху)
для
независимых
продолжительностей
предстоящей
жизни
Т(х)
и
Т(у).
9.24.
Выразите
актуарную
настоящую
стоимость
непрерывного
аннуитета
с
выплатой
размера
1
в
год
до
тех
пор,
пока
по
крайней
мере одно
из
двух
лиц
(25)
и
(30)
живо
и
не
достигло
50-летнего
возраста,
в
терминах
аннуитетов,
связанных
с
дожитием
отдельного
лица
и
всех
лиц
из
группы.
9.25.
Выразите
актуарную
настоящую
стоимость
отсроченного
аннуитета
с
выплатой
размера
1
в
конце
каждого
года,
когда
живо
хотя
бы
ОдНО
из
лиц
(25),
(ЗО),
при
условии,
что
оно
достигло
возраста
50
лет,
в
терминах
аннуитетов,
связанных
с
дожитием
отдельного
лица
или
всех
лиц
из
группы.
9.26.
Выразите
актуарную
настоящую
стоимость
аннуитета
пренумерандо
на
срок
n
лет
для
статуса
(ху),
обеспечивающего
ежеГОдНые
выплаты
размера
1
до
тех
пор,
пока
оба
лица
живы,
сокращающиеся
до
1/2
в
случае
смерти
лица
(х)
или
до
l/З
в
случае
смерти
лица
(у),
в
терминах
аннуитетов,
сопряженных
со
статусами
дожития
одного
лица
и
обоих
лиц.
9.27.
Аннуитет
постнумерандо
обеспечивает
выплату
размера
1
лицу
(х)
до
тех
пор,
пока
живо
оно
и
лицо
(у),
а
также
в
течение
n
лет
после
смерти
последнего,
причем
в
любых
обстоятельствах
через
m
лет,
т
>
n,
считая
с
настоящего
момента,
выплаты
прекращаются.
Покажите,
что
его
актуарная
настоящая
стоимость
составит
ax:1il
+
nЕ
х
аж+n:у:m-nl'
9.28.
Выразите
актуарную
настоящую
стоимость
непрерывного
аннуитета
с
выплатой
размера
1
в
год
когда
по
крайней
мере одно
из
лиц
(40)
и
(55)
живо
и
достигло
60
лет,
за
исключением
периода,
когда
лицо
(40)
живо,
но
не
достигло
55
лет.
9.29.
Аннуитет
в
пользу
двух
лиц
(х)
и
(у)
выплачивается
с
некоторой
начальной
интенсивностью
до
тех
пор,
пока
лицо
(х)
живо,
а
если
лицо
(у)
переживает
лицо
(х),
то
выплаты
продолжаются
с
интенсивностью,
составляющей
часть
р,
1/2
~
Р
~
1,
от
начальной
интенсивности.
(а)
Выразите
актуарную
настоящую
стоимость
такого
аннуитета
пренумерандо
с
на
чальной
интенсивностью
1
в
год
и
с
выплатами
m
раз
в
год
в
терминах
актуарных
насто
ящих
стоимостей
аннуитетов,
сопряженных
с
дожитием
одного
лица
и
обоих
лиц.
(Ь)
Говорят,
что
бессрочный
аннуитет
в
пользу
двух
лиц
(х)
и
(у)
и
страховой
аннуитет
для
лица
(х)
актуарно
эквивалентны
на
основе
сформулированных
предположений,
если
при
этих
предположениях
они
имеют
равные
актуарные настоящие
стоимости.
Выразите
отношение
начальной
интенсивности
выплат
пожизненного
аннуитета
в
пользу
двух
лиц
к
интенсивности
выплат
актуарно
эквивалентного
аннуитета
для
одного
лица
(х).
9.30~2Пока~~те,
~TO
д
_
--2
(а)
Аху
=
Аху
-
baYl
x
'
(Ь)
дх
аУl
ж
=
р(х)
ayJx
-
Аху·
[Указание.
Пункт
(а)
опирается
на
материал
разд.
9.9.]
К
разделу
9.8
9.31.
Покажите,
что
если
в
случае
закона
Мейкема
статус
(ху)
заменяется
на
статус
(шш),то
ln(c.:l+1)-ln2
w -
у
=
lпс
'
где
Д
=
х
-
у
~
О.
(Это
показывает,
что
w
можно
получить
из
более
молодого
возрас
та у
прибавлением
величины,
являющейся
функцией
разности
Д =
х
-
у.
Это
свойство
называют
зах;оном
равномерного
старшuнства.
9.32.
С
помощью
вашей
Иллюстративной
таблицы
смертности
и
процентной
ставки
б%
рассчитайте
a
50
:
60
:ТQ1'
Для
решения
используйте

Упражнения
273
то
(а)
величины,
полученные
интерполяцией
значений
таблицы
для
U:z:ж,
(Ь)
величины,
заимствованные
из
таблицы
для
Ux:x+10.
9.33.
Покажите,
что
для
таблицы
смертности,
соответствующей
закону
Мейкема,
и
таких
возрастов
х
и
у
лет,
что
статус
(ww)
является
эквивалентным
им
статусом
с
одина
ковыми
возрастами,
(а)
tpw
является
средНИМ
геометрическим
величин
tРж
и
tPy,
(Ь)
tРж
+tPy > 2tPw,
если х
f:.
у,
(с)
ажу
> a
ww
,
если
х
f:.
у.
9.34.
Покажите,
что
для
таблицы
смертности,
соответствующей
закону
Мейкема,
ве
личина
а;су
равна
актуарной
настоящей
стоимости
аннуитета
для
одного
лица
(ш),
где
C
w
=
еЖ
+
су
и
интенсивность
начисления
процента
(/
равна
0+
А.
Затем
покажите, что
А
жу
=
A~
+
Aa~,
где
величины
со
штрихом
вычислены
при
интенсивности
начисления
процента
6'.
9.35.
Рассмотрим
две
таблицы
смертности,
одну
-
для
мужчин
(М),
другую
-
для
женщин
(F),
причем
J.LM(z)
=
3a+3bz/2
и
J.LF(Z)
=
a+bz.
Мы
хотим
использовать
таблицу
актуарных
настоящих
стоимостей
для
двух
лиц
возраста
w
каждое,
мужчины
и
женщины,
для
вычисления
актуарной
настоящей
стоимости
аннуитета,
сопряженного
со
статусом
до
ЖИТИЯ
двух
лиц:
мужчины
возраста
х
лет
и
женщины
возраста
у
лет.
Выразите
w
через
х
и
у.
9.36.
Из
разд.
9.5
известно,
что
если
С.В.
Т(х)
и
Т(у)
независимы,
то
имеет
место
равенство
а;су
=
/.00
е
-
JJ
[О+I"(Ж+8)+~(У+8)]ds
dt.
Если
найдутся
такие
о',
k
и
Ш,
что
0+
J.L(x
+t) +
J.L(Y
+
t)
=
о'
+
kJ.&(
W +
t),
а
ху
=
/.00
vt(tPw)k
dt
=
ii~(k)'
Здесь
штрих
означает,
что
при
вычислении
используется
интенсивность
начисления
про
цента
6',
а
w(k)
указывает
на
статус
дожития
группы
k
«лиц»
(k
не
обязательно
целое).
Покажите,
что
если
J.&(x
+t) =
а
+
Ь(х
+t) +
с(х
+t)2,
то
(*)
выполняется
при
k =2,
w =
(х
+
у)/2,
о'
=
0+
с(х
2
+
у2
- 2w
2
).
о
9.37.
Найдите
ез.:у,
если
qж
=
qy
= 1
и
моменты
смерти
равномерно
распределены
в
течение
годичного
возрастного
интервала
для
каждого
из
двух
лиц
(х)
и
(у).
9.38.
Пусть
с.в.
Т(х)
и
Т(у)
независимы и
равномерно
распределены
в
следующем
годичном
возрастном
интервале.
При
условии,
что
оба
лица
(х)
и
(у)
умрут
в
следую
щем
годичном
интервале,
покажите,
что
момент
потери
статуса
(ху)
не
является
равно
мерно
распределенным
в
течение
года.
[Указание.
Покажите,
что
Р[Т(ху)
~
t I
(Т(х)
~
1) n
(Т(у)
~
1)] =
2t
- t
2
.]
9.39.
Покажите,
что
1 1 1 ( i i
2
i
3
19i
4
)
О
i
[1
- (i/2 - i
2
/3
+i
3
/4
- i
4
/5 + ...
)]
= i 1 + 2 - 12 + 24 - 720
+...
,
а
значит,
что
i ( 2
2).
i i
3
~
1 -
~
+ i
~
6- 360 +
....
9.40.
Покажите,
что
если
моменты
смерти
равномерно
распределены
в
каждом
годич
ном
возрастном
интервале,
то
1
т
+
1-
2j
(j-l)/mРху
-
j/mPxy
= -
qxy
+ 2
qx qy
m m
для
любых
х
и
у,
j =
1,2,3,
...
,
т,
а
тем
самым
проверьте
формулу
(9.8.14).
к
разделу
9.9

274
Гл.
9.
Актуарные
функции
для
нескольких
лиц
Р[Т(х)
=
Т(у»)
=
lOO
fт(ж)т(у)
(t, t) dt.
9.41.
Из
общих
соображений
убедитесь,
что
nQ;lI =
nQx~
+
nqx
пру.
Какой
вид примет
это
равенство
при
n -+
оо?
9.42.
Покажите,
что актуарная
настоящая
стоимость
страховых
выплат
размера
1
в
конце
года
смерти
лица
(х)
при
условии,
что
лицо
(у)
доживет
до
времени
выплаты,
можно
выразить
в
виде
vp
y
a
x
:
y
+l
-
аху.
9.43.
Покажите,
что
А;lI
-
Ax~
=
Аху
-
Ау.
9.44.
В
терминах
актуарных настоящих
стоимостей
выплат
по
договорам
страхования
на
случай
смерти
отдельного
лица
и
на
случай первой
смерти
в
группе
выразите
единовре
менную
нетто-премию
для
выплаты
размера
1,
осуществляемой
в
момент
смерти
лица
(50)
при
условии,
что
лицо
(20)
(в
этот
момент
времени)
уже
умерло
или
достигло
возраста
40
лет.
9.45.
В
терминах
актуарной
настоящей
стоимости
страхования
на
дожитие
и
на
случай
первой
смерти
в
группе
выразите
актуарную
настоящую
стоимость
страхования
с
выпла
тами
размера
1,
производимыми
в
момент
смерти
лица
(х)
после
смерти
лица
(у)
при
условии,
что
(у)
умрет
в
течение
n-летнего
интервала
до
момента
смерти
лица
(х).
9.46.
Вычислите
25Q25}O,
если
/-L(x)
=
1/(100
-
х)
для
О
~
х
< 100.
К
разделу
9.10
9.41.
Известно,
что
в
таблице
смертности,
соответствующей
закону
Мейкема,
А
=
0,003
и
с
1О
= 3.
1
о
- 1
-_
(а)
вычислите
ooQ40:50,
если
е40:50
= 17,
(Ь)
выразите
А
40
:
50
В
терминах
А
40
:
50
И
а40:50.
9.48.
При
условии,
что
смертность
описывается
законом
Гомперца
с
/-L(X)
=
10-
4
2
х
/
8
- 1
-1
u
для
Х
>
35
и,что,
согласно
(9.10.12),
A40:48:IOl
=fA
w
:
IOl
'
рассчитаите
f
и
w.
К
разлu'Ч'Ным.
тем.ам.
глав'ы
9.49.
Статус
дожития
(rn)
сохраняется
ровно
n
лет.
Он
использовался
вместе
со
ста-
-
-1
- 1
тусами
дожития
лиц,
например,
в
функциях
А
х
:
m
,
А
ж
:
m
,
А
ж
:
m
,
а
ж
:
m
,
A
xy
:
7il
'
Упростите
след.ующие
выражения
и
дайте
их
словесную
интерпретацию:
- - 2
(а)
а
ж
:
7il
,
(Ь)
A
x
:
iil
'
9.50.
Докажите
соотношение
(9.4.6),
применяя
равенство
Р(А
U
В)
=
Р(А)
+
Р(В)
-
Р(А
n
В).
д
о
9.51.
Вычислите
величину дх
ежу.
9.52.
Случайные
величины
Т·(х),
Т·(у)
и
Z
независимы
и
имеют
показательное
рас
пределение
с
параметрами
/-Ll
,
J..t2,
И
Л
соответственно.
Эти
три случайные
величины
входят
в
модель
с
возмущением.
(а)
Найдите
маргинальную
функцию
плотности
С.в.
Т(у),
вычислив
fT(y)
(t)
= l'
fт(ж)Т(у)
(8,
t)
d8 +
fт(ж)т(у)
(t,
t)
+
/.00
fт(ж)т(у)
(8,
t)
d8.
(Ь)
Найдите
маргинальную
функцию
дожития
С.в.
Т(у),
вычислив
ST(y)(t) =
/.00
fT(y)(u)du.
Сравните
полученный
результат
с
соотношением
(9.6.4Ь).
(
с)
Вычислите

10
МОДЕЛИ
ВЫБЫТИЯ
ПО
НЕСКОЛЬКИМ
ПРИЧИНАМ
10.1.
Введение
В
гл.
9
мы
распространили
теорию
страхования
отдельного
лица,
рассматри
вавшуюся
в
гл.
3-8,
на
страхование
нескольких
лиц,
составляющих
совокупность
с
единственной
причиной
выбытия
-
смертью.
Теперь
мы
возвратимся
к
случаю
от
дельного
лица,
но
причин
выбытия
может
быть
несколько.
В
качестве
практического
приложения
отметим,
что
число
работников
одного
работодателя
сокращается,
ко
гда
они
увольняются,
заболевают,
умирают
или
выходят
на
пенсию.
При
анализе
рынка
рабочей
силы
иногда
необходимо
оценить
лишь
количество
тех
работающих
в
настоящее
время,
кто
останется
трудоспособным
еще
в
течении
некоторого
пери
ода
в
будущем.
Для
этой
задачи
подходит
модель
дожития,
развитая
в
гл.
3,
если
интерпретировать
основную
случайную
величину
не
как
продолжительность
пред
стоящей
жизни,
а
как
продолжительность
периода
трудовой
деятельности.
Однако
пенсионные
схемы
для
работающих
предусматривают
выплаты
при
прекращении
ими
работы,
которые
могут
зависеть от
причины
прекращения.
Например,
выпла
ты
при
выходе
на
пенсию
часто
отличаются
от
выплат
в
случае
смерти
или утраты
трудоспособности.
Следовательно,
модели
дожития
дЛя
пенсионных
схем
для
рабо
тающих включают
в
себя
случайные
величины
и
для
продолжительности
периода
до
прекращения
трудовой
деятельности,
и
для
причины
прекращения.
Структура
выплат
также
часто
зависит
от
размера
заработной
платы,
являющейся
неопреде
ленностью
совсем
другого
рода,
которую
мы
будем
обсуждать
в
гл.
11.
Другое
практическое
приложение
связано
с
тем,
что
большинство
индивидуаль
ных
договоров
страхования
жизни
гарантирует
некоторые
выплаты,
если
выплата
премий
прекращается
до
окончания
установленного
периода
их
выплаты.
Комби
нированная
модель
для
такого
страхования
рассматривает
в
качестве
случайных
величин
продолжительность
периода
до
момента
прекращения
выплаты
премий
и
причины
этого
прекращения.
Страхование
потери
дохода страхователями
вследствие
утраты
ими
трудоспо
собности
обеспечивает
периодические
выплаты
страхователям,
состояние
которых
удовлетворяет
определению
нетрудоспособности,
содержащемуся
в
договоре
страхо
вания.
В
некоторых
случаях
сумма
периодических
выплат
может
зависеть
от
того,
чем
вызвана
нетрудоспособность:
болезнью
или
несчастным
случаем.
Лицо
может
выбыть
из
совокупности
работающих
застрахованных
вследствие
смерти,
увольне
ния,
утраты
трудоспособности
и
окончания
периода
действия
договора
страхования.
Полная
модель
страхования
на
случай
утраты
трудоспособности
включает
в
себя
как
случайную
величину
продолжительности
периода
до
момента
выбытия,
когда

276
Гл.
10.
Модели
выбытия
по
нескольким
причинам
страхователь
перестает
быть
членом
совокупности
работающих,
так
и
случайную
величину
причины
выбытия.
Органы
управления
общественным
здравоохранением
нуждаются
в
анализе
смертности
и
дожития
в
терминах
причин
смерти.
Цели
общественного
здраво
охранения
могут
быть
сформулированы,
если
исследовать
совместное
распределе
ние
продолжительности
предстоящей
жизни
и
причин
смерти.
На
этом
типе
анализа
основывалось
заключение,
что
среди
причин
смерти
на
первом
месте
стоят
заболе
вания
сердечно-сосудистой
системы
и
онкологические
заболевания.
Главная
цель
этой
главы
-
построить
теорию
для
изучения
распределения
сле
дующих
двух
случайных
величин
для
отдельного
лица:
продолжительности
периода
до
момента
потери
данного
статуса
и
причины
его
потери.
Полученная
модель
ис
пользуется
в
каждом
из
приложений,
описанных
в
этом
разделе.
В
актуарной
науке
потеря
статуса
называется
въtб'Ытuе-м,
а
предмет
этой
главы
-
теорией
в'Ыб'Ытия
по
несtl:о.ль?Сu,м
npu'ttuHaM.
В
биологической
статистике
ее
называют
теорией
?CoHtl:y-
РUРУЮЩUХ
PUCtl:oe.
Теорию
выбытия
по
нескольким
причинам
возможно
также
развивать
в
терми
нах
детерминированных
коэффициентов.
Краткое
резюме
рассматриваемой
теории
с
этой
точки
зрения
будет
дано
в
разд.
10.4.
10.2.
Две
случайные
величины
Глава
3
частично
посвящена
методам
определения
и
использования
распределе
ния
непрерывной
случайной
величины
Т
(х)
продолжительности
предстоящей
жиз
ни
лица
(х).
При
небольшом
изменении
терминологии
те
же
методы
можно
исполь
зовать
для
изучения
длительности
периода
времени
до
потери
некоторого
статуса,
такого,
например,
как работа
на
определенного
работодателя.
Фактически
мы
бу
дем
пользоваться
тем
же
самым
обозначением
Т(х),
или
просто
Т,
дЛЯ
случайной
величины
длительности
временного
интервала
в
этом
новом
значении.
В
этом
разделе
мы
усложним
основную
модель,
введя
вторую
случайную
вели
чину
-
причину
выбытия,
которую
обозначим
через
J(x) =
J.
Мы
будем
предпола
гать,
что
J -
дискретная
случайная
величина.
Приложения
из
разд.
10.1
дают примеры
этих
случайных
величин.
В
приложени
ях
к
пенсионной
схеме
для
работающих
случайная
величина
J
принимает
значения
1, 2, 3
или
4
в
зависимости
от
того,
происходит
выбытие
вследствие увольнения,
потери
трудоспособности,
смерти
или
выхода
на
пенсию
соответственно.
В
приложе
нии
к
страхованию
жизни
С.в.
J
может
принимать
значения
1
или
2
в
зависимости
от
того,
происходит
выбытие
вследствие
смерти
страхователя
или
вследствие
пре
кращения
выплаты
им
премиЙ.
Для
приложения
к
страхованию
на
случай
потери
трудоспособности
С.в.
J
может
принимать
значения
1, 2, 3
или
4
в
зависимости
от
того,
умер
страхователь,
уволен,
потерял
трудоспособность
или
у
него
окончился
период
страхования.
Наконец,
в
приложениях
к
общественному
здравоохранению
существует
много
возможностей
для
задания
причин
выбытия.
Например,
в
неко
тором
исследовании
С.в.
J
может
принимать
значения
1, 2, 3
или
4
в
зависимости
от
того,
произошла
смерть
вследствие
сердечно-сосудистого
заболевания,
онкологи
ческого
заболевания,
несчастного
случая
или
всех
других
причин.
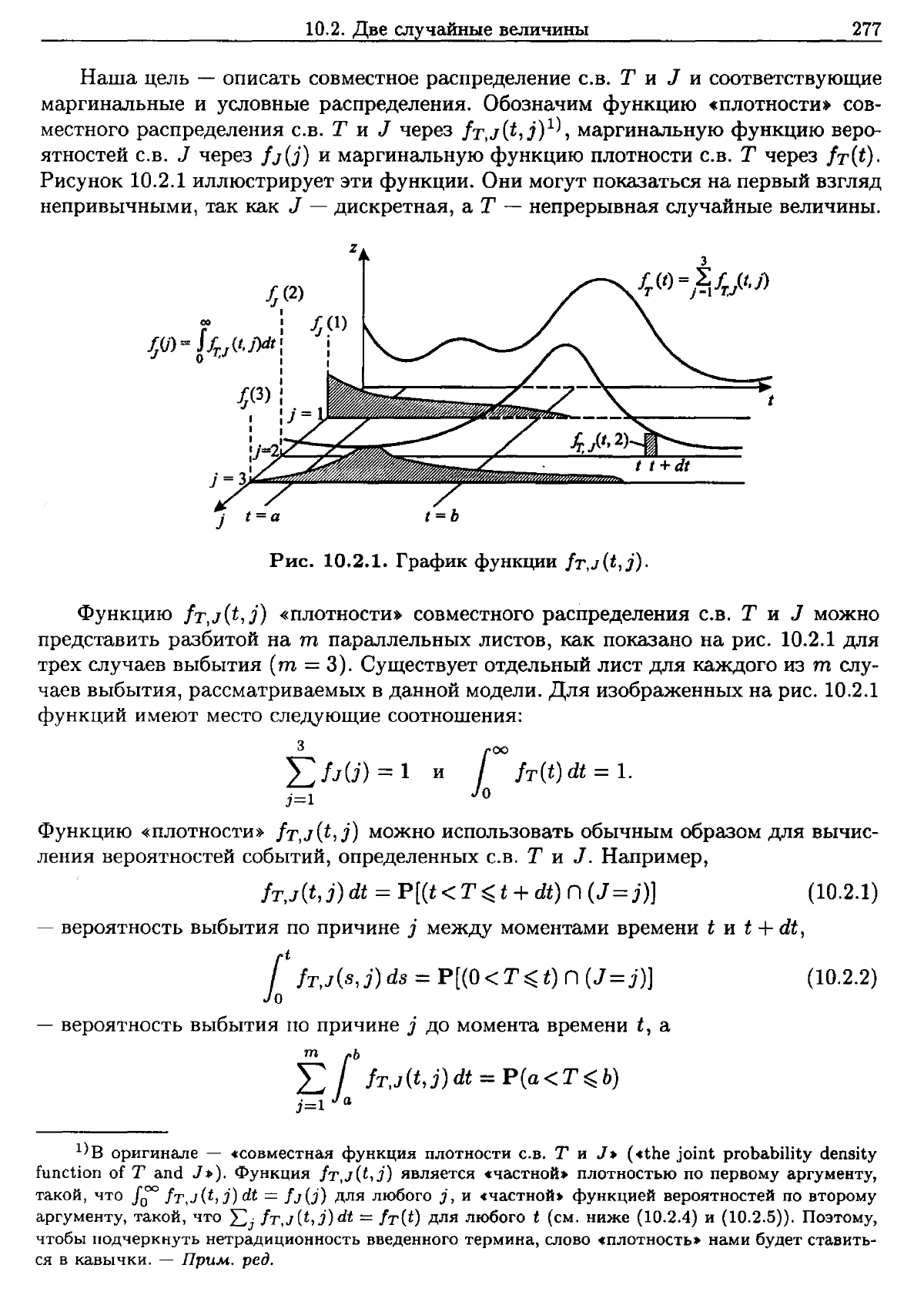
10.2.
Две
случайные
величины
277
Наша
цель
-
описать
совместное
распределение
С.В.
Т
и
J
и
соответствующие
маргинальные
и
условные
распределения.
Обозначим
функцию
«плотности.
сов
местного
распределения
с.в.
Т
и
J
через
fT,J(t,
з)1),
маргинальную
функцию
веро
ятностей
С.в.
J
через
fJ(j)
и
маргинальную
функцию
плотности
С.в.
Т
через
fT(t).
Рисунок
10.2.1
иллюстрирует
эти
функции.
Они
могут
показаться
на
первый
взгляд
непривычными,
так
как
J -
дискретная,
а
Т -
непрерывная
случайные
величины.
~(З)
00
f.
и)'"
f
Iт.;
(t,
j)dt
'J
О'
j
-&
(2)
~
~1)
I
I
I
z
Jr.)t, 2)
3
1;
(t) =
j~
Iт)t.
j)
t
t t
+dt
Рис.
10.2.1.
График
функции
!T,J(t,j).
Функцию
fT,J(t,
j)
«плотности.
совместного
распределения
с.в.
Т
И
J
можно
представить
разбитой
на
т
параллельных
листов,
как
показано
на
рис.
10.2.1
для
трех
случаев
выбытия
(т
= 3).
Существует
отдельный
лист
для
каждого
из
т
слу
чаев
выбытия,
рассматриваемых
в
данной
модели.
Для
изображенных
на
рис.
10.2.1
функций
имеют
место
следующие
соотношения:
3
~
fJ(j)
=1
и
{О
fT(t) dt =
1.
Функцию
«плотности.
fT,J(t,j)
можно
использовать
обычным
образом
для
вычис
ления
вероятностей
событий,
определенных
С.в.
Т
и
J.
Например,
fT,J(t,
j)
dt =
P[(t
<
Т
~
t +dt) n(] =
з»)
(10.2.1)
-
вероятность
выбытия
по
причине
j
между
моментами
времени
t
и
t + dt,
[
fT,J(S,j)ds
=
P[(O<T~t)
n
(J=j)]
(10.2.2)
-
вероятность
выбытия
по
причине
j
до
момента
времени
t,
а
m
{Ь
L}(1
fT,J(t,j)
dt =
Р(а
<
Т
~
Ь)
j=l
а
l)в
оригинале
-
4:совместная
функция
плотности
с.в.
Т
И
J
..
(4:the
joint
probability
density
function
of
Т
and
J
..
).
Функция
fr,J
(t,
j)
является
4:частноЙ
..
плотностью
по
первому
аргументу,
такой,
что
f
o
OO
fr,J(t,
j)
dt =
!J(j)
для
любого
j,
и
4:частноЙ.
функцией
вероятностей
по
второму
аргументу,
такой,
что
Lj
fr,J(t,j)dt
=
!r(t)
для
любого
t
(см.
ниже
(10.2.4)
и
(10.2.5)).
Поэтому,
чтобы
подчеркнуть
нетрадиционность
введенного
термина,
слово
4:ПЛОТНОСТЬ"
нами
будет
ставить
ся
в
кавычки.
-
Прим.
ред.

278
Гл.
10.
Модели
выбытия
по
нескольким
причинам
(10.2.3)
t
~
О,
j =
1,2,
...
,
т,
-
вероятность
выбытия
по
всем
причинам
между
моментами
времени
а
и
Ь.
Вероятность
выбытия
до
момента
времени
t
по
причине
j,
заданная
равенством
(10.2.2),
имеет
специальное
обозначение
tq~)
=
{!T,J(S,j)
ds,
которое
иллюстрирует
использование
верхнего
индекса
для
обозначения
причины
выбытия
в
теории
выбытия
по
нескольким
причинам.
Информация,
известная
в
возрасте
х
лет,
используется
для
выбора
распреде
ления
так
же,
как
это
делалось
в
гл.
З.
Если
известно
только,
что
лицо
возраста
х
живо,
то
следует
пользоваться
агрегативным
распределением.
С
другой
стороны,
если
имеется
дополнительная
информация,
то
следует
использовать
селекционное
распределение,
и
возраст
на
момент
селекции
будет
заключен
в
квадратные
скобки.
Согласно
определению
маргинальной
функции
вероятностей
с:в.
J,
изображен
ной
на
рис.
10.2.1
в
плоскости
и,
z)
и
обозначенной
fJ(j),
вероятность
выбытия
по
причине
j
в
произвольный
момент
времени
в
будущем
равна
(10.2.4)
j =
1,2,
...
,т.
!J(j)
=
["
!T,J(s,j)
ds =
ooq~),
Это
-
новое
обозначение,
не
имеющее
аналога
в
гл.
3,
в
отличие
от
маргинальной
функции
плотности
fT(t)
С.в.
Т,
изображенной
в
плоскости
(t,
z)
на
рис.
10.2.1.
Для
fT(t)
и
функции
распределения
FT(t)
имеем
при
t
;;:=
О
m
fT(t) =
~
fT,J(t,j),
j=l
FT(t) =
{!Т(В)
ds.
(10.2.5)
(10.2.9)
(10.2.7)
(10.2.8)
(10.2.6)
Обозначения,
введенные
в
гл.
3,
для
функций
распределения
случайной
величины
продолжительности
предстоящей
жизни
можно
распространить
на
случайную
вели
чину
продолжительности
периода
до
потери
статуса
в
м.одели
выбытия
по
несколь
ким
причинам
.
Используя
верхний
индекс
(Т)
дЛЯ
обозначения
того,
что
функция
относится
ко
всем
причинам
или
общей
интенсивности
выбытия,
получим
tq~T)
=
Р(Т:(;
t) = FT(t) = {
!Т(В)
ш,
tP~T)
=
Р(Т
>t) = 1 -
tq~T),
(Т)
_ fT(t)
__
1_.!!.-
(Т)
1_:!:.-
(Т)
__
!!.-
(Т)
J1-x
(t) - 1 _ F (t) -
(Т)
dt
tqx
-
(Т)
dt
tP
x
-
dt ln
tP
x
,
т
tPx
tPx
tP~T)
=
ехр
[
-1
t
/l;'T)
(В)
dS]
.
Математически
эти
функции
для
С.в.
Т
из
настоящей
главы
совпадают
с
соответ
ствующими
функциям
для
С.в.
Т
ИЗ
гл.
3;
различие
состоит
в
их
интерпретации
в
приложениях.
Выбор
символа
p,~T)
(t)
для
интенсивности
выбытия
по
всем
причинам
обусловлен
этими
приложениями.
Например,
в
пенеионных
приложениях
х
-
воз
раст
вступления
в
пенеионную
схему,
и
хотя
никакой
дополнительной
информации
для
селекции
может
не
быть,
причины
последующего
выбытия
могут
зависеть
от
этого
возраста.

10.2.
Две
случайные
величины
279
Как
и
в
приложениях
из
предыдущих
глав,
вероятность
(10.2.1)
можно
анали
зировать
при
условии
сохранения
данного
статуса
до
момента
времени
t.
Тогда
fr,
J(t,
j)
dt =
Р
(Т
>t)
Р
([
(t <
Т
~
t +dt) n
(J
=
j)
JI
т
>t) .
(10.2.10)
По
аналогии
с
формулой
(3.2.12)
это
подсказывает
следующее
определение
интен
сивности
вЪtбытuя
по
nрu'Чuне
j:
Jl~)(t)
= fTAt,()) = fT,Jit;j) (10.2.11)
1 -
Fr
t
tРж
Т
Интенсивность
выбытия
по
причине
j
в
возрасте
х
+t
имеет
интерпретацию
в
терми
нах
условных
вероятностей.
Это
значение
«плотности»
совместного
распределения
С.в.
Т
и
J
в
точках
х
+ t
и
j
при
условии
дожития
до
возраста
х
+ t
лет.
Тогда
формула
(10.2.10)
может
быть
переписана
в
виде
fr,J(t,j)
dt =
tp~T)J.l~)(t)dt,
j =
1,2,
...
,т,
t
~
О.
(10.2.10')
Иначе
говоря:
(вероятность
выбытия
по
причине
j
между
моментами
времени
t
и
t +dt)
=
вероятность
tP~T)
того,
что
лицо
(х)
сохранит
данный
статус
до
момента
времени
t)
х
(условная
вероятность
J.l!!)
(t)
того,
что
выбытие
произойдет
по
причине
j
между
моментами
времени
t
и
t + dt,
при
условии,
что
выбытие
не
произойдет
раньше
времени
t).
Отсюда,
дифференцируя
формулу
(10.2.3)
и
используя
формулу
(10.2.11),
ПОЛУЧflМ
J.l~j)
(t) =
~T)
~
tq~j).
(10.2.12)
tPx
Далее,
согласно
(10.2.6), (10.2.5)
и
(10.2.3),
[t
[t
m m [t m
tq~T)
=
Jn
fr(s)
ds =
Jn
L
fr,J(s,j)
ds = L
J(}
fr,J(s,j)
ds = L
tq~j).
(10.2.13)
о о
j=1 j=1
О
j=1
Тот
факт,
что
первый
и
последний
члены
в
(10.2.13)
равны,
допускает
очевидную
интерпретацию.
Комбинируя
формулы
(10.2.8), (10.2.13)
и
(10.2.12),
получаем
т
J.l~T)
(t) = L
р~Л
(t), (10.2.14)
j=1
т.
е.
общая
интенсивность
вЪtбытuя
является
суммой
частных
интенсивностей
вы
бытия
по
каждой
из
т
причин.
Мы
можем
свести
здесь
воедино
введенные
определения,
выразив
совместную
«плотность»,
маргинальную
функцию
вероятностей
и
маргинальную
плотность
в
актуарных
обозначениях,
причем
мы
сохраняем
номера
соответствующих
формул,
добавив
к
ним
«штрих»:
fT,J(t,j)
=
tP~T)J1.<j)(t)
fJ (j) =
ooq~j)
,
fr(t)
=
tP~T)
J1.~T)
(t).
(10.2.11')
(10.2.4')
(10.2.8/)

280
Гл.
10.
Модели
выбытия
по
нескольким
причинам
Условная
функция
вероятностей
С.в.
J
при
условии,
что
выбытие
произошло
в
мо
мент
времени
t, -
это
f
(t')
(Т)
(j)
(t)
и)
(t)
fJITUlt)
=
T,J
,)
=
tP~
)jJ~)
_
jJ~).
(10.2.15)
fT(t)
tPx
T
jJx
T
(t)
jJx
T
(t)
Наконец,
заметим,
что
вероятность,
определенная
формулой
(10.2.3),
может
быть
переписана
в
виде
tq!1)
= 1
!
.p~T)
1'!1)(s)
ds. (10.2.16)
Пример
10.2.1.
Рассмотрим
модель
выбытия
по
двум
причинам
с
интенсивно
стями
выбытия
jJ~l)
(t) =
t/l00,
t
~
О,
jJ~2)
(t) = 1/100, t
~
О.
Вычислим
для
этой
модели
функции
вероятностей
(или
функции
плотности)
сов
местных,
маргинальных
и
условных
распределений.
Решение.
Поскольку
jJ~T)(S)
=
jJ~l)(S)
+
jJ~2)(s)
=
(В
+1)/100,
вероятность
дожития
tP~T)
представляется
в
виде
t
;?;
О,
(Т)
_
(_
[t S +1 ) _ ( _ t
2
+
2t)
tP
x
-
ехр
Jo
100 ds -
ехр
200'
а
функция
«плотности»
совместного
распределения
С.в.
Т
и
J -
в
виде
fT,J(t,j)
=
t
(t
2
+
2t)
100
ехр
- 200 '
1
(t
2
+
2t)
100
ехр
- 200 '
t
~
О,
j = 1,
t
~
О,
j =
2.
Функцию
плотности
С.В.
Т
можно
записать
в
виде
2 . t+1
(t
2
+
2t)
!T(t)
=
f;;
!T,J(t,J) = 100
ехр
- 200 '
t
;?;
О,
а
функцию
вероятностей
С.В.
J -
в
виде
fJ(j)
=
{Jo:
fT,J(t,
1)
dt, j =
1,
Jo
fT,J(t, 2) dt, j = 2.
Функцию
fJ(2)
вычислить
легче.
В
дальнейшем
изложении
Ф(х)
-
функция
распре
деления
стандартного
нормального
закона
N(O, 1).
Дополняя
до
полного
квадрата,
получим
1
100
[(t
+ 1)2]
f
(2)
= -
е
О
,005
ехр
- dt
J 100
о
200
1
100
1 [
(t
+
1)
2]
= -
е
О
,005...[2;
10
ехр
- dt.
100
о
...[2;
10
200
