Бауэрс Н., Гербер Х., Джанс Д., Несбитт С., Хикман Дж. Актуарная математика
Подождите немного. Документ загружается.


Упражнения
231
к
~
h
-1,
K=h,
к;;;:
h+
1.
Дайте
словесную
интерпретацию
этих
формул.
8.9.
Покажите,
что
если
bh+l =
h+lV,
oV
=
о
и
1rh
=
1r
при
h =
0,1,
...
, k - 1,
ТО
kV =
1rSkj'
[Указание.
Используйте
формулу
(8.3.14).]
8.10.
Покажите,
что
если
1r -
постоянная
ежегодная
нетто-премия
по
договору
стра
хования
на
срок
n
лет
из
формулы
(8.3.14)
при
b
h
=an_hl' h =
1,2,
...
,П,
и
oV =
nV
=
О,
то
.. ..
( )
ащ
-
ах:П1
(Ь)
V····
..
а
1r
=..
, k =
an-kl-
ax+k:n-kl-
1ra
x
+
k
:
n
_
k
l'
а
х
:П1
[Указание.
Это
можно
показать
непосредственно
или
вывести
с
помощью
формулы
(8.3.10).]
К
разделу
8.4
8.11.
Начав
с
формулы
(8.4.3),
докажите
равенство
spx+h
h+s
V +
vl-s
sqx+h bh+l =
(1
+
i)S(hV
+
'7Гh),
о
< s < 1.
Объясните
этот
результат
с
помощью
общих
соображений.
8.12.
Дайте
интерпретацию
формул
( )
V
(m)
(1
h )
V(m)
( h )
V(т)
( 1 )
р(т)
а
k+(h/m}+r
~
-
т
- r k +
т
+r k+l +
т
- r ,
(»)
H(h/m)+,V{m}
'"
(1
-
~
-
')
<у{т}
+
(~
+
')
k+,V{m}
+
(~
-
')
р{т}
,
где
О
< r <
1/
m.
8.13.
Для
каждого
из
следующих
нетто-резервов
найдите
формулы,
аналогичные
од
ному
или
нескольким
из
равенств
(8.4.8), (8.4.14)
и
(8.4.18):
- -
(2)
-
(а)
20!
V(A
x
:
4Ol
),
(Ь)
20!
V(A
x
:
4Ol
),
(с)
20!V
(A
x
:
4Ol
),
(2)
-
{2}
-
{2}
-
(d)
20jV
(A
x
:
4Ol
),
(е)
20!V
(А
х
:
4О1
)
,
(f)
20iV
(А
х
:
4OI
),
8.14.
Пользуясь
Иллюстративной
таблицей
смертности
и процентной
ставкой
6%,
по
лучите
аппроксимацию
выражения
10!V{4}(,,42S).
к
разделу
8.5
8.15.
Покажите,
что
для
договора
бессрочного
страхования
на
случай
смерти
с
выпла
той
размера
1
в
дискретной
модели и
с
премиями,
выплачиваемыми
пожизненно,
заклю
ченного
с
лицом
(х),
(а)
D[L] = f
(ii
X
:'-h+l)
2v
2
(h+l) hpx Px+h qx+h,
h=O
ах
(Ь)
D[kLIK(x)
~k]
=f
(ii
x
+:+
h
+
1
)
2
V2
(h+l)hPX+kPX+k+h qx+k+h·
h=O
Х
8.16.
Для
страхового
аннуитета
пренумерандо
с
ежегодными
выплатами
размера
1,
производящимися
до
тех
пор,
пока
лицо
(х)
живо,
рассмотрите
потери
L=ak+11-iiх,
К=0,1,2,
...
,
и
потери
Ah,
вычисленные
на
момент
времени
h,
которые
соответствуют
году
h
выплаты
аннуитета,
а
именно
{
О,
Ah =
-(ax+h
- 1) =
-Vpx+h
ii
x
+h+l,
Vii
x+h+l - (iix+h - 1) =
vQx+h
ii
x
+h+l,
(а)
Дайте
интерпретацию
формуд
для
Ah.
(Ь)
Покажите,
что
ею
(i) L = L v
k
A
h
,
(Н)
E[AhJ =
о,
(iii) D[Ah] = v
2
(ii
x
+h+l)2hpx px+h
Qx+h.
h=O

232
Гл.
8.
Анализ
нетто-резервов
К(х)
= k, k +
1,
...
, k +h -
1,
К(х)
=k+h,
К(х)
= k +h +
1,
k +h +
2,
....
8.17.
(а)
Для
договора
страхования
из
примера
8.3.2
покажите, что
n-l
D[LJ
=
.L
v
2
(h+l)
hPx
Px+h
Qx+h'
h=O
(Ь)
При
д
=0,05, n =
20
и
J.Lx(t)
=0,01, t
~
О,
вычислите
величину
D[L]
для
договора
страхования
из
п.
(а).
8.18.
Договор
бессрочного
страхования
на
случай
смерти
с
выплатой
размера
1
и
20-летним
периодом
выплаты
премий,
заключенный
с
лицом
25
лет,
рассматривается
в
дискретной
модели.
На
основе
Иллюстративной
таблицы
смертности
и
процентной
ставки
6%
рассчитайте
(а)
ЗО
Р
25,
(Ь)
~gV25,
(с)
~8V25,
(d) D[20LIK(25)
~20],
(е)
D[lSLIK(25)
~
18].
К
разделу
8.6
8.19.
Дайте
интерпретацию
дифференциальных
уравнений
d-
-
d-
- -
(а)
dt tV
=?Те
+
[8
+
J.Lx(t)]
tV - b
t
J.Lx(t),
(Ь)
dt tV
=?Те
+8
tV
-
(b
t
-
tV)J.Lx(t).
8.20.
Покажите,
что
t17
=
?т
Stj
для
b
t
=tV,
017
=
О
и
nt
=
?т,
t
~
О.
d - -
8.21.
Вычислите
dt
{[1
-
tV(A
x
)]
tPx}.
8.22.
Используя
формулу
(8.6.2),
выразите
d - d
е-
d t -
(а)
dt
(фх
tV),
(Ь)
dt
(v
tV),
(с)
dt
(v
tpx tV)
и
дайте
интерпретацию
полученных
результатов.
Ко
всем
темам
гJl.aвь&
8.23.
Покажите,
что
формула,
эквивалентная
формуле
(8.4.6)
в
предположении
о
ги
перболичности
распределения
смертей
в
течение
годичных
возрастных
интервалов,
-
это
k+s
V =v
1
-
s
[(1
- S)(kV +nk)(1 +i) +s k+l
VJ.
8.24.
Покажите,
что
foOO
[v
t
-
Р(Л
ж
)аl]]2
tРж
IJж
(t) dt =
fooo
[1
-
tV(А
ж
)]2
v
2t
tpx
J.Lж(t)
dt
и
дайте
интерпретацию
этого
результата.
8.25.
Для
получения
другой
формы
теоремы
Хаттендорфа
рассмотрим
следующие
случайные
величины:
(
ЬК+l
v(K-k)+l - kV -
Ktk
Jrk+h
v
k
,
К(х)
=k, k +
1,
...
,k
+
т
- 1,
L -
h=O
k,m
-
m-l
k+mV v
m
- kV -
Е
nk+h
v
h
,
К(х)
= k +
т,
k +
т
+1,
...
I
h=O
И
для
h =
О,
1,
...
,
т
- 1
{
О,
Ak+
h
= V
bk+h+l
-
(k+h
V +
Jrk+h)
,
V k+h+lV -
(k+h
V +nk+h),
Покажите,
что
m-l
m-l
(а)
k,mL=
LvhЛk+h,
(Ь)
DkmLIK(x)~k]=
LV2hD[Ak+hIK(x)~k].
h=O
h=O
8.26.
Проведите
рассуждения
примера
8.5.1
для
страхователя
из
примера
7.4.4,
кото
рый
дожил
до
конца
второго года
действия
договора.
8.27.
Проведите
рассуждения
примера
8.5.2
для
портфеля
из
1500
договоров
того
же
типа,
что
описывались
в
примере
7.4.4
и
обсуждались
в
упр.
8.26.

'Упражнения
23З
8.28.
В
упр.
8.27
отсутствовала
неопределенность
относительно
суммы
или
времени
выплаты
ДЛЯ
страхователей,
которые
дожили
до
конца
четвертого
года
действия
договора.
Проделайте
упр.
8.27
для
доживших
до
конца
2-го
и
3-го
года.
8.29.
Запишите
в
терминах
нетто-премий
и
конечных
нетто-резервов
формулу
нетто
резерва
на
середину
11-
го
страхового
года
для
договора
бессрочного
страхования
на случай
смерти
со
страховой
выплатой
размера
10000
и
с
ежегодНЫМИ
премиями
с
корректирую
щим
платежом, заключенного
с
лицом
(ЗО).
8.ЗО.
По
договору
смешанного
страхования
на
срок
3
года
со
страховой
суммой
раз
мера
3
выплаты
на
случай
смерти
осуществляются
в
конце
года
смерти,
а
нетто-премии
размера
0,94
выплачиваются
ежегодно.
При
процентной
ставке
20%
были
получены
сле
дующие
резервы:
Конец
года
1
2
З1
Нетто-резерв
0,66
1,56
3,00
Подсчитайте
(а)
qx,
(Ь)
qx+l,
(с)
дисперсию
потерь
oL
на
момент
заключения
договора,
(d)
дисперсию
потерь
lL
на
конец
первого
года
действия
договора.
8.31.
(а)
Используйте
формулу
(8.3.10),
чтобы
преобразовать
формулу
(8.5.1)
к
виду
{
О,
К(х)
~
h
-1,
A
h
= (bh+l - h+1V)V - (bh+l - h+lV)vqx+h,
К(х)
=
h,
0-
(bh+l - h+lV)Vqx+h,
К(х)
~
h +
1.
В
этой
интерпретации
С.в.
Л
h
представляет
собой
потери,
связанные
с
обязательствами
по
страхованию
сроком на
1
год
и
страховой
выплатой
размера
рисковой
суммы
в
году
(h, h +1).
(Ь)
Используйте
выражение
из
п.
(а)
для
проверки
равенства
Е[ЛhJ
=
о.
(с)
Используйте
результаты
пп.
(а)
и
(Ь)
дЛЯ
вычисления
величины
D[Л
h
].
Уnра::нсн.ен:u.я
с
исnользование,м
7Со,мnъюmера
8.32.
Рассмотрим
дисперсию
для
договора
бессрочного
страхования
на
случай смерти
из
примера
8.2.2,
заключенного
с
лицом
(20),
с
выплатой
на
случай
смерти,
размер
которой
равен
1,
и
с
возрастающими
в
геометрической
прогрессии
нетто-премиями,
выплачиваемы
ми
до
возраста
65
лет.
Воспользовавшись
Иллюстративной
таблицей
смертности
и
полагая
i = 0,06,
определите
такое
максимальное
значение
т,
чтобы
нетто-резерв
был
неотрица
тельным
для
всех
моментов
времени.
8.33.
Используйте
обратную
рекуррентную
формулу
(8.3.9)
для
расчета
нетто-резер
вов
в
(а)
примере
7.4.3
[указание:
5V
=
O,OJ,
(Ь)
примере
7.4.4
[указание:
5V
=1,0).
8.34.
Договор
страхования,
заключенный
с
лицом
(30)
на
срок
до
достижения
им
возраста
65
лет
с
уменьшающейся
страховой
выплатой,
которая производится
в
момент
смерти,
предусматривает
следующие
страховые
выплаты:
В
случае
смерти
между
возрастами
ЗО-50
50-55
55-60
60-65
Выплата
100000
90000
80000
60000
На
основе
Иллюстративной
таблицы
смертности
в
предположении
равномерности
рас
пределения
моментов
смерти
в
каждом
ГОдИчном
возрастном
интервале и
при
i = 0,06
определите

234
Гл.
8.
Анализ
нетто-резервов
(а)
годовую нетто-премию
с
корректирующим
платежом
при
выплате
дважды
в
год
в
полунепрерывной
модели,
(Ь)
резерв
на
конец
30-го
года
ДЛЯ
премии
из
п.
(а).
8.35.
Договор
страхования
с
единовременной
премией,
заключенный
с
лицом
(35),
обеспечивает
выплату
размера
100000,
если
страхователь
доживет
до
возраста
65
лет,
или
возврат
единовременной
нетто-премии
без
начисления
процента
в
конце
года
смерти,
если
он
умрет
до
достижения
им
возраста
65
лет.
Обозначив
единовременную
нетто-премию
через
S,
выразите
через
актуарные
функции
(а)
S,
(Ь)
перспективную
формулу
для
нетто-резерва
на
конец
k-ro
года,
(с)
ретроспективную
формулу
для
нетто-резерва
на
конец
k-ro
года.
(d)
Вычислите
с.в.
S
и
нетто-резерв
2
0
V,
применяя
Иллюстративную
таблицу
смерт
ности
и полагая
d =0,05.
8.36.
В
терминах
Р
=
20р(12)
(..430:351)
И
актуарных
функций
выведите
перспективные
и
ретроспективные
формулы
для
следующих
резервов:
( )
20V(12)
(А-
)
(Ь)
20V(12)
(А-
)
а
10
30:351 ,
25
З0:35l
.
(с)
Вычислите
Р
и
нетто-резервы
из
пп.
(а)
и
(Ь)
на
основе
Иллюстративной
таблицы
смертности
в
предположении
равномерности
распределения
моментов
смерти
в
каждом
годичном
возрастном
интервале
и
при
0=0,05.

9
АКТ"УАРНЫЕ
ФУНКЦИИ
ДЛЯ
НЕСКОЛЬКИХ
ЛИЦ
9.1.
Введение
в
гл.
с
3
по
8
мы
развивали
теорию,
позволяющую
анализировать
денежные
вы
платы,
зависящие
от
момента
смерти
отдельного
лица.
Можно
обобщить
эту
теорию
на
случай
выплат,
связанных
с
несколькими
лицами.
Одним
из
приложений
тако
го
обобщения,
часто
применяемым
в
пенсионных
схемах,
являются
пожизненные
аннуитеты
в
пользу
двух
и
более
лиц.
Общеизвестны
другие
приложения
актуар
ных
расчетов
для
группы
лиц.
Например,
они
применяются
при
налогообложении
имущества
и
дарений.
Скажем,
инвестиционный
доход
от
имущества,
переданного
в
доверительное
управление,
выплачивается
группе
наследников
до
тех
пор,
пока
жив
последний
из
них.
После
смерти
последнего
наследника
капитал
изымается
из
дове
рительного
управления
и
передается
в
дар
благотворительной
организации.
Вели
чина
налогового
вычета,
связанного
с
благотворительностью,
при
налогообложении
этого
дара
будет
определяться
актуарными
расчетами.
Существуют
договоры
се
мейного
страхования,
в
которых
предусмотрены
различные
выплаты
в
зависимости
от
того,
в
какой
последовательности
умирают
страхователь
и
его
супруга.
Суще
ствуют
также
договоры
с
выплатами
на
случай первой
или
последней
смерти
для
возмещения
взносов
по оплате
недвижимости.
В
настоящей
главе
мы
рассмотрим
модель
с
двумя
лицами.
Актуарные
насто
ящие
стоимости
основных
видов
выплат
выводятся
с
помощью
понятий
И
методов,
изложенных
в
гл.
3-5.
Б6льшая
часть
этой
главы
посвящена
модели,
основанной
на
предположении,
что
две
рассматриваемые
случайные
величины
продолжительно
сти
предстоящей
жизни
независимы.
В
разд.
9.6
исследуются
специальные
модели,
в
которых
эти
две
случайные
величины
зависимы.
Ежегодные
премии,
резервы
и
модели
для
трех
и
более
лиц
рассматриваются
в
гл.
18.
Полезной
абстракцией
теории
страхования
жизни,
особенно
при
рассмотрении
групп
лиц,
является
понятие
статуса,
для
которого
введены
понятия
сохранения
и
потери.
Для
того
чтобы
ввести
определение
статуса,
необходимо
два
элемента.
Во-первых,
это
общий
термин
обlJе-х:т,
который
используется
в
силу разнообразия
практических
приложений:
•
множество
объектов
должно
быть
конечным
и
для
каждого
из
элементов
этого
множества
необходимо
уметь
определять
случайную
величину
продолжительности
предстоящей
жизни
.
•
должно
существовать
правило,
позволяющее
устанавливать
факт
сохранения
статуса
в
любой
момент
времени
в
будущем.
Для
того
чтобы
рассчитать
вероятности
или
актуарные
настоящие
стоимости,
связанные
с
сохранением
некоторого
статуса,
необходимо
иметь
совместное
распре
деление
случайных
величин
продолжительности
предстоящей
жизни.
Некоторые
из

236
Гл.
9.
Актуарные
функции
для
нескольких
лиц
о
< s < 10,
О
< t < 10,
в
остальных
случаях.
этих
случайных
величин
могут
иметь
маргинальное
распределение,
сосредоточенное
в
одной
точке.
Полезно
проиллюстрировать
понятие
«статус»
несколькими
примерами.
Отдель
ное
лицо
возраста
х
лет
определяет
некоторый
статус,
который
сохраняется,
пока
это
лицо
живо.
Таким
образом,
случайную
величину
Т(х),
использованную
в
гл.
3
для
обозначения
продолжительности
предстоящей
жизни
лица
(х),
можно
интер
претировать
как
продолжительность
периода
сохранения
этого
статуса,
а
также
как
продолжительность
предстоящего
периода
до
момента
потери
статуса.
Срок
до
мо
мента
n,
ffi,
определяет
некоторый
статус,
который
сохраняется
ровно
n
лет,
а
за
тем
теряется.
Для
нескольких
лиц
различными
способами
можно
определить
более
сложные
статусы.
Сохранение
статуса
можно
понимать
как
дожитие
всех
лиц
из
группы
или,
напротив,
как
дожитие
хотя
бы
одного
лица
из
группы.
Для
группы,
в
которую
входят
два
мужчины
и
две
женщины,
можно
определять
и
более
слож
ные
статусы.
Например,
статус
сохраняется
лишь
до
тех
пор,
пока
живы
по
крайней
мере
один
мужчина
и
по
крайней
мере
одна
женщина.
После
того
как
статус
и
критерий
его
сохранения
определены,
мы
можем
приме
нить
это
определение
к
построению
моделей
аннуитетов и
договоров
страхования.
Аннуитет
выплачивается
до
тех
пор,
пока
статус
сохраняется,
а
выплаты
по
догово
ру
страхования
производятся
после
потери
статуса.
В
договорах
страхования
также
могут
быть
оговорены
условия,
согласно
которым
выплаты
производятся
лишь
то
гда,
когда
лица,
к
которым
относится
договор,
умирают
в
определенной
последова
тельности.
9.2.
Совместное
распределение
продолжительностей
предстоящей
жизни
Время
до
потери
некоторого
статуса
является
функцией
продолжительностей
предстоящей
жизни
рассматриваемых
лиц.
С
теоретической
точки
зрения
эти
про
должительности
будут
зависимыми
случайными
величинами.
Мы
изучим
послед
ствия такой
зависимости.
Для
удобства
или
из-за
отсутствия
данных
о
зав,ИСИМОСТИ
между
лицами
на
практике
обычно
принимается
предположение
о
независимости
рассматриваемых
продолжительностей
предстоящей
жизни.
Принимая
такое
пред
положение,
можно
пользоваться
численными
значениями,
полученными
из
марги
нальных
распределений
(таблиц
смертности)
для
отдельных
лиц.
Пример
9.2.1.
Хотя
распределение,
рассматриваемое
в
этом
примере,
не
реали
стично,
оно
приведено
как
средство
исследования
совместного
распределения
двух
зависимых
случайных
величин
продолжительности
предстоящей
жизни.
Для
двух
лиц
(х)
и
(у)
совместная
функция
плотности
с.в.
Т(х)
и
Т(у)
продолжительностей
их
предстоящей
жизни
имеет
вид
f
(
t) -
{0,0006(t
-
8)2,
Т(х)Т(у)
8,
-
О
Определим:
(а)
совместную
функцию
распределения
С.В.
Т(х)
и
Т(у);
(Ь)
функцию
плотности,
функцию
распределения,
sPx
и
р,(х
+
В)
дЛЯ
марги
нального
распределения
С.в.
Т(х).
Обратим
внимание
на
симметрию
выписанного
распределения
относительно
s
и
t,
откуда
следует,
что
С.в.
Т(х)
и
Т(у)
одинаково
распределены;
(с)
коэффициент
корреляции
между
С.в.
Т(х) и
Т(у).
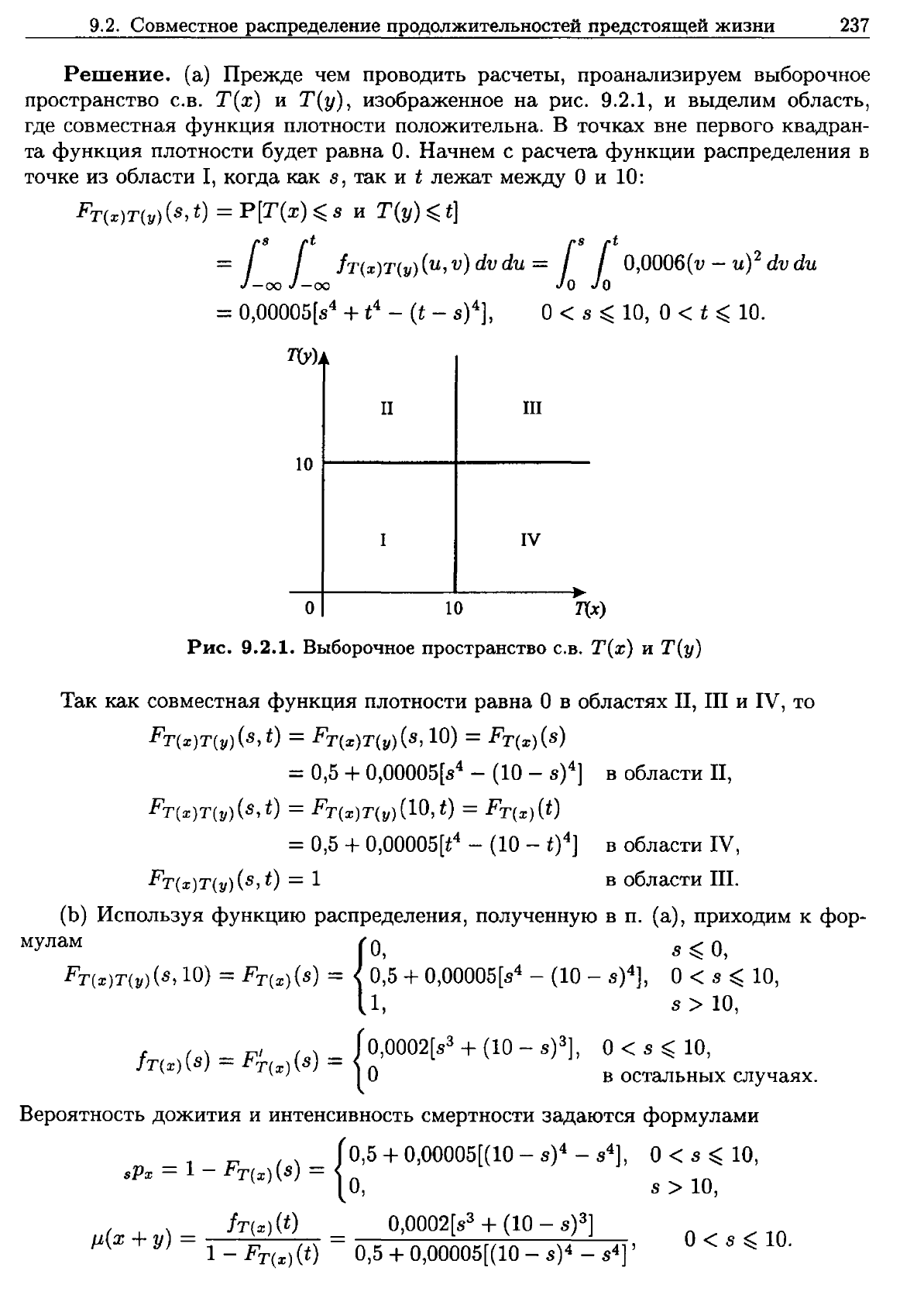
9.2.
Совместное
распределение
продолжительностей
предстоящей
жизни
237
Решение.
(а)
Прежде
чем
проводить
расчеты,
проанализируем
выборочное
пространство
С.в.
Т(х)
и
Т(у),
изображенное
на
рис.
9.2.1,
и
выделим
область,
где
совместная
функция
плотности
положительна.
В
точках
вне
первого
квадран
та
функция
плотности
будет
равна
О.
Начнем
с
расчета
функции
распределения
в
точке
из
области
1,
когда
как
8,
так
и
t
лежат
между
О
и
10:
FT(x)T(y)
(8,
t)
=
Р[Т(х)
~
8
и
Т(у)
~
t]
=
{8
{t
fT(x)T(y)(u,v)dvdu=
{8
{t
o
,0006(V-u)2dvdu
J-oo
J-oo
J
o
J
o
= 0,00005[84 +t
4
-
(t - 8)4],
О
< 8
~
10,
О
< t
~
10.
1{y)~
II
III
10
1------+------
о
1
10
IV
,
т(х)
Рис.
9.2.1.
Выборочное
пространство
С.В.
Т(х)
и
Т(у)
Так
как
совместная
функция
плотности
равна
О в
областях
11,
111
и
IV,
то
FT(x)T(y)
(8,
t) =
FT(x)T(y)
(8,
10) =
FT(x)
(8)
= 0,5 +0,00005[84 - (10 -
8)4]
в
области
11,
FT(x)T(y)
(8,
t) =
FT(x)T(y)
(10, t) =
FT(x)
(t)
= 0,5 +0,00005[t
4
-
(10 -
t)4]
в
области
IV,
FT(x)T(y)
(В,
t) = 1
в
области
111.
(Ь)
Используя
функцию
распределения,
полученную
в
п.
(а),
приходим
к
фор-
мулам
{О
8
~
О
,
~
,
FT(x)T(y)
(8, 10) = F
T
(x)(8)
= 0,5 +0,00005[84 - (10 -
8)4J,
О
< 8
~
10,
1,
8 > 10,
fT
х
(8)
= R'
(8)
=
{0,0002[В
3
+ (10 -
8)3],
0<8
~
10,
( )
Т(х)
О
В
остальных
случаях.
Вероятность
дожития
и
интенсивность
смертности
задаются
формулами
_ 1 D
()
_
{0,5
+0,00005[(10 -
8)4
-
84],
0<8
~
10,
вРх
- -
ГТ(х)
8 -
О,
8 > 10,
(
)
fT(x)(t)
0,0002[83 + (10 -
8)3]
jL
Х
+
у
= ( )
[()4
4'
О
< 8
~
10.
1 -
FT(x)
t 0,5 +0,00005 10 - 8 - 8 ]

238
Гл.
9.
Актуарные
функции
для
нескольких
лиц
(с)
Е[Т(х)]
=
["
8(0,0002)[83 +(10 - 8)3]
d8
=5 =
Е[Т(у)],
{10
110
Е[т(х)2]
=
J(}
82(0,0002)[83 + (10 -
8)3]
d8
=3 =
Е[Т(у)2],
О
35
D[T(x)] = 3 = D[T(y)],
Е[Т(х)Т(у)]
=
["
["
8t(0,0006)(t -
8)2
d8
dt
=
5;,
25
Cov[T(x),
Т(у)]
=
Е[Т(х)Т(у)]
-
Е[Т(х)]Е[Т(у)]
=
-3'
Cov[T(x),
Т(у)]
-25/3
5
~
Рт(х)т(у)
=
ат(х)ат(у)
=
35/3
=
-7
.
Исходя
из
совместного
распределения
С.в.
Т(х) и
Т(у),
определим
совместную
фу'Н~'Ц'Uю
до;жuтu-я
следующим
образом:
ST(x)T(y)(8,
t)
=
Р(Т(х)
>8 n
Т(у)
>
t].
(9.2.1)
В
отличие
от
одномерного
случая,
сумма
совместной
функции
распределения
и
сов
местной
функции
дожития
не
обязательно
равна
1.
Связь
между
ними
можно
про
иллюстрировать,
изобразив
совместное
выборочное
пространство
С.В.
Т(х)
и
Т(у)
на
рис.
9.2.2.
Функция
распределения
FT(x)T(y)(S,
t)
определяет
вероятности
для
та
ких
областей,
как
А,
«юго-западнее»
точки
(8,
t),
а
функция дожития
8т(х)т(у)
(8,
t)
-
вероятности
для
таких
областей,
как
В,
«северо-восточнее.
точки
(8,
t).
1tY)
Область
В
(8,
t)
t
Область
А
о
8
т(х)
Рис.
9.2.2.
Выборочное
пространство
С.В.
Т(х)
И
Т(у),
продолжительностей
предстоящей
жизни
Пример
9.2.2.
Определим
совместную
функцию
дожития
для
С.в.
Т(х) И
Т(у)
из
примера
9.2.1.
Решение.
При
О
< 8 <
10
и
О
< t <
10
ST(x)T(y)(8,
t) =
Р[Т(х)
>8 n
Т(у)
>
t]
{ОО
100
(10
110
=
J8
t
fT(x)T(y)(U,
v)
dv
du
=
J8
t 0,0006(v -
u)2
dv
du
= 0,00005[(10 -
t)4
+(10 -
8)4
-
(t
-
8)4J.

9.2.
Совместное
распределение
продолжителъностей
предстоящей
жизни
239
Для
других
точек
из
первого
квадранта
функция
SТ(ж)Т(у)(S,
t)
равна
О,
а
для
всех
точек
из
третьего
квадранта
она
равна
1.
Во
втором
квадранте,
где
s <
О
и
t >
О,
SТ(ж)Т(у)
(s, t) =
ST(y)
(t) =tPy·
в
четвертом
квадранте,
где
в
>
О
и
t <
О,
ST(x)T(y)
(в,
t) =
ВТ(ж)(В)
=
tРж·
у
В
примере
9.2.1
было
задано
совместное
распределение
двух
зависимых
слу
чайных
величин
продолжительности
предстоящей
жизни,
а
затем
определены
их
маргинальные
распределения
и
найден
коэффициент
корреляции
между
ними,
яв
ляющийся
мерой
их
зависимости.
В
практических
приложениях
может
оказаться,
что
выразить
зависимость
между
продолжительностями
предстоящей
жизни
числом
сложно.
Поэтому
такие
случайные
величины
обычно
предполагаются
независимыми,
а
тогда
их
совместное
распределение
получается
из
соответствующих
маргинальных
распределений,
которые
мы
обсуждали
в
гл.
3.
Это
иллюстрируется
следующим
при
мером.
Пример
9.2.3.
Случайные
величины
продолжительности
предстоящей
жизни
Т(х)
и
Т(у)
независимы,
и
распределение
каждой
их
них
определено
функцией
плотности
t
~
О,
О
< t
~
10,
t>
10,
t <
О,
О
~
t < 10,
t
~
10,
0<
t < 10.
f(t)
= {00,02(10 -
t),
О
< t < 10,
в
остальных
случаях.
(а)
Определим
функцию
распределения,
функцию
дожития
и
интенсивность
смертности
в
этом
случае.
(Ь)
Определим
совместную
функцию
плотности,
совместную
функцию
распре
деления
и
совместную
функцию
дожития
для
С.в.
Т(х)
И
Т(у).
Решение.
jt
{О,
(а)
Fт(ж)(t)
=
с
fт(ж)(S)
dB
= 1 - 0,01(10 - t)2 =0,2t - 0,Olt
2
,
-00
1
,
{
1'
ВТ(ж)
(t) = 1 -
РТ(х)
(t)
= 0,01(10 - t)2,
О,
р(х
+
t)
=
fт(ж)(t)
2,
ВТ(х)
(t) 10 - t
(Ь)
fт(ж)т(у)(в,t)
=
fт(ж)
(S)fT(y) (t)
= {
~0,02)2(1O
- 8)(10 - t),
РТ(х)Т(у)
(В,
t) =
РТ(х)
(s)FT(y) (t)
= (0,2)2(t - 0,05t
2
)(s -
0,05в
2
),
=FT(x)(s) =
(0,2)(в
-
0,05в
2
),
=
РТ(у)
(t) = (0,2)(t - 0,05t
2
),
О
<
В
< 10,
О
< t < 10,
в
остальных
случаях,
о
< S
~
10,
О
< t
~
10,
О
<
В
~
10, t > 10,
В
> 10,
О
< t
~
10,

240
Гл.
9.
Актуарные
функции
ДЛЯ
нескольких
лиц
8T(x)T(y)(8,t)
=
8т(х)
(8)8т(у)
(t)
= (0,01)2(10 - 8)2(10 - t)2,
=
8Т(х)(8)
= (0,01)(10 -
8)2,
=
8т(у)
(t)
==
(0,01)(10 -
t)2,
=0,
о
~
8 < 10,
О
~
t < 10,
О
~
8 < 10, t <
О,
8 <
О,
О
~
t < 10,
8
~
10, t
~
10.
9.3.
Статус
дожития
всех
лиц
из
группы
Статус,
который
сохраняется,
пока
все
члены
группы
живы,
и
теряется
после
первой
смерти,
называется
статусо,м,
дОaICития
всех
лиц
из
группы.
Он
обозначает
ся
символом
(ХIХ2
•••
Х
т
),
где
Xi
-
возраст
i-ro
члена
группы,
а
т
-
число
членов.
В
этой
ситуации
используются
обозначения,
введенные
в
гл.
3-5,
но
вместо
возраста
одного
страхователя
в
нижнем
индексе
стоит
перечень
возрастов
членов
группы.
Например,
Аху
и
tPxy
имеют
тот
же
смысл
для
статуса
(ху)
дожития
двух
лиц
(х)
и
(у),
что и
Ах
и
tPx
-
для
одного
лица
(х).
Статус
дожития
всех
лиц
из
группы
является
примером статуса
дожития,
т.
е.
статуса,
для
которого
определена
случайная
величина
продолжительности
его
сохранения
и,
следовательно,
функция
дожития.
Для
продолжительности
предсто
ящего
периода
сохранения
статуса
дожития
применимы
понятия
и
соотношения,
рассматривавшиеся
в
разд.
с
3.2.2
по
3.5
(за
исключением
примера таблицы
смерт
ности
в
разд.
3.3.2),
которые
будут
использоваться
здесь
без
новых
доказательств.
Теперь
рассмотрим
распределение
случайной
величины
продолжительности
предстоящего
периода
сохранения
статуса
дожития
всех
лиц
из
группы.
Для
т
лиц
имеет
место
равенство
T(XIX2'"
Х
т
)
=
min[T(xl),
Т(Х2),""
Т(х
т
)],
где
T(Xi)
-
момент
смерти
лица
с
номером
i.
Для
частного
случая
двух
лиц,
(Х)
и
(у),
име
ем
Т(ху)
=
min[T(x),T(y)].
Когда
это не
может
вызывать
недоразумений,
будем
обозначать
эту
случайную
величину
просто
через
Т.
Специалист
может
заметить,
что
продолжительность
предстоящего
периода
сохранения
статуса
дожития
всех
лиц
из
группы
является
наu.м,енъшеЙ
порядковой
статистuкой,
образованной
т
случайными
величинами
продолжительности
предстоящей
жизни
лиц
из
группы.
При
исследовании
порядковых
статистик
случайные
величины
в
выборке
обычно
предполагаются
независимыми
и
одинаково
распределенными.
В
нашей
же
ситуа
ции
такие
случайные
величины,
как
правило,
считаются
независимыми,
но
редко
бывают
одинаково
распределены.
Мы
начнем
с
того,
что
выразим
функцию
распределения
С.в.
Т
для
t >
О
в
терминах
совместного
распределения
пары
с.в.
Т(х)
и
Т(у)
в
общем
(при
наличии
зависимости
между
ними)
случае:
FT(t)
= tQxy =
Р(Т
~
t) =
P{min[T(x),
Т(у)]
~
t}
= 1 -
P{min[T(x),
Т(у)]
>t}
= 1 -
Р{Т(х)
>t n
Т(у)
>t} = 1 -
8T(x)T(y)(t,
t).
(9.3.1)
Другое
равенство
может
быть
получено
из
первой строки
с
учетом
того,
что
событие
{min[T(x),
Т(у)]
~
t}
является
объединением
событий
{Т(х)
~
t}
и
{Т(х)
~
t}.
Тогда
FT(t)
=
P{min[T(x),
Т(у)]
~
t},
