Бауэрс Н., Гербер Х., Джанс Д., Несбитт С., Хикман Дж. Актуарная математика
Подождите немного. Документ загружается.

7.2.
Нетто-резервы
в
непрерывной
модели
191
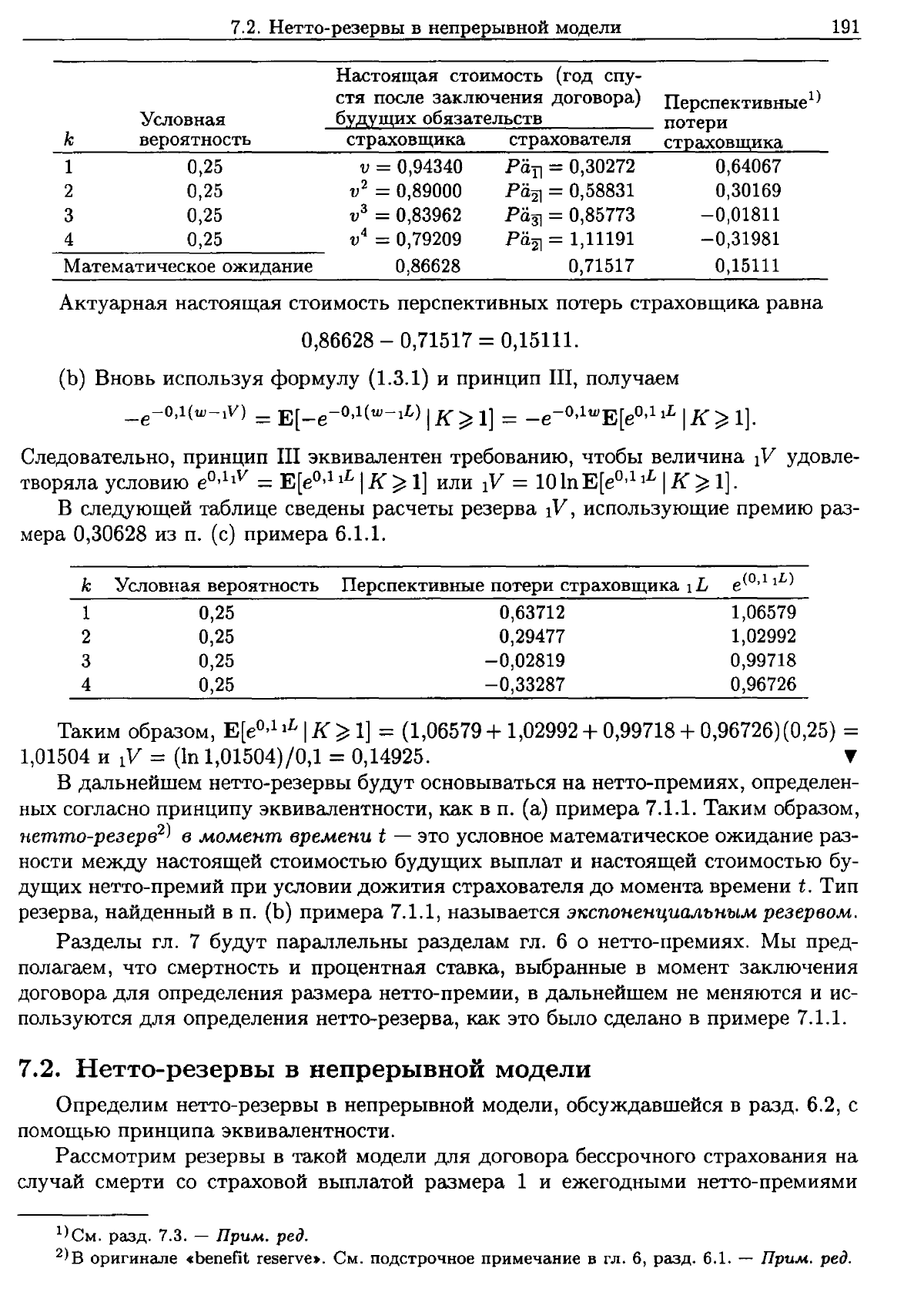
Условная
k
вероятность
1 0,25
2 0,25
3 0,25
4 0,25
Математическое
ожидание
Настоящая
стоимость
(год
спу-
стя
после
заключения
договора)
Перспективные
1
)
~бУ..иД::::loУL.:щ=и::..:х~о::...:б:..::я:.::з-=а.::...те=л-=ь::.;:с;.::т-=в_____
потери
страховщика
страхователя
страховщика
v = 0,94340
PaТl
=0,30272 0,64067
у}2
=0,89000
Pa21
=0,58831 0,30169
v
з
= 0,83962
Ра31
= 0,85773 -0,01811
v
4
= 0,79209
Pa21
= 1,11191 -0,31981
0,86628 0,71517 0,15111
Актуарная
настоящая
стоимость
перспективных
потерь
страховщика
равна
0,86628 - 0,71517 =0,15111.
(Ь)
Вновь
используя
формулу
(1.3.1)
и
принцип
IП,
получаем
_e-O,l(w-N)
=
E[_e-
O
,1(w-
1
L)
I
к
~
1]
=
_e-О,lWЕ[еО,11L
I
к
~
1].
Следовательно,
принцип
111
эквивалентен
требованию,
чтобы
величина
lV
удовле
творяла
условию
eO,ll
V
=E[eO,1
1
L I
к
~
1]
или
lV
=10 lnE[eO,1
1
L I
к
~
1].
В
следующей
таблице
сведены
расчеты
резерва
1
V,
использующие
премию
раз
мера
0,30628
из
п.
(с)
примера
6.1.1.
k
1
2
3
4
Условная
вероятность
0,25
0,25
0,25
0,25
Перспективные
потери
страховщика
1L
0,63712
0,29477
-0,02819
-0,33287
1,06579
1,02992
0,99718
0,96726
Таким
образом,
E[eO,1
1
L I
к
~
1]
=(1,06579 +1,02992 +0,99718 +0,96726)(0,25) =
1,01504
и
lV
=(ln 1,01504)/0,1 =0,14925.
~
В
дальнейшем
нетто-резервы
будут
основываться
на
нетто-премиях,
определен
ных
согласно
принципу
эквивалентности,
как
в
п.
(а)
примера
7.1.1.
Таким
образом,
н,етто-резерв
2
)
в
,момент
вре,мени
t -
это
условное
математическое
ожидание
раз
ности
между
настоящей
стоимостью
будущих
выплат
и
настоящей
стоимостью
бу
дущих
нетто-премий
при
условии
дожития
страхователя
до
момента
времени
t.
Тип
резерва,
найденный
в
п.
(Ь)
примера
7.1.1,
называется
Э7Ссnонен.циа.лЬНЪL,м
резервом.
Разделы
гл.
7
будут
параллельны
разделам
гл.
6
о
нетто-премиях.
Мы
пред
полагаем,
что
смертность
и
процентная
ставка,
выбранные
в
момент
заключения
договора
для
определения
размера
нетто-премии,
в
дальнейшем
не
меняются
и
ис
пользуются
для
определения
нетто-резерва,
как
это
было
сделано
в
примере
7.1.1.
7.2.
Нетто-резервы
в
непрерывной
модели
Определим
нетто-резервы
в
непрерывной
модели,
обсуждавшейся
в
разд.
6.2,
с
помощью
принципа
эквивалентности.
Рассмотрим
резервы
в
такой
модели
для
договора
бессрочного
страхования
на
случай
смерти
со
страховой
выплатой
размера
1
и
ежегодными
нетто-премиями
l)CM.
разд.
7.3. -
Прu.,м.
ред.
2)в
оригинале
«benefit reserve•.
См.
подстрочное
примечание
в
ГЛ.
6,
разд.
6.1. -
Прu,м.
ред.

192
Гл.
7.
Нетто-резервы
Р(А[х])
,
заключенного
с
лицом
(х).
Соответствующий
резерв
для
страхователя,
про
жившего
еще
t
лет,
определяется,
согласно
принципу
эквивалентности,
как
условное
математическое
ожидание
перспективных
потерь
в
момент
времени
t
при
условии,
что
лицо
(х)
доживет
до
этого
момента.
Более
формально,
при
Т(х)
> t
перспек
тивные
потери
составят
L
-
T(x)-t
p~
(А-
)-
(7 2
1)
t - V -
[х]
aT(x)-tl'
..
Резерв
как
условное
математическое
ожидание
рассчитывается
на
основе
условного
распределения
продолжительности
предстоящей
жизни
в
момент
t
лица,
которое
прошло
селекцию
в
возрасте
х
лет,
при
условии,
ЧТО
оно
дожило
до
момента
време
ни
t.
Согласно
Международной
системе
актуарных
обозначений,
это
можно
записать
в
следующем
виде:
iV(.A(x])
=E[tL I
Т(х)
>
t]
= E[vT(x)-t I
Т(х)
>
t]
- P(A[x)E[aT(x)_tll
Т(х)
>
t]
=
A[x]+t
- P(A[x])a[x)+t.
(7.2.2)
Если
в
силу
того,
что
на
момент
заключения
страхового
договора
доступна
только
информация
о
достигнутом
возрасте
х,
или
по
каким-либо
другим
причинам
для
мо
делирования
распределения
продолжительности
предстоящей
жизни
используется
агрегативная
таблица
смертности,
то
условное
распределение
С.в.
Т(х)
- t
совпадает
с
распределением
С.в.
Т(х
+t)
и
равенство
(7.2.2)
можно
переписать
в
виде
iV(A
x
)
=A
x
+
t
- P(Ax)ax+t.
(7.2.3)
Формулы
(7.2.2)
и
(7.2.3)
показывают,
что
(Нетто-резерв)
=
(актуарная
настоящая
стоимость
бессрочного
страхования
на
случай
смерти
для
лица
в
возрасте
х
+t
лет)
-
(актуарная
настоящая
стоимость
будущих
нетто-премий,
выплачиваемых
с
интенсивностью
Р(А
х
)
в
год).
Выражения
для
Р(А
х
)
и
tV(Ax)
связаны
между
собой.
Если
t =
О,
формула
(7.2.3)
дает
oV(A
x
) =
О.
Это
-
следствие
применения
принципа
эквивалентности
в
момент
заключения
договора.
Замечания
об
обозначениях.
В
этой
книге
мы
будем
упрощать
вид
формул
за
счет
исключения
обозначений,
связанных
с
селекцией,
кроме
тех
случаев,
когда
их
использование
является
необходимым
или
полезным
в
конкретных
ситуациях.
При
рассмотрении
нетто-резервов
мы
будем
использовать
символ
J..Lx(t)
для
обозна
чения
интенсивности
смертности,
чтобы
подчеркнуть,
что
условные
распределения,
используемые
при
расчете
резервов,
получены
из
распределения
с.в.
Т(х).
Нетто-резерв
определен
в
разд.
7.1
как
условное
математическое
ожидание
слу
чайной
величины
потерь.
В
этом
разделе
при
нахождении
выражений
для
таких
условных
математических
ожиданий
использовалось
распределение
с.в.
Т(х)
-t
при
условии
Т(х)
> t
и
такая
же
процентная
ставка
и
такое
же
распределение
С.в.
Т(х),
как и
при
определении
нетто-премий
согласно
принципу
эквивалентности
в
момент
времени
t =
О.
Новым
в
расчетах
математического
ожидания
являлось
только
ис
пользование
информации
о
дожитии
лица
(х)
до
момента
времени
t.
Исчерпываю
щий
принцип
расчета резервов
потребовал
бы
учета
всей
новой
информации,
касаю
щейся
случайных
величин
потерь
и
их
распределений,
чтобы
оценить
обязательства,
относящиеся
к
моменту
времени,
для
которого
рассчитывается
резерв.
В
гл.
7
и
8

7.2.
Нетто-резервы
в
непрерывной
модели
193
«процесс
обучения»
на
основе
накапливающихся
наблюдений,
состоящий
в
моди
фикации
предположений,
при
которых
оценивается
нетто-резерв,
исследоваться
не
будет.
По
аналогии
с
тем,
как
мы
выводили
формулу
(6.2.6),
можно
определить
дис
персию
С.в.
tL
следующим
образом:
а
значит,
L
= T(x)-t
[1
Р(А
х
)]
_
Р(А
х
)
t V + 8 б'
- - 2
D[,L
I
Т(х)
>
t]
=
[1
+
РС:х)]
D[vT(x)-t
I
Т(х)
>
t]
- - 2
[
Р(Ах)]
2 - - 2
= 1 +
б
[ A
x
+
t
- (A
x
+
t
) ].
(7.2.4)
(7.2.5)
Отметим
связь
с
формулой
(6.2.6)
и
тот
факт,
что
этот
результат
справедлив
ДЛЯ
всех
величин
премиЙ.
Он
не
зависит
от
принципа
эквивалентности.
Пример
7.2.1.
Продолжая
пример
6.2.1,
ВЫЧИСЛИМ
iV(A
x
)
и
D[tLIT(x)
>t].
Решение.
Так
как
Ах,
ах
и
Р(А
х
)
не
зависят
от
возраста
х,
формула
(7.2.3)
приобретает
вид
tv(Ax)
=
Ах
-
Р(Ах)а
х
=
О,
t
~
О.
в
этом
случае
будущие
премии
уже
эквивалентны
будущим
страховым
выплатам,
и не
требуется
никакого
резерва.
Кроме
того,
в
этом
случае
формула
(7.2.5)
сводится
к
равенству
- - 2
D[,L
I
Т(х)
>
t]
=
[1+
РС:х)]
[2А
х
-
(Ах
)2]
=
D[L]
=0,25,
как
и
в
примере
6.2.1.
Здесь
дисперсия
С.в.
tL
не
зависит
ни
от
возраста
х,
ни
от
периода
t.
...
Пример
7.2.2.
Пусть
смертность
подчиняется
закону
Муавра,
причем
lх
=
100
-
х,
а
процентная
ставка
составляет
6%.
Подсчитаем
(а)
Р(А
з5
),
(Ь)
tv(А
з5
)
и
D[tL
I
Т(х)
>
t]
при
t =
0,10,20,
...
,60.
Решение.
(а)
Так
как
lх
=
100-х,
то
tРЗ5
=
1-t/65
и
tРЗ5р(35+t)
=
1/65
для
О
~
t < 65.
Отсюда
следует,
что
А
=
(65
v
t
.!:..-
dt =
а6510,О6
=
О
258047
35
Jo
65 65
' .
Таким
образом,
~
-
БА
З5
Р(А
з5
)
=
А
=0,020266.
1-
35
(Ь)
В
возрасте
35
+t
имеем
А
з5
+
t
= a
65
_
t
l/(65 - t)
и
- - - 1 -
А
з5
+
t
t
V
(А
з5
)
=
А
з5
+
t
- 0,020266 ln(1,o6)
Далее,
1
65
-
t
1
2-
2
А
= v
2
'U
du
=
a65=t1
35+t
о
65
- t
65
- t
7 _ 11<'\'\

194
Гл.
7.
Нетто-резервы
и
в
силу
равенства
(7.2.5)·
2
]
[
0,020266]
[2
- -
2]
D[t
L
I
Т(х)
>t = 1 + In(1,06)
А
з5
+
t
-
(А
з5
+
t
)
.
При
меняя
эту
формулу,
мы
получим
следующие
результаты:
t
iV(А
з5
)
о
0,0000
10
0,0557
20
0,1289
30
0,2271
40
0,3619
50
0,5508
60
0,8214
D[tLI
Т(35)
>
t]
0,1187
0,1201
0,1173
0,1073
0,0861
0,0508
0,0097
(7.2.7)
Заметим,
что
D[tL I
Т(35)
>
t]
сходится
к нулю.
Это
-
следствие
того,
что
ситу-
ация
становится
более
определенной.
"
В
таблице
из
примера
7.2.2
вычисляются
математическое
ожидание
и
дисперсия
условных
распределений
С.в.
tL
для
некоторых
значений
t.
Для
более
глубокого
понимания
природы
резервов
исследуем
эти
распределения
подробнее.
Ранее
мы
исследовали
случай
t =
О
в
равенстве
(6.2.11),
следующем
за
примером
6.2.3.
Из
формулы
(7.2.1)
вытекает,
что
_ _ _ _
L
-
Т(ж)-t
_
Р-
(А-
)-
-
Т(ж)-t
[6
+
Р(А
х
)]
_
Р(А
х
)
(7 2
6)
t - V
ж
aT(x)-tl - v 6
6'
..
Если
6 >
О,
то
tL
является
убывающей
функцией
от
Т
(х)
- t
и
удовлетворяет
условию
Используя
рис.
6.2.1
в
качестве
руководства,
можно
последовательно
повторить
шаги
вывода
формулы
(6.2.11),
чтобы
установить
следующее
соотношение
между
РТ(х)(U)
и
функцией
распределения
С.в.
tL
при
условии
Т(х)
>
t,
которую
мы
обо
значим
FtL(Y).
Для
некоторого
значения
У из
интервала,
указанного
в
(7.2.7),
имеем
FtL(y) =
Р[
tL
~
у
I
Т(х)
>
t]
=
Р
[vT(Z)-t
[д
+
~(Ax)]
_
Р(:х)
~
у
Т(х)
>
t]
=
Р
[vT(X)-t
~
6у
+
Р(А
х
)
Т(х)
>
t]
~
6+
Р(А
х
)
[
1
[!5
У
+
Р
(Ах)
] ]
=
Р
Т
(х)
~
t - 6ln 6 +
Р(
Ах)
Т
(х)
> t
_
Р[Т(х)
~
t - (1/8){ln[!5y +
Р(А
х
)]/[!5
+
Р(А
х
)])]
[
()
] (7.2.8)
РТ
х
>t
1 -
Fт(ж)[t
- (1/6)
ln{[!5y
+
Р(А
ж
)]/[6
+
Р(А
х
)]}]
( ) (7.2.9)
1 -
РТ(х}
t
Дифференцирование
этой
формулы
по
У
дает
функцию
плотности
С.в.
tL
при
усло-
вии
Т
(х)
>
t:
_ _
1 ( 1
[6
У
+Р(Ах)])
ftL(Y) =
[!5у
+
Р(А
х
)][l
_
РТ(х)
(t)] fT(x) 1 -
б
ln 6+
Р(А
ж
)'
(7.2.10)

7.2.
Нетто-резервы
в
непрерывной
модели
195
Для
агрегативной
модели
смертности
условное
распределение
С.в.
Т{х)
- t
при
усло
вии
Т{х)
> t
совпадает
с
распределением
С.в.
Т(х
+t),
так
что
формулы
(7.2.8),
(7.2.9)
и
(7.2.10)
сводятся соответственно
к
равенствам
(7.2.11)
(7.2.12)
(7.2.13)
Для
иллюстрации
этих
понятий
продолжим
при
мер
7.2.2.
Пример
7.2.3.
Для
страхового
договора
и
для
предположений
из
примера
7.2.2
(а)
выведем
выражения
для
функции
распределения
и
функции
плотности
С.в.
tL
при
условии
Т(х)
> t.
(Ь)
нарисуем
графики
этих
условных
функций
плотности
при
t =
0,20,40
и
60.
Решение.
(а)
Поскольку
в
при
мере
7.2.2
использована
агрегативная
модель
смертности,
воспользуемся
формулами
(7.2.12)
и
(7.2.13).
В
при
мере
7.2.2
{
U/(65 -
t)
F
Т
(З5+t){U)
= 1
{
1/(65
- t)
fТ(З5+t)
(и)
=
О
при
О
~
u
~
65 - t,
при
65 - t <
и,
при
О
~
u
~
65 - t,
в
остальных
случаях.
О
~
у
~
1.
Рис.
7.2.1
является
модификацией
рис.
6.2.1
для
этого
примера.
На
этом
рисунке
область
значений
С.в.
Т(35
+ t)
расположена
на
оси
и,
а
область
значений
С.в.
tL -
на
оси
у.
Соотношение
между
исходами
случайных
величин
Т(35
+ t)
и
tL
задается
функцией
потерь
у
= lt
(и)
и
указывается
пунктирными
линиями,
соединяющими
на
рисунке
значения
и
и
у.
Область
определения
функции
плотности
fТ(З5+t){U)
лежит
на
оси
и,
а
область
значений
-
на
оси
у.
Область
определения
функции
плотности
ft
L
(у)
расположена
на
оси
у,
а
область
ее
значений
можно
представлять
себе
лежа
щей
на
оси,
перпендикулярной
плоскости
(u,у),
но
для
простоты
она
изображена
прямой,
перпендикулярной
оси
у,
на
плоскости
(и,
у)
.
Для
определения
функции
распределения
С.в.
tL
начнем
со
значения
у,
соот
ветствующего
значению
и
из
интервала
(О,
65-t).
Для
таких
значений
у,
согласно
(7.2.12) ,
F ( ) = 1 _
(-1/8)
ln{[8y +
Р(.А
з5
)]/[8
+
Р(.А
з5
)Р(.А
з5
)]}
t
L
У
65 - t '
Если
у
> 1,
то
FtL
= 1.
Далее,
для
значений
у,
соответствующих
значениям
и
из
интервала
(О,
65-t),
согласно
формуле
(7.2.13),
Р(.А
з5
)
- 6
~
У
~
1,
в
остальных
случаях
.
.,.
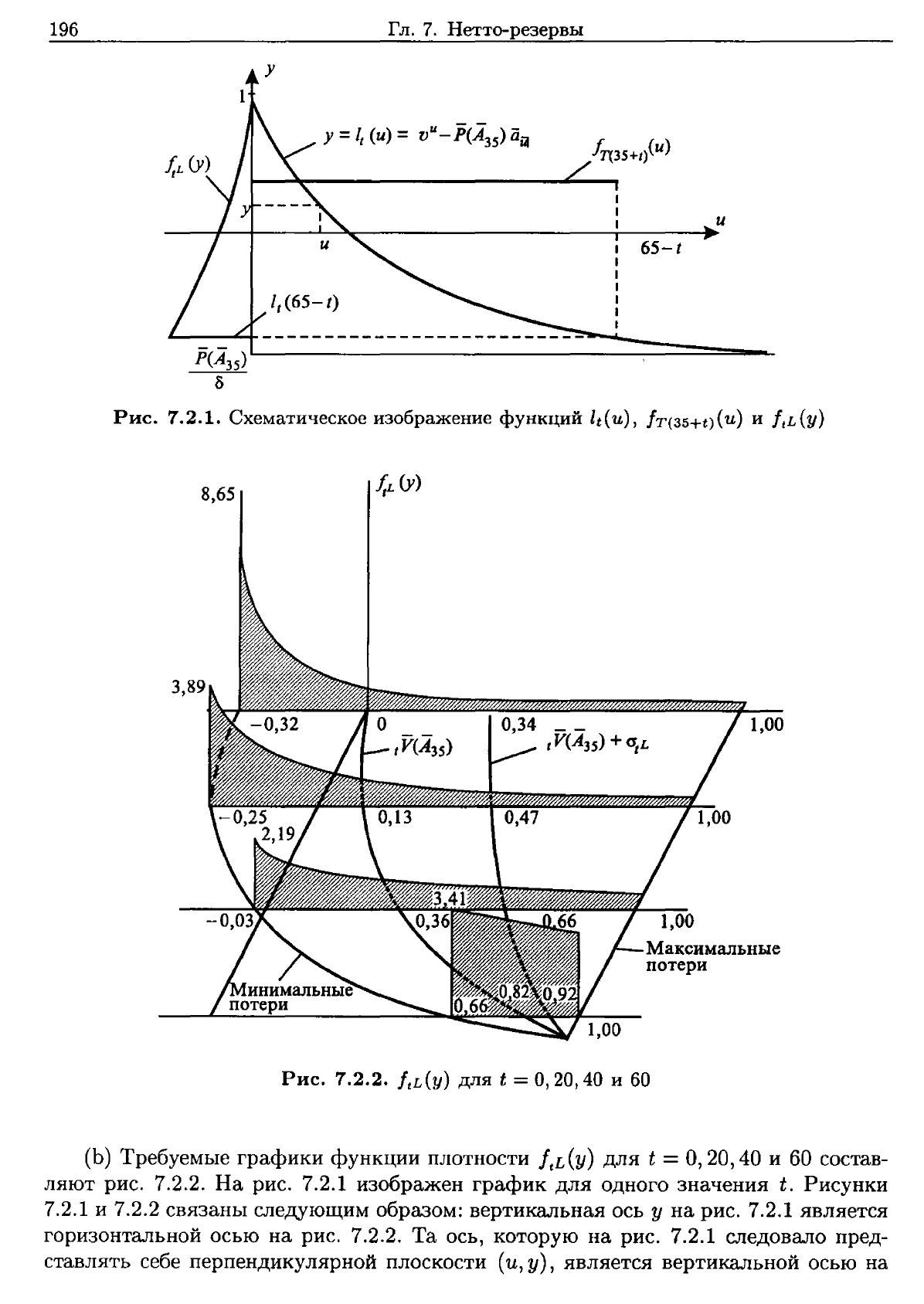
196
Гл.
7.
Нетто-резервы
у
u
65-t
Р(А
з5
)с.:==========..::==::::=========-
о
Рис.
7.2.1.
Схематическое
изображение
функций
lt(u),
fТ(З5+t)(U)
и
ftL(Y)
1,00
Максимальные
потери
8,65
3,89
0,34
__
t
V(А
зs
)
+
<J,L
0,47
1,00
Рис.
7.2.2.
ftL(Y)
для
t =
0,20,40
и
60
(Ь)
Требуемые
графики
функции
плотности
ftL(Y)
для
t =
0,20,40
и
60
состав
ляют
рис.
7.2.2.
На
рис.
7.2.1
изображен
график
для
одного
значения
t.
Рисунки
7.2.1
и
7.2.2
связаны
следующим
образом:
вертикальная
ось
у
на
рис.
7.2.1
является
горизонтальной
осью
на
рис.
7.2.2.
Та
ось,
которую
на
рис.
7.2.1
следовало
пред
ставлять
себе
перпендикулярной
плоскости
(и,
у),
является
вертикальной
осью
на

7.3.
Другие
формулы
для
нетто-резервов
в
непрерывной
модели
197
рис.
7.2.2.
Обратите
внимание
на
кривые
на
плоскости
(у,
t),
обозначающие
мини
мальные
и
максимальные
возможные
потери,
ожидаемые
потери
(нетто-резерв)
и
ожидаемые
потери
плюс
стандартное
отклонение
потерь.
•
Таблице
6.2.1
соответствует
табл.
7.2.1
для
нетто-резервов.
Мы
не
включаем
в
нее
случайной
величины
будущих
потерь
tL
и
явных
формул
для
D[tLIT(x)
>t],
соответствующих
различным
нетто-резервам.
Таблица
7.2.1.
Нетто-резервы
в
непрерывноii
модели
для
возраста
на
момент
заключения
договора
х,
момента
t
и
страховой
суммы
размера
1
Вид
страхового
покры
тия
Междуна
родное
актуарное
обозначение
Формула
расчета
по
перспективному
методу
t
~
n,
t > n
t
~
h <
n,
h < t <
n,
t=n
t <
n,
t=n
A
x
+
t
-
P(Ax)ax+t
{
.Ax~t:n-tl
-
Р(.А~:rn)liх+t:n-tl'
t < n,
О,
t = n
{
.Ax+t:n-tl -
P(.Ax:rn)iix+t:n-tl' t <
n,
1,
t = n
{
--!x+t
- hP(Ax)ax+t:h-tl, t
~
h,
A
x
+
t
,
t>
h
{
~x+t:n-tl
- h.P(.Ax:rn)iix+t:h_tl,
Ax+t:n-tl'
1,
{
.Ax+t:n~tl-
P(.Ax:,\,)lix+t:n-t!'
1,
{
:-t1ё.iХ+t
-
P(nllix)ё.ix+t:n-tl,
ax+t,
h - -
t
V(Ах:nд
Бессрочное
страхование
на
случай
смерти
Страхование
на
случай
смерти
на
срок
n
лет
Страхование
на
дожи
тие
на
срок
n
лет
Смешанное
страхование
на
срок
n
лет
Бессрочное
страхование
на
случай
смерти
с
h-летним
сроком
выпла
ты
премий
Смешанное
страхование
на
срок
n
лет
с
h-летним
сроком
выплаты
премий
Бессрочный
страховой
аннуитет,
отсроченный
на
n
лет
7.3.
Другие
формулы
для
нетто-резервов
в
непрерывной
модели
До
сих
пор
нетто-резерв
определялся
как
условное
математическое
ожидание
случайной
величины
будущих
потерь
и
рассматривался
лишь
один
метод
выраже
ния
формул
для
резервов
в
непрерывной
модели,
а
именно
nерсnе'Х:ти6'Н,'Ый,
согласно
которому
нетто-резерв
является
разностью
между
актуарными
настоящими
стоимо
стями
будущих
выплат
и
будущих
hetto-премиЙ.
На
основе
перспективного
метода
мы
можем
легко
вывести
другие
три
общие
формулы
для
договоров
с
постоянными
размерами
страховых
выплат
и
hetto-премиЙ.
Мы
приведем
их
для
случая
смешан
ного
страхования
на
срок
n
лет.
Фор.мула
разности
nре.миЙ
для
tV(.4x:nJ)
получается
из
перспективной
формулы
ДЛЯ
tV(.4x:nJ)
вынесением
за
скобки
ax+t:n-tl:
iV
(.4
Х
:
nl
)
=
[~x+t:п=tl_
Р(Ах:nд]
ax+t:n-tl = [P(Ax+t:n-tl) - P(Ax:nl)]iix+t:n-tl'
(7.3.1)
ax+t:n-tl

198
Гл.
7.
Нетто-резервы
(7.3.2)
Формула
(7.3.1)
выражает
нетто-резерв
как
актуарную
настоящую
стоимость
раз
ности
премий,
выплачиваемой
в
течение
оставшегося
срока
выплаты.
Эта
разность
получается
путем
вычитания
исходной
ежегодной
нетто-премии
из
нетто-премии
по
договору
страхования,
заключенному
с
лицом
(х
+t)
с
теми
же
выплатами.
Вторая
формула
получается
вынесением
за
скобки
в
перспективной
формуле
актуарной
настоящей
стоимости
будущих
страховых
выплат.
Таким
образом,
- -
[-
- ax+t:n=tl] -
[Р(Ах:nд
]-
tV(A
x
:
m
)
= 1 -
Р(А
х
:
m
)
А
Ax+t:n-tl = 1 -
Р(А
) Ax+t:n-tl'
x+t:n-tl x+t:n-tl
Она
выражает
нетто-резерв
как
актуарную
настоящую
стоимость той
части
предсто
ящих
страховых
выплат,
которая
не
покрывается
будущими
нетто-премиями,
кото
рые
еще
предстоит
собрать.
Заметим,
что
P(Ax+t:n-tl) -
нетто-премия
в
ситуации,
когда
будущие
выплаты
покрываются
только
за счет
премий,
которые
будут
собра
ны,
а
P(A:t:rn)
является
фактически
выплачиваемой
hetto-премиеЙ.
Таким
образом,
P(A
x
:
rn
)/
P(Ax+t:n-tl)
является
частью
будущих
страховых
выплат,
покрываемой
бу
дущими
нетто-премиями.
Эта
формула
называется
формулой
оnлшчен:ноiJ.
страховой
суммы
по
аналогии
с
обсуждаемым
в
гл.
16
страховым
покрытием,
обеспеченным
сохраненными
выплатами.
Формулы,
аналогичные
формулам
(7.3.1)
и
(7.3.2),
суще
ствуют
для
многих
видов
нетто-резервов.
Третьим
выражением
является
ретроспективная
формула.
Мы
выведем
ее
из
более
общего
соотношения.
Из
упр.
4.12
и
из
формул
(5.2.18)
и
(5.2.19)
для
t < n - s
имеем
- - 1 -
Ax+s:n-sl = A
x
+
s
:
tl
+ tEx+s Ax+s+t:n-s-tl'
а
х
+
а
:
n
-
а
!
=
ах+а:ll
+ tEx+s ax+s+t:n-s-tl'
Подставляя
эти
выражения
в
перспективную
формулу
для
s
V(J1
x
:
rn
),
получим
--
-1
--
-
s
V(A
x
:
rn
) = A
x
+
s
:
tl
- P(Ax:rn)ax+s:tl
+tEx+s [Ax+s+t:n-t-sl - P(Ax:rn)ax+s+t:n-t-sIJ
-1
--
---
=A
x
+
s
:
tl
+tEx+s
s+t
V(A
x
:
m
)
-
P(Ax:Тil)ax+s:tl·
(7.3.3)
Таким
образом,
нетто-резервы
в
начале
и
в
конце
интервала
длины
t
лет
связыва
ются
следующим
соотношением
(нетто-резерв
в
начале
интервала)
=
(актуарная
настоящая
стоимость
в
начале
интервала
страховых
выплат,
которые
производятся
в
течение
этого
интервала)
+
(актуарная
настоящая
стоимость
в
начале
интервала
страховых
выплат
при
страховании
на
дожитие,
равных
нетто-резерву
в
конце
интервала)
-
(актуарная
настоящая
стоимость
нетто-премий,
выплачиваемых
в
течение
интервала).
Это
соотношение,
переписанное
в
виде
s
V(A
x
:
Тil
)
+
P(A
x
:
ffi
)a:t+s:n-tl = A
x
+
s
:
tl
+ tEx+s
s+t
V(A
x
:
rn
),
(7.3.4)
показывает,
что
актуарные
настоящие
стоимости
финансовых
ресурсов
и
обяза
тельств
страховщика
равны.

7.3.
Другие
формулы
для
нетто-резервов
в
непрерывной
модели
199
Ретроспективная
формула
получается
из
формулы
(7.3.4),
если
положить
s =
О,
заметить,
что,
согласно
принципу
эквивалентности,
01l(A
x
:
nl
) =
О,
и
разрешить
по
лученное
равенство
относительно
iV
(A
x
:
nl
).
Таким
образом,
- - 1 - - _
-1
tV(A
x
:
nl
) =
-Е
[P(Ax:nl)ax:tl -
А
х
:
л
]·
t
х
Далее,
ВХ:п
=
ах:п/
tEx,
так
что
эта
формула
сводится
к
равенству
iV
(.4
х
:
m
)
=
P(.4
x
:
nl
)sx:tl
- tkx.
(7.3.5)
Здесь
-
-1
tkx =
А
х
:
п
/tEx
называется
'н,а'к;оnле'Н,'Н,оu
стоuмостью
страхова'Н,uя.
Заметим,
что
tkx =
(t
v
S
sPx
~x(B)
ds =
{t
(1
+
i)t-
s
l
x
+
8
I-lх(в)
ds .
10
v
tPx
10
lx+t
(7.3.6)
(7.3.7)
(7.3.8)
Это
можно
интерпретировать
как
разложенную
на
каждое
из
lx+t
доживших
лиц
сумму
выплат
на
случай
смерти
в
совокупности
дожития
между
возрастами
х
и
х
+ t
лет.
Таким
образом,
резерв
можно
рассматривать
как
разность
между
нетто
премиями,
накопленными
с
учетом
процента и
распределенными
лишь
среди
дожив
ших
до
возраста
х
+ t,
и
накопленной
стоимостью
страхования.
Мы
заключаем
этот
раздел
некоторыми
специальными
формулами,
выражаю
щими
нетто-резерв
по
договору
бессрочного
страхования
на
случай
смерти
в
тер
минах
одной
актуарной
функции.
Аналогичные
формулы
имеют
место
для
нетто
резервов
по
договору
смешанного
страхования
на
срок
n
лет,
если
нетто-премии
выплачиваются
непрерывно
в
течение
n
лет.
Так
как
мы
использовали
формулу
(5.2.8),
чтобы
выразить
Р(А
х
)
в
терминах
8
и
ах
или
Ах,
мы
можем
воспользо
ваться
теми
же
соображениями,
чтобы
выразить
t1l(;1x)
в
терминах
одной
из
таких
актуарных
функций
ах,
Ах,
Р(А
х
)
и
величины
б.
Чтобы
выразить
нетто-резерв
через
актуарную
функцию
для
аннуитетов,
под
ставим
(6.2.9)
и
(5.2.8)
в
перспективную
формулу
(7.2.3)
и
получим
- - _ ( 1 ) _
o,x+t
tV(Ax) = 1 -
бах+t
-
::-
- 8 ax+t = 1 -
-_-.
ах ах
Далее,
подставив
(6.2.9)
в
формулу
разности
премий,
получим
- - - - - - _ P(A
x
+
t
)
-
Р(А
х
)
tV(A
x) = [P(Ax+t ) - P(Ax))ax+t =
(А)
д
.
Р
x+t
+
(7.3.9)
(7.3.10)
Наконец,
можно
переписать
формулу
(7.3.8),
используя
равенство
A
x
+
t
=
1-
8a
x
+t,
и
получить
1I(A
) = 1 _ 1 - A
x
+
t
= A
x
+
t
-
Ах
t
х
1 -
Ах
1 -
Ах
.
При
выводе
трех
последних
формул
использовалось
соотношение
(5.2.8),
связы
вающее
аннуитет
в
период
выплаты
премий
и
страховые
обязательства
в
течение
срока
страхования.
Таким
образом,
эти
формулы
годятся
только
для
бессрочного
страхования
на
случай
смерти
и
бессрочного
смешанного
страхования,
для
которых
период
выплаты
премий
совпадает
со
сроком
страхования.
Кроме
того,
частота
вы-

200
Гл.
7.
Нетто-резервы
платы
премий
должна
совпадать
с
«частотой»
страховых
выплат.
Мы
увидим,
что
премии
с
корректирующим
платежом
некоторым
специальным
образом
у
довлетво
ряют
этим
требованиям.
Замечание.
Хотя
в
большинстве
приложений
нетто-резервы
неотрицательны,
не
существует
математических
теорем,
гарантирующих
это
свойство.
На
самом
деле
читатель
может
объединить
упр.
4.2
и
формулу
(7.3.10),
чтобы
быстро
убедиться,
что
отрицательные
нетто-резервы
действительно
возможны.
7.4.
Нетто-резервы
в
дискретной
модели
Обсуждаемые
в
этом
разделе
нетто-резервы
относятся
к
видам
страхования
из
разд.
6.3
с
ежегодной
выплатой
премии
и
страховой
выплатой
в
конце
года
смерти.
Как
и
в
разд.
7.2,
можно
предполагать,
что
смертность
описывается
агрегативной
или
селекционной
таблицей.
Мы
будем
выводить
формулы
для
агрегативного
слу
чая,
в
котором
обозначения
проще.
Рассмотрим
бессрочное
страхование
лица
(х)
на случай
смерти
с
выплатой
размера
1
и
нетто-премией
Р
х
'
Следуя
изложению
разд.
7.2,
определим
нетто-резерв
kVx
для
страхователя,
прожившего
k
лет
с
момен
та
заключения
договора,
как
условное
математическое
ожидание
будущих
потерь
kL
в
момент
времени
k.
Более
точно,
L
-
[K(x)-k]+l
р"
k - V -
х
а.-::[
к:-:-('-х7"")
--k:-;"]
-+~ll'
kV
x
=E[k L IК
(х)
=k, k +
1,
...
].
Перспективная
формула
для
нетто-резерва
имеет
вид
kVx
= A
x
+
k
-
Р
х
ax+k'
(7.4.1)
(7.4.2)
(7.4.3)
Как
и
в
разд.
7.2,
эта
формула
является
разностью
между
актуарной
настоящей
сто
имостью
будущих
страховых
выплат
и
актуарной
настоящей
стоимостью
будущих
hetto-премиЙ.
По
аналогии
с
формулой
(7.2.4)
имеем
D[kLIK(x)=k,
k +
1,
...
] =D
[V[K(XJ-k]+l
(1 +
i)
К(х)
=
k,k
+
1,
]
(1
+ i )2
D[v[K(zJ-k]+l1
К(х)
= k, k +
1,
]
-
(1
+ i )2
["А
хн
-
(А
хн
)2].
(7.4.4)
Пример
7.4.1.
В
продолжение
примера
6.3.1
рассчитаем
kVx
и
D[kL I
К(х)=
k,
k+1,
...
].
Решение.
Здесь
Ах,
ах
и
Р
х
не
зависят
от
возраста
х,
так
что
A
x
+
k
=
Ах
и
k=0,1,2,
....
Кроме
того,
из
формулы
(7.4.4)
также
следует,
что
D[kL I
К(х)
= k, k + 1,
...
]
D[L] = 0,2347. •
Формулы
нетто-резервов,
сведенные
в
табл.
7.4.1,
соответствуют
нетто-премиям
из
табл.
6.3.1
и
аналогичны
формулам
нетто-резервов
из
табл.
7.2.1.
