Бауэрс Н., Гербер Х., Джанс Д., Несбитт С., Хикман Дж. Актуарная математика
Подождите немного. Документ загружается.


6.1.
Введение
161
(6.1.1)
(с)
Принцип
III. Р
является
такой
ежегодной
премией,
что
страховщику,
приме
няющему функцию
полезности
u(х)
=
_е-О,lх,
будет
безразлично,
принять
или
не
принять
соответствующий
риск
на
страхование.
Для
каждого
ИЗ
этих
трех
случаев
мы
будем
предполагать,
что
страховщик
работает
с
эффективной
годовой
процентной
ставкой
i = 0,06.
Решение.
Для
К
= k
и
для
произвольной
премии
Р
настоящая
стоимость
финансовых
потерь
на
момент
заключения
договора
равна
l(k)
= V
k
+
1
-
Pa
k
+
1
1=
(1
+
p/d)vk+l
-
P/d,
k =
0,1,2,3,4.
Соответствующая
случайная
величина
потерь
L
-
К+l
Р"
-
это
- V -
а
к
+lI'
(а)
Поскольку
l(k)
убывает
с
ростом
k,
требование
принципа
1
будет
выпол
няться,
если
премия
Р
такова,
что
v
2
-
Ра
21
=
О.
в
этом
случае
финансовые
потери
положительны
только
при
К
=
О,
что
имеет
вероятность
0,2 < 0,25.
Таким
образом,
для
этого
принципа
Р
=
1/821
= 0,45796.
(Ь)
Следуя
формуле
(1.3.6),
мы
ищем
премию
Р,
такую,
что
u(w) =
E[u(w-L)).
Согласно
принципу
П,
u(х)
=
Х,
и
мы
имеем
w = E[w -
L)
= w - E[LJ.
Таким
образом,
принцип
II
эквивалентен
следующему
требованию:
премия
Р
должна
вы
бираться
так,
чтобы
выолнялосьь
равенство
E[L] =
О.
в
рассматриваемом
примере
мы
требуем,
чтобы
4
L(V
k
+
1
-
Pa
k
+
1
1)
Р(К
=
k)
=
О,
k=O
откуда
вытекает,
что
Р
=0,30272.
(с)
Снова
используя
формулу
(1.3.6)
и
функцию
полезности
из
принципа
III,
получаем
_e-
O
,lw
=
E[_e-
O
,l(w-L)]
=
_e-
О
,
lW
Е[е
О
,lL].
Таким
образом,
принцип
III
эквивалентен
следующему
требованию:
премия
Р
долж
на
выбираться
так,
чтобы
E[eO,lLJ
= 1.
В
рассматриваемом
примере
мы
требуем,
чтобы
4
L exp[0,1(v
k
+
1
-
Pii
k
+
11
)]
Р(К
=k) =
1,
k=O
откуда
вытекает,
что
Р =0,30628.
Эти
результаты
сведены
в
следующей
таблице:
Настоящая
СТОИМОСТЬ
финансо
вых
потерь,
если
премии
рассчи
тываются
согласно
принципу
(6.1.2)
k
о
1
2
3
4
Вероятность
k I
qo
0,2
0,2
0,2
0,2
0,2
Премия
Общая
формула
1
Р"
v -
ал
2
Р"
v -
a21
3
Р"
v -
аЗJ
4
Р"
v -
a41
5
Р"
v -
аы
1
П
III
0,48544 0,64067 0,63712
О
0,30169 0,29477
-0,45796
-0,01811
-0,02819
-0,89000
-0,31981
-0,33287
-1,29758
-0,60443
-0,62031
0,45796 0,30272 0,30628
III
1,06579
1,02992
0,99718
0,96726
0,93985
Математическое
ожидание
6 -
1855
-0,43202
0,00000
-0,12020
1,00000

162
Гл.
6.
Нетто-премии
Эта
таблица
показывает,
что
в
данном
при
мере
лица,
принимающие
решения
на
основе
принципов
1
и
III,
уменьшают
свой
риск
в
том
смысле,
что
они
требуют
отрицательности математического
ожидания
настоящей
стоимости
потерь.
Т
Премии,
определяемые
согласно
принципу
1,
мы
будем
называть
nерсен,mu.л:ь
н,'ым.и
nрем.uям,u.
Хотя
этот
принцип
на
первый
взгляд
выглядит
привлекательно,
легко
показать,
что
его
использование
может
привести к
весьма
неудовлетворитель
ным
премиям.
Такие
случаи
рассматриваются
в
примере
6.2.3.
Принцип
II
имеет
много
практических
применениЙ.
Для
формального
изложе
ния
определим
потери
страховщика
L
как
случайную
величину,
равную
настоящей
стоимости
выплат,
которые
должен
произвести
страховщик,
минус
аннуитет
пре
мий,
которые
должен
выплатить
страхователь.
Принцип
II
называется
nрин,'Циnо.м.
Э7Свuваленmносmu,
и
определяющее
его
требование
состоит
в
том,
чтобы
E[L] =
О.
(6.1.3)
Мы
будем
называть
премии,
удовлетворяющие
условию
(6.1.3),
неmmо-nрем,uям,u
1
).
Их
можно
также
определить
условием
Е[настоящая
стоимость
страховых
выплат]
=
Е[настоящая
стоимость
hetto-премиЙ].
С
помощью
методов,
разработанных
в
гл.
4
и
5
для
расчета
таких
актуарных
настоящих
стоимостей,
это
уравнение
можно
привести
к
виду,
который
допускает
решение
относительно
премиЙ.
Скажем,
в
примере
6.1.1,
в
котором
нетто-премии
постоянны
и
выплаты
имеют
величину
1,
уравнение
(6.1.1)
можно
записать
в
виде
А
о
=
Рао
и
получить
для
ао
выражение
2::=0
v
k
kPo,
Когда
принцип
эквивалент
ности
при
меняется
для
определения
величины
единовременной
премии
в
момент
заключения
договора
страхования
жизни
или
страхового
аннуитета,
эта
премия
приравнивается
к
актуарной
настоящей
стоимости
страховых
выплат
и
называется
едuноврем.енноЙ
нетто-nрем.иеЙ.
Премии,
расчет
которых
основан
на
принципе
III
с
показательной
функцией
по
лезности,
называются
nоказательны.мu
nре.мuя.мu.
Такие
премии
являются
непро
порциональными
в
том
смысле,
что
премии
по
договору
с
выплатой
размера
10
единиц
более,
чем
в
10
раз,
превосходят
премии
по
договору
с
выплатой
размера
1
(см.
упр.
6.2).
Это
согласуется
с
функциями
полезности
лиц,
не
склонных
к
риску.
6.2.
Непрерывная
модель
Основные
понятия,
используемые
при
определении
премий
на
основе
принципа
эквивалентности,
мы
проиллюстрируем
сначала
на
примере
непрерывной
выпла
ты
постоянных
годовых
премий
при
бессрочном
страховании
на
случай
смерти
с
l)в
оригинале
«benefit premium•.
В
переводе
мы
используем
термин
«нетто-премия.
(и
в
дальнейшем
«нетто-резерв.),
поскольку
расчет
этой
премии
в
рассматриваемой
модели
основан
на
выплатах
без
учета
расходов
страховщика,
описанных
в
гл.
15.
Следуя
этой
логике,
«нетто
премиями.
могут
называться
и
другие,
например
персентильные,
премии,
но
мы
резервируем
этот
термин
за
премиями,
рассчитанными
на
основе
принципа
эквивалентности,
так как
в
дальнейшем
в
основном
рассматриваются
именно
они.
Обращаем
внимание
читателя
на
следующие
два
момента:
во-первых,
в
гл.
1,
разд.
1.3
(и
только
там),
уже
встречался
термин
«нетто-премия.
(в
оригинале
«net
premium.
и
«рше
premium.),
пони
маемый
в
несколько
ином
смысле,
что
не
приведет
к
недора
зумениям;
во-вторых,
экономист
не
должен
воспринимать
введенный
здесь
термин
как
привычный
ему
термин
из
бухгалтерского
учета.
-
Прuм.
ред.

6.2.
Непрерывная
модель
163
выплатой
суммы
размера
1
в
момент
смерти
l
)
лица
(х).
Для
любой
непрерывно
выплачиваемой
премии
Р
рассмотрим
t
--
l(t) = v -
Рап,
(6.2.1)
настоящую
стоимость
потерь
страховщика,
если
смерть
произошла
в
момент
време
ни
t.
Заметим,
что
1(t)
является
убывающей
функцией
аргумента
t
(фу'Н~'Цuей
по
терь),
для
которой
1
(О)
= 1,
и
l(t)
стремится
к
-
Р
/
д
при
t
-+
00.
Если
to
является
моментом,
когда
l(to) =
О,
то
смерть
до
момента
to
приводит
к
положительным
по
терям,
а
смерть
после
момента
to
-
к
отрицательным
потерям,
т.
е.
к
прибыли.
Эти
соображения
иллюстрируются
на
рис.
6.2.1,
приведенном
далее.
Рассмотрим
случайную
величину
потерь
L =
I(T)
=v
T
-
Рат!,
(6.2.2)
отвечающую
функции
потерь
l(t).
Если
страховщик
определяет
величину
премии,
исходя
из
принципа
эквивалентности,
то
она
обозначается
через
Р(А
х
)
и
удовлетво
ряет
условию
E[L] =
О.
Из
формул
(4.2.6)
и
(5.2.3)
вытекает,
что
Ах
-
Р(А
х
)а
х
=
о,
или
(6.2.3)
Р(А
х
)
=
Ах/ах.
(6.2.4)
Замечание.
В
настоящей
главе
для
упрощения
изложения
мы,
как
правило,
не
пользуемся
селекцией,
а
когда
она
будет
использоваться,
будем
оговаривать
это
специально.
Дисперсию
С.в.
L
можно
использовать
как
меру
изменчивости
величины
потерь
по
отдельному
договору
бессрочного
страхования
на
случай
смерти
вследствие
слу
чайной
природы
продолжительности
предстоящей
жизни.
Когда
E[L] =
О,
D[L]
=
E[L
2
].
ДЛЯ
случайной
величины
потерь
из
формулы
(6.2.2)
имеем
(6.2.5)
D[v
T
-
Рап]
=D
[v
T
-
P(l
~
v
T
)]
=D
[v
T
(1+
~)
-
~]
=D
[v
T
(1
+
~)]
=
D[vT](l+
~)
2 =
РА.
_
(А.)2]
(1+
~)
2 (6.2.6)
Если
премия
определяется
с
помощью
принципа
эквивалентности,
мы
можем
ис
пользовать
формулы
(6.2.4)
и
(5.2.8),
бах
+А
х
= 1,
и
переписать
соотношение
(6.2.6)
в
виде
2А
х
_
(А
х
)2
D[L]
=
(8а
х
)2
(6.2.7)
l)в
дальнейшем,
если
выплаты
премий
производятся
непрерывно,
а
выплаты
на
случай смерти
производится
в
момент
смерти,
то
мы
будем
говорить
о
непрерывной
,модели.
Если
премии
выпла
чиваются
дискретно
(1
раз
в
год,
см.
разд.
6.3,
или
несколько
раз
в
год),
а
выплата
на
случай
смерти
производится
в
конце
года
смерти,
то
мы
говорим
о
диС7Сретной
,модели.
Если
же
премии
выплачиваются
дискретно,
а
выплата
на случай
смерти
производится
в
момент
смерти,
то
мы
говорим
о
nолунеnреРЫ6NОЙ
,модели.
-
При,м.
ред.
6*

164
Гл.
6.
Нетто-премии
,
1
ах
= ,
р+д
и
так
что
Пример
6.2.1.
Вычислим
.Р(А
х
)
и
D[L]
в
предположении,
что
интенсивность
смертности
является
постоянной,
J-L
= 0,04,
а
интенсивность
начисления
процента
д
равна
0,06.
Решение.
В
силу
этих
предположений
ах
= 10,
Ах
= 0,4
и
2А
х
= 0,25.
Приме
няя
формулу
(6.2.4),
получаем
.Р(А
х
)
=
Ах/ах
= 0,04,
и
в
силу
(6.2.7)
D[L] = 0,25 - 0,16 =
О
25
(0,6)2
,.
Учитывая
соотношение
(6.2.7),
мы
можем
рассматривать
числитель
последнего
соотношения
как
дисперсию
потерь
v
T
-
Ах
ПО
договору
бессрочного
страхования
на
случай
смерти
с
единовременной
премиеЙ.
Эта
дисперсия
равна
0,09,
и
потому
стан
дартное
отклонение
величины
потерь
для
страхового
договора
с
такой
непрерывной
выплатой
премий
будет
равно
.j0,25/0,09
=
5/3
от
стандартного
отклонения
вели
чины
потерь
в
случае
единовременной
премии.
Дополнительная
неопределенность
относительно
настоящей
стоимости
премиальных
поступлений
увеличивает
измен
чивость
потерь,
связанную
со
случайной
природой
продолжительности
предстоящей
жизни.
В
примере
6.2.1
.РА
х
= 0,04,
т.
е.
величина
РА
х
равна
постоянной
интенсивно
сти
смертности.
Мы
можем
доказать,
что
это
-
общий
результат,
применяя
сообра
жения
из
примеров
4.2.3
и
5.2.1.
В
предположении,
что
интенсивность
смертности
постоянна,
-
J-L
А
х
=--
/-l+д
- -
J-L(/-l+0)-1
Р(А
х
)
=
(J-L
+ 0)-1 =
{Lj
последняя
величина
не
зависит
от
интенсивности
начисления процента
или
от
воз
раста
в
момент
заключения
договора.
Используя
принцип
эквивалентности
в
форме
соотношения
(6.1.3),
мы
можем
вывести
формулы
для
ежегодных
премий для
целого
ряда
страховых
договоров
в
непрерывной
модели.
Величина
общих
потерь
равна
bTVT
-
ру
= z -
ру,
(6.2.8)
где
• b
t
и
Vt
являются
соответственно
функцией
выплат
и
функцией
дисконтиро
вания,
определенными
перед
формулой
(4.2.1),
•
Р
является
общим
символом
для
годовой
нетто-премии
в
непрерывной
моде
ли,
• у
является
случайной
величиной
настоящей
стоимости
непрерывного
анну
итета,
определенной,
например,
формулой
(5.2.13),
• Z
определяется
формулой
(4.2.2).
Применение
принципа
эквивалентности
приводит
к
равенству
E[bTVT
-
ру]
=
О,
или
Эти
соображения
используются,
премий,
собранные
в
табл.
6.2.1.
.Р
=
E[bTVTJ
Е[У)
.
чтобы
вывести
формулы
для
величины
годовых

6.2.
Непрерывная
модель
165
Интересно
посмотреть,
как
эти
рассуждения
могут
применяться
к
непрерывным
бессрочным
страховым
аннуитетам,
отсроченным
на
n
лет,
с
выплатой
размера
1
в
год.
В
этом
случае
ЬТ
VT
=
О,
Т
~
n,
и
ЬТ
VT
=aT_nl v
n
,
Т
>
n.
Тогда
E[bTvT] =
nРх
E[aT_nlv
n
I
т
>
n]
=v
n
nРх
а
х
+
n
=
Ах:iи
а
х
+
n
.
Однако
на
практике
отсроченные
страховые
аннуитеты
обычно
предусматривают
определенный
тип
выплат
на
случай
смерти,
если
она
произошла
в
период
отсрочки.
Один
такой
договор
рассматривается
в
примере
6.6.2.
Пример
6.2.2.
Выразим
дисперсию
потерь
L,
связанных
со
смешанным
стра
хованием
на
срок
n
лет,
в
терминах
актуарных настоящих
стоимостей
(см.
третью
строчку
в
табл.
6.2.1).
Таблица
6.2.1.
Нетто-премии
в
непрерывной
модели
Компоненты
потерь
Формула
для
премии
Вид
страхового
покрытия
bTVT
РУ,
где
У
есть
Р
= E[bTVT
]/Е(У]
Бессрочное
страхование
на
1v
T
ёiТl
Р(А
х
)
=
~x
случай
смерти
ах
Страхование
на
случай
смерти
1v
T
ёiТl'
Т
~
n
-1
Р(А1.
) =
A
x
:
nт
на
срок
n
лет
О
ёiщ,
Т>
n
X.nТ
-
ax:nl
Смешанное
страхование
на
срок
1v
T
ёiТl'
Т
~
n
- -
A
x
:
nт
n
лет
1v
n
ёiщ,
Т>
n
P(A
x
:
nт
)
=
--
-
ax:nт
Бессрочное
страхование
на
1v
T
ёiТl'
Т
~
h
- -
Ах
случай
смерти
с
h-летним
1v
T
ёihl'
Т>
h
hP(A
x
)
=
--
-
сроком
выплаты
премий
1
}
ах:ю
Смешанное
страхование
на
срок
1v
T
ёiТl'
Т
~
h
- -
..4.
х
;щ
n
лет
с
h-летним
сроком
1v
T
ёihl'
h <
Т
~
n
hP(A
x
:
m
)
=
-_-
выплаты
премий
1v
n
ёihl'
Т>
n
ах:hl
Страхование
на
дожитие
на
О
ёiТl'
Т
~
n
Р(А
.1) =
Ax:k
срок
n
лет
1v
n
ёiщ,
Т>
n
х.т
-
ax:nl
Бессрочный
страховой
аннуитет,
О
ёiТlI
Т
~
n
А
1 -
P(nlax)
=
Z;nТ
а
х
+
n
отсроченный
на
n
лет
2
)
- n
ёiщ,
Т>
n
aT_nlv
ax:nт
Решение.
Используя
обозначение
из
формулы
(4.2.11),
мы
имеем
D[L] = D
[Zз
{1+
P(~X"")
} _
P(~X,iil)]
.
Используя
теперь
формулу
(4.2.10),
мы
получаем
- - 2
[
Р(Ах:щ)]
2 - - 2
D[L]
= 1 +
б
[
А
х
:
т
-
(А
х
:
m
)
].
l)Страховые
договоры,
описанные
в
четвертой
и
в
пятой
строках,
предусматривают
пери
од
выплаты
премий,
который
короче,
чем
период,
в
котором
предусмотрены
выплаты
на
случай
смерти.
2)
Указанный
аннуитет
не
предусматривает
выплат
на
случай
смерти,
а
выплата
постоянных
премий
по
его
условиям
осуществляется
n
лет.
Другой,
возможно
более
реалистичный,
вид
анну
итета
с
постоянными
премиями,
отсроченными
на
n
лет,
описан
в
примере
6.6.2.

166
Гл.
6.
Нетто-премии
Формулу
(5.2.15)
можно
переписать
в
виде
(
1:-
)-1 _ 1 +
p(A
x
:
Тi1
)
ua
x
:Тi1
-
б'
откуда
следует,
что
2 - - 2
D[L] =
:А
х
:
т
-
(A
x
:
Тi1
)
•
у
(ба
х
:1ilР
Два
тождества,
(5.2.8)
и
(5.2.15),
можно
использовать
для
обнаружения
связи
между
непрерывно
выплачиваемыми
нетто-премиями.
Например,
исходя
из
(5.2.8),
имеем
- - 1
Р(
Ах)
=
::-
-
б
=
ах
Исходя
из
(5.2.15),
получаем
дa
x
:Тi1
+
A.
x
:
Тi1
=
1,
- - 1
P(A
x
:
1il
)
= -_- -
б
=
a
x
:i1I
- - 1
8 +
Р(А
х
)
=
::-,
ах
1 -
бах
БАх
ах
1 -
Ах'
- - 1
<5
+
P(A
x
:
Тi1
)
=
-_
-,
a
x
:Тi1
1 -
ба
х
:Тi1
БА
х
:
Тi1
a
x
:Тi1
1 -
A
x
:
Тi1
•
(6.2.9)
(6.2.10)
Словесная
интерпретация
дискретных
аналогов
формул
(6.2.9)
и
(6.2.10)
дается
в
примере
6.3.4.
Премии,
которые
обсуждались
нами
до
сих
пор,
были
нетто-премиями;
они
опре
делялись,
исходя
из
принципа
эквивалентности.
Перейдем
к
примеру,
в
котором
описываются
два
рассуждения,
при
которых
персентильные
премии
дают
неудовле
творительные
результаты.
Пример
6.2.3.
Вычислим
персентильиую
премию,
выбирая
25-ю
персентиль,
для
страхователя
возраста
55
лет и
для
следующих
страховых
планов:
(а)
смешанное
страхование
на
срок
20
лет,
(Ь)
страхование
на
случай
смерти
на
срок
20
лет,
(с)
страхование
на
случай
смерти
на
срок
10
лет.
Пусть
расчеты
производятся
в
непрерывной
модели,
интенсивность
начисления
процента
8
равна
0,06
и
данные
о
смертности
берутся
из
Иллюстративной
таблицы
смертности.
Решение.
(а)
Величина
потерь
для
смешанного
страхования
на
срок
20
лет
имеет
вид
L
=
{v
T
-
PaTI'
т
< 20,
20
--
V -
Ра2О1'
т
~
20.
Она
является
невозрастающей
функцией
от
Т.
Поэтому
те
значения
Т,
при
которых
потери
L
должны
быть
положительными
и
множество
которых
имеет
вероятность
0,25, -
это
значения,
которые
лежат
ниже
числа
~~25.
Поскольку
[55
= 86408,60
и
[70,617
= 64806,45
(что
получается
линейным
интерполированием),
Р(Т
<15,617) =
0,25.
Поэтому
персентильная
премия для
25-й
персентили
такова,
что
при
ней
потери
при
Т
=15,617
равны
нулю,
а
сама
она
равна
v
15
,617ja
15
,6171
=0,03865.

6.2.
Непрерывная
модель
167
(6.2.11)
(Ь)
Величина
потерь
для
страхования
на
случай
смерти
на
срок
20
лет
имеет
вид
L =
{vT_~
Ра:Т1'
т
< 20,
-
Pa2Ol,
т
~
20.
Это
по-прежнему
невозрастающая
функция
от
Т,
и
поскольку
Р(Т
<15,617)
=0,25,
величина
персентильной
премии для
25-й
персентили
снова
равняется
v
15
,617/a.
15
,6171 = 0,03865.
Конечно,
не
годится,
чтобы
одна
и
та
же
величина
пре
мии
соответствовала
двум
различным
страховым
планам,
особенно
если
учесть,
что
нетто-премия
для
лиц
рассматриваемого
возраста
по
договору
смешанного
страхо
вания
на
срок
20
лет
почти
в
два
раза
выше,
чем
по
договору
страхования
на
случай
смерти
на
срок
20
лет.
(с)
Величина
потерь
для
страхования
на
случай смерти
на
срок
10
лет
имеет
вид
L =
{v
T
_
-=
Рап,
т
< 10,
-
РаIOl'
т
~
10.
Если
назначается
нулевая
премия,
то
P(L
>
О)
=
Р(Т
<10),
и
эта
вероятность
равна
в
соответствии
с
Иллюстративной
таблицей
смертности
155 - 165 = 0,1281.
[55
Поэтому
нулевая
премия
является
наименьшей
неотрицательной
ежегодной
преми
ей,
такой,
что
вероятность
финансовых
потерь
страховщика
не
выше
0,25.
В
этом
случае
P(L>
О)
= 0,1281
и
Р
=
о
оказывается
персентильной
премией
для
25-й
персентили.
Нетто-премия
в
этом
случае
равна
70%
от
нетто-пр
ем
ии
для
договора
страхования
на
срок
20
лет.
~
В
качестве
вывода
из
рассмотренного
примера
заметим,
что
принцип
расчета
премий,
основанный
на
персентилях,
применительно
к
индивидуальному
страхова
нию
приводит
К
противоречивым
результатам.
В
дальнейшем
изложении
его
исполь
зование
будет
сведено
к
минимуму.
Для
бессрочного
страхования
на
случай
смерти,
согласно
определению,
содер
жащемуся
в
первой
строке
табл.
6.2.1,
т
--
L = v -
Рап,
Т
~
О.
Функцию
распределения
С.в.
L
можно
найти
следующим
образом:
FL(U)
=
P(L";
и)
=
Р
[v
T
-
Р
с
_/Т)
,,;
и]
=
Р
(v
T
~
бu
+
Р)
=
Р
[т
:>-
_! ln
(БU
+
Р)]
"
б+Р
:;--
б
б+Р
= 1 - F
T
(- ! ln
[дU
+
Р]
) -
Р
<
и
д
б+Р'
б
'
причем
функция
плотности
этой
случайной
величины
имеет
вид
(6.2.12)
168
Гл.
6.
Нетто-премии
Можно
считать,
что
эти
функции
распределения
индексированы
параметром
Р.
Используя
терминологию
теории
принятия
решений,
мы
можем
сказать,
что
опреде
ление
премии
Р
эквивалентно
выбору
распределения
с.в.
L,
задаваемого
формулой
(6.2.11),
который
будет
оптимальным
согласно
тому
принципу
расчета
премий,
ко
торым
руководствуется
лицо,
принимающее
решения.
Этот
принцип
отражает
пред
почтение
лица,
IIринимающего
решения.
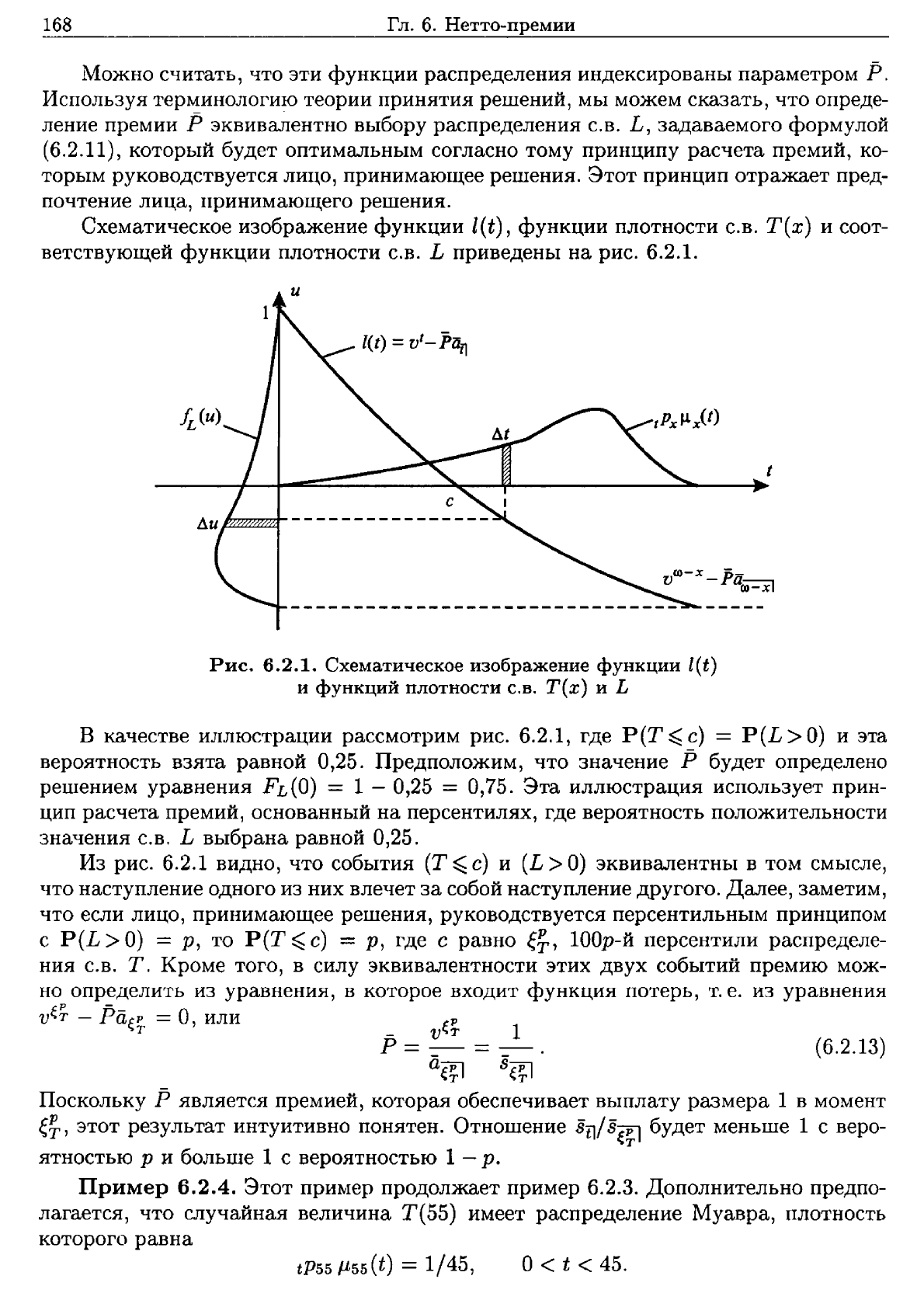
Схематическое
изображение
функции
l(t),
функции
плотности
С.в.
Т(х)
и
соот
ветствующей
функции
плотности
с.в.
L
приведены
на
рис.
6.2.1.
u
l(t) = v
t
-
Рап
t
Рис.
6.2.1.
Схематическое
изображение
функции
l(t)
и
функций
плотности
С.В.
Т(х)
и
L
(6.2.13)
-
V{~
1
Р
----
- -
а@
B~
Поскольку
Р
является
премией,
которая
обеспечивает
выплату
размера
1
в
момент
(~,
этот
результат
интуитивно
понятен.
Отношение
St1/S~
будет
меньше
1
с
веро-
ятностью
р
и
больше
1
с
вероятностью
1 -
р.
Пример
6.2.4.
Этот
пример
продолжает
пример
6.2.3.
Дополнительно
предпо
лагается,
что
случайная
величина
Т(55)
имеет
распределение
Муавра,
плотность
которого
равна
в
качестве
иллюстрации
рассмотрим
рис.
6.2.1,
где
Р(Т
~
с)
=
P(L
>
О)
и
эта
вероятность
взята
равной
0,25.
Предположим,
что
значение
Р
будет
определено
решением
уравнения
FL(O)
= 1 - 0,25 = 0,75.
Эта
иллюстрация
использует
прин
цип
расчета
премий,
основанный
на
персентилях,
где
вероятность
положительности
значения
С.в.
L
выбрана
равной
0,25.
Из
рис.
6.2.1
видно,
что
события
(Т
~
с)
и
(L
>
О)
эквивалентны
в
том
смысле,
что
наступление
одного
из
них
влечет
за
собой
наступление
другого.
Далее,
заметим,
что
если
лицо,
принимающее
решения,
руководствуется
персентильным
принципом
с
P(L
>
О)
=
р,
то
Р(Т
~
с)
=
р,
где
с
равно
~~,
100р-й
персентили
распределе
ния
С.в.
Т.
Кроме
того,
в
силу
эквивалентности
этих
двух
событий
премию
мож
но
определить
из
уравнения,
в
которое
входит
функция
потерь,
т.
е.
из
уравнения
еР
-
V'T
-
Pa~~
=
О,
или
tP55
Р55
(t) =
1/45,
О
< t < 45.

6.2.
Непрерывная
модель
169
Для
трех
рассматривавшихся
случайных
величин
потерь
выпишем
функции
распре
деления
с.в.
L
и
определим
значение
параметра
Р
как
наименьшее
неотрицательное
число,
такое,
что
P(L>
О)
~
0,25.
Решение.
(а)
Используя
формулу
(6.2.11)
и
учитывая,
что
функция
распреде
ления
имеет
скачок
в
точке
и
= v
20
-
Ра2О],
связанный
с
ограничением
на
L
при
Т
~
2О,
мы
приходим
К
следуюu~ему
семейству
функций
распределения,
индексиро
ванных
параметром
Р:
F
(и)
=
{~'
_1_ln[(0,06u
+
Р)/(0,06
+
Р)]
L + 0,06 45 '
1,
20
--
и
< v -
Ра2О1'
20
--
V -
Ра2О]
~
и
~
1,
1 <
и.
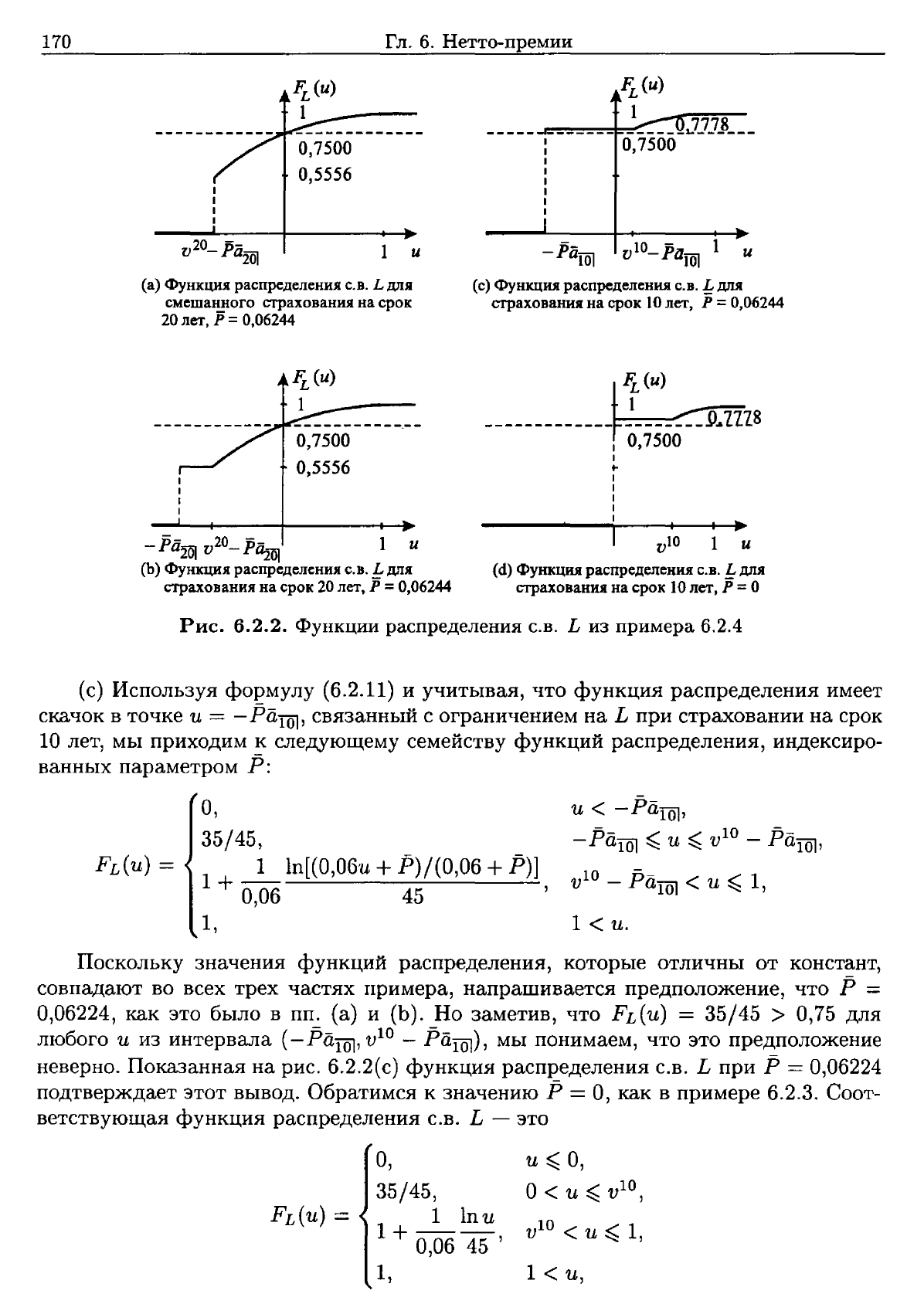
На
рис.
6.2.2(а)
изображена
функция
распределения,
которая
соответствует
сме
шанному
страхованию
на
срок
20
лет.
Этот
рисунок
позволяет
увидеть
графически
процесс
определения
премий
с
использованием
персентильного
принципа.
Мы
ищем
ту
функцию
распределения
из
семейства
распределений,
индексированного
пара
метром
Р,
которая
пересекает
вертикальную
ось
в
точке
0,75.
Аналитически
это
значит,
что
для
определения
премии
мы
решаем
относительно
Р
уравнение
или
1
1
ln[P/(0,06
+
Р)}
+ 0,06 45 = 0,75,
Т.е.
ln
(0,0:+
р).=
-0,675,
-
О
06е-
0
,675
р=-'---
1 -
е-
О
,675
откуда
1
--
= 0,06224.
811,251
В
свете
сказанного
по
поводу
соотношения
(6.2.11)
этот
результат
не
вызывает
удив
ления.
Если
в
качестве
распределения
С.в.
Т
выбирается
распределение
Муавра,
то
его
25-й
персентилью
будет
~~25
= 11,25.
Для
сравнения,
нетто-премия,
или
премия,
рассчитанная
по
принципу
эквива
лентности,
равна
в
этом
примере
-(А-
) _
J0
2
0(v
t
/45)
dt +(25/45) v
20
_
Р
55·20]
- 20 - 0,04456.
. J
o
v
t
(l - t/45)
dt
(Ь)
Используя
формулу
(6.2.11)
и
учитывая,
что
функция
распределения
имеет
скачок
в
точке
и
= -
Ра2О],
связанный
с
ограничением
на
переменную
потерь
при
страховании
на
случай
смерти
на
срок
20
лет,
мы
приходим
к
следующему
семейству
функций
распределения,
индексированных
параметром
Р:
О,
25/45,
1 1 ln[(0,06u +
]3)/(0,06
+
Р)]
+
006
45 '
,
1,
и
<
-Ра2О]
,
- - 20
--
-
Ра2О]
~
и
~
v -
Ра2Ol'
20
--
V -
Р
а
201
<
и
~
1,
1 <
и.
График
функции
распределения,
соответствующей
такому
страхованию
на
срок
20
лет,
показан
на
рис.
6.2.2(Ь).
Величина
премии
определяется
решением
уравнения
FL(O)
= 0,75
относительно
Р.
Пользуясь
п.
(а),
мы
снова
получаем
Р
= 0,06224.
170
0,7500
0,5556
Гл.
6.
Нетто-премии
~(и)
1 7778
-I_~_~_~_~_~_~_'="='_
~_.
---
-1..
_
0,7500
(а)
Функция
распределения
с.в.
L
для
смешанного
страхования
на
срок
20
лет,
Р
=0,06244
20
--
v
-Ра2Ol
1 u
--
10
- 1
-
PaIOl
v -
Pll
IOl
U
(с)
Функция
распределения
С.в.
L
для
страхования
на
срок
10
лет,
Р
= 0,06244
I •
0,7500
0,5556
-
Ра
20l
v
10
_
P~Ol
1 u
(Ь)
Функция
распределения
С.В.
L
для
страхования
на
сроlC
20
лет.
Р
=0,06244
_____________
~!t~U~-~9.1118
I 0,7500
I
..
I
I
I
I
I
v
10
1 u
(d)
Функция
распределения
с.в.
f
для
страхования
на
срок
10
лет,
Р
=
о
Рис.
6.2.2.
Функции
распределения
С.В.
L
из
примера
6.2.4
(с)
Используя
Фоемулу
(6.2.11)
и
учитывая,
что
функция
распределения
имеет
скачок
в
точке
U = -
РаIO],
связанный
с
ограничением
на
L
при
страховании
на
срок
10
лет,
мы
приходим
к
следующему
семейству
функций
распределения,
индексиро
ванных
параметром
Р:
О,
35/45,
1 1 ln[(0,06'u +
Р)/(0,06
+
Р)]
+
006
45 '
,
1,
u <
-РаIO]'
- -
10
--
-РаIQl
~
u
~
v - PaIQl,
10
--
V -
РаIO]
< U
~
1,
1 <
и.
Поскольку
значения
функций
распределения,
которые
отличны
от
констант,
совпадают
во
всех
трех
частях
примера,
напрашивается
предположение,
что
Р
=
0,06224,
как
это
было
в
пп.
(а)
и
(Ь).
Но
заметив,
что
FL(U)
=
35/45
> 0,75
для
любого
и
из
интервала
(-
PaIQl, v
10
-
Ращ),
мы
понимаем,
что
это
предположение
неверно.
Показанная
на
рис.
6.2.2(с)
функция
распределения
С.в.
L
при
Р
= 0,06224
подтверждает
этот
вывод.
Обратимся
к
значению
Р
=
О,
как
в
примере
6.2.3.
Соот
ветствующая
функция
распределения
С.в.
L -
это
О,
35/45,
1
lnu
1 +
006
45 '
,
1,
и
~
О,
О
<
и
~
v
10
-...;;:
,
v
10
<
и
~
1
-...;;:
,
1 <
и,
