Бауэрс Н., Гербер Х., Джанс Д., Несбитт С., Хикман Дж. Актуарная математика
Подождите немного. Документ загружается.


112
Гл.
4.
Страхование
жизни
предыдущем
разделе,
мы
употребляем
для
случайной
величины,
означающей
насто
ящую
стоимость
Zk+l,
символ
Z.
ДЛЯ
страхования
сроком
на
n
лет
при
выплате
размера
1
в
конце
года
смерти
{
1,
k = 0,1,
...
,n - 1,
b
k
+
1
=
О
в
противном
случае,
V
- V
k
+
1
k+l
- ,
Z =
{V
o
K
+
1
,
К
=
0,1,
...
,n - 1,
в
противном
случае.
Актуарная
настоящая
стоимость
для
такого
страхования
задается
формулой
n-l
А;:щ
=
E[Z]
=L v
k
+
1
kPx
Qx+k'
k=O
(4.3.2)
(4.3.3)
Заметим,
что
символ
для
актуарной
настоящей
стоимости
страховой
выплаты,
про
изводимой
в
конце
года
смерти,
принятый
в
Международной
системе
актуарных
обозначений,
совпадает
с
соответствующим
символом
для
случая
страховой
выпла
ты
в
момент
смерти
за
исключением
того,
что
убирается
черта
сверху.
Правило
моментов,
с
соответствующими
изменениями
в
обозначениях,
также
выполняется
для
страховых
выплат,
осуществляемых
в
конце
года
смерти.
Напри
мер,
для
страхового
договора
на
срок
n
лет,
рассматривавшегося
выше,
n-l
D[Z]
2Аl
(А
1
)2
2А
1
_
"'"
-2б(k+l)
=
х:щ
-
х:т,
где
х:щ
-
~
е
kPx
qx+k·
k=O
В
разд.
3.5
выводятся
рекуррентные
соотношения
для
ожидаемых
продолжительно
стей
жизни,
которые
далее
используются
для
вычисления
их
значений.
Рекуррент
ные
соотношения
для актуарных настоящих
стоимостей
страхования
на
фиксиро
ванный
срок
можно
вывести
алгебраически
из
соотношения
(4.3.2):
n-1
n-l
n-l
А;;щ
= L v
k
+
1
kPx
Qx+k
=
vqx
+L V
k
+
1
kPx
qx+k
=
vqx
+
Vpx
L v
k
k-lРх+l
Qx+k
k=O
k=l
k~l
n-2
"'"
'+1
1
=
vqx
+
Vpx
~
V
J
jPx+l
Qx+l+j
=
vQx
+
Vpx
А
х
+
1
:
n
-
1I
·
j=O
Чтобы
равенства
(4.3.3)
выполнялись
при
n = 1,
мы
положим
А;:Ol
=
О
для
всех
х.
Замечание.
Если
проводилась
селекция,
то
в
формуле
(4.3.3)
все
х
в
индексах
должны
быть
заключены
в
квадратные
скобки.
Пример
4.3.1.
На
основе
Иллюстративной
таблицы
смертности
при
i = 0,04
определим
математическое
ожидание
и
дисперсию
случайной
величины,
равной
на
стоящей
стоимости
страхования
на
срок
1
О
лет
с
выплатой
размера
1,
производимой
В
конце
года
смерти
страхователя,
который
заключил
договор
страхования
в
возра
сте
30
лет.

4.3.
Страховые
выплаты,
производимые
в
конце
года
смерти
113
Решение.
Отправляясь
от
начального
значения
A
4
1
0
:
01
=
О
И
используя
формулу
(4.3.3),
принимающую
для
нашего
случая
вид
АЗО~k:l0-kl
=
vqЗО+k
+
VРЗО+k
АЗО+~+1:10-(k+l)1'
k =
0,1,
...
,8,9,
мы
получаем,
двигаясь
от
возраста
40
к
возрасту
30
лет,
Аз~:IOl
= 0,01577285
и
D[Z] = 0,01271978 - (0,01577285)2 = 0,1247099.
Эти
значения
были
получены
с
использованием
таблицы,
построенной
в
разделе
«Упражнения
с
использованием
компьютера~
гл.
3.
~
Модель
для
договора
бессрочного
страхования,
заключенного
с
лицом
(х),
мож
НО
построить,
устремив
n
к
бесконечности
в
модели
страхования
на
срок
n
лет.
Для
актуарной
настоящей
стоимости
мы
получим
формулу
00
Ах
= L V
k
+
1
kPx
Qx+k·
k=O
Умножая
обе
части
формулы
(4.3.4)
на
lx,
получим
(4.3.4)
(4.3.5)
(4.3.6)
00
lxAz
= L V
k
+
1
dx+k.
k=O
Формула
(4.3.5)
отражает
равенство
в
момент
заключения
договора
страхования
выражений
для
суммы
этих
актуарных
настоящих
стоимостей
для
lz
лиц,
застрахо
ванных
в
возрасте
х,
и
для
величины,
на
которую
уменьшается
фонд
в
результате
ожидаемых
смертей
lx
лиц.
Выражение
00
L
Vk+1dx+k
k=r
соответствует
той
части
фонда
в
момент
заключения
договора
страхования,
которая
вместе
с
процентами,
полученными
при
предполагаемой
процентной
ставке,
обеспе
чит
страховые
выплаты
в
связи
с
ожидаемыми
смертями
после
т-го
страхового
года.
Величина
(4.3.6)
при
предполагаемой
процентной
ставке
в
течение
т
лет
дает
00
"'"
v
k
-
r
+
1
d
L.J
x+k,
k=r
(4.3.7)
ожидаемую
величину
средств
по
истечении
т
страховых
лет.
Сравнение
выраже
ний
(4.3.7)
и
(4.3.5)
показывает,
что
эта
величина
равна
lх+rАж+r.
Разница
между
этой
величиной
и
фактическим
размером
фонда
объясняется
отклонениями
числа
произошедших
смертей
от
числа
ожидаемых
смертей
(в
соответствии
с
принятой
та
блицей
смертности)
и
отклонениями
реального
процентного
дохода
от
процентного
дохода
при
предполагаемой
процентной
ставке.
Пример
4.3.2.
Группа
из
100
лиц
в
возрасте
30
лет
учреждает
фонд
для
выпла
ты
в
конце
года
смерти
любого
из
участников
суммы
1000
выбранному
участнику
из
числа
оставшихся
в
живых.
Они
приходят
к
взаимному
соглашению
внести
в
фонд
сумму,
равную
актуарной
настоящей
стоимости
бессрочного
страхования,
вычис
ленную
на
основе
Иллюстративной
таблицы
смертности
с
процентной
ставкой
6%.

114
Гл.
4.
Страхование
жизни
Участники,
для
которых
никакая
страховая
компания
не
проводила
селекцию,
ре
шают
использовать
эту
таблицу
в
качестве
основы
своего
плана.
Фактический
опыт
этого
фонда
показывает,
что
происходит
одна
смерть
в
каждый
второй
и
каждый
пятый
годы.
Процентный
доход
составляет
в
первый
год
6%,
во
второй
и
в
третий
годы
6,5
%,
в
четвертый
и
в
пятый
годы
7%.
Какова
разница
между
ожидаемым
раз
мером
фонда,
определяемым
в
начале
его
деятельности,
и
его
реальным
значением
к
концу
первых
5
лет?
Решение.
Согласно
договоренности,
1000А
зо
= 102,4835,
так
что
при
100
участ
никах
фонд
имеет
в
начале
своей
деятельности
сумму
10248,35.
Далее,
А
З5
=
0,1287194
и
lЗ5/lзо
= 0,9915040.
Для
100
лиц
возраста
30
ожидаемая
величина
фонда
по
протествии
5
лет
со
ставит
(1000) (100)
llЗ5
= 12762,58.
зо
Обозначим
через
F
k
величину
фонда
к
концу
страхового года
с
номером
k.
Дина-
мика
реального
фонда
будет
следующей:
Р
О
= 10248,35,
Р
1
= (10248,35)(1,06) = 10863,25,
F
2
= (10863,25)(1,065) - 1000 = 10569,36,
F
з
= (10569,36)(1,065) = 11256,37,
F
4
=(11256,37)(1,07) =12044,32,
Р
5
= (12044,32)(1,07) - 1000 = 11887,42.
Таким
образом,
искомая
разница
составит
12762,58 - 11887,42 = 875,16.
Этот
ре
зультат
объединяет
опыт
инвестирования
и
смертности
за
5-летний
период.
При
инвестировании
доходы
превысили
запланированные
на
уровне
6%.
С
другой
сторо
ны,
потери
за счет
смертности
оказались
больше:
две
смерти
по
сравнению
с
числом
0,8496.
Интерпретация
этих
результатов
в
терминах
взаимного
влияния
различных
факторов,
таких,
как
инвестиционный
доход
и
уровень
смертности,
является
про
фессиональной
обязанностью
актуария.
~
Мы
вывели
рекуррентные
соотношения
(4.3.3)
для
актуарной
настоящей
стоимо
сти
страхования
на
случай
смерти
сроком
на
n
лет
алгебраическими
методами.
Хотя
эти
соотношения
будут
справедливы
для
актуарной
настоящей
стоимости
бессроч
ного
страхования
на
случай
смерти,
поскольку
это
предельный
случай
страхования
на
n
лет
при
n --t
00,
мы
установим
их
независимым
образом,
чтобы
проиллюстри
ровать
вероятностные
методы
доказательства.
Рассмотрим
выражение
Ах,
обращаясь
к
его
определению
E[Z] = E[v
K
(x)+l].
Для
удобства читателя
перепишем
его
в
виде
Ах
=E[Z] =E[v
K
(x)+ll
К(х)
~
О],
хотя
эта
запись
избыточна,
поскольку
вся
вероятностная
масса
распределения
С.в.
К(х)
сосредоточена
на
множестве
неотрицательных
целых
чисел.
Величину
E[Z]
можно
вычислить,
рассматривая
событие,
что
лицо
(х)
умрет
в
первый
год,
т.
е.
К(х)
=
О,
и
его
дополнение,
событие,
что
лицо
(х)
переживет
первый
год,
т. е.
К(х)
~
1.
Мы
можем
записать
E[Z] =E[v
K
(x)+ll
К(х)
=
О]
Р[К(х)
=
О]
+E[v
K
(x)+lj
К(х)
~
1]
Р[К(х)
~
1].
(4.3.8)

4.3.
Страховые
выплаты,
производимые
в
конце
года
смерти
в
этом
выражении
мы
можем
сделать
следующие
очевидные
замены:
E[v
K
(X)+l!
К(х)
=
О]
= v,
Р[К(х)
=
О]
=
qx
И
Р[К(х)
~
1]
=
РХ.
115
Для
того
чтобы
найти
выражение
для
оставшегося
сомножителя,
перепишем
его
в
виде
E[v
K
(X)+ll
К(х)
~
1]
=
vE[v(K(x)+l)+ll
К(х)
- 1
~
О].
Так
как
С.в.
К(х)
является
пошаговой
продолжительностью
предстоящей
жизни
лица
(х)
при
условии
К(х)
~
1,
то
С.в.
К(х)
- 1
должна
быть
пошаговой
продол
жительностью
предстоящей
жизни
лица
(х
+ 1).
Если
мы
хотим
использовать
те
же
вероятности
для
условного
распределения
С.В.
К(х)
- 1
при
условии
К(х)
~
1,
как
если
бы
с
самого
начала
рассматривалось
лицо
возраста
х
+ 1,
мы
можем
написать
E[V(K(x)+l)+l
I
К(х)
- 1
~
О]
=
А
х
+
1
и,
подставив
эту
величину
в
(4.3.8),
получить
Ах
=
vqx
+
vA
x
+
1
px.
(4.3.9)
(4.3.10)
Предложение
(распределение
продолжительности
предстоящей
жизни
лица
возраста
х
+ 1,
с
которым
заключен
договор
страхования
в
настоящий
момент)
=
(распределение
продолжительности
предстоящей
жизни
лица
возраста
х
+1
в
настоящий
момент,
с
которым
заключен
договор
страхования
1
год
тому
назад)
обсуждалось
в
разд.
3.8.
В
терминах
селекционных
таблиц
правая
часть
равенства
(4.3.9)
будет
иметь
вид
А[Х]+l'
В
соотношении
(4.3.10)
каждый
символ
х
должен
быть
заменен
на
[х].
Заметим,
что
(4.3.10)
является
такой
же
обратной
рекуррентной
формулой,
что
и
(4.3.3),"а
именно
формулой
вида
u(х)
=
vqx
+vpx
u(х
+ 1).
Именно
начальное
значение
определяет,
будет
ли
ее
решение
актуарной
настоящей
стоимостью
бессрочного
страхования
на
случай
смерти
или
актуарной настоящей
стоимостью
страхования
на
срок
n
лет.
Та
же
рекуррентная
формула
получается
и
для актуарных
настоящих
стоимостей
смешанного
страхования
сроком
на
n
лет,
где
начальными
значениями
является
стоимость
в
момент
n.
Анализ
соотношения
(4.3.10)
способствует
пониманию
природы
величины
Ах.
После
замены
Рх
на
1 -
qx
и
умножения
обеих
частей
на
(1
+ i)lx
соотношение
(4.3.10)
можно
переписать
в
виде
(4.3.11)
Для
совокупности
случайного
дожития
это
соотношение
имеет
следующую
интер
претацию.
Вместе
с
процентами
за
первый
год
величина
Ах,
умноженная
на
lx,
среднее
число
лиц,
доживших
до
возраста
х,
дает
величину
А
х
+
1
,
умноженную
на
lx
и,
кроме
того,
величину
1 -
А
х
+
1
,
умноженную
на
число
d
x
лиц,
смерть
которых
ожидается
В
течение
этого
года.
Такая
величина
для
каждой
ожидаемой
смерти,

116
Гл.
4.
Страхование
жизни
qж(l
-
А
ж
+
1
),
называется
годовой
стоимостью
страхова'Н,ия.
Величина
А
ж
+
1
ка
сается
доживших
и
умерших,
в
то
время
как
величина
1 -
А
х
+
1
касается
только
умерших.
Деля
на
lж
и
затем
вычитая
Аж
+qх(1-А
ж
+
1
)
из
обеих
частей
формулы
(4.3.11),
мы
получаем
(4.3.12)
Иначе
говоря,
разница
между
актуарными настоящими
стоимостями
для
лиц
воз
раста
х
лет
и
возраста
х
+1
лет
равна
процентам
,
начисленным
на
актуарную
на
стояшую
стоимость
в
возрасте
х
минус
годичная
стоимость
страхования
в
этот
год.
Другое
выражение
для
Ах
можно
получить
из
формулы
(4.3.10),
заменив
Рх
на
1 -
qж,
умножив
обе
части
на
V
x
и
перегруппировав
ее
члены.
В
результате
мы
получаем
х+1А
ХА
-
х+1
(1
А
)
v
х+1
- V
ж
-
-v
qx -
х+1,
или
~vx
Ах
=
-v
x
+
1
qx(1 -
А
х
+
1
).
Суммируя
ОТ
х
=
у
до
00
(см.
приложение
5),
мы
получим
00
-vУА
у
=-
Lv
Х
+
1
qж(1-
А
х
+
1
)
ж=у
и,
таким
образом,
00
Ау
=
Lv
х
+
1
-
У
qж(1-
А
ж
+
1
).
ж=у
Это
выражение
показывает,
что
актуарная
настоящая
стоимость
для
возраста
у
равна
сумме
настоящих
стоимостей
в
момент
у
годовых
стоимостей
страхования
по
всему
времени
предстоящей
жизни
страхователя.
Смешанное
страхование
на
срок
n
лет
с
выплатой
размера
единица
в
конце
года
смерти
является
комбинацией
рассмотренного
в
этом
разделе
страхования
на
срок
n
лет и
страхования
на
дожитие
на
срок
n
лет
с
выплатой
размера
единица,
которое
обсуждалось
в
предыдущем
разделе.
Такому
договору
соответствуют
функции
k = 0,1,
...
,
k =
О,1,
...
,n
-
1,
k =n, n + 1,
...
,
J(
=
0,1,
.
..
,n
-
1,
К
=
n,n
+
1,
....
Актуарная
настоящая
стоимость
равна
(4.3.13)
n-1
А
-"
k+1
+ n
х:щ
- L..i v
kPx
Qx+k v
nРх'
k=O
Бессрочное
страхование
на
случай
смерти
с
ежегодно
увеличивающейся
выпла
той,
когда
выплачивается
k + 1
единиц
в
конце
k +
1-го
года
действия
договора,
4.3.
Страховые
выплаты,
производимые
в
конце
года
смерти
117
если
страхователь
умрет
в
этом
страховом
году,
имеет
следующие
функции
выплат
и
дисконтирования
и
случайную
величину
настоящей
стоимости:
b
k
+
1
= k +1,
k+l
Vk+l
= V ,
Z =
(К
+1)v
K
+
1
,
k =
0,1,2,
,
k =
0,1,2,
,
К
=
0'1'2'
.
k =
0,1,
...
,
k =
О,1,
...
,n-
1,
k =
n,n
+
1,
...
,
Его
актуарная
настоящая
стоимость
обозначается
через
(1
А)х.
Страхование
на
срок
n
лет
с
ежегодно
уменьшающейся
выплатой
в
течение
n-летнего
периода
предусматривает
выплату
в
конце
года
смерти,
равную
n -
k,
где
k -
число
полных
лет,
прожитых
страхователем
с
момента
заключения
договора.
Соответствующие
функции
имеют
вид
{
n-
k
b
k
+1 = '
О,
V
-vk+l
k+l
- ,
К
=
0,1,
.
..
,n
-
1,
К
=
n,n
+ 1,
....
Актуарная
настоящая
стоимость
для
этого
страхования
обозначается
символом
(пA)~:т'
8 ......
---.
Страхование
на
срок
1
год,
отсроченное
на
1
год;
с
ВЫIVIатой
7
единиц
7
6
5
4
3
2
I
Страхование
на
срок
1
год,
отс
оченное
на
2
года,
с
выплатой
1
единицы
Страхование
на
срок
6
лет
с
выплатой
1
единицы
о
1
2 3 4 5
6 7
8
k
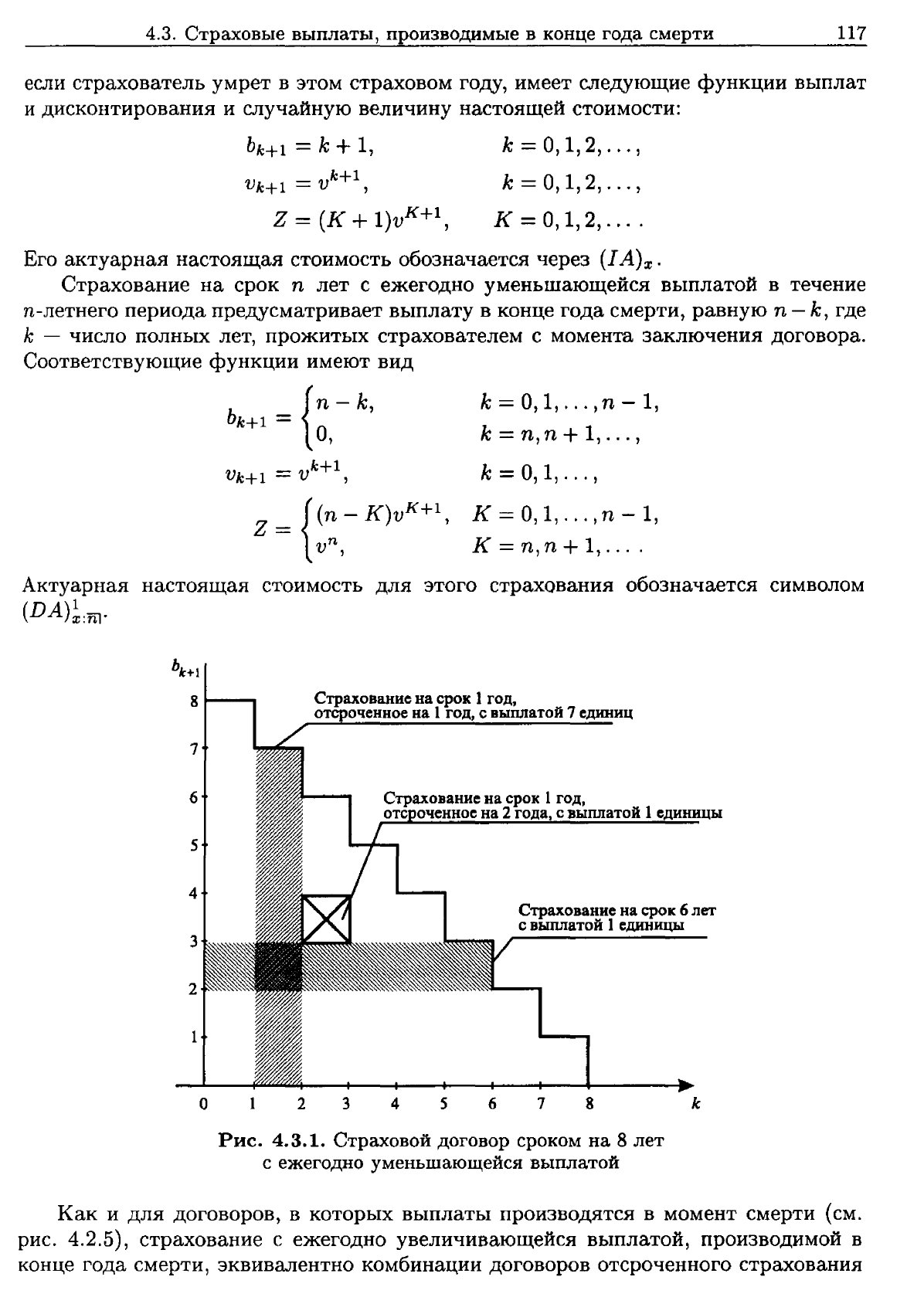
Рис.
4.3.1.
Страховой
договор
сроком на
8
лет
с
ежегодно
уменьшающейся
выплатой
Как
и
для
договоров,
в
которых
выплаты
производятся
в
момент
смерти
(см.
рис.
4.2.5),
страхование
с
ежегодно
увеличивающейся
выплатой,
производимой
в
конце
года
смерти,
эквивалентно
комбинации
договоров
отсроченного
страхования

118
Гл.
4.
Страхование
жизни
на случай
смерти
с
постоянными
выплатами
размера
единица.
Аналогично,
срочное
страхование
с
ежегодно
уменьшающейся
выплатой
эквивалентно
комбинации
стра
ховых
договоров
с
постоянными
выплатами
и
разными
сроками
действия.
Ри(!унок
4.3.1
иллюстрирует
сказанное
для
страхования
на
8
лет
с
ежегодно
уменьшающейся
выплатой.
На
рис.
4.3.1
изображен
график
функции
выплат
bk+l'
Каждый
единичный
квадрат
представляет
договор
отсроченного
страхования
сроком
на
1
год.
Когда
они
объединяются
по
вертикали,
получаются
договоры
отсроченного страхования
сроком
на
1
год
и
с
уменьшающимися
выплатами.
Когда
квадраты
объединяются
по
горизонтали,
получаются
срочные
договоры
страхования
с
постоянными
выплатами
разной
длительности.
Такие
вертикальные
и
горизонтальные
способы
объединения
также
показаны
на
рис.
4.3.1.
Тот
факт,
что
актуарные
настоящие
стоимости
комбинации
договоров
срочного
страхования
с
постоянными
выплатами
и
актуарные
настоящие
стоимости
комби
нации
договоров
срочного
отсроченного
страхования
равны,
можно
выразить
ана
литически.
Так,
согласно
определению,
n-l
n-l
n-l
(DA)~:nJ
=
L(n
-
k)v
k
+
1
kPx
Qx+k
=
L(n
-
k)(vkkPx)(vQx+k)
=
L(n
-
k)
kll
A
x,
k=O
k=O
k=O
(4.3.14)
что
соответствует
суммированию
по
вертикали.
Произведя
подстановку
n - k =l:;==-ok-l(l)
в
формулу
(4.3.14),
мы
получим
n-ln-k-l
(DA);:nJ = L L (1) V
k
+
1
kPx
Qx+k
.
k=O
j=o
Меняя
порядок
суммирования,
мы
получим
n-l
n-j-l
L L (1) v
k
+
1
kPx
Qx+k
з=О
k=O
и,
сравнивая
сумму
по
k
с
(4.3.2),
можем
записать
n-l
(DA);:m = L A;:n_j!'
j=O
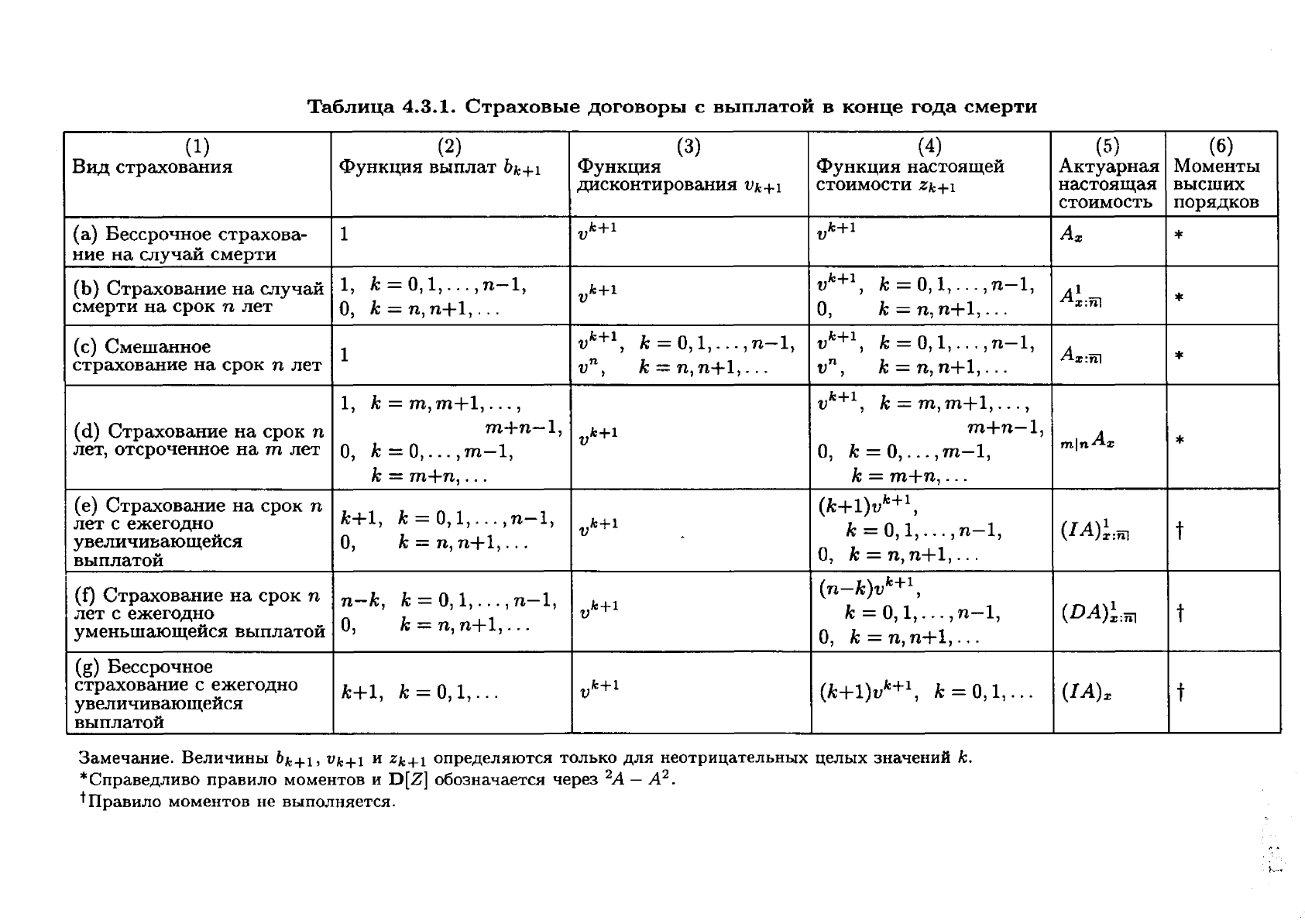
В
табл.
4.3.1
приведена
сводка
функций
и
обозначений
для
элементарных
дого
воров
страхования,
в
которых
выплаты
производятся
в
конце
года
смерти.
Мы
завершаем
этот
раздел
сводкой
рекуррентных
соотношений
для
актуарных
настоящих
стоимостей
страхования
для
случая,
когда
выплаты
производятся
в
кон
це
года
смерти.
Рассмотрим
приведенные
ниже
соотношения
(a)-(g),
расположенные
в
том
порядке,
в
каком
соответствующие
виды
страхования
входят
в
табл.
4.3.1.
Для
каждого
из
перечисленных
в
таблице
видов
страхования
приводится
рекуррентное
соотношение,
область
изменения
переменной
и
начальное
условие.
Значения
акту
арных
настоящих
стоимостей
следует
вычислять,
начиная
с
наименьшего
возраста,
приведенного
в
таблице
смертности,
и
до
возраста
у
или
W.
Таблица
4.3.1.
Страховые
договоры
с
выплатой
в
конце
года
смерти
(1)
(2)
(3)
(4)
(5)
(6)
Вид
страхования
Функция
выплат
bk+l
Функция
Функция
настоящей
Актуарная
Моменты
дисконтирования
Vk+l
стоимости
Zk+l
настоящая
высших
стоимость
порядков
(а)
Бессрочное
страхова-
1
V
k
+
1
v
k
+
1
Ах
*
ние
на
случай
смерти
(Ь)
Страхование
на
случай
1,
k =
0,1",
.
,п-1,
V
k
+
1
V
k
+
1
k=0,1,
...
,n-1,
А~;щ
,
*
смерти
на
срок
n
лет
О,
k =
п,п+1,
...
О,
k =
п,п+1,
...
(с)
Смешанное
V
k
+
1
k =0,1,
...
,
п-1,
V
k
+
1
k =
0,1",
. ,
п-1,
А
х
:
щ
1
,
,
*
страхование
на
срок
n
лет
v
n
k =
п,п+1,
...
v
n
k =
п,п+1,
...
,
,
1,
k=т,т+1",.,
V
k
+
1
k=т,т+1,
..
"
,
(d)
Страхование
на
срок
n
т+п-1,
v
k
+
1
т+п-1,
mln
Ax
*
лет,
отсроченное
на
т
лет
О,
k =
О,
..
,
,т-1,
О,
k=0"
..
,т-1,
k =
т+п,
...
k
=т+п,
...
(
е)
Страхование
на
срок
n
k+1,
k =0,1,
...
,п-1,
(k+1)v
k
+
1
,
лет
с
ежегодно
vk+l
k
=
О,
1,
...
,
п-1,
(1
А);:щ
t
увеличивающейся
О,
k =
п,п+1,
...
.
выплатой
О,
k =
п,п+1,
...
I
(n-k)v
k
+
1
,
(1)
Страхование
на
срок
n
n-k
k =
0,1,
...
,
n-l,
лет
с
ежегодно
,
V
k
+
1
k =
О,
1,
...
,
n-l,
(пА);;щ
t
уменьшающейся
выплатой
О,
k =
п,п+1,
...
О,
k =
п,п+l,
...
(g)
Бессрочное
страхование
с
ежегодно
k+l,
k =
0,1,
...
V
k
+
1
(k+1)v
k
+
1
,
k =0,1,
...
(1А)х
t
увеличивающейся
выплатой
Замечание.
Величины
b
k
+
1
,
Vk+l
и
Zk+l
определяются
только
для
неотрицательных
целых
значений
k.
*Справедливо
правило
моментов
и
D[Z]
обозначается
через
2А
-
А2.
t
Правило
моментов
не
выполняется.
k·.

120
Гл.
4.
Страхование
жизни
(а)
Аж
=vqx +
VРж
А
ж
+
1
,
х
=
0,1,
...
,и.;
- 1,
и
А""
=
о.
(Ь)
А
1
~
=
vqж
+
Vpx
А
1
()
l'
х
=
О,
1,
...
,
у
- 1,
и
А
1.(51
=
О.
Х:У-ЖI
х+l:у-
ж+l
y.ul
(с)
А
ж
:
у
-
жl
= vqx +
Vpx
A
x
+
1
:
y
-(X+l)l'
Х
= 0,1, ,
у
- 1,
и
А
у
:
О1
=
о.
(d)
Y-хlnАж
=
0+
vpx
y-(х+l)lnАх+l,
х
=
0,1,
,у
- 1,
и
OlnAy
= At:rn'
(е)
(1
A)~:y_xl
=
[vqx
+vpx
АХ~I:У_(Ж+l)IJ
+vpx
(IА)Ж~I:У_(:Z;+I)1'
Х
=0,1,
...
,
у
- 1,
и
(1
A)~:Ol
=
о.
(f)
(DA)~:y_xl
= (y-x)vq:z;+vpx
(DA)x~l:y_(:Z;+I)I'
Х
= 0,1,
...
,у-1,
и
(пA)~:Ol
=
о.
(g)
(1
А)х
=
[vqж
+VPxAx+l) + vpx
(1
А)х+l,
х
=
0,1,
...
,w - 1,
и
(1
А)""
=
О.
Замечания.
1.
В
этом
разделе
обоснованы
только
соотношения
(а)
и
(Ь).
Соот
ношения
пп.
от
(с)
до
(g)
обосновываются
аналогичным
образом.
2.
Все
семь
соотношений
имеют
вид
u(х)
=
с(х)
+
vp:z;
u(х
+ 1),
где
с(х)
-
заданная
функция,
определенная
в
области
определения
соответствую
щего
соотношения.
На
языке
дифференциальных
уравнений
всем
семи
формулам
соответствует
одно
и то
же
однородное
уравнение
u(х)
= vpx
u(х
+1).
Оно
является
линейным,
но
его
коэффициенты
непостоянны.
3.
Поскольку
с(х)
=
vqж
для
(а),
(Ь)
и
(с),
соответствующие
актуарные
насто
ящие
стоимости
получаются
из
одних
и
тех
же
рекуррентных
формул,
различаю
щихся
только
начальными
значениями.
4.4.
Соотношения
между
страховыми
договорами
с
выплатами
в
момент
смерти
и
в
конце
года
смерти
Мы
начнем
изучение
этих
соотношений
с
анализа
актуарной
настоящей
стоимо
сти
для
договора
бессрочного
страхования
на
случай
смерти,
по
которому
произво
дится
выплата
размера
единица
в
момент
смерти.
В
силу
формулы
(4.2.6)
-
[00
t
[1
t
/,00
t
Аж
=
10
v
tPx
ILx(t)
dt
=
10
v
tPx
ILx(t) dt + 1 v
tPx
ILx(t) dt.
Замена
переменных
s = t - 1
ВО
втором
интеграле
дает
Ах
=
11
v
t
tPx I-'x(t)
dt
+v
100
v'
в+IРх
I-'x(8
+1) d8. (4.4.1)
На
основе
данных
агрегативной
таблицы
смертности
в+IРх
ILx(S
+
1)
=
Рх
ВРХ+l
J.L(x
+S +1),
и
второе
слагаемое
в
формуле
(4.4.1)
есть
vpx
А
х
+
1
•
На
основе
данных
селекцион
ной
таблицы
смертности
второе
слагаемое
в
формуле
(4.4.1)
есть
VP[x]
A[xJ+l'
Воз
вращаясь
к
(4.4.1)
и
пользуясь
обозначениями
из
агрегативных
таблиц
смертности,
получаем
[1
Ах
=
Jo
vttPxlLx(t)dt
+
VPx
A
x+l
=A~:Il+vPxAx+l'
(4.4.2)
Принимая
одно
из
соглашений
о
форме
функции
смертности
в
промежутках
между
целыми
точками,
которые
обсуждались
в
разд.
3.6,
интеграл
в
(4.4.2)
можно
выра
зить
через
значения
функций
из
дискретной
таблицы
смертности.

4.4.
Страхование
с
выплатами
в
момент
смерти
и
в
конце
года
смерти
121
в
предположении
равномерности
распределения
моментов
смерти
внутри
каж
дого
годичного
возрастного
интервала
имеем
tPy
f.ty(t) = qy,
о
~
t
~
1
и
у
= 0,1,
...
,
что
можно
подставить
в
формулу
(4.4.2),
получив
А.
=q.
101
v'
dt +
vp.
А,
н
=
~
vq. +
vp.
А.
н
.
(4.4.3)
Величина
х
в
этом
соотношении
принимает
значения
О,
1,
...
,(;J
- 1,
а
начальное
значение
A
w
равно
О.
Если
мы
умножим
обе
части
рекуррентной
формулы
(а)
на
i/б,
то
получим
~A.
=
~vq.
+VP.(~A.H).
Поскольку
формулы
(а)
и
(4.4.3)
выражают
одну
и
ту
же
рекуррентную
формулу,
имеют
одинаковую
область
изменения
х
и
одинаковые
начальные
значения
О
в
точке
w,
величина
(i/w)A
x
является
решением
для
(4.4.3)
и
-
~
Ах
=
б
Ах·
(4.4.4)
В
предположении
равномерности
распределения
моментов
смерти
внутри
годичных
возрастных
интервалов
формулу
(4.4.4)
можно
было
бы
угадать.
Воздействие
пред
положения
о
равномерности
состоит
в
том,
что
выплаты
размера
1,
производимые
в
момент
смерти,
эквивалентны
выплатам
размера
1
в
год,
производимым
непрерыв
но
в
течение
всего
года,
в
котором
произошла
смерть.
Если
учитывать
проценты,
то
выплаты
размера
1
в
год,
производимые
непрерывно
в
течение
всего
года,
в
котором
произошла
смерть,
эквивалентны
выплате
суммы
i/
б
в
конце
этого
года.
Тождество
(4.4.4)
можно
получить,
используя
свойства
случайной
величины
«продолжительность
предстоящей
жизни»
в
предположении
равномерности
распре
деления
смертей
в
годичных
возрастных
интервалах,
как
это
делалось
в
разд.
3.6.
Воспользовавшись
формулой
(3.6.1),
мы
запишем
Т
=
К
+
В.
Мы
отмечали,
что
в
предположении
равномерности
распределения
смертей
в
годичных
возрастных
интервалах
с.в.
К
и
S
независимы
и
С.в.
S
имеет
равномерное
распределение
на
единичном
интервале.
В
качестве
следствий
из
этих
наблюдений
получаем, что
С.в.
К
+ 1
и
1 - S
также
независимы
и
С.в.
1 - S
имеет
равномерное
распределение
на
единичном
интервале.
В
тождестве
Ах
=E[v
T
]
=E[v
K
+1
(1
+
i)l-S]
мы
можем
воспользоваться
независимостью
С.в.
К
+1
и
1- S
для
вычисления
мате
матического
ожидания
произведения
как
произведения
математических
ожиданий,
E[v
K
+
1
(1
+
i)I-S]
= E(vK+l]
Е[(l
+
i)I-S].
(4.4.5)
Первый
сомножитель
в
правой
части
равен
Ах.
Поскольку
с.в.
1-
S
имеет
равномер
ное
распределение
на
единичном
интервале,
для
второго
сомножителя
справедливо
равенство
1
1 .
Е[(l
+
i)l-S]
=
(1
+i)t1 dt =
.!..
о
б
Таким
образом,
в
предположении
равномерности
распределения
смертей
в
годичных
интервалах
мы
снова
имеем
Ах
= (i/
б)А
х
.
