Бауэрс Н., Гербер Х., Джанс Д., Несбитт С., Хикман Дж. Актуарная математика
Подождите немного. Документ загружается.


102
Гл.
4.
Страхование
жизни
Теперь
мы
обращаем
внимание
на
одно
стандартное
приложение,
касающееся
портфеля
рисков:
определение
величины
начального
инвестиционного
фонда
для
портфеля
страховых
договоров.
Мы
будем
использовать
модель
индивидуальных
рисков
и
нормальную
аппроксимацию
(см.
обсуждение
в
разд.
2.4).
Пример
4.2.3.
Предположим,
что
каждое
из
100
независимых
лиц
•
имеет
возраст
х,
•
подвержено
постоянной
интенсивности
смертности,
р..
=0,04,
•
заключило
договор
страхования
с
выплатой
10
единиц
в
момент
смерти.
Страховые
выплаты
производятся
из
средств
инвестиционного
фонда,
причем
д
= 0,06.
Рассчитаем
минимальную
величину
фонда
h
в
момент
t =
О,
чтобы
средств
для
страховых
выплат
на
случай
смерти
каждого
из
страхователей
оказалось
доста
точно
с
вероятностью
приблизительно
0,95.
Решение.
Для
каждого
лица
b
t
= 10, t
~
О,
V
-
v
t
t - ,
t
~
О,
Z = 10v
T
,
Т
~
О.
E[z2] =
10
22
А
= 100 0,04 = 25
х
0,04 + 2(0,06)
Будем
считать,
что
страхователи
каким-либо
образом
перенумерованы,
например,
номерами
заключенных
с
ними
договоров.
Тогда
в
момент
t =
О
настоящая
стои
мость
всех
предстоящих
выплат
равна
100
S=LZj,
1
где
Zj
является
настоящей
стоимостью
в
момент
времени
t =
О
той
выплаты,
кото
рую
придется
произвести
в
момент
смерти
лица
с
номером
j.
Для
того
чтобы
подсчитать
среднее
и
дисперсию,
заметим,
что
С.в.
Z
равна
слу
чайной
величине,
являющейся
умноженной
на
10
настоящей
стоимостью
бессроч
ного
страхования
на случай
смерти
с
выплатой
размера
единица.
Для
постоянной
интенсивности
начисления
процента
б
и
постоянной
интенсивности
смертности
jJ
ак
туарная
настоящая
стоимость
бессрочного
страхования
жизни
с
выплатой
величины
единица
равна
Ах
=
[00
e-
6t
е-J.Ltр..dt
=
р..
.
Jo
р..
+
б
Таким
образом,
для
нашего
примера
[
- 0,04
Е
Z]
=
10А
х
= 10 - =
4,
0,1
и
D[Z] = 9.
Используя
эти
значения
среднего
и
дисперсии
каждого
из
слагаемых
в
сумме
В,
мы
получим
Е[В]
= 100(4) =400,
D[S] = 100(9) = 900.
Необходимая
минимальная
величина
h
фонда
определяется
из
соотношения
р(в:::;
h)
=0,95
или,
что
эквивалентно,
Р
[8
-
Е[8]
~
h - 400] =
О
95.
V
D
(8]
~
ЗО
'
4.2.
Страховые
договоры
с
выплатами
в
момент
смерти
Применяя
нормальную
аппроксимацию
1
),
мы
получаем
2
)
h - 400 =
1645
h
44935
30 "
=,.
103
Замечания.
1.
Разница
между
начальным
капиталом,
равным
449,35,
и
мате
матическим
ожиданием
настоящей
стоимости
всех
платежей,
равным
400,
состав
ляющая
49,35,
является
рисковой
надбавкой
из
гл.
1.
Надбавка
на
одно
лицо
состав
ляет
0,4935,
или
4,935%
на
выплату
размера
1,
или
12,34%
актуарной
настоящей
стоимости.
2.
Этот
пример,
так
же
как
примеры
2.5.2
и
2.5.3,
использует
модель
индиви
дуальных
рисков
и
нормальную
аппроксимацию
распределения
С.в.
В.
в
приме
рах,
относящихся
к
коротким
временным
интервалам,
полные
поступления,
равные
ожидаемым
выплатам
плюс
рисковая
надбавка,
определялись
так,
чтобы
с
боль
шой
вероятностью
превосходить
сумму
выплат.
В
рассмотренном
при
мере
с
боль
шим
интервалом
времени
полные
поступления
плюс
проценты
на
них при
заданной
процентной
ставке
определялись
так,
чтобы
их
хватало
для
покрытия
выплат
по
до
говорам.
Начальный
капитал
в
размере
449,35
покроет
менее
чем
45%
ожидаемых
в
конце
концов
выплат,
равных
1000.
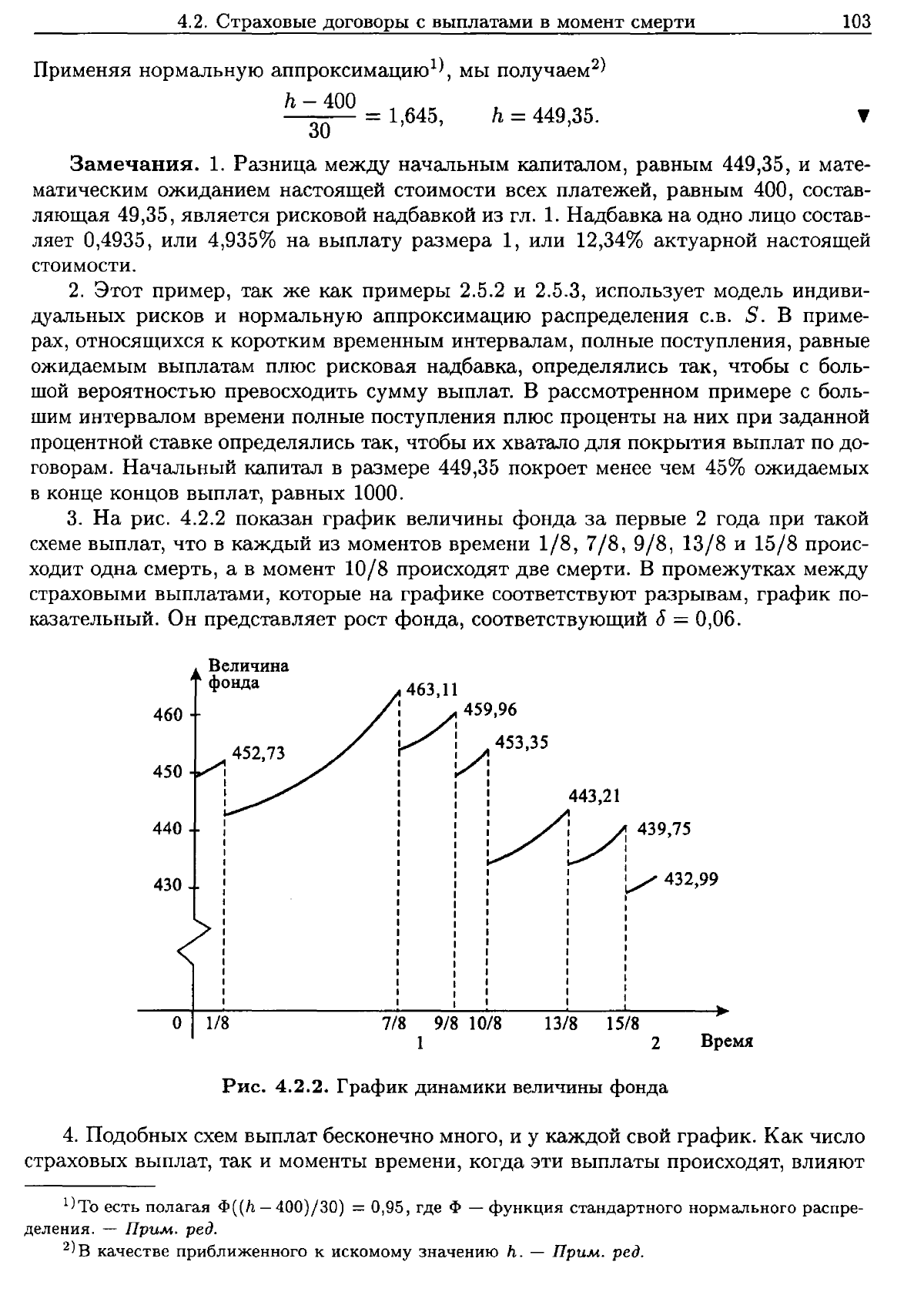
3.
На
рис.
4.2.2
показан
график
величины
фонда
за
первые
2
года
при
такой
схеме
выплат,
что
в
каждый
из
моментов
времени
1/8,7/8,
9/8,
13/8
и
15/8
проис
ходит
одна
смерть, а
в
момент
10/8
происходят
две
смерти.
В
промежутках
между
страховыми
выплатами,
которые
на
графике
соответствуют
разрывам,
график
по
казательныЙ.
Он
представляет
рост
фонда,
соответствующий
д
= 0,06.
Величина
фонда
460
452,73
450
440
430
463.11
459.96
V~45з.З5
443,21
И
·
1439,75
I I
I I
I
V 432,99
I
I
•
•
•
•
•
•
I
I
I
о
1/8
7/8 9/8
10
8
1
13/8 15/8
2
Время
Рис.
4.2.2.
График
динамики
величины
фонда
4.
Подобных
схем
выплат
бесконечно
много, и у
каждой
свой
график.
Как
число
страховых
выплат,
так
и
моменты
времени,
когда
эти
выплаты
происходят,
влияют
l)To
есть
полагая
Ф((h
-
400)/30)
=0,95,
где
Ф
-
функция
стандартного
нормального
распре
деления.
-
Прu,м.
ред.
2)
Б
качестве
приближенного
к
искомому
значению
h.
-
Прu.м.
ред.

104
Гл.
4.
Страхование
жизни
на
фонд.
Например,
если
вместо
схемы,
изображенной
на
рис.
4.2.2,
семь
выплат
произойдут
одновременно
в
самый
первый
момент,
размер
фонда
сразу
же
сокра
тится
до
379,35
и
затем
возрастет
до
427,72
к
концу
второго
года.
Приведенные
примеры
иллюстрируют
три
различные
случайные
составляющие
конструкции
модели
рисков,
а
именно,
произойдет
или
нет
страховая
выплата,
ка
ков
будет
ее
размер
и
в
какое
время
будет
произведена
выплата,
если
она
произой
дет.
В
примере
2.5.2
имелась
лишь
неопределенность,
произойдет
выплата,
или
нет.
В
примере
4.2.2
имелась
неопределенность
лишь
относительно
времени
выплаты.
В
этих
моделях
иные
неопределенности
не
рассматривались.
В
примерах
4.2.1, 4.2.2
и
4.2.3
мы
не
рассматривали
возможность
того,
что
увеличение
капитала
может
про
исходить
за счет
начисления
процентов
снедетерминированной
процентной
ставкой.
4.2.2.
Смешанное
страхование
Страхование
'Н,а
дожитие
'Н,а
СрО'К:
n
лет
предполагает
выплату
по
истечении
n
лет
в
том
и
только
в
том
случае,
когда
страхователь
будет
жив
по
прошествии
n
лет
с
момента
заключения
страхового
договора.
Если
выплачиваемая
сумма
составляет
единицу,
то
b
t
=
{о,
1,
t
~
n,
t > n,
t
~
о,
Z =
{о,
v
n
,
т
~n,
Т>n.
Единственным
элементом
неопределенности
в
страховании
на
дожитие
является
факт,
произойдет
или
не
произойдет
страховая
выплата.
Размер
и
время
произве
дения
выплаты
при
условии,
что
выплата
произойдет,
определены
заранее.
В
выра
жении
Z =
vny
величина
У
является
индикатором
события
«дожитие
до
возраста
х
+n».
Эта
величина
принимает
значение
1,
если
страхователь
доживет
до
возрас
та
х
+
n,
и
значение
О
в
противном
случае.
Для
обозначения
актуарной
настоящей
стоимости
страхования
на
дожитие
на
срок
n
лет
имеется
два
символа.
В
страховом
контексте
это
величина
Ax:fu,
Мы
увидим
в
следующей
главе,
что
в
контексте
анну
итетов
та
же
величина
обозначается
через
nЕх.
Это
разграничение
выполняется
не
слишком
строго.
Читатель
должен
быть
готов к
любой
из
форм
записи,
Ах:iи
=E[Z] =v
n
Е[У]
=v
n
nРх
и
D[
Z]
=v
2n
D[Y] =v
2n
nРх
nqx =
2А
х
:iи
-
(А
х
:iи)2.
(4.2.9)
Смешан/ное
страхова'Н,ие
'На
СрО'К:
n
лет
предполагает
выплату
либо
по
смерти
страхователя,
либо
по
дожитии
им
до
истечения
n-летнего
срока,
в
зависимости
от
того,
что
случится
раньше.
Если
размер
выплаты
-
единица
и
если
выплаты
на
случай
смерти
производятся
в
момент
смерти,
то
b
t
=l,
t~O,
Vt={v
t
,
t~n,
z={v
T
,
T~n,
v
n
,
t > n, v
n
,
Т
> n.
Актуарная
настоящая
стоимость
обозначается
через
А
х
:
m
.
Поскольку
для
смешан
ного
страхования
b
t
= 1,
по
правилу
моментов
мы
имеем
Е[Zj]@б
=
Е[Z]@jб.
Кроме
того,
(4.2.10)

4.2.
Страховые
договоры
с
выплатами
в
момент
смерти
105
(4.2.11)
(4.2.13)
(4.2.12)
Такое
страхование
можно
рассматривать
как
комбинацию
страхования
на
случай
смерти
на
срок
n
лет
и
страхования
на
дожитие
на
срок
n лет -
в
каждом
случае
с
выплатой
размера
1.
Пусть
Z1,
Z2
И
Zз
-
случайные
величины,
обозначающие
настоящую
стоимость
договора
срочного
страхования,
страхования
на
дожитие
и
смешанного
страхования
соответственно,
в
каждом
из
которых
страховая
выплата
производится
в
момент
смерти
лица
(х).
Из
предыдущих
определений
мы
имеем
Z1
=
{v
T
,
Т
~
N,
Z2
=
{vO~
т
~
N,
ZЗ
=
{v:,
т
~
n,
О,
т
> n, ,
Т
> n,
v,
Т
> n.
Отсюда
следует,
что
Zз
=
Z1
+
Z2,
и,
беря
математические
ожидания
от
обеих
частей,
мы
получаем
-
-1
1
А
х
:
nl
=
А
х
:
nl
+
А
х
:
m
,
С
помощью
равенства
(4.2.11)
мы
можем
также
найти
D(Zз]:
D[Zз]
= D[Zl] +
D(Z2]
+2
COV(Zl'
Z2),
Воспользовавшись
формулой
COV(Z1,
Z2)
=
E[Z1Z2]
-
E[Z1]E[Z2]
(4.2.14)
и
заметив,
что
Z1
Z2
=
О
для
всех
Т,
мы
получим
-1
1
COV(Z1,
Z2)
=
-E[Zl]
E[Z2]
=
-Ах:mА
х
:
nl
.
(4.2.15)
Подстановка
формул
(4.2.5), (4.2.9)
и
(4.2.15)
в
(4.2.13)
приводит
к
формуле
для
D[Zз]
в
терминах
актуарной
настоящей
стоимости
для
страхования
на
случай
смер
ти
на
срок
n лет и
для
страхования
на дожитие.
Поскольку
актуарные
настоящие
стоимости
положительны,
величина
COV(Zl,
Z2)
отрицательна.
Это
можно
было
понять
заранее,
поскольку
одна
вели
чина
из
пары
Z1
и
Z2
всегда
нулевая,
а
другая
положительная.
С
другой
стороны,
коэффициент
корреляции
между
с.в.
ZI
и
Z2
не
равен
~1,
поскольку
эти
величины
не
связаны
линейной
зависимостью.
Вспомним
упр.
1.23(с).
4.2.3.
Отсроченное
страхование
Страхова'Н.ие,
отсро-ч,е'Н.'Ное
'На
т
лет,
предполагает
выплату
сразу
после
смерти
страхователя
только
в
том
случае,
если
он
умрет
не
раньше,
чем
через
т
лет
после
заключения
страхового
договора.
Выплачиваемая
сумма
и
срок,
на
который
заклю
чен
договор,
могут
быть
любыми
из
обсуждавшихея
выше.
Например,
бессрочное
страхование
на
случай
смерти,
отсроченное
на
т
лет,
с
выплатой
в
момент
смерти
страхователя
суммы,
равной
единице,
определяется
соотношениями
b
t
=
{1,
О,
t >
т,
t
~
т,
_ t
vt
- v , t >
О,
Z =
{v
T
,
О,
Т>т,
T~m.
['"
v'
,р,
JL,
(t) dt. (4.2.16)
Пример
4.2.4.
Рассмотрим
бессрочное
страхование
на
случай
смерти,
отсро
ченное
на
5
лет,
с
выплатой
в
момент
смерти
лица
(х).
Интенсивность
смерти
J-L
Актуарная
настоящая
стоимость
такого
страхования
обозначается
через
ml
Ах
и
рав
на

106
Гл.
4.
Страхование
жизни
для
этого
лица
равна
0,04.
При
б
= 0,10
для
распределения
настоящей
стоимости
выплаты
(а)
подсчитаем
математическое
ожидание,
(Ь)
подсчитаем
дисперсию,
(с)
выпишем
функцию
распределения,
(d)
подсчитаем
медиану
~~5.
Решение.
(а)
Для
произвольных
1-"
и
б
5jAx
=
(=10
е-бtе-J.tt
J.t
dt =
J.t
е-5(J.t+б).
15
J.t+б
Поэтому
для
J.t
= 0,04
и
б
= 0,10
51
Ах
= (2/7)
е-
О
,7
=0,1419.
(Ь)
По
правилу
моментов
D(Z] = 0,04
е-
5
(D,О4+0,20)
_
~
e-
1
,4 = 00301.
0,04
+0,20
49'
(с)
Как
и
в
случае
бессрочного
страхования
на
случай
смерти,
решение
выте
кает из
графика
связи
между
С.в.
Z
и
Т.
ДЛЯ
отсроченного
на
т
лет
договора
страхования
этот
график
приведен
на
рис.
4.2.3.
z
v
m
--------
z
о
т
lnz
lп
v
т
Рис.
4.2.3.
Связь
между
с.в.
Z
и
Т
для
отсроченного
бессрочного
страхования
на
случай
смерти
Хотя
Т
-
непрерывная
случайная
величина,
Z
является
случайной
величиной
смешанного
типа
со
«сгустком»
вероятностной
массы
в
точке
О,
поскольку
событие
Z =
О
соответствует
событию
Т
~
т.
При
общих
предположениях
о
смертности
и
при
постоянной
интенсивности
на
числения
процента
мы
имеем:
•
для
события
Z =
О
Fz(O) =
Р(Т
~
т)
=
Рт(т);
(4.2.17)
•
для
0<
z < v
m
Fz(z)
=
P(Z
~
z)
=
P(Z
=
О)
+
Р(О
<Z
~
z)
=
Р(Т
~
т)
+
Р(О
<v
T
~
z)
=
Р(Т
~
т)
+
Р(Т
> ln
z/
ln
v)
=
Рт(т)
+1 - FT(ln
z/
lnv); (4.2.18)
•
для
z > v
m
Fz(z)
= 1. (4.2.19)
в
этом
примере
отсроченного
на
5
лет
бессрочного
страхования
на
случай
смерти
с
J.t
= 0,04
и
б
= 0,10

4.2.
Страховые
договоры
с
выплатами
в
момент
смерти
•
в
силу
формулы
(4.2.17)
Fz(O) =
Рт(5)
= 1 -
е-О,2
=0,1813;
•
согласно
формуле
(4.2.18)
для
О
< z < v
5
Fz(O) =
Рт(5)
+1 -
Р
Т
(
l~Zl)
=
1-
е-О,2
+
zO,04/0,10
= 0,1813 +
zO,4;
,
•
по
формуле
(4.2.19)
для
z > v
5
Fz(z)
=
1.
График
этой
функции
распределения
приведен
на
рис.
4.2.4.
Рис.
4.2.4.
Функция
распределения
С.В.
Z
107
(4.2.20)
(d)
Из
рис.
4.2.4
или
из
формулы
(4.2.20)
мы
получаем,
что
медиана
является
решением
уравнения
0,5 = 0,1813 +
zO,4.
Таким
образом,
~~,5
=0,0573.
у
Замечания.
1.
В
этом
примере
наибольшее
значение
С.В.
Z,
при
котором
плот
ность
распределения
С.в.
Z
ненулевая,
равно
е-О,1(5)
= 0,6065,
что
соответствует
значению
Т
= 5.
2.
Распределение
С.в.
Z
в
этом
примере
асимметрично
и
сильно
смещено
вправо.
Его
полная
масса
сосредоточена
в
интервале
[О,
0,6065],
его
среднее
равно
0,1419,
но
его
медиана
равна
всего
лишь
0,0573.
Эта
асимметрия
со
смещением
в
сторону
больших
положительных
значений
является
типичной
для
многих
распределений
величин
страховых
выплат
во
всех
областях
страхования.
4.2.4.
Страхование
с
изменяющимися
выплатами
Общую
модель,
определяемую
формулой
(4.2.1),
можно
использовать
в
боль
шинстве
приложений.
Мы
использовали
ее
применительно
к
договорам
страхова
ния
жизни
с
постоянными
выплатами.
Она
может
также
при
меняться
к
договорам
страхования,
в
которых
величина
выплат
на
случай
смерти
либо
возрастает,
либо
убывает
в
арифметической
прогрессии
в
течение
всего
срока
действия
страхового
договора
или
части
этого
срока.
Такой
страховой
продукт
часто предлагается
в ка
честве
дополнительного
покрытия,
когда
основной
страховой
договор
обеспечивает

108
Гл.
4.
Страхование
жизни
возврат
периодически
выплачиваемых
премий
в
момент
смерти
или
когда
аннуи
тет
содержит
гарантию
того,
что
выплаты
будут
соответствовать
оговоренной
в
нем
начальной
премии.
Вессро'Чное
страхование
на
слу'Чай
с,м,ерти
с
ежегодно
увел'U'Чива70щейся
стра
ховой
въtnлатой,
согласно
которому
выплачивается
1
в
момент
смерти
в
течение
первого
года,
2
в
момент
смерти
в
течение
второго
года
и
так
далее,
характеризует
ся
следующими
функциями:
b
t
= lt + 1J, t
~
О,
Z=lT+IJv
T
,
T~O,
где
l J
обозначает
целую
часть
числа.
Актуарная
настоящая
стоимость
для
такого
страхования
обозначается
через
(1
А)х
и
равна
E[Z]
=
100
Lt
+1
Jv'
,Р.
JL.(t) dt.
в
отличие
от
случая
страхования
со
страховыми
выплатами,
равными
О
и
1,
при
скорректированной
интенсивности
начисления
процента
моменты
высшего
порядка
не
равны
актуарной
настоящей
стоимости.
Эти
моменты
могут
быть
вычислены
непосредственно
с
помощью
их
определений.
Увеличения
страховой
выплаты,
оговоренные
в
страховом
договоре,
могут
про
исходить
чаще
или
реже,
чем
один
раз
в
год.
Для
бессро'Чного
страхования
на
слу'Чай
смерти
со
страховой
въtnлатоu,
увелu'Чuва70щейс,я,
т
раз
в
год,
выплаты
составля
ют
11т
в
момент
смерти
в
течение
первого
из
т
интервалов,
на
которые
разбит
год,
2/
m
в
момент
смерти
в
течение второго
такого
интервала
и
т.
Д.,
увеличиваясь
на
11т
в
каждый
последующий
интервал.
Для
такого
страхования
жизни
b
t
= L
tm
+1J, _ t
t
~
О,
vt
- V ,
m
Актуарная
настоящая
стоимость
-
это
t
~
О,
т
~
О.
Предельный
случай
при
т
-+
00
для
бессрочного
страхования
на
случай
смерти
со
страховой
выплатой,
увеличивающейся
т
раз
в
год,
является
страхованием
с
выплатой
суммы
t
в
момент
смерти
t.
Соответствующие
функции
имеют
вид
b
t
:::::
t, t
~
О,
Vt
=v
t
,
t
~
О,
Z =
Tv
T
,
Т
~
О.
в
этом
случае
актуарная
настоящая
стоимость
обозначается
через
(1
А)х.
Такое
бессрочное
страхование
на
случай
смерти
с
непрерывным
увеличением
размера
выплаты
эквивалентно
множеству
договоров
бессрочного
отсроченного
стра
хования
на
случай
смерти
с
постоянными
выплатами.
Эта
эквивалентность
показана
графически
на
рис.
4.2.5,
где
область
между
прямой
b
t
=t
и
осью
t
представляет
до
говоры
страхования
по
всему
времени
предстоящей
жизни.
Если
объединить
инфи
нитезимальные
области
l
)
по
вертикали
для
фиксированного
t,
получается
выплата
в
момент
t.
Если
объединить
их по
горизонтали
для
фиксированного
s,
то
полу
чится бессрочное
страхование
на
случай
смерти,
отсроченное
на
s
лет,
при
размере
выплаты
ds.
l)Области
сбесконечно
малой.
ширины.
-
Прu.м..
ред.

4.2.
Страховые
договоры
с
выплатами
в
момент
смерти
109
s
dt
=ds
t
Рис.
4.2.5.
Страхование
с
непрерывно
увеличивающейся
выплатой
Из
этой
эквивалентности
следует,
что
актуарные
настоящие
стоимости
для
ука
занныХ'~трахований
равны.
Их
равенство
может
быть
доказано
также
следующим
образом."~
По
опре~ению
(l
А)х
=
[Ю
t
v'
,Рх
f.Lx(t)
dt,
И,
интерпретируя
t
под знаком
интеграла
как
интеграл
от
нуля
до
t
на
рис.
4.2.5,
мы
имеем
(Н)х
=
100
(1
!
ds)
v
t
tPx
f.Lx
(t) dt.
Если
мы
изменим
порядок
интегрирования
и
для
каждого
значения
s
проинтегри
руем
по
t
от
s
дО
Х,
то
получим,
согласно
формуле
(4.2.16),
(l
А)х
=
100
/.00
v'
tPx
f.Lx
(t)
dt
ds
=
100
slA
x
ds.
Если
по
такому
договору
с
увеличением
размера
выплаты
т
раз
в
год
выплата
на
случай
смерти
производится
только
в
случае,
если
смерть
наступила
не
позд
нее,
чем
через
n
лет
с
момента
заключения
договора,
то
этот
договор
называется
договором
страхования
иа
слу'Чай
смерти
на
сро",
n
лет
со
страховой
въtnлатоu,
увелu'Чuвающейся
т
раз
в
год.
В
некотором
смысле
противоположными
к
договорам
страхования
на
случай
смерти
сроком
на
n
лет
с
ежегодно
увеличивающейся
выплатой
являются
договоры
страхованuя
на
слу'Чай
смерти
на
сро'К
n
лет
с
ежегодно
умен.'ЬшающеЙся
стра
ховой
выплатой,
согласно
которым
в
момент
смерти,
произошедшей
в
первый
год,
выплачивается
сумма
n,
в
момент
смерти,
произошедшей
во
второй
год
-
сумма
n - 1
и
т.
д.,
так
что
выплата
становится
нулевой
по
окончании
n-го
года.
Такому
договору
соответствуют
функции
b
t
=
{n
-
LtJ,
о,
t
~
n,
t > n,
t
~
О,
z =
{vT(n
-
LTJ),
О,
T~n,
Т>n.
fj<;
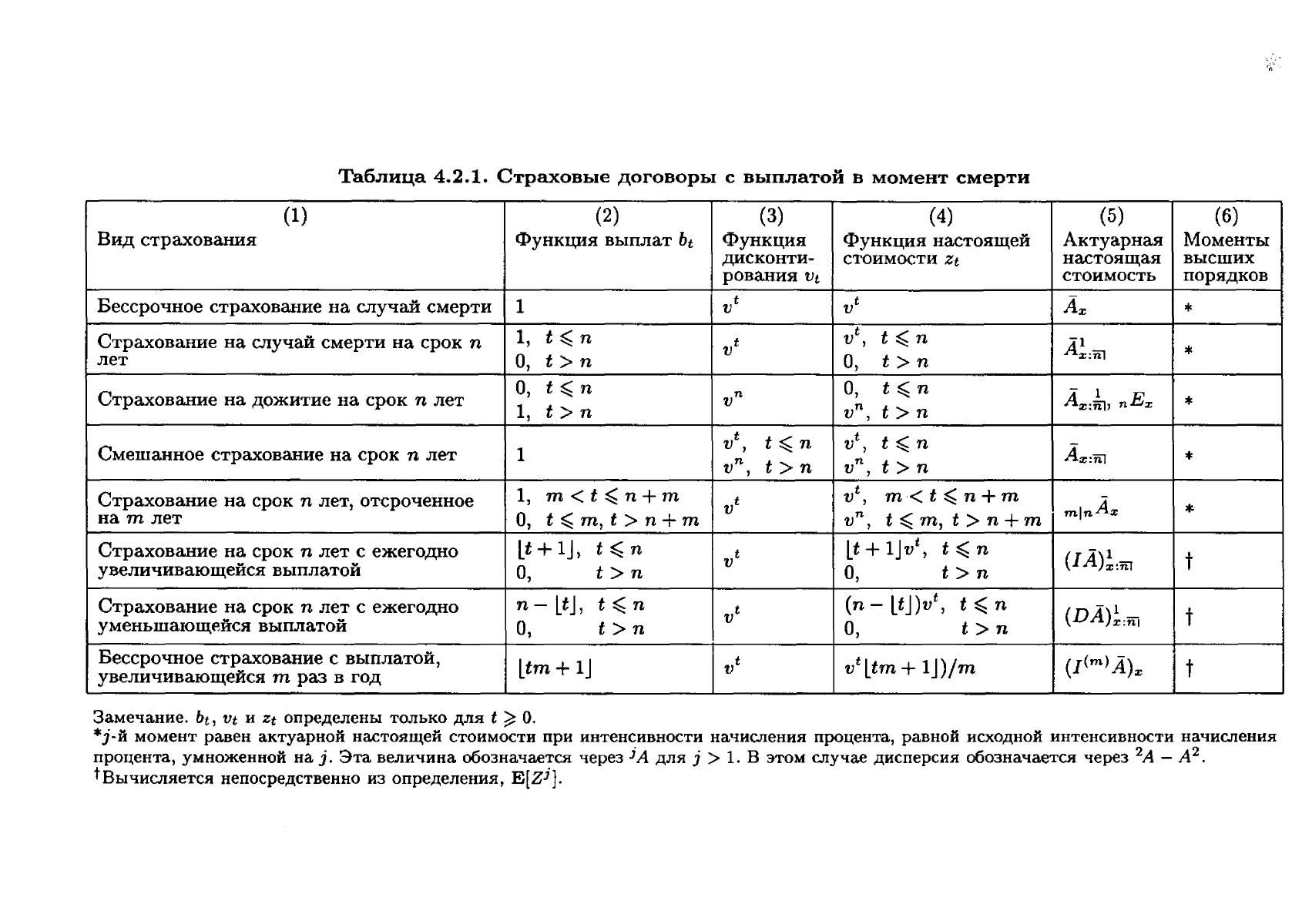
Таблица
4.2.1.
Страховые
договоры
с
выплатой
в
момент
смерти
(1)
(2)
(3)
(4)
(5)
(6)
Вид
страхования
Функция
выплат
b
t
Функция
Функция
настоящей
Актуарная
Моменты
дИсконти-
стоимости
Zt
настоящая
высших
рования
Vt
стоимость
порядков
Бессрочное
страхование
на
случай
смерти
1 v
t
v
t
Ах
*
Страхование
на
случай
смерти
на
срок
n
1,
t
~
n
v
t
v
t
t~n
-1
,
А
ж
:
iil
*
лет
О,
t>n
О,
t>n
Страхование
на
дожитие
на
срок
n
лет
О,
t~n
v
n
О,
t~n
- 1
А
ж
:
iil
,
nЕ
х
*
1,
t > n
v
n
,
t > n
t
t
~
n
v
t
t
~
n
Смешанное
страхование
на
срок
n
лет
1
v,
,
А
ж
:
iil
*
v
n
t>n
v
n
,
t > n
,
Страхование
на
срок
n
лет,
отсроченное
1,
m<t~n+m
v
t
v
t
m<t~n+m
mln
Аж
,
*
на
m
лет
О,
t
~
т,
t > n
+т
v
n
t
~
т,
t > n
+т
,
Страхование
на
срок
n
лет
с
ежегодНО
Lt+lJ,
t~n
v
t
Lt+lJv
t
,
t
~
n
(IA)~:nт
t
увеличивающейся
выплатой
О,
t > n
О,
t > n
Страхование
на
срок
n
лет
с
ежегодНО
n-
LtJ,
t~n
v
t
(n
-ltJ)v
t
,
t
~
n
(DA)~:n,
t
уменьшающР.Йся
выплатой
О,
t>n
О,
t > n
Бессрочное
страхование
с
выплатой,
ltm
+ lJ
v
t
vtltm+
lJ)/m
(I(m)
А)х
t
увеличивающейся
m
раз в
год
Замечание.
bt,
Vt
и
Zt
определены
только
для
t
~
О.
*j-й
момент
равен
актуарной
настоящей
стоимости
при
интенсивности
начисления
процента,
равной
исходной
интенсивности
начисления
процента,
умноженной
на
j.
Эта
величина
обозначается
через
j
А
для
j > 1.
В
этом
случае
дисперсия
обозначается
через
2
А
-
А
2.
tВычисляется
непосредственно
из
определения,
E[zj].

4.3.
Страховые
выплаты,
производимые
в
конце
года
смерти
Актуарная
настоящая
стоимость
такого
договора
страхования
-
это
111
- 1
{n
t
(DA)x:nl =
Jo
V (n -
ltJ)
tPx
J.Lx(t)
dt.
Этот
договор
является
противоположным
к
договору
страхования
на
случай
смерти
сроком
на
n
лет
с
ежегодно
увеличивающейся
выплатой
в
том
смысле,
что
сумма
их
функций
выплат
является
постоянной
и
равной
n +1
для
срока
в
n
лет.
В
табл.
4.2.1
приводится
сводка
результатов
настоящего
раздела.
В
первом
столб
це
содержится
название
страхового
плана,
далее
даются
функции
выплат
и
дис
контирования,
которые
определяются
в
терминах
продолжительности
предстоящей
жизни
страхователя
на
момент
заключения
договора
страхования.
Затем
указыва
ется
функция
настоящей
стоимости,
которая
всегда
получается
как
произведение
двух
предыдущих
функций.
В
пятом
столбце
представлено
обозначение
для
акту
арной
настоящей
стоимости,
принятое
в
Международной
системе
актуарных
обо
значений.
Символ
в
последнем
столбце,
отсылающий
к
подстрочному
примечанию
к
этой
таблице,
указывает,
может
ли
для
вычисления
моментов
высших
порядков
применяться
правило
моментов.
4.3.
Страховые
выплаты,
производимые
в
конце
года
смерти
В
предыдущем
разделе
мы
рассматривали
модели
страхования
жизни,
в
кото
рых
выплаты
производились
в
момент
смерти.
На
практике
большинство
выплат
производится
в
момент
смерти,
так
что
проценты
начисляются
до
того
момента,
как
выплаты
будут
реально
произведены.
Эти
модели
формулировались
в
терминах
с.в.
Т,
продолжительности
предстоящей
жизни
страхователя
на
момент
заключе
ния
страхового
договора.
Но
в
большинстве
практических
приложений
страхования
жизни
самой
точной
информацией
о
распределении
С.в.
Т
является
таблица
смерт
ности,
в
которой
информация
дискретизирована.
На
самом
деле
это
-
информация
о
с.в.
К,
пошаговой
продолжительности
предстоящей
жизни
страхователя
в
момент
заключения
договора
страхования,
которая
является
функцией
от
С.в.
Т.
В
этом
и
в
следующем
разделе
мы
устраняем
этот
недочет,
строя
модели
страхования
жизни,
в
которых
величина
и
время
выплат
на
случай
смерти
зависят
только
от
числа
пол
ных
лет,
прожитых
страхователем
с
момента
заключения
договора
до
момента
его
смерти.
Мы
будем
называть
такие
договоры
страхования
договорами
с
вЪtnлата.ми,
осуществляемыми
в
'Х:он:це
года
смерти.
Наша
модель
формулируется
в
терминах
пошаговой
продолжительности
пред
стоящей
жизни
страхователя.
Функция
выплат
b
k
+
1
и
функция
дисконтирования
Vk+l
соответственно
являются
величиной
выплаты
и
коэффициентом
дисконтиро
вания,
относящимися
к
периоду
от
момента
произведения
выплаты
назад
до
момента
заключения
договора,
если
пошаговая
продолжительность
жизни
страхователя
рав
на
k,
т.
е.
он
умирает
на
k +
1-м
году
С
момента
заключения
страхового
договора.
Настоящая,
на
момент
заключения
договора,
стоимость
этой
страховой
выплаты,
обозначаемая
через
Zk+l,
определяется
формулой
(4.3.1)
Если
исходить
из
момента
заключения
договора,
то
номер
страхового
года,
когда
происходит
смерть,
равен
1
плюс
пошаговая
продолжительность
предстоящей
жиз
ни
страхователя
К.
Это
случайная
величина,
определенная
в
разд.
3.2.3.
Как
и
в
