Афанасьев А.А. Математические основы теории систем управления
Подождите немного. Документ загружается.

Министерство общего и профессионального образования Российской
Федерации
Чувашский государственный университет имени И.Н. Ульянова
А.А.Афанасьев
МАТЕМАТИЧЕСКИЕ ОСНОВЫ
ТЕОРИИ СИСТЕМ УПРАВЛЕНИЯ
РАЗДЕЛ ПЕРВЫЙ
Уравнения состояния систем
автоматического управления
Учебное пособие
Чебоксары 1996
2
УДК 517(075)
Рецензенты: кафедра автоматики Мордовского государственного
университета им. Н.П. Огарева ( зав. кафедрой, проф. И.Г. Учайкин),
д-р техн. наук, проф. Ю.П. Сонин
Афанасьев А.А. Математические основы теории систем управления:
Раздел первый. Уравнения состояния систем автоматического
управления: Учеб. пособие. Чуваш. ун-т, Чебоксары: 1996. 168 с.
Рассматриваются аналитические, численно-аналитические и численные
методы решения линейных ( с постоянной и нестационарной матрицей) и
нелинейных уравнений состояния, представленных в нормальной форме Коши.
Аналитические решения находятся на основе аппарата матричных функций и
теории проекторов. Анализируются проблемы устойчивости различных
методов численного интегрирования и жесткости уравнений состояния. С
помощью уравнений состояния и конечных уравнений рассматриваются
некоторые методы идентификации объектов управления.
Для студентов, обучающихся по направлению “Автоматизация и
управление”, а также по направлениям “Электротехника, электромеханика и
электротехнологии”, “Электроэнергетика” и ряду других в области технических
наук.
Утверждено Редакционно-издательским советом университета
Ответственный редактор: д-р техн. наук, проф. Г.А. Белов

ВВЕДЕНИЕ
При расcмотрении систем автоматического управления (САУ) возможны
два подхода к их математическому описанию. Первый традиционный подход
сводится к расчленению САУ на отдельные звенья, составлению структурной
схемы, определению передаточных функций, как звеньев, так и всего канала
между точками входа и выхода.
Если через
)(
t
x
и
)(
t
q
обозначить соответственно выходную
переменную и входное воздействие, то в конечном итоге САУ описывается
дифференциальным уравнением n
- го порядка
),(
1
)(
1
1
)(
0
)(
1
)(
1
1
)(
0
tq
m
b
m
td
tq
m
d
b
m
td
tg
m
d
btx
n
a
n
td
tx
n
d
a
n
td
tx
n
d
a
++
−
−
+
+=++
−
−
+
K
K
(В.1)
которому в изображениях по Лапласу можно придать вид:
Рис. В. 1
,
)()1
11
1
()()1
11
1
(
pq
m
p
m
m
m
p
m
m
kpx
n
p
n
n
T
n
p
n
n
T
++
−−
−
+=++
−−
−
+ KK
ττ
где
n
a
m
b
k
m
b
b
m
m
m
b
b
m
m
n
a
a
n
n
T
n
a
a
n
n
T
dt
d
p ==
−
−
==
−
−
== ,,
1
1
1
,
0
,,
1
1
1
,
0
, KK
ττ
-
коэффициент усиления; параметры
ji
T
τ
, имеют размерность времени и
называются постоянными времени.
Отношение выходного сигнала
)(
p
x
к входному )(
p
q
)(
называется
передаточной функцией САУ и обычно обозначается
p
W
3

1
11
1
)1
11
1
(
)(
)(
)(
+
−−
−
+
+
−−
−
+
==
K
K
n
p
n
n
T
n
p
n
n
T
m
p
m
m
m
p
m
m
k
pq
px
pW
ττ
.
Уравнение (В.1) соответствует линейной скалярной системе с одним
входом и одним выходом (рис. В.1).
Второй подход заключается в составлении системы дифференциальных
уравнений первого порядка в нормальной форме, т. е. разрешенных
относительно производной
.)](,)([
)(
tqtxf
td
txd
= (B.2)
Переменные
=jtx
j
()(
1, 2 ..., ), являющиеся координатами вектора n
Т
])(t)(
2
)(
1
[)(
n
xtxtxtx K=
и фигурирующие в уравнении (В.2) под знаком
производной, называются переменными состояния. Они характеризуют
внутреннее динамическое состояние САУ и аналогичны обобщенным
координатам в классической механике. Переменные (
i
q
t ) (i = 1, 2 ,... ,
m
)
являются координатами вектора входного воздействия
)]()()()(
21
tqtqtqtq
m
K[= .
Современные САУ являются фактически многоканальными. Размерность
вектора
)(tq совпадает с количеством входных каналов САУ.
Количество выходных каналов САУ не зависит от числа переменых
состояния и диктуется ее функциональным назначением. Выходными
переменными могут быть некоторые (или все) переменные состояния и
другие переменные, представляющие технологический и информационный
интерес. Вектор выходных переменных
T
21
])()()([)( tytytyty
r
K= яляется в общем
случае некоторой функцией векторов состояния и внешних воздействий. Эта
функция задается конечным уравнением вида
)].(,)([)( tqtxty
ψ
= (B.3)
Множества значений векторов в каждый момент времени t образуют
пространства соответственно состояния, входа и выхода САУ.
При исследовании САУ фигурируют два типа задач.
К первому типу относятся задачи анализа, когда требуется определить
характеристики заданной системы.
4

Ко второму типу - задачи синтеза, когда требуется сформировать систему
с заданными характеристиками.
Методы анализа и синтеза систем управления, использующие
рассматриваемый способ описания поведения системы, принято называть
методами пространства (переменных) состояния [5, 18]. Этот подход лежит в
основе современной теории управления. Он позволяет применить эффективные
методы оптимизации движения САУ в пространстве возможных состояний:
вариационное исчисление (Л. Эйлер), принцип максимума (Л.С. Понтрягин),
динамическое программирование (Р. Беллман) и др.
Векторному уравнению (B.2) соответствует блок-схема САУ на рис.
В.2,а.
а) б)
Рис. В. 2
Блок-схему можно упростить, если условиться изображать векторы
двойной линией (рис. В.2,б).
Для линейных систем уравнения (B.2), (В.3) примут вид
),()]([)()]([
)(
tqtBtxtA
td
txd
+= (B.4)
[ ]
),()()()]([)( tqtDtxtCty += (B.5)
где [ ])(
t
A
- квадратная параметрическая матрица системы размером n,
[ ])(
t
B
- входная матрица системы размером mn× ,
)]([
t
C
- выходная матрица системы размером n
r
× ,
)]([
t
D - проходная матрица размером m
r
× .
5
Для линейных стационарных систем указанные матрицы будут
постоянными.
Переменные состояния (j = 1 ,2 , ... ,n,) для данной системы могут
выбираться неоднозначно [5]. При расчете оптимальных САУ целесообразно
координаты вектора состояния
)(tx
j
)(tx выбирать такими, чтобы их можно было
непосредственно наблюдать и измерять.
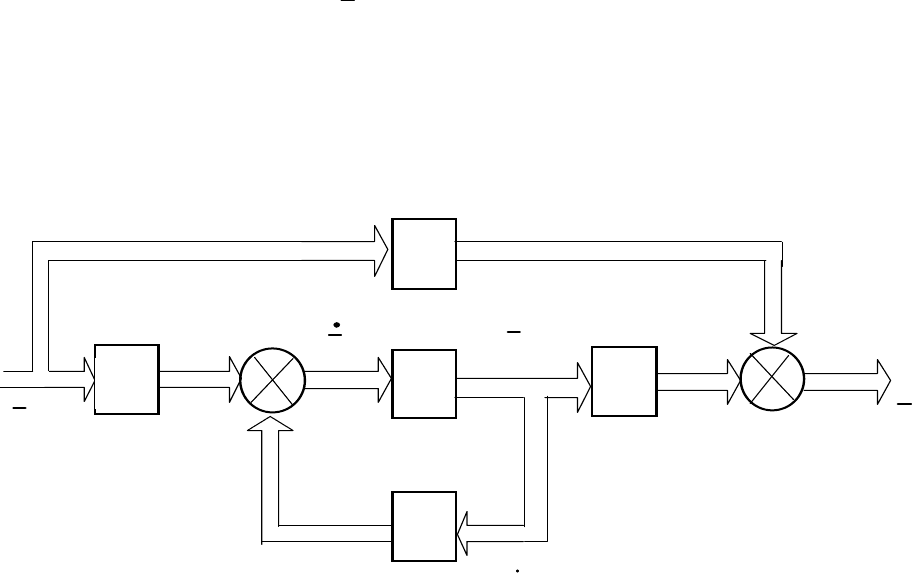
Структурные схемы непрерывных систем в переменных состояния
совпадают со схемами моделирования этих систем на аналоговых
вычислительных машинах. Уравнениям (В.4) и (B.5) будет соответствовать
структурная схема, представленная на рис. В.3.
Рис. B.3
D(t )
B(t)
A
(t)
C(t )
∫
x
x
g
y
Для дискретных САУ дифференциальное уравнение (В.4) заменяется
разностным, а интеграл на рис. В.3 - элементом памяти.
ПРИМЕР В.1.
Рассмотрим применение метода переменных состояния для
математического описания электромеханической следящей системы,
показанной на рис. В.4.
В этой системе с управлением по производной имеются два
тахогенератора (ТГ1 и ТГ2), вырабатывающие сигналы, пропорциональные
производным от угловых координат ведущей (
)/
00
tdd
ϑ
=Ω
и ведомой
(
t
dd
/
ϑ
=Ω ) осей вращения (I и II). Разность этих сигналов (напряжение U
1
)
предназначена для стабилизации следящей системы. Как видно из рис. B.4,
система содержит обратные связи по углу поворота, скорости вращения и току
якоря двигателя.
6
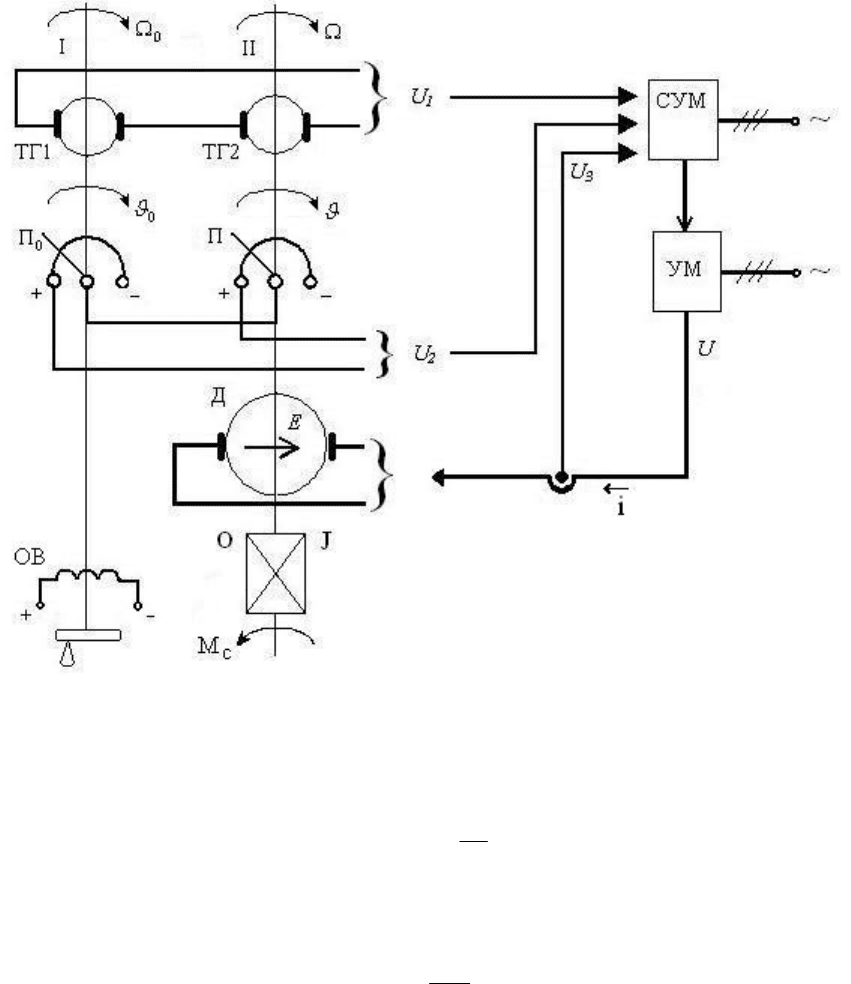
Для электродвигателя постоянного тока независимого возбуждения ( Д)
справедливы уравнения равновесия напряжения цепи якоря
Рис. В. 4
,EiR
td
id
LU ++= (В.6)
равновесия моментов на ведомой оси
c
MM
d
t
d
J −=
Ω
, (B.7)
где
ik
M
=
- вращающий момент двигателя, (B.8)
Ω= cM
c
- момент сопротивления механизма (объекта (B.9)
управления (O)),
Ω= k
E
- ЭДС вращения двигателя. (В.10)
Уравнениям (В.6), (B.7), с учетом (B.8) - (B.10), можно придать вид:
7
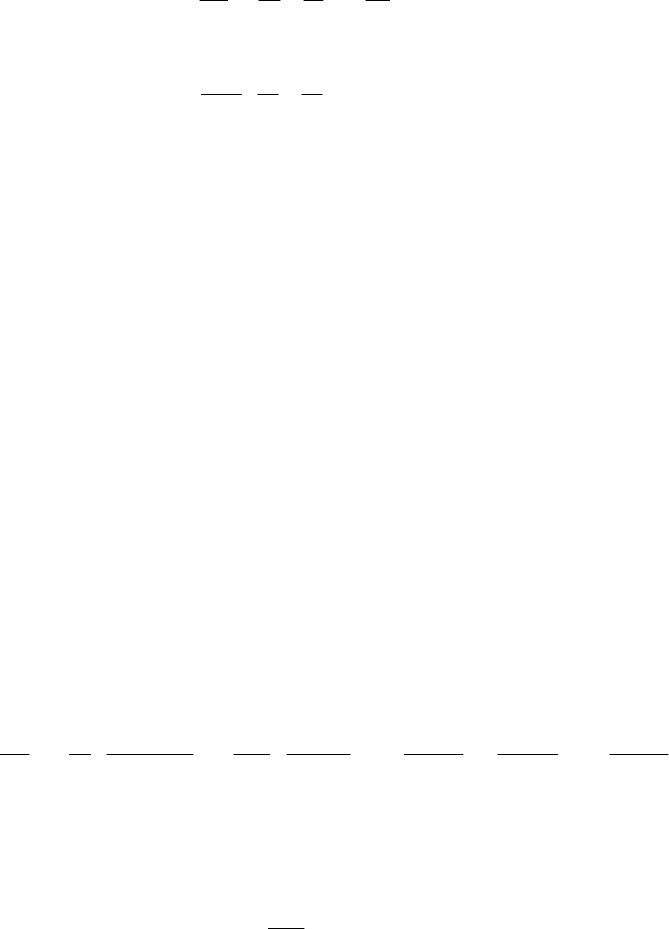
L
U
L
k
i
L
R
td
id
+Ω−−=
, (B.11)
Ω−=
Ω
J
c
i
J
k
td
d
. (В.12)
Выходное напряжение усилителя мощности (УМ)
),UU(UkU
321
++=
M
(B.13)
)(
0T1
Ω−Ω=kU
, (B.14)
)(kU
02
ϑ
ϑ
−=
•
, (B.15)
iRkU
–03
−=
, (В.16)
где
U
1
,U
2
,
U
3
- входные сигналы системы управления усилителя мощности
(СУМ) ,
R
ш
- сопротивление шунта в цепи якоря двигателя.
После подстановки (B.13) - (B.16) в уравнение (B
.
11) получим
−Ω+−+−= )()(
L
kk
L
k
i
L
Rkk
L
R
td
id
TMM
c0M
00
L
kk
L
kk
L
kk
ϑϑ
пMTMпM
+Ω+
(B.17)
К уравнениям (В17), (B.12) следует добавить уравнение для скорости
вращения ведомого вала
Ω=
td
d
ϑ
. (В.18)
Систему из трех уравнений (B.12) ,(В.17) и (B.18) представим в векторно-
матричном виде
8

+
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
Ω
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−+−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
Ω
ϑϑ
i
J
c
J
k
L
kk
L
kk
L
k
L
Rkk
L
R
i
td
d
c
110
0
пMTM
0M
)(
⎥
⎦
⎤
⎢
⎣
⎡
Ω
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
0
0
M
TM
0
0
0
0
ϑ
L
kk
L
kk
п
.
(B.19)
Введем обозначения:
ϑ
=Ω==
321
,,
xxix
- координаты вектора
состояния
x
;
LkkaLkkkaLRkkRa
/,/)(,/)(
1312щoc11
ΠΜΤΜΜ
−=+−=+−=
,1,/,/
322221
=−== aJcaJka
0
333123
=== aaa
-
коэффициенты параметрической матрицы [
А
] размером 3 3;
×
,
Lkkb
/
11
ΤΜ
= Lkkb
/
12
ΠΜ
=
, 0
32312221
==== bbbb
-
коэффициенты входной матрицы [В] размером 3
×
2;
,
01
Ω=q
02
ϑ
=q
- координаты входного вектора
q
.
В результате уравнение (B.19) можно записать в стандартной векторно-
матричной форме
qBxA
d
t
xd
][][ += , (В.20)
где
Τ
= ][
321
xxxx ,
Τ
= ][
21
qqq ,
, .
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
0a0
0aa
aaa
A
32
2221
131211
][
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
0
0
b
0
0
b
B
1211
][
9

Рис. В.5
Соответствующая структурная схема в переменных состояния (рис. В.5)
составлена по уравнению (B.20), записанному в скалярной форме:
2121113132121111
qbqbxaxaxax ++++=
&
,
2221212
xaxax +=
&
,
.
23
xx =
&
Дополним (В.20) выходным уравнением
qDxCy ][][ += . (В.21)
В соответствии с рис. В.4. выходными величинами являются
21
xy =Ω=
и
32
xy ==
ϑ
.
Поэтому имеем
⎥
⎦
⎤
⎢
⎣
⎡
=
1
0
00
10
][
C
, 0][ ≡D .
10
