Афанасьев А.А. Математические основы теории систем управления
Подождите немного. Документ загружается.


yJ
dt
yd
][= . (2.5)
Жорданова матрица
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
μ
][
0
0
][
][
][
2
1
J
J
J
J
O
состоит из
μ
диагональных клеток, имеющих следующую структуру
[]
i
J
=
,
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
i
i
i
i
i
λ
λ
λ
λ
λ
00000
10000
00100
00010
00001
L
L
LLLLLLL
L
L
L
где
−
i
λ
характеристическое число матрицы
][
A
.
Обозначим размерности клеток , , ... , . Причем + +... + =n.
Тогда систему уравнений (2.5) можно записать в развернутом виде
1
n
2
n
μ
n
1
n
2
n
μ
n
,
,
,
,
1
1
11
1
1
11
1
321
2
211
1
n
n
nn
n
y
td
yd
yy
dt
yd
yy
dt
yd
yy
dt
yd
λ
λ
λ
λ
=
+=
+=
+=
−
−
KKK
(2.6)
212
1
11
1
++
+
+=
nn
n
yy
d
t
dy
λ
,
. . . . . . . . . . . . . . . . . . .
21

n
n
y
d
t
dy
μ
λ
= .
Каждой клетке жордановой матрицы соответствует подсистема
дифференциальных уравнений. Первая подсистема (представлена в (2.6)
пунктиром) содержит уравнений, в которую входят только первые
переменных и не входят переменные из других подсистем.
1
n
1
n
Следовательно, в любую из подсистем не входят переменные из других
подсистем. Поэтому каждую подсистему можно решать независимо от других.
От этих сравнительно простых подсистем можно, оказывается, перейти к
еще более простым. Для этого сделаем замену переменных, связывая
промежуточную переменную с новой - :
i
y
i
z
,
11
1
zey
t
λ
=
22
1
zey
t
λ
=
, . . . .
1
1
1
n
t
n
zey
λ
= . (2.7)
Дифференцируем эти равенства
td
zd
eze
dt
dy
tt
1
11
1
11
λλ
λ
+= ,
. . . . . . . . . . . . . . . . .
d
t
zd
eze
d
t
dy
n
t
t
n
1
1
1
1
11
λ
λ
λ
+= .
Cравнивая правые части последних с аналогичными правыми частями
равенств из (2.6) , имеем с учетом (2.7):
d
t
zd
ezezeze
tt
t
t
1
11211
11
1
1
λλ
λ
λ
λλ
+=+ .
Сокращая экспоненциальные множители, получим дифференциальные
уравнения для новых переменных:
2
1
z
d
t
dz
=
,
3
2
z
d
t
dz
= ,
,
1
1
1
n
n
z
d
t
dz
=
−
. . . , .0
1
=
d
t
dz
n
(2.8)
Уравнения (2.8) можно компактно записать в виде, пригодном для любой
-й подсистемы :
i
zI
d
t
zd
ii
i
1
][
=
, ,...,,2,1
μ
=i (2.9)
22

где
=
1
][I
i
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
0...0000
10000
......
0...1000
0...0100
0...0010
(2.10)
- первый единичный косой ряд
i
-й подсистемы,
T
21
],...,[
i
n
iiii
zzzz =
.
Подсистема (2.8) легко решается, если начинать решение с последнего
уравнения. Интегрируя с конца, получим:
,
11
nn
Cz =
,
111
11
tCCz
nnn
+=
−−
... ,
.
)!1(
...
1
1
211
1
1
−
+++=
−
n
t
CtCCz
n
n
Возвращаясь к промежуточным переменным , имеем из (2.7):
i
y
t
n
n
e
n
t
CtCCy
1
1
1
)
)!1(
...(
1
1
211
λ
−
+++=
−
,
t
n
n
e
n
t
CtCCy
1
1
1
)
)!2(
(
1
2
322
λ
−
+++=
−
K
,
. . . . . . . . . . . . . . . . . . . . . . . . .
t
nn
eCy
1
11
λ
= .
При интегрировании первой подсистемы появилось постоянных.
1
n
Решения остальных подсистем записываются аналогично.
Совокупность решений всех
μ
подсистем образует решение системы
(2.6). Это решение зависит от
μ
nnn n +++= ...
1 2
постоянных.
Найдем фундаментальное решение системы
yJ
d
t
yd
][= . Для этого
выберем решений уравнения (2.5) при единичных начальных условиях вида: n
23

1
2
1
1
0
0
1
)0(
e
C
C
C
y
n
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
M
M
,
2
2
1
2
0
1
0
)0(
e
C
C
C
y
n
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
M
M
, . . . .
n
n
n
e
C
C
C
y =
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
1
0
0
)0(
2
1
M
M
.
В результате получаем
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
t
e
ty
0
.0
0
)(
1
1
M
λ
,
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
0
0
)(
1
1
2
M
t
t
e
te
ty
λ
λ
, . . .
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
=
−
−
0
0
0
)!2(
)!1(
)(
1
1
1
1
1
1
1
2
1
1
M
M
t
t
n
t
n
n
e
e
n
t
e
n
t
ty
λ
λ
λ
, . . .
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
=
−
−
t
t
n
t
n
n
e
e
n
t
e
n
t
ty
μ
μ
μ
μ
μ
λ
λ
μ
λ
μ
M
M
)!2(
)!1(
0
0
0
)(
2
1
. (2.12)
Эти решений образуют фундаментальную систему. Действительно,
определитель Вронского )
n
(
t
W
0
для этой системы отличен от нуля при
некотором значении , например при .tt = 0
0
=t Нетрудно видеть, что .1)0( =W
Следовательно,
−= )](...)()([)]([
21
tytytytY
n
фундаментальная система
решений.
Общее решение системы (2.5) будет иметь вид
24
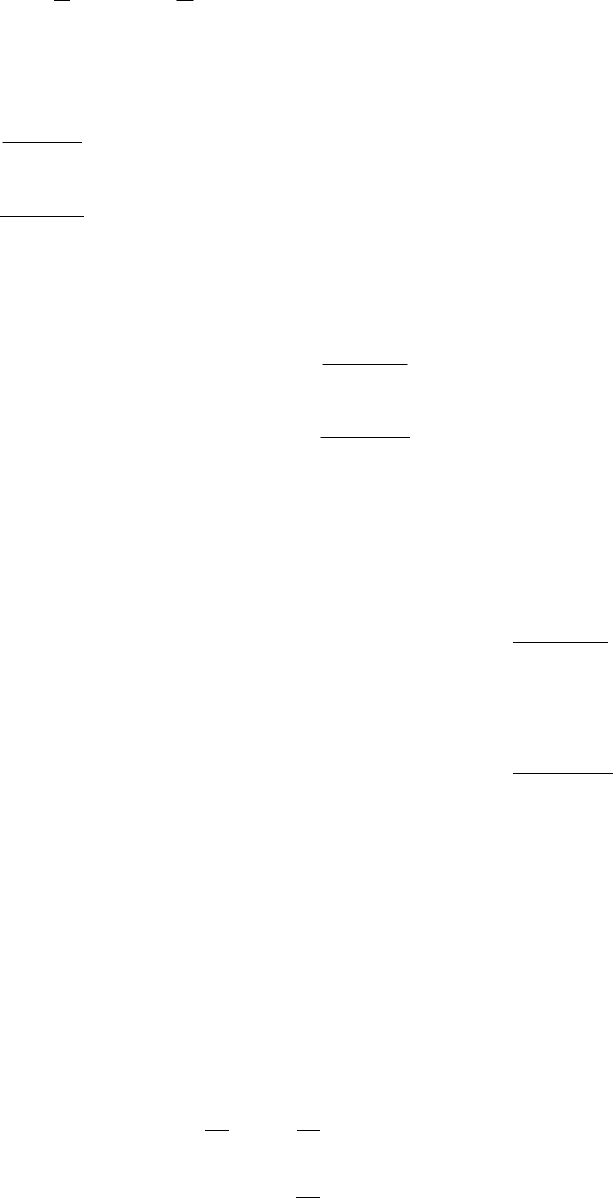
),(])([)(
0
tytYty = (2.13)
где
[]
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
−
−
−
−
=
−
−
−
−
t
e
t
e
n
n
t
t
e
n
n
t
e
e
n
t
e
e
n
t
ete
e
e
n
t
e
e
n
t
tee
tY
t
t
n
t
t
n
tt
t
t
n
t
t
n
tt
μ
λ
μ
λ
μ
μ
μ
λ
μ
μ
λ
λλ
λλλ
λ
λλ
λλλ
M
KKK
M
M
KKK
ML
LLLL
ML
ML
L
LLLL
L
L
00
)!2(
2
)!1(
1
00
0
00
)!2(
0
)!1(
0
00
00
)!2(
0
)!1(
)(
2
2
2
2
2
2
22
1
1
1
1
1
1
11
2
2
2
1
1
2
1
1
.
(2.14)
Например, для 4 первая диагональная клетка матрицы
1
=n )]([
t
Y
имеет
вид
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
t
tt
ttt
tttt
e
ete
e
t
ete
e
t
e
t
ete
1
11
111
1111
000
00
!2
0
!3!2
2
32
λ
λλ
λλλ
λλλλ
. (2.15)
25

При отсутствии кратных собственных значений матрицы
][
A
)1( =
i
n
матрица
)]([
t
Y
будет содержать только диагональные элементы вида
В этом случае имеем n подсистем (вместо
μ
с единичной
размерностью каждой.
).,...,2 n,1(ie
t
i
=
λ
)
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
t
t
t
n
e
e
e
tY
λ
λ
λ
L
LLLL
L
L
00
00
00
)]([
2
1
. (2.16)
Если известна неособенная матрица [
S
], с помощью которой матрица [
A
]
была приведена к жордановой форме, то решение исходной системы (2.1) будет
)(])([][)(][)(
0
tytYStyStx == . (2.17)
Обычно при решении уравнения (2.1) не занимаются приведением
матрицы [
A
] к жордановой форме, т.е. матрица [
S
] неизвестна.
Обратим внимание, что -я компонента общего решения (2.13),
относящаяся к
i
j
-й клетке матрицы [
t
Y (
)] при единичных начальных значениях
имеет вид:
t
j
kn
i
j
j
e
kn
tt
ty
λ
)
!)(2
1(
2
−
++++=
−
L
,
где
,,,...2,1,
1
1
j
j
q
q
nkkni =+=
∑
−
=
- количество строк в -й клетке, = 1,2, ...,
q
n
q q
μ
,
k
- номер строки в рассматриваемой -й клетке.
j
Можем -ю компоненту общего решения записать в такой форме:
i
t
jii
j
etPy
λ
)(=
, (2.18)
где
.
!
)(
0
∑
−
=
=
kn
r
r
ji
j
r
t
tP
Видим, что каждое координатное решение будет содержать только одну
экспоненту с коэффициентом затухания (собственным значением) одной из
клеток Жордана, умноженную на полином от степени не выше
t
.1−
j
n
26

Структура фундаментального решения для исходных переменных
)](][[)]([
t
Y
S
t
X
=
будет выглядеть следующим образом:
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
μμμμ
μ
μ
][][][
][][][
][][][
)]([
21
22221
11211
SSS
SSS
SSS
tX
L
LLLL
L
L
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
μ
)]([00
0)]([0
00)]([
2
1
tY
tY
tY
L
LLLL
L
L
= . (2.19)
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
μμμμμ
μμ
μμ
)]([][)]([][)]([][
)]([][)]([][)]([][
)]([][)]([][)]([][
2211
2222121
1212111
tYStYStYS
tYStYStYS
tYStYStYS
L
LLLL
L
L
Видим, что первые столбцов матрицы
1
n
)]([
t
X
tλ
2
будут иметь множителем
, следующие столбцов имеют множителем
e
и т.д.
t
e
1
λ
2
n
Следовательно,
i
-я компонента решения
)...,,2,1( nix
i
=
будет иметь
слагаемые со всеми экспонентами вида ),а не с одной, как для
решения .
...,,2,1
μ
(
λ
=je
t
j
i
y
Для выяснения характера полиномов в этих группах столбцов найдем
квадратную матрицу ,)]([][)]([
11111
tYStX =
размером , приняв для примера
n
1
.3
1
=n
Имеем
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
t
et
tt
SSS
SSS
SSS
tX
1
100
10
1
])([
2/2
333231
232221
131211
11
λ
t
e
t
S
tSStSSS
t
S
tSStSSS
t
S
tSStSSS
1
)
2
()(
)
2
()(
)
2
()(
2
31
3233313231
2
12
2223212221
2
11
1213111211
λ
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
+++
+++
+++
= .
Структура матрицы )]([
t
X в (2.19) будет следующей:
27

[]
[ ] [ ]
[] []
[] []
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
t
t
t
t
t
t
etRetR
etRetR
etRetR
tX
μ
μ
μ
λ
μμ
λ
μ
λ
μ
λ
λ
μ
λ
)()(
)()(
)()(
)(
1
1
1
1
221
111
L
LLL
L
L
,
где
[]
[
]
,)(
~
][)(
jjkjk
tYStR =
()
μ
,...,2,1, =jk - прямоугольная матрица
размером , элементы которой - полиномы от
jk
nn
×
t
степени не выше
,
)1( −
j
n
j
tY ])(
~
[
= .
t
j
j
etY
λ
/])([
Следовательно, i -я компонента общего решения (2.13) будет выглядеть
так :
),...2,1(,)()()(
11
0
nietPtytxx
t
j
ji
n
k
kkii
j
===
∑∑
==
λ
μ
, (2.20)
где полином от
t
имеет наивысшую степень не больше . 1−
j
n
Коэффициенты полиномов ) можно определить методом
неопределенных коэффициентов.
(tP
ji
ПРИМЕР 2.1.
Решить систему уравнений:
321
1
4
xxx
dt
dx
−−=
;
321
2
2
xxx
dt
dx
−+=
;
321
3
2
xxx
dt
dx
+−=
, (2.21)
[
A
]=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−−
211
121
114
.
Корни характеристического уравнения
0
211
121
114
=
−−
−−
−−−
λ
λ
λ
будут равны:
28

.3;2
321
===
λ
λ
λ
Первое решение системы ищем в виде:
T
xxxx ][
1
3
1
2
1
1
1
=
где
.,,
2
3
1
3
2
2
1
2
2
1
1
1
ttt
eaxeaxeax ===
После подстановки в (2.21) и сокращения на получим систему уравнений:
t
e
2
,42
3211
aaaa −−=
,22
3212
aaaa −+=
3
2
213
2 aaaa
+−=
.
Или
,02
321
=−− aaa
,0
31
=−
aa
0
21
=− aa
.
Ее ранг равен 2. Примем . Тогда
13
Ca =
121
Caa ==
,
112
Caa ==
.
Второе решение системы ищем в виде:
,)(
3
11
2
1
t
etbdx += ,)(
3
22
2
2
t
etbdx +=
.)(
3
33
2
3
t
etbdx +=
После подстановки в (2.21) получим, приравнивая коэффициенты при одинаковых степенях
t
:
0,0,0
321321321
=−−=−−=−− bbbbbbbbb , (2.22)
.0,0,0
321332123211
=++−=++−=++− dddbdddbdddb
(2.23)
Из (2.23) , (2.22) следует
321
bbb ==
,
.0
321
=== bbb
Тогда решение (2.23) будет
.,,
323213322
CCdddCdCd
+=+===
Общее решение системы (2.22) примет вид
29
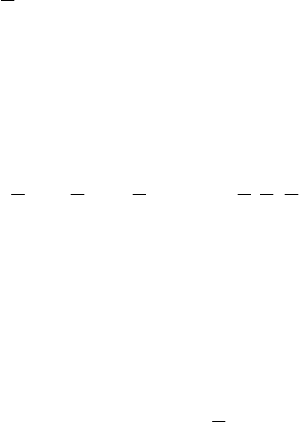
.
;
;)(
3
3
2
1
2
3
1
33
3
2
2
1
2
2
1
22
3
32
2
1
2
1
1
11
tt
tt
tt
eCeCxxx
eCeCxxx
eCCeCxxx
+=+=
+=+=
++=+=
Найдём значения постоянных, сообщающих решению фундаментальный
вид, из векторного равенства
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+
+
++
=
3
2
1
21
21
321
)0(
C
C
C
CC
CC
CCC
x .
Для фундаментального решения справедливо
.
001
010
100
][)]0()0()0([)]0([
321321
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=== eeexxxx
Отсюда из условия
1
3
2
1
e
C
C
C
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
получаем значения постоянных для первого столбца матрицы
фундаментального решения:
.1,1
321
==−= CCC
Аналогичным образом находим для второго столбца:
1,0,1
321
−=== CCC
и для третьего:
.0,1,1
321
=−== CCC
В результате фундаментальное решение получит вид
30
