Абраменко И.Г. Теория автоматического управления

Подождите немного. Документ загружается.

рр

() ()

()

() () ()

1() 1()

WsWs

Ys Y s Fs

Ws Ws

, (2.61)

где

п 124

() () () ()Ws WsWsWs=

- передаточная функция прямой цепи (эквива-

лентная передаточная функция между точкой приложения задающего воз-

действия и управляемой величиной при разомкнутом контуре обратной свя-

зи);

р 245

() () () ()Ws WsWsWs=

- передаточная функция разомкнутого контура,

получаемая при мысленном размыкании контура (чаще всего, на участке

действия сигнала обратной связи) относительно точек размыкания, вычис-

ленная без учета передаточной функции элемента сравнения.

Уравнение (2.61) представим в виде:

() () ()

Ys Y s Y s

, (2.62)

где

()

- составляющая управляемой величины, обусловленная действием

задающего воздействия;

)(sY

- составляющая управляемой величины, обу-

словленная действием возмущающего воздействия.

Обозначим:

зр

()

() 1 ()

Ys Ws

. (2.63)

Величину

()

называют передаточной функцией замкнутой сис-

темы по задающему воздействию

Аналогичным образом полученную величину

)(

)(1

)()(

)(

sWsW

(2.64)

называют

передаточной функцией замкнутой системы по возмущающему

воздействию

С учетом (2.63) и (2.64) уравнение (2.61) принимает вид:

з ,,

() () () () ()

YY YF

Ys Y sW s FsW s=+

Таким образом, исходная структурная схема может быть представлена

в следующем эквивалентном виде:

Рис. 2.17. Эквивалентная структура замкнутой САУ

Передаточные функции (2.63) и (2.64) являются основными переда-

точными функциями САУ, так как они устанавливают связь управляемой ве-

личины со входными воздействиями. Если же в процессе расчета требуется

определение передаточной функции замкнутой системы между произволь-

ными величинами, то следует применять следующее общее правило:

переда-

точная функция между любыми величинами схемы равняется дроби, у ко-

торой числитель представляет собой произведение передаточных функций

звеньев, включенных между точками приложения входной и выходной вели-

чин, а знаменатель – увеличенную на единицу передаточную функцию ра-

зомкнутого контура.

Кроме функций (2.63) и (2.64) к основным передаточным функциям

замкнутых САУ относят также функции, устанавливающие связь сигнала

рассогласования

)(sUΔ

с входными воздействиями. Применив общее прави-

ло, получим:

- для передаточной функции по сигналу рассогласования, вызванному

задающим воздействием

зр

()

() 1 ()

Ys Ws

; (2.65)

- для передаточной функции по сигналу рассогласования, вызванному

возмущающим воздействием

345

() () ()

()

() 1 ()

WsWsWs

Fs W s

==−

. (2.66)

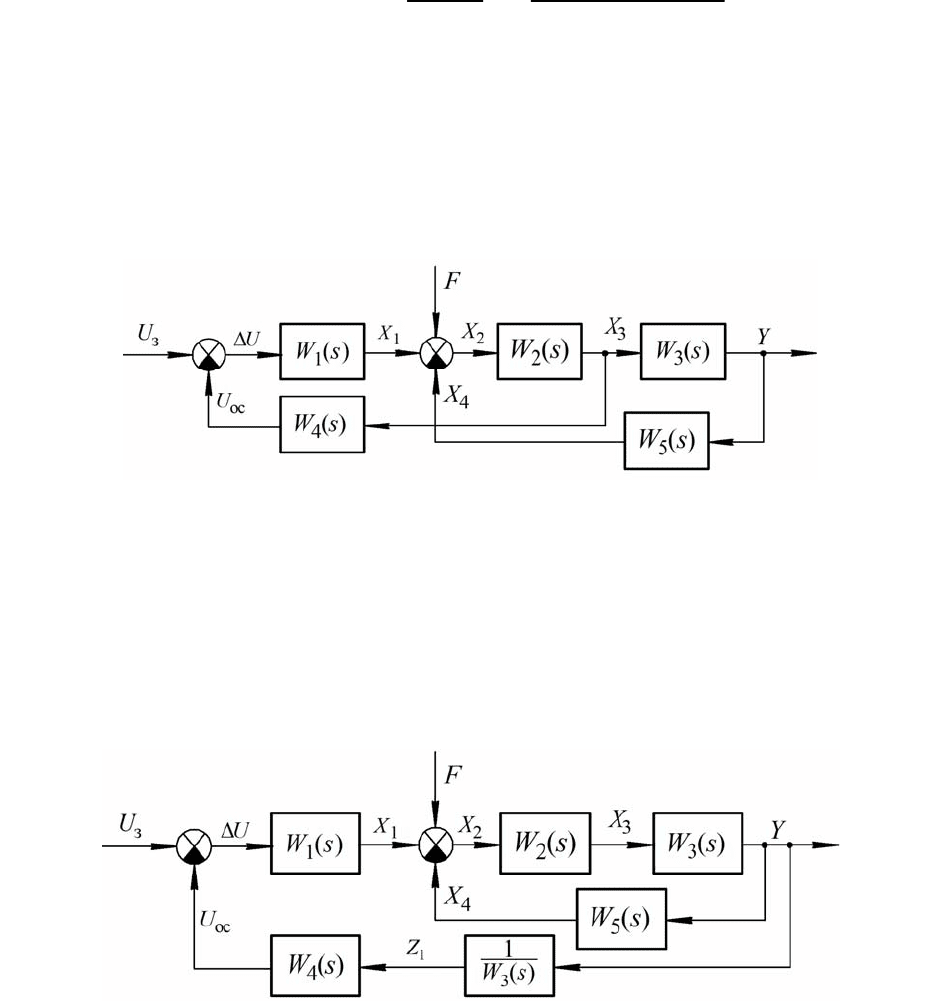
Пример 2.7.

Преобразовать к одноконтурному виду и определить основные переда-

точные функции САУ, приведенной на рис. 2.18:

Рис. 2.18. Исходная структура САУ

Решение.

Перенесем узел разветвления сигнала

через звено

)(

вперед и поме-

няем его местом с узлом разветвления сигнала

(см. рис. 2.19).

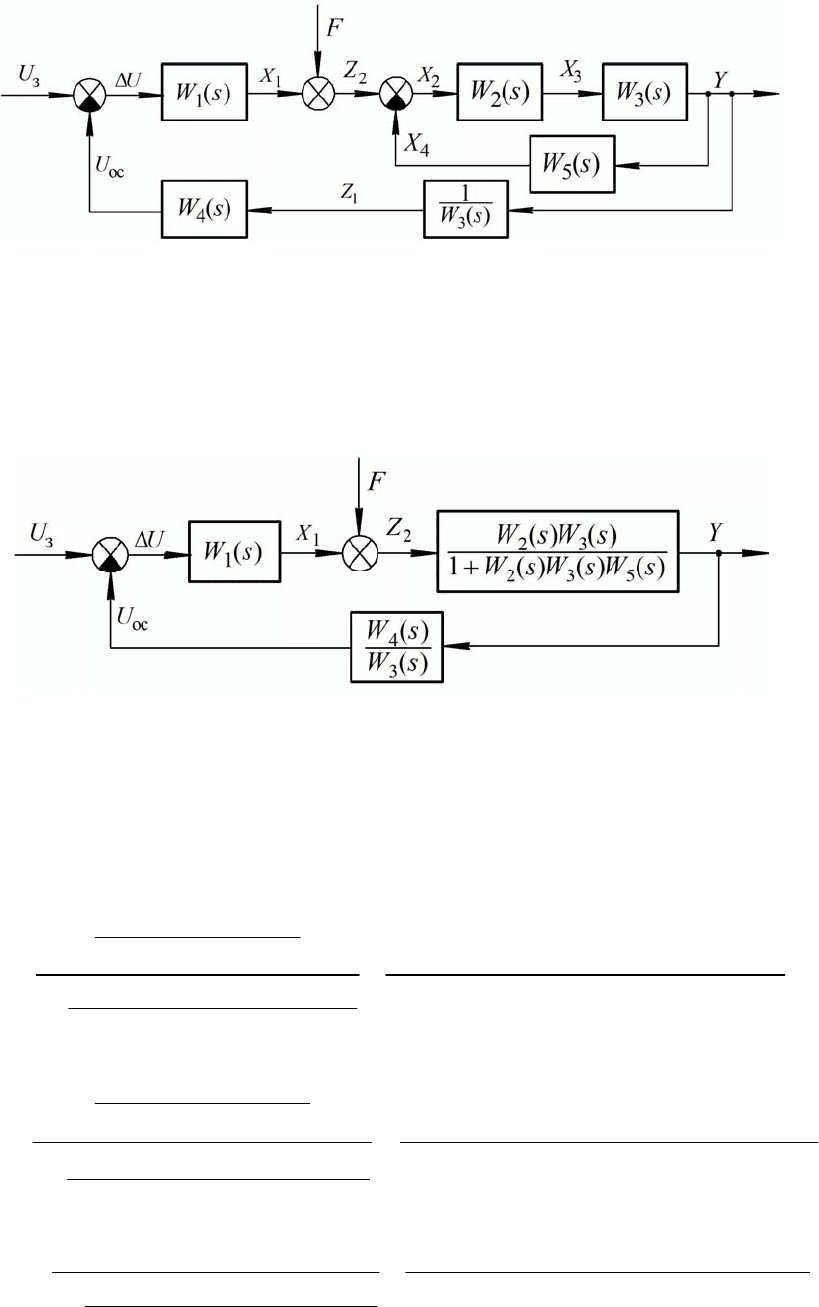
Рис. 2.19

Заменим второй блок суммирования на эквивалентное соединение двух

более простых аналогичных блока (см. рис. 2.19).

Рис. 2.20

Тогда эквивалентная одноконтурная структура САУ может быть пред-

ставлена в виде, приведенном на рис. 2.21.

Рис. 2.21

Передаточные функции системы имеют вид:

123

235 123

1234

235 124

235 3

() () ()

1()()() ()()()

()

() () () ()

1()()()()()()

[1 () () ()] ()

WsW sWs

WsWsWs WsWsWs

WsW sWsW s

WsWsWs WsWsWs

WsWsWs Ws

+⋅

;

)()()()()()(1

)()(

)()]()()(1[

)()()()(

)()()(1

)()(

)(

421532

3532

4321

532

sWsWsWsWsWsW

sWsW

sWsWsWsW

sWsWsW

sWsW

⋅+

;

235

1234

235 124

235 3

1()()()

()

() () () ()

1 ()()() ()()()

[1 () () ()] ()

WsWsWs

WsWsWsWs

WsWsWs WsWsWs

WsWsWs Ws

+⋅

;

)()()()()()(1

)()(

)()]()()(1[

)()()()(

)()]()()(1[

)()()(

)(

421532

3532

4321

3532

432

sWsWsWsWsWsW

sWsW

sWsWsWsW

sWsWsW

−=

⋅+

−

Заметим, что вариантов преобразования структурных схем существует

всегда несколько. В нашем случае, например, можно сначала перенести пер-

вый блок суммирования через звено

)(

, а затем блоки суммирования

поменять местами.

***

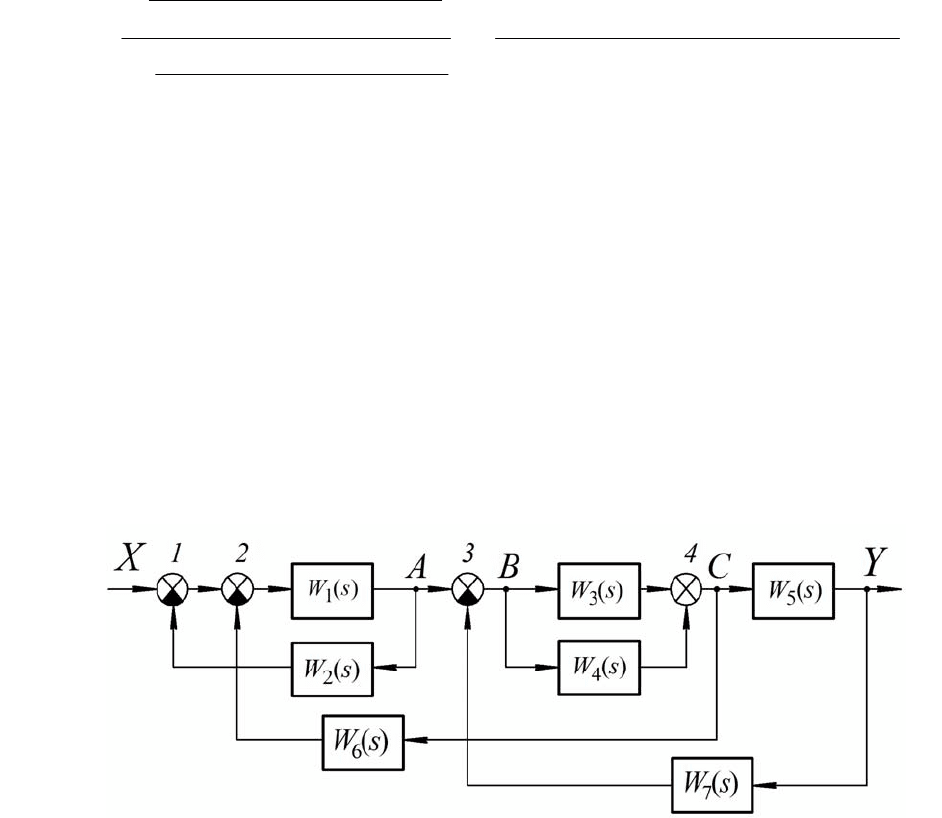
Пример 2.8.

Пусть структурная схема САУ имеет вид, приведенный на рис. 2.22.

Рис. 2.22

Найдем передаточную функцию замкнутой системы по задающему

воздействию.

Решение.

Применив правило перестановки сумматоров 1 и 2 и переноса узла

выхода на вход пятого звена

()Ws

, а затем перестановки его с узлом

, по-

лучим структурную схему без перекрестных связей.

Воспользовавшись формулами (2.54-2.56) для преобразованной схемы

можем последовательно записать:

12 34 3 4

()

() ; () () ()

1()()

Ws Ws Ws Ws

WsW s

==+

;

3457

34 5 7

()

1()()()

WsWsWs

;

12 3457

12 3457 6

() ()

1()()()

WsW s

Ws Ws

WsW sWs

Контрольные вопросы

1. Какое дифференциальное уравнение называется линейным?

2. Как составляются дифференциальные уравнения элементов САУ?

3. Объясните сущность линеаризации.

4. Что называется передаточной функцией САУ или ее элемента?

5. Как определить вид передаточной функции по заданному диф-

ференциальному уравнению?

6. Нарисуйте переходные характеристики типовых звеньев САУ.

7. Что отражает структурная схема системы управления?

8. Какие вам известны виды соединения звеньев и как определить их

передаточные фикции?

9. Назовите виды передаточных функций замкнутых САУ.

10. Какие системы называются статическими и какие астатическими?

11. Как определить передаточную функцию между произвольными пе-

ременными структурной схемы САУ?

12. Как из дифференциального уравнения элемента получить его урав-

нение статики?

13. Как получить в общем случае из дифференциального уравнения пе-

реходную функцию?

14. Как связаны друг с другом переходная и весовая функции?

15. Как из дифференциального уравнения элемента получить его пере-

даточную функцию?

16. Как от передаточной функции элемента перейти к его

уравнению

динамики в изображениях, а затем в оригиналах?

17. По каким правилам определяются эквивалентные передаточные

функции для последовательного, параллельного и встречно-параллельного

соединений линейных элементов? Запишите соответствующие формулы для

случая двух соединенных элементов.

18. Что такое разомкнутый контур системы и чему равна его переда-

точная функция?

19. Как записывается в общем случае

характеристическое уравнение

замкнутой системы через передаточную функцию разомкнутого контура?

20. Из каких составляющих складывается сигнал ошибки в типовой

системе? От каких внешних воздействий они зависят?

21. Как связаны сигнал ошибки и его составляющие с передаточной

функцией разомкнутого контура?

Главав 3. Характеристики САУ

3.1. Временные характеристики

Дифференциальные уравнения не зависимо от формы представления

является самой общей формой описания САУ и не дают наглядного пред-

ставления о всех ее свойствах. Более наглядно характеризуют эти свойства

функции

)(ty

, являющиеся решениями дифференциальных уравнений.

Известно, что одно и то же дифференциальное уравнение имеет мно-

жество решений, конкретный вид которых зависит от начальных условий и

от характера функции

)(tx

. Поэтому в ТАУ свойства систем и их элементов

характеризуют решениями, соответствующими нулевым начальным услови-

ям и одному из типовых воздействий на входе, которые называются

времен-

ными характеристиками

Наиболее широкое использование при описании динамических свойств

получила переходная функция

)(th

. Переходной функцией называют функ-

цию, описывающую изменение выходной величины, возникающее после по-

дачи на вход единичного ступенчатого воздействия

)(1 t

при нулевых на-

чальных условиях. График переходной функции называется

переходной ха-

рактеристикой.

Второй временной характеристикой является

импульсная переходная

функция

)(tw

. Под этой функцией подразумевают функцию, описывающую

изменение выходной величины, возникающее после подачи на вход дельта–

функции при нулевых начальных условиях. График

)(tw

называют импульс-

ной переходной характеристикой

Из предыдущего изложения следует, что линейные САУ описываются

дифференциальными уравнениями вида:

)()()()()()(

)1(

)(

)1(

)(

txbtxbtxbtyatyatya

+++=+++

−−

, (3.1)

где

)(tx

)(ty

– соответственно, входная и выходная величины;

– ко-

эффициенты;

– порядок уравнения.

Из курса высшей математики известно, что интегрирование уравнения

(3.1) сводится к нахождению суммы общего решения однородного уравнения

без правой части

()yt

и какого–либо частного решения неоднородного

уравнения

()yt

, т.е.:

св

() () ()yt y t y t

. (3.2)

Изменение выходной величины, определяемое составляющей

()yt

на-

зывается

свободным движением, т.к. зависит только от вида левой части

уравнения (3.1), т.е. от внутренних свойств самого объекта. Составляющая

()yt

, наоборот, зависит от характера входного воздействия и поэтому соот-

ветствующее изменение называется

вынужденным движением.

Составляющая

()yt

ищется в виде:

()

yt e=

, (3.3)

где

– некоторое рациональное число.

Подставив (3.3) в уравнение (3.1) при нулевой правой части, получим:

n pt n pt pt

ap ap aee e

−

++ =K

или

=+++

−

apapa K

. (3.4)

Последнее уравнение называется характеристическим.

Таким образом выражение (3.3) является решением исходного уравне-

ния при условии, что

является корнем уравнения (3.4). Так как это урав-

нение имеет

корней, то имеем и

линейно независимых решений

)(ty

Воспользуемся известной теоремой математики, утверждающей, что если

линейно независимых функций

)(ty

являются решениями однородного

уравнения, то общее решение этого уравнения определяется выражением:

() ()

ii i

yt Cyt Ce

∑∑

, (3.5)

где

– произвольные постоянные интегрирования.

Заметим, что выражение (3.5) справедливо только в случае, если все

корни

являются простыми. Если же какой–либо корень

имеет крат-

ность

, то в (3.5) вместо

слагаемых вида (3.3) следует включить состав-

ляющую вида:

(

)

12 1

()

jjjj jr

yt C C t C t C t e

−

++ +−

=+ + + +K

. (3.6)

Частное решение

()yt

обычно ищется в том же виде, в каком задана

правая часть

, т.е. в зависимости от вида функции

)(tx

Рассмотрим пример.

Пример 3.1.

САУ описывается дифференциальным уравнением первого порядка:

)()()( tkxtytyT

′

где:

0,5T с=

4k =

Определить временные характеристики

)(th

)(tw

Решение.

Сначала определим

)(th

Имеем характеристическое уравнение:

Его единственный корень

Tp 1

−

. Следовательно:

(

)

с 11

()

ht C Cee

−

Вынужденную составляющую

()ht

будем искать в виде

в 2

()ht C

Подставив это решение в исходное уравнение, получим

kC =

. Тогда: