Абраменко И.Г. Теория автоматического управления
Подождите немного. Документ загружается.

91
(
)
1
1
()
t
T
ht C ke
−
=
+
.
Используем начальное условие
(0) 0h
=
. Для этого запишем уравнение:
1
(0) 0hCk
=
=+
.
Откуда
kC −=
1
.
Окончательно получим:
(
)
1
2
() 1 4 1
t
t
T
ht k ee
−
−
⎡⎤
⎡
⎤
=− =−
⎢⎥
⎣
⎦
⎣⎦
.
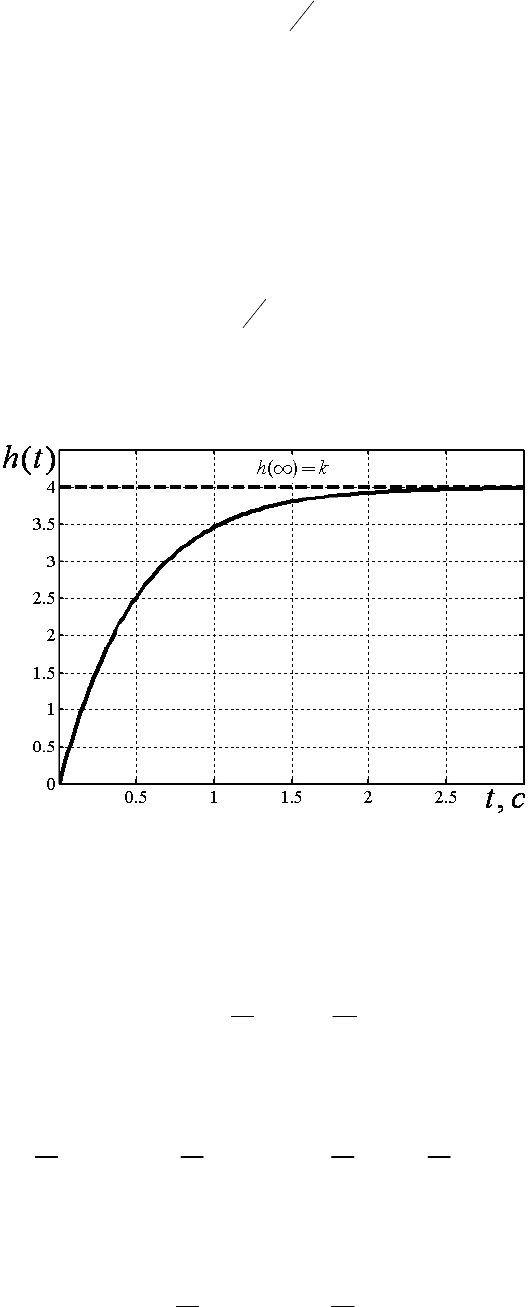
График полученного решения представлен на рис.3.1.
Рис.3.1
Для определения
)(tw
исходное уравнение преобразуем к виду:
T
w
t
T
k
w −δ=
′
)(
и проинтегрируем полученное выражение:
∫∫∫
−=−δ=
ttt
dttw
T
t
T
k
dttw
T
dtt
T
k
w
000
)(
1
)(1)(
1
)(
или
)(1)(
1
0
t
T
k
dttw
T
w
t
∫
=+
.
92
Введем обозначение
∫
=
t
zdttw
0
)(
. Тогда
zw
′
=
и
)(1
1
t
T
k
z
T
z =+
′
или
)(1 tkzzT =+
′
.
Последнее уравнение идентично исходному при условии, что
)(1)( ttx =
. Значит
(
)
1
() 1 ()
t
T
zt k hte
−
⎡⎤
=− =
⎢⎥
⎣⎦
.
Окончательно получаем:
(
)
1
22
4
() () () 8
0,5
t
tt
T
k
wt z t h t
T
eee
−
−
−
′′
=== = =
.
Таким образом:
)()( thtw
′
=
.
Последнее соотношение справедливо и для любого другого вида урав-
нения САУ, что весьма удобно при определении
)(tw
.
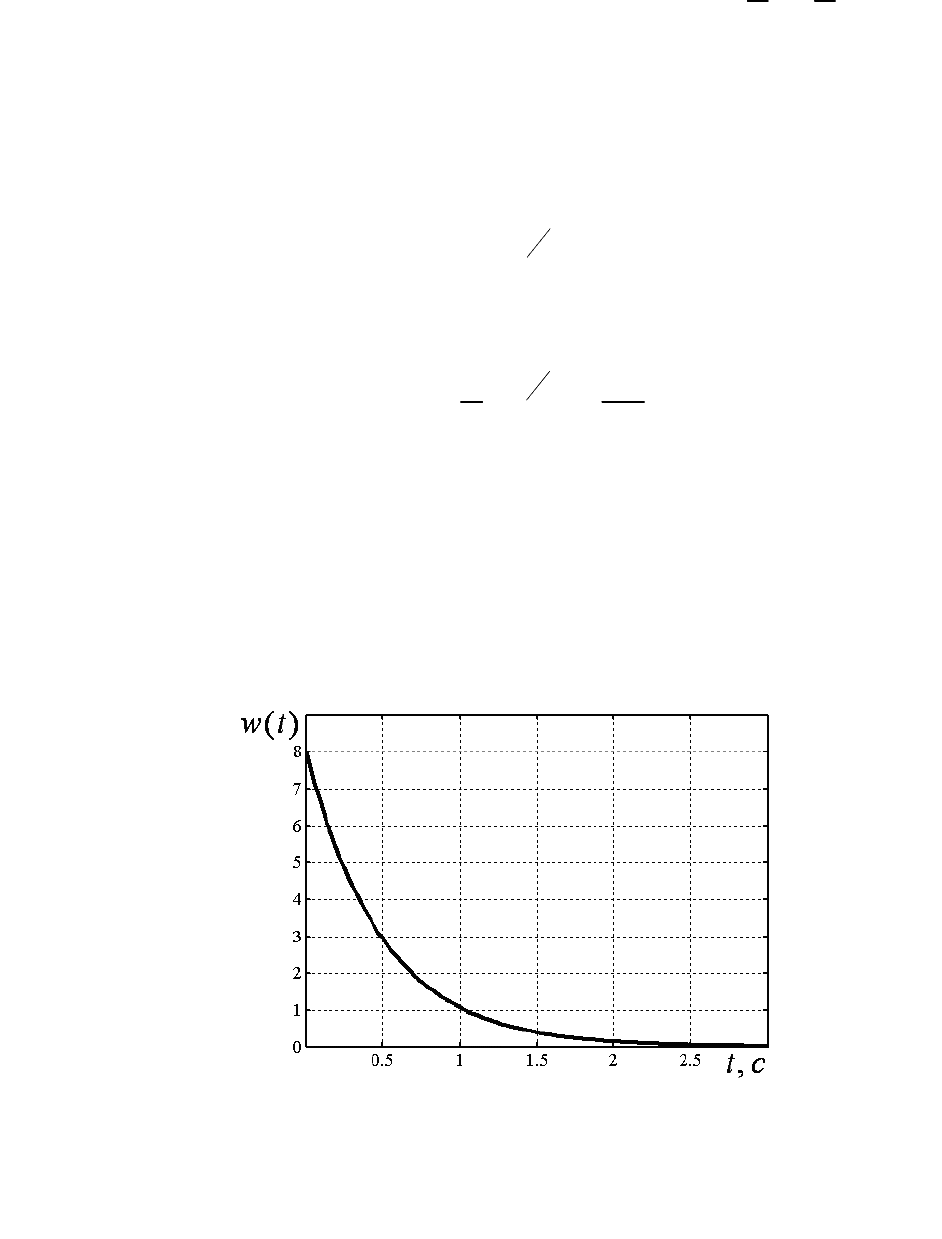
График полученного решения представлен на рис.3.2.
Рис.3.2
***
На рис.3.3,а для условий примера 3.1 представлена реакция системы
при подаче на вход линейно изменяющегося сигнала
() 2
x
tt=
, а на рис. 3.3,б
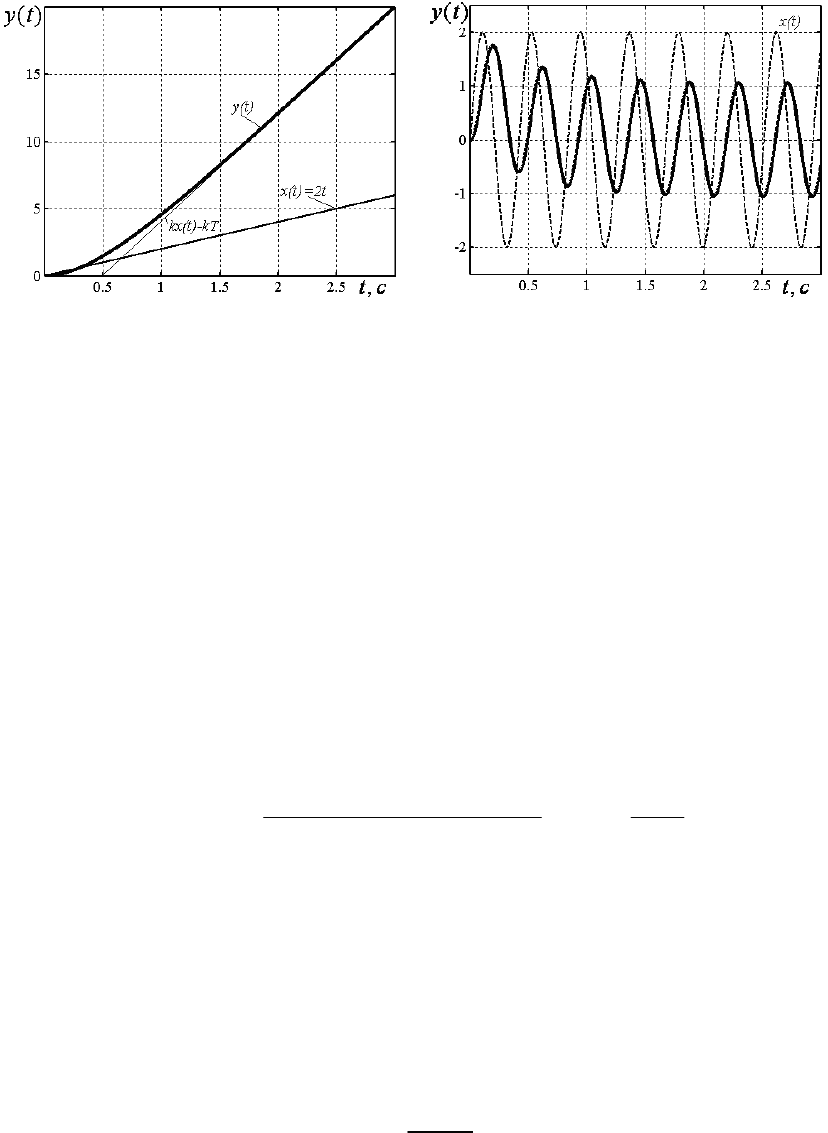
93
- гармонического сигнала
()
() sin ωxt A t
j
=+
при
2
A
=
,
1
ω 15 c
-
=
,
12,5
j
=
.
Рис.3.3
Применение преобразования Лапласа значительно упрощает определе-
ние временных характеристик.
Ход решения при этом следующий.
1.
Преобразуем исходное уравнение (3.1) по Лапласу при нулевых на-
чальных условиях:
)()()()()()(
1
10
1
10
sXbsXsbsXsbsYasYsasYsa
m
mm
n
nn
+++=+++
−−
KK
.(3.7)
2.
Решим алгебраическое уравнение (3.7) относительно )(sY при за-
данном
)(sX :
)(
)(
)(
)()(
1
10
1
10
sX
sA
sB
sX
asasa
bsbsb
sY
n
nn
m
mm
=
+++
+++
=
−
−
K
K
. (3.8)
3.
Определим оригинал решения
)(ty
.
В общем случае для нахождения
)(ty
используют обратное пре-
образование Лапласа (
1−
L
- преобразование), определяемое формулой обра-
щения Римана-Меллина:
{}
1
1
() ( ) ( )
2
j
s
t
j
f
t L Fs Fs ds
j
e
α
α
π
+∞
−
−∞
==
∫
, (3.9)
где
0
Re cs >=α
может быть любым постоянным числом
0
c>
.
94
Более простым методом является использование справочных
таблиц, в которых приводятся изображения
)(sF
и соответствующие им
оригиналы
)(ty
.
В случае, если изображение является дробно-рациональной
функцией, т.е.:
rr
rr
ll
ll
dsdsdsd
cscscsc
sD
sC
sF
++++
++++
==
−
−
−
−
1
1
10
1
1
10
)(
)(
)(
K
K
,
причем
rl <
, а коэффициенты
i
c
,
j
d
- действительные числа, применяется
формула разложения Хевисайда:
1
1
1
1
() lim ( )( )
(1)!
j
j
j
j
k
N
k
st
j
k
ss
j
j
d
ft Fs s s
k
ds
e
−
−
→
=
⎧⎫
⎪⎪
⎡
⎤
=−
⎨⎬
⎣
⎦
−
⎪⎪
⎩⎭
∑
, (3.10)
где
j
s
- корни уравнения
0)(
=
sD
;
N
- число различных корней;
j
k
-
кратность
j
-го корня.
Дифференциальные уравнения реальных САУ обычно имеют простые
корни
j
s
, и следовательно для них все
1
=
j
k
. Тогда выражение (3.10) с уче-
том соотношения
01 2 1 1
()
()( )( )( )() ()
j
j
jjjjjjr j
ss
dD s
ds s s s s s s s s s Ds
ds
−+
=
′
−− − − −= =KK
принимает более простой вид:
1
()
()
()
j
N
s
t
j
j
j
Cs
ft
Ds
e
=
⎧
⎫
⎪
⎪
=
⎨
⎬
′
⎪
⎪
⎩⎭
∑
. (3.11)
Если полином
)(sD
имеет
1
q
кратных и
2
q
простых корня, то (3.11)
записывается в виде:
1 12
1
1
1
11
()
1
() lim ( )( )
(1)! ()
j
jj
j
j
k
qqq
kst
j
st
j
k
ss
jj
jjq
Cs
d
ft Fs s s
kDs
ds
ee
−
+
−
→
==+
⎧⎫
⎧⎫
⎪⎪⎪⎪
⎡⎤
=−+
⎨⎬⎨⎬
⎣⎦
′
−
⎪⎪
⎪⎪
⎩⎭
⎩⎭
∑∑
. (3.12)

95
Поскольку определение временных характеристик САУ производится
при типовых воздействиях, приведем изображения этих воздействий
Наименование воздействия Оригинал Изображение
Ступенчатая функция
)(1 ta
a
s
Дельта-функция
)(t
δ
1
Рассмотрим примеры.
Пример 3.2.
Определить временные характеристики
)(th
и
)(tw
для САУ из приме-
ра 3.1 операторным методом.
Решение.
Определим
)(th
. Для этого преобразуем по Лапласу исходное уравне-
ние с учетом того, что
() 1()
x
tt
=
:
s
k
sHsTsH =+ )()(
.
Откуда:
2
()
(1)
kk
Hs
sTs
Ts s
==
+
+
.
Полученное выражение является дробно-рациональной функцией, к
которой можно применить формулу разложения Хевисайда. Тогда:
ksC
=
)(
;
sTssD +=
2
)(
;
12)(
+
=
′
TssD
.
Уравнение
2
() 0Ds Ts s=+=
имеет два корня:
1
0s
=
и
2
1
s
T=−
.
Воспользовавшись формулой (3.11), окончательно получим:
() ()
2
11
0
1
()
() 1
() 1 1
j
tt
st
j
t
TT
j
j
Cs
kk
ht k
Ds
eee e
--
=
мь
пп
й
щ
пп
к
ъ
==-=-
нэ
к
ъ
пп
ў
л
ы
пп
ою
е
.

96
Аналогичным образом определим
()wt
учитывая, что
() ()
x
tt
δ
=
.
Имеем:
ksWsTsW =+ )()(
;
1
)(
+
=
Ts
k
sW
;
ksC
=
)(
;
1)( += TssD
;
TsD
=
′
)(
;
1
1
s
T=−
.
Воспользовавшись формулой (3.11), окончательно получим:
()
1
1
1
()
()
()
j
t
st
j
T
j
j
Cs
k
wt
Ds T
ee
-
=
мь
пп
пп
==
нэ
пп
ў
пп
ою
е
.
***
Пример 3.3.
Уравнение САУ имеет вид:
)()()(2)(
2
txktytyTtyT ⋅=+
′
+
′′
ξ
Определим временную характеристику
)(th
при
3,0=T
с;
5,0=
ξ
;
10=k
.
Решение.
Преобразуем исходное уравнение по Лапласу при нулевых начальных
условиях:
2
10
(0,09 0,3 1) ( )ssHs
s
++ =
.
Откуда:
232
10 10
()
(0, 09 0, 3 1) 0, 09 0, 3
Hs
s
ss sss
==
+
+++
.
Используем формулу разложения Хевисайда. Имеем:
() 10Cs
=
;
32
( ) 0, 09 0,3
D
ssss=++
;
2
( ) 0, 27 0, 6 1
D
sss
′
=
++
.
Уравнение
32
( ) 0, 09 0,3 0Ds s s s=++=
имеет три корня:
1
0s
=
,
2
1, 667 2,887sj=− +
и
3
1, 667 2,887sj=− −
.
Воспользовавшись формулой (3.11), окончательно получим:
97
3
0
1
( 1,667 2,887)
2
(1,667 2,887)
2
(1,667 2,
()
10
()
() 1
10
0,27( 1,667 2,887) 0,6( 1,667 2,887) 1
10
0,27( 1,667 2,887) 0,6( 1,667 2,887) 1
10
10
1, 5 0, 866
j
st
j
t
j
j
j
t
jt
j
Cs
ht
Ds
jj
jj
j
ee
e
e
e
=
-+
--
-+
мь
пп
пп
==+
нэ
пп
ў
пп
ою
++
-+ +-+ +
+=
-- +-- +
=+
--
е
[]
{
[]
}
887) ( 1,667 2,887)
1,667 2,887 2,887
1,667
1,667
10
1,5 0,866
10 ( 5 2,887) ( 5 2,887)
10 ( 5 2,887) (cos(2,887 ) sin(2,887 )
( 5 2,887) (cos(2,887 ) sin(2,887 )
10 [10 co
tjt
tjt jt
t
t
j
jj
jtjt
jtjt
e
ee e
e
e
--
--
-
-
+=
-+
йщ
=+ -+ +-- =
къ
лы
=+ -+ + +
+- - - =
= - s(2,887 ) 5,774sin(2,887 )]tt+
g
Введем обозначения:
0
10 sinA
ϕ
=
;
0
5, 774 cosA
ϕ
=
. Решив полученные
уравнения, получим:
(
)
0
10
1, 047
5,774
arctg
ϕ
==
рад;
0
10 10
11,547
sin( ) sin(1,047)
A
ϕ
===
.
Тогда:
1,667
0
1,667 1,667
0
( ) 10 [ sin cos(2,887 ) 5,774sin(2,887 )]
10 sin(2,887 ) 10 11,547 sin(2,887 1,047).
t
tt
ht A t t
At t
e
ee
j
j
-
--
=- + =
=- + =- +
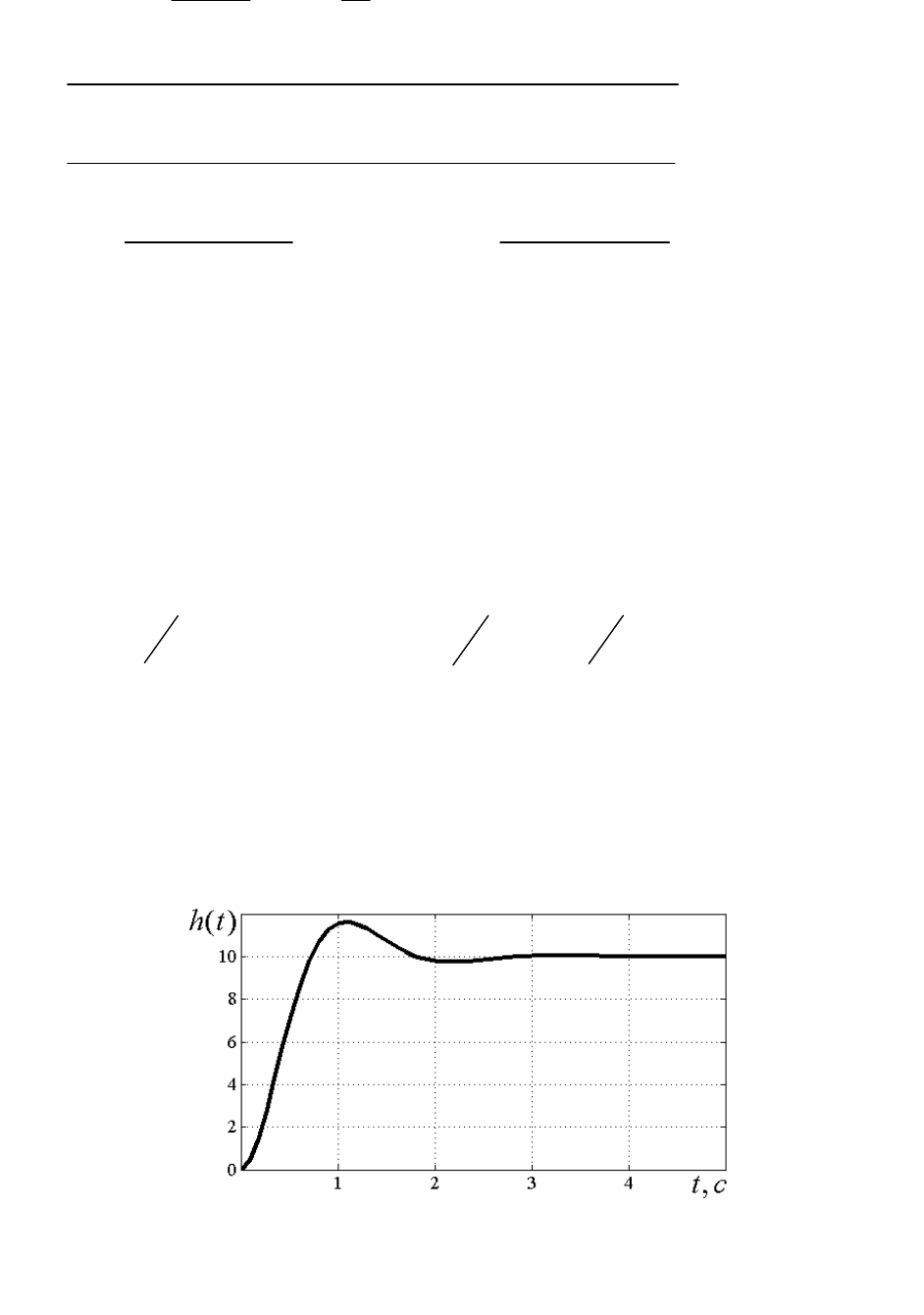
График характеристики
()ht
приведен на рисунке 3.4.
Рис. 3.4.
***

98
3.2. Частотные характеристики
Частотные характеристики описывают передаточные свойства САУ в
режиме установившихся гармонических колебаний, вызванных внешним
гармоническим воздействием. Эти характеристики широко используются в
ТАУ, так как реальные внешние воздействия могут быть представлены в ви-
де суммы гармонических сигналов. Они определяются вынужденной состав-
ляющей решения дифференциального уравнения при подаче на вход воздей-
ствия:
)sin()( tatx
ω
=
. (3.13)
Представим воздействие (3.13) с помощью формулы Эйлера в виде
суммы двух экспоненциальных воздействий:
12
() () ()
2
jt jt
xt a x t x t
j
ee
ωω
−
−
==+
, (3.14)
где
1
()
2
j
t
a
xt
j
e
ω
=
(3.15)
и
2
()
2
j
t
a
xt
j
e
ω
−
=−
. (3.16)
Решим (3.1), подставив в правую часть выражение (3.14). При этом бу-
дем искать только вынужденную составляющую решения
в
()yt
.
Используя принцип суперпозиции, решение
в
()yt
можно представить в
виде суммы двух составляющих:
в 12
() () ()yt yt yt
=
+
, где
)(
1
ty
- решение при
)()(
1
txtx =
, а
)(
2
ty
- при
)()(
2
txtx
=
.
Будем искать
)(
1
ty
в виде:
11
() ( ) () ( )
2
jt
a
yt Yj xt Yj
j
e
ω
ωω
==
. (3.17)
Подставив (3.17) и (3.15) в (3.1), после преобразований получим:

99
1
01
()
1
01
()
() () ()
2
() ()
2
jt n n
n
Aj
jt m m
m
Bj
a
Yj a j a j a
j
a
bj bj b
j
e
e
ω
ω
ω
ω
ωωω
ωω
−
−
⎡
⎤
+
++=
⎣
⎦
⎡⎤
=+++
⎣⎦
K
144444424444443
K
144444424444443
.
Из последнего выражения имеем:
()
() ()
()
Bj
Y
j
W
j
Aj
ω
ω
ω
ω
==
. (3.18)
)( ωjW
называют частотной передаточной функцией . Сравнив (3.18) с
выражением для передаточной функции
)(sW
, можно сделать вывод о том,
что
)( ωjW
является частным случаем
)(sW
при
ω
=
j
s
.
Воспользовавшись прямым преобразованием Фурье
{}
Ф () ( ) ()
j
t
f
tFj ft dte
ω
ω
∞
−
−∞
==
∫
,
можно сделать следующее определение: частотной передаточной функцией
называется отношение выходной величины ко входной, преобразованных
по Фурье при нулевых начальных условиях.
)( ωjW
, как и любая функция комплексной переменной, может быть
представлена в алгебраической и показательной формах.
Алгебраическая форма:
)()()(
ω
+
ω
=
ω
jQPjW
, (3.19)
где
)(ωP
и
)(ωQ
- вещественная и мнимая части соответственно.
Показательная форма:
()
() ()
j
Wj A e
ϕ
ω
ωω
=
, (3.20)
где
)()()(
22
ω+ω=ω QPA
- модуль, а
)(
)(
)(
ω
ω
=ωϕ
P
Q
arctg
- аргумент.
Подставив (3.20) в (3.17), получим:
[]
()
()
1
() ( ) () ()
222
jt
jt j jt
aaa
yt Wj A A
jjj
eee e
ωϕ
ω
ωϕωω
ωω ω
+
== =
.(3.21)

100
Аналогичным образом получим составляющую
)(
2
ty
:
[]
()
2
() ( )
2
jt
a
yt A
j
e
ω
ϕω
ω
−+
=
. (3.22)
Сложив (3.21) и (3.22), окончательно получим:
[][]
[]
() ()
в
() () () sin ()
2
jt jt
a
yt A A a t
j
ee
ωϕω ωϕω
ω
ωωϕω
+−+
⎡⎤
=−=⋅⋅+
⎣⎦
. (3.23)
Таким образом при гармоническом воздействии на входе выходная ве-
личина после окончания переходного процесса (
c
() 0
t
yt
→∞
=
) также изменяется
по гармоническому закону, но с другой амплитудой и фазой. При этом отно-
шение амплитуд выходной и входной величин равно модулю, а сдвиг фаз –
аргументу
)(
ω
jW
.
Кривая, которую описывает конец вектора частотной передаточной
функции на комплексной плоскости при изменении частоты от
0
до
∞
на-
зывается амплитудно-фазовой частотной характеристикой (АФЧХ).
Кроме АФЧХ, являющейся самой общей частотной характеристикой,
различают следующие разновидности частотных характеристик:
- амплитудная частотная характеристика (АЧХ) – график функции
)()( ω=ω jWA
;
- фазовая частотная характеристика (ФЧХ) – график функции
)()(
ω
=ωϕ jWArg
;
- вещественная частотная характеристика – график функции
)(Re)(
ω
=ω jWP
;
- мнимая частотная характеристика – график функции
)(Im)(
ω
=ω jWQ
.
Из сравнения (3.23) и (3.13) следует важное свойство частотных харак-
теристик – возможность их экспериментального определения на реальном
объекте.
