Абраменко И.Г. Теория автоматического управления
Подождите немного. Документ загружается.

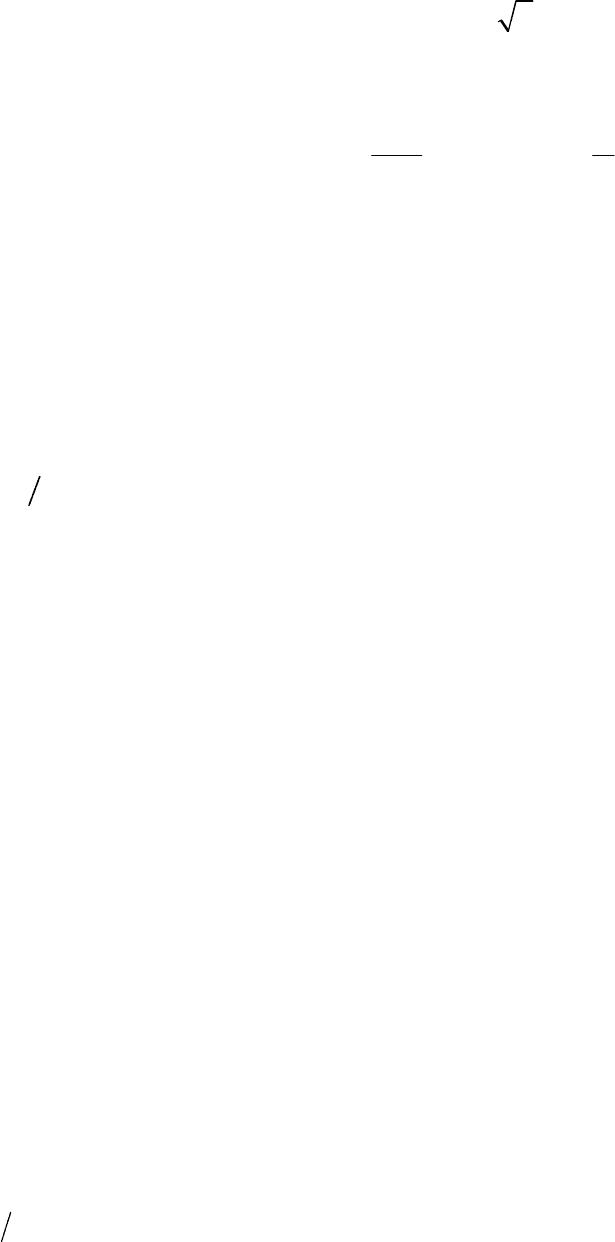
121
Максимальная ошибка аппроксимации получается при
с
ω
ω
=
и со-
ставляет:
20lg 20 lg 20lg 2 3 дбLkkΔ= − − ≈−
.
Отметим также, что при
с
ω
ω
=
:
с
1 π
( ) arctg arctg(1)
4
T
T
ϕω
⋅
=
==
.
Таким образом из анализа ЛАЧХ и ЛФЧХ видно, что с увеличением
частоты входных колебаний амплитуда выходных колебаний до частоты
с
ω
не изменяется, а при
с
ω
ω
>
- увеличивается, т.е. звено является усилителем
высоких частот.
Сдвиг фаз положителен и с ростом частоты стремится к значению
() 2
ϕ
π
∞=
.
4. Временные характеристики:
- переходная характеристика
][ )(1)()( ttTkth +=
δ
;
- импульсная переходная характеристика
() () () ()[]wt h t k T t t
δδ
′′
== +
.
4.6. Колебательное звено
1. Уравнение звена:
2
() 2ξ () () ()Tyt Tyt yt kxt
′′ ′
++=
,
где:
k
- передаточный коэффициент, представляющий собой отношение вы-
ходной величины ко входной в статическом режиме и имеющий размерность
][][][ xyk =
;
T
- постоянная времени, характеризующая инерционность зве-
122
на;
ξ
- коэффициент демпфирования (затухания), характеризующий колеба-
тельность звена.
В операторной форме при нулевых начальных условиях это уравнение
имеет вид:
)()()(ξ2)(
22
skXsYsTsYsYsT =++
.
Динамические свойства рассматриваемого звена определяются значе-
нием коэффициента
ξ
. Собственно колебательным звеном оно называется
только при
1ξ0 <<
. При
0ξ
=
звено называется консервативным, а при
1ξ ≥
- апериодическим второго порядка.
Рассмотрим случай, когда
1ξ0
<
<
.
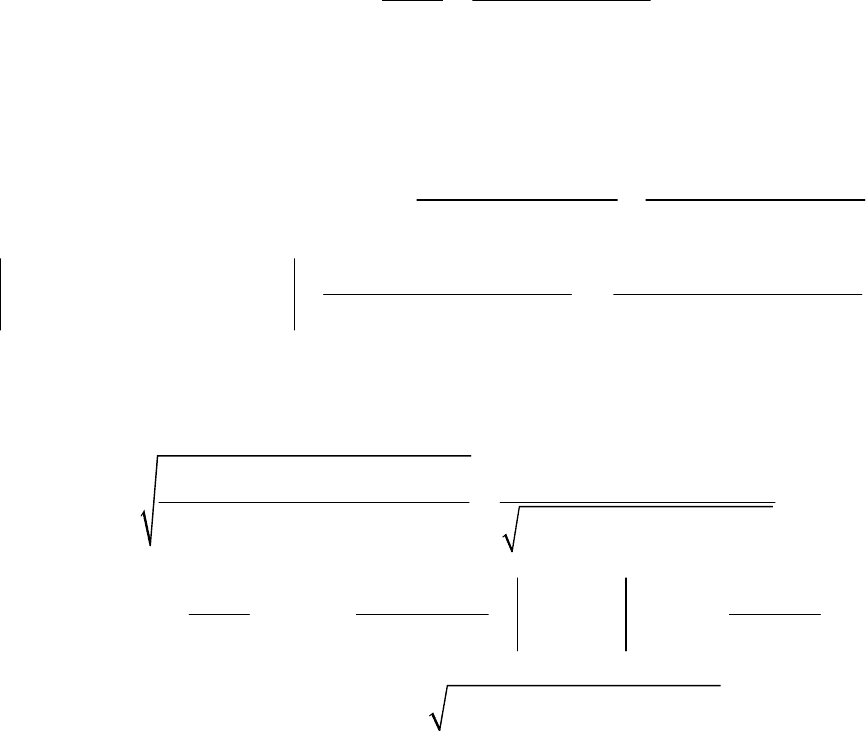
2. Передаточная функция:
22
()
()
()
2ξ 1
Ys k
Ws
Xs
Ts Ts
==
+
+
3. Частотные характеристики:
Частотная передаточная функция:
()
22 22
( ) () () ()
-211- 2
()
j
kk
Wj P jQ A
TTj TjT
e
ϕω
ωω ωω
ω
ξω ω ξω
=+ = = = =
++ +
22
222 2 222 2
умножим и разделим на
1-
2
комплексно сопр. число
1- (2 ) 1- (2 )
() ()
()
() ()
kT
kT
j
TTTT
PQ
ω
ξω
ωξω ωξω
ωω
−
==+
++
1
4444244443 14444244443
Откуда:
22222 2
222 22
222 2
1- (2 )
()
1- (2 )
1- (2 )
()
[( ) ]
()
kT kT
k
A
TT
TT
ωξω
ω
ωξω
ω
ξω
+
==
+
+
;
22 22
функция
() 2 2
( ) arctg arctg arctg
нечетная
()
1- 1-
()
QkT T
P
kT T
ω
ξω ξω
ϕω
ω
ω
ω
−
==− ==−
;
222 2
() 20lg () 20lg -20lg(1 ) (2 )LAk T T
ω
ωωξω
== −+
.
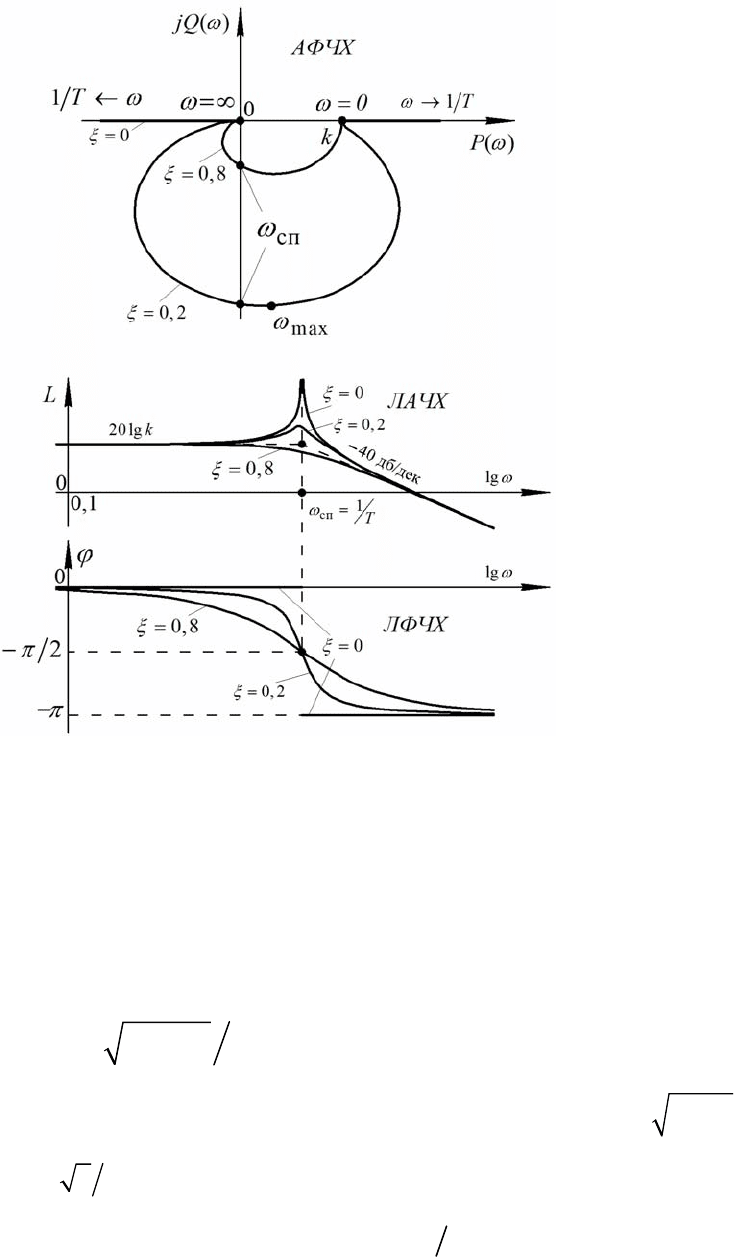
На рис.4.9 представлены соответствующие графики.
123
Рис.4.9
Вид кривой, точно соответствующей функции
()L
ω
, в существенной
степени зависит от значения коэффициента
ξ
.
Взяв производную
()L
ω
′
и приравняв ее нулю, можно получить зна-
чение частоты
2
max
12 T
ωξ
=−
, на которой наблюдается резонансный
пик ЛАЧХ, величина которого составляет
2
max
()20lg-20lg21Lk
ω
ξξ
=−
.
При этом, если
ξ 22 0,707≥≈
(
max
0
ω
≥
), ЛАЧХ имеет вид монотонно
убывающей функции. Если же
0ξ →
, то
max
1 T
ω
→
и
max
()L
ω
→∞
.
В практических расчетах обычно используют приближенную характе-
ристику, представляющую собой ломаную, состоящую из двух асимптот.
При низких частотах пренебрегают величинами
22
T
ω
и
2
(2 )T
ξ
ω
, т.е.:

124
нч
() () 20lg 20lg1 20lg
L
Lk k
ωω
≈=− =
.
Последнее уравнение представляет собой уравнение прямой, проходя-
щей через точку с координатами [
1
1 T
ω
=
;
вч 1
()20lgLk
ω
=
].
При высоких частотах пренебрегают величинами 1 и
2
(2ξ )T
ω
:
44
вч
( ) ( ) 20 lg 20 lg 20 lg 40 lg
L
LkTkT
ω
ωωω
≈=− =−
.
Определим наклон второй асимптоты:
21
10
ω
ω
=
⇒
вч 2
()20lg-40lg10Lk
ω
=
.
вч 2 вч 1
() () 40LL дб дек
ωω
−=−
.
Значение частоты
сп
ω
, при которой пересекаются обе асимптоты,
найдем из условия
нч сп вч сп
() ()LL
ω
ω
=
, т.е.:
сп
20lg 20 lg - 40lg( )kkT
ω
=
.
Отсюда
сп
1 T
ω
=
.
На основе изложенного алгоритм построения асимптотической ЛАЧХ
можно представить следующим образом:
- на уровне
() 20lg
L
k
ω
=
провести прямую до частоты
сп
ω
;
- из точки с координатами [
сп
ω
;
klg20
] провести другую прямую с
наклоном
40 дб дек−
.
ЛФЧХ строим по точкам:
0
ω
=
⇒
0)0(
=
ϕ
;
1
T
ω
=
⇒
сп
π
()
2
ϕω
=−
;
ω
=
∞
⇒
π)(
−
=
∞
ϕ
.
Таким образом, из анализа ЛАЧХ и ЛФЧХ видно, что с увеличением
частоты входных колебаний амплитуда выходных колебаний до частоты
сп
ω
не изменяется, а при
сп
ω
ω
>
- уменьшается, т.е. звено является фильтром
высоких частот.

125
Сдвиг фаз отрицателен и с ростом частоты стремится к значению
-π)( =∞
ϕ
.
4. Временные характеристики.
Переходная характеристика.
Исходя из уравнения звена, его характеристическое уравнение имеет
вид:
01ξ2
22
=++ TppT
.
Его корни
T
j
TTT
p
22
2,1
ξ-1
ξ
1ξ
ξ
±−=
−
±−=
являются комплексно-сопряженными.
Обозначим
βα
2,1
jp ±−=
и определим свободную составляющую
c
()ht
:
c1 2 1 2
12
()()
()
[]
j
tjtjt jt
tt
ht C C C C
jt jt
t
CC
eeeeee
ee e
α
βαβ β β
αα
ββ
α
−
+−− −
−−
=+ =+ =
−
−
=+
.
Представим
c
()ht
в тригонометрической форме. Для этого воспользу-
емся формулами Эйлера:
cos sin ;
cos sin .
ja
a
j
a
ja
a
j
a
e
e
⎧
⎪
=+
⎨
−
=−
⎪
⎩
Тогда:
c1 2
12 12
α
() (cosβ sin β )(cosβ sin β )
α
()cosβ ()sinβ )
[]
[]
t
ht C tjtC tjt
t
CC tjCC t
e
e
−
=++−=
−
=++−
.
Так как
с
()ht
является решением уравнения при любых значениях
1
C
и
2
C
, то:
*
12 с
**
12c
α
1
() cosβ ;
2
α
;()sinβ .
22
при
при
t
CC ht t
jj
t
CCht t
e
e
−
⎧
==⇒ =
⎪
⎨
−
=− = ⇒ =
⎪
⎩
126
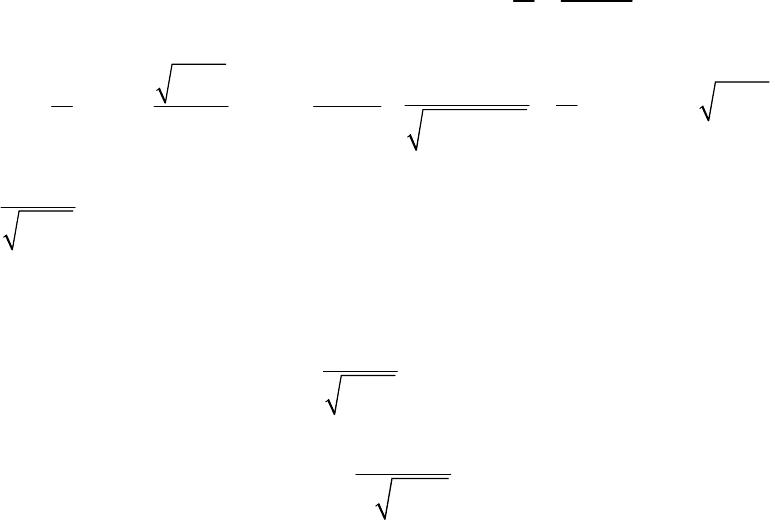
Поскольку
*
c
()ht
и
**
c
()ht
линейно независимы, то можем записать:
***
c3c 4c 3 4
α
() () () ( cosβ sin β )
t
ht Ch t Ch t C t C t
e
−
=+ = +
.
Введем обозначения:
03
sin
ϕ
AC
=
;
04
cos
ϕ
AC
=
.
Тогда:
00 0
sin cos cos sin sin( )AtAtAt
ϕ
βϕβ βϕ
+
=+
,
и, следовательно,
c0
α
() sin(β )
t
ht A t
e
ϕ
−
=+
.
Вынужденную составляющую решения будем искать в виде
в 5
()ht С
=
.
Подставив это решение в исходное уравнение при
)(1)( ttx =
, получим
kС =
5
.
Далее можем записать:
св 0
() () () sin( )
t
ht h t h t A t ke
α
βϕ
−
=+= ++
.
Импульсная переходная характеристика:
00
() () cos( ) sin( )[]
t
thtA t t
e
α
ω
ββϕαβϕ
−
′
== +− +
.
Далее, воспользовавшись нулевыми начальными условиями, опреде-
лим значения постоянных интегрирования
A
и
0
ϕ
:
0
00
0sin
0cossin)
(
Ak
A
βα
ϕ
ϕ
ϕ
=+
⎧
⎨
=−
⎩
;
⇒
0
0
0
sin
cos
t
g
β
α
ϕ
ϕ
ϕ
==
;
2
0
1-
arctg arctg
ξ
β
αξ
ϕ
==
;
0
sin
k
A
ϕ
=−
;
0
2
0
sin
1-sin
β
α
ϕ
ϕ
=
;
2
0
sin 1-
ξ
ϕ
=
;
2
1-
k
A
ξ
=−
.
Окончательно получим:
0
2
1
() 1 sin( )
1-
t
ht k t
e
α
βϕ
ξ
⎡
⎤
−
⎢
⎥
=− +
⎢
⎥
⎣
⎦
;
2
() () sin
1-
k
t
wt h t t
T
e
α
β
ξ
−
′
== ⋅
.
127
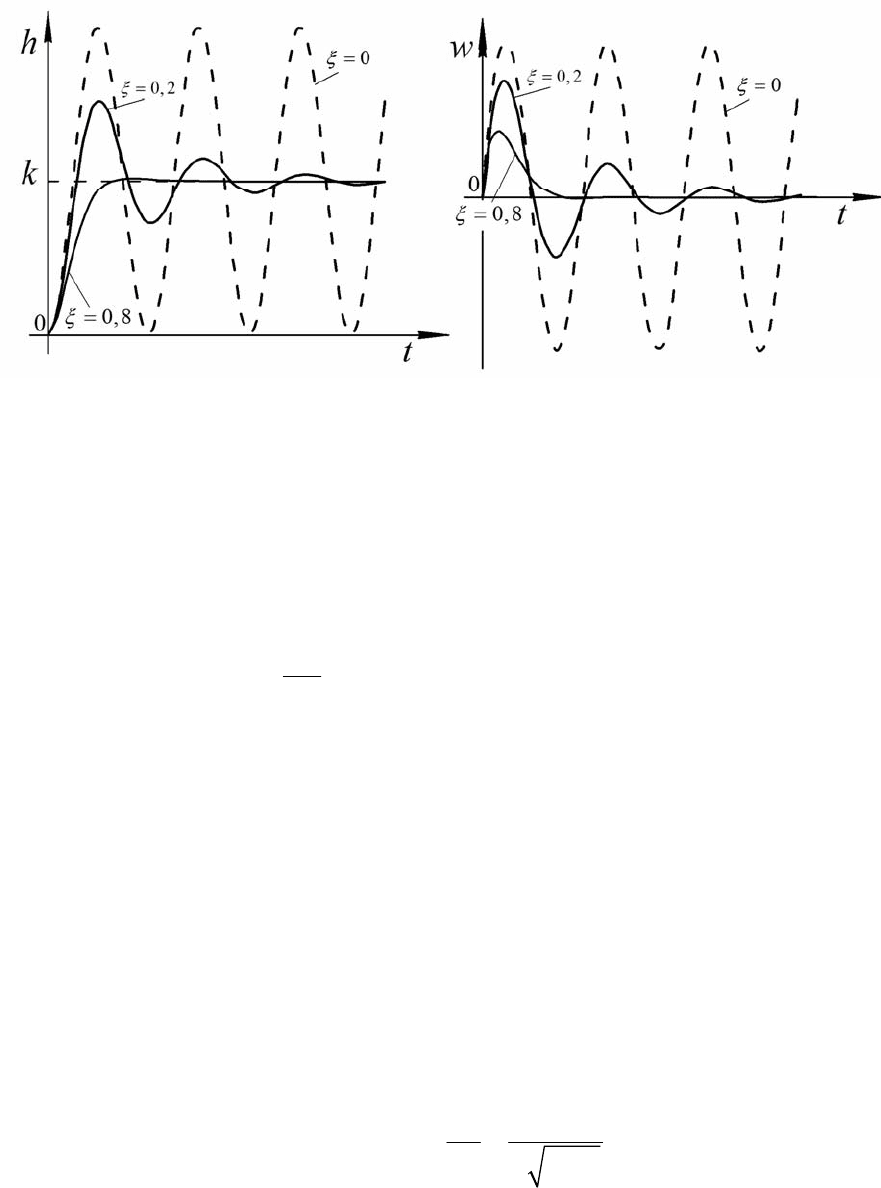
Вид этих характеристик представлен на рис. 4.10.
Рис.4.10
Характеристика
h(t)
представляет собой синусоиду, амплитуда кото-
рой убывает по экспоненциальным огибающим:
к
к
α
(0 ) 1 -
α
1
2
сверху и
снизу
()
()
()
K
t
hTnk
T
t
hTnk
e
e
−
−
⎧
+=−
⎪
⎨
−
+=−
⎪
⎩
,
где
к
T
- период колебаний;
n
- номер точки, общей и для соответствующей
экспоненты и для переходной характеристики.
Определим период колебаний
к
T
. Для этого составим систему уравне-
ний:
10
к 20 к
0t
tT T
γϕ
γ
ϕβ
+
=⇒ =
⎧
⎨
=⇒ =
⎩
,
Откуда
21 0 к 0 к
2 TT
γ
γπϕβϕβ
+−= = − =
и, следовательно:
к
2
22
1-
T
T
T
π
π
β
ξ
==
.
Следовательно, с ростом
ξ
увеличивается и период
к
T
.
Определим зависимость максимального значения переходной характе-
ристики от
ξ
:
128
() () 0tht
ω
′
==
⇒
2
2
1-
sin 0
1-
T
m
t
k
t
T
T
e
ξ
ξ
ξ
−
⋅
=
⇒
2
1-
sin 0
m
t
T
ξ
=
⇒
2
1-
m
t
T
ξ
π
=
⇒
2
1-
m
T
t
π
ξ
=
.
Тогда:
2
0
sin
2
22
1- 1-
0
22
1-
1-
1
1sin 1
1- 1-
()
T
T
m
T
hk k
T
ee
ϕ
ξπ ξπ
ξξ
ξ
ξπ
ϕ
ξξ
−=−
−−
⎡⎤
⎢⎥
⎡⎤
⎢⎥
⎢⎥
⋅
=− + =+
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎣⎦
⎢⎥
⎣⎦
144424443
Из последнего соотношения следует, что с ростом
ξ
значение
m
h
уменьшается (т.к.
2
ξ-1
уменьшается быстрее, чем растет
ξπ
).
Скорость затухания колебательных процессов принято оценивать сте-
пенью затухания:
1
21
A
AA
−
=Ψ
,
представляющей собой отношение разности двух соседних амплитуд к пер-
вой из них.
Очевидно, что чем ближе
Ψ
к единице, тем быстрее затухают колеба-
ния, и, наоборот, чем ближе
Ψ
к нулю, тем затухание медленнее. Покажем,
что
Ψ
зависит от соотношения действительной и мнимой частей корней
характеристического уравнения.
Для этого, воспользовавшись уравнением верхней экспоненциальной
огибающей, запишем:
1
1,
1[]
t
m
hke
α
−
=+
;
()
1 к
2,
1[]
tT
m
hke
α
+−
=+
.
Тогда
129
()
11к
1, 2, 1, 2,
1
1, 1,
()-( )
1-1
1
()( )
()
ttT
t
mmmm
mm
hkh khh
kk
hk hk
kk
ee
e
α
α
α
+−−
−
−−−
++
Ψ= = = =
−−
+−
11
1
1
2
-
11
ttT
t
t
K
eee
ee
e
β
α
π
α
αα
α
α
−−−
−
−
−
==−=−
.
Отношение
μ
βα
=
называют степенью колебательности.
Таким образом
2
1 e
π
μ
−
Ψ= −
.
Из последнего выражения видно, что чем меньше действительная часть
α
, тем затухание медленнее (
0α
=
⇒
μ
βα
=
=∞
⇒
0Ψ=
), и наобо-
рот, чем меньше мнимая часть
β
, тем затухание быстрее (
0
β
=
⇒
0
μ
=
⇒
1=Ψ
).
Степень колебательности связана с коэффициентом демпфирования
ξ
соотношением:
22
1- 1-
T
T
ξ
ξ
β
μ
α
ξξ
== ⋅=
.
Взаимосвязь коэффициентов
μ
,
Ψ
и
ξ
представим в виде следую-
щей таблицы:
Степень колеба-
тельности
μ
Степень
зат
у
хания
Ψ
Коэффициент
д
емпфирования
ξ
∞
0 0
0 1 1
Анализ приведенных данных показывает, что смысл коэффициента
μ
является противоположным смыслу коэффициентов
Ψ
и
ξ
.
Как отмечалось выше, при
0
ξ
=
звено второго порядка называется
консервативным. В этом случае:
1
)(
22
+
=
s
T
k
sW
;
22
() ()
1-
k
Wj P
T
ω
ω
ω
==
;
() 0Q
ω
=
;
1,2
p
j
β
=±
;
1
T
β
=
;

130
00
1
( ) 1 sin arctg arctg 1 sin (1 cos )
02 2
() ()htkt ktkt
ππ
β
ϕϕ β β
⎡⎤
⎡⎤
=− + == = ∞==− + =−
⎢⎥
⎣⎦
⎣⎦
;
() () sin
k
wt h t t
T
β
′
==
.
Следовательно временные характеристики консервативного звена
имеют вид незатухающих колебаний частотой
β
.
При
1
ξ
≥
колебательное звено вырождается в апериодическое звено
второго порядка. При этом:
sTsT
k
TssT
k
sW
21
22
1
1
1
1ξ2
)(
+
⋅
+
=
++
=
,
где
2
21
TTT =
и
TTT ξ2
21
=+
.
Таким образом в этом случае имеем два последовательно соединенных
апериодических звена первого порядка. Можно показать, что корни характе-
ристического уравнения
2
1,2
-1
p
T
ξξ
±
−
=
здесь являются вещественными
отрицательными и
12
--
12
12 12
() 1-
--
tT tT
TT
ht k
TT TT
ee+
⎡⎤
=
⎢⎥
⎣⎦
.
Если же
1
ξ
=
то
TTT
=
=
21
и
-t T
() 1 1()
t
ht k
T
e
⎡
⎤
=−+
⎢
⎥
⎣
⎦
.
4.7. Запаздывающее звено
1. Уравнение звена:
() ( )yt xt
τ
=
−
,
где
τ
- время запаздывания, является трансцендентным.
В операторной форме при нулевых начальных условиях это уравнение
имеет вид:
() ()
s
Ys Xse
τ
−
=
.
