Абраменко И.Г. Теория автоматического управления
Подождите немного. Документ загружается.

171
ошибке, вызванной входным воздействием
)(tu
в окрестностях точки
0
=
s
,
что в области оригиналов соответствует
∞
=
t
, рядом Маклорена (частного
случая ряда Тейлора при
0
0
=
s
), т.е.:
23
,, ,
23
,,
23
0
0
00
() () ()
11
() ()
2! 3!
uu u
uu
s
s
s
s
dW s d W s d W s
WsWs s s s
ds
ds ds
δδ δ
δδ
=
=
==
≈+ + +
Обозначим:
,0,
0
()
uu
s
Ws C
δ
=
=
;
,
1,
0
()
u
u
s
dW s
C
ds
δ
=
=
;
2
,
2,
2
0
()
1
2!
u
u
s
dW s
C
ds
δ
=
=
;
3
,
3,
3
0
()
1
3!
u
u
s
dW s
C
ds
δ
=
=
.
Тогда изображение составляющей ошибки
()
u
s
Δ
можно представить в
виде:
,0,1,2,3,
,
11
() () () () ...
2! 3!
uuuuuu
sUsW sUsC Cs C C
δ
⎛⎞
Δ= ⋅ = + + + +
⎜⎟
⎝⎠
или, перейдя к оригиналам, в виде:
23
0, 1, 2, 3,
23
() 1 () 1 ()
() () ...
2! 3!
uuu u u
du t d u t d u t
Cut C C C
dt
dt dt
δ
∞= + + + +
(6.7)
Подчеркнем, что последнее соотношение справедливо только при
∞→
t
.
Коэффициент
u
C
,0
называют коэффициентом статической ошибки;
u
C
,1
- коэффициентом скоростной ошибки;
u
C
,2
- коэффициентом ошибки
от ускорения;
u
C
,3
- коэффициентом ошибки по первой производной от ус-
корения и т.д.
Конкретные значения коэффициентов ошибок определяются видом
соответствующих передаточных функций.
Пример 6.3.
172
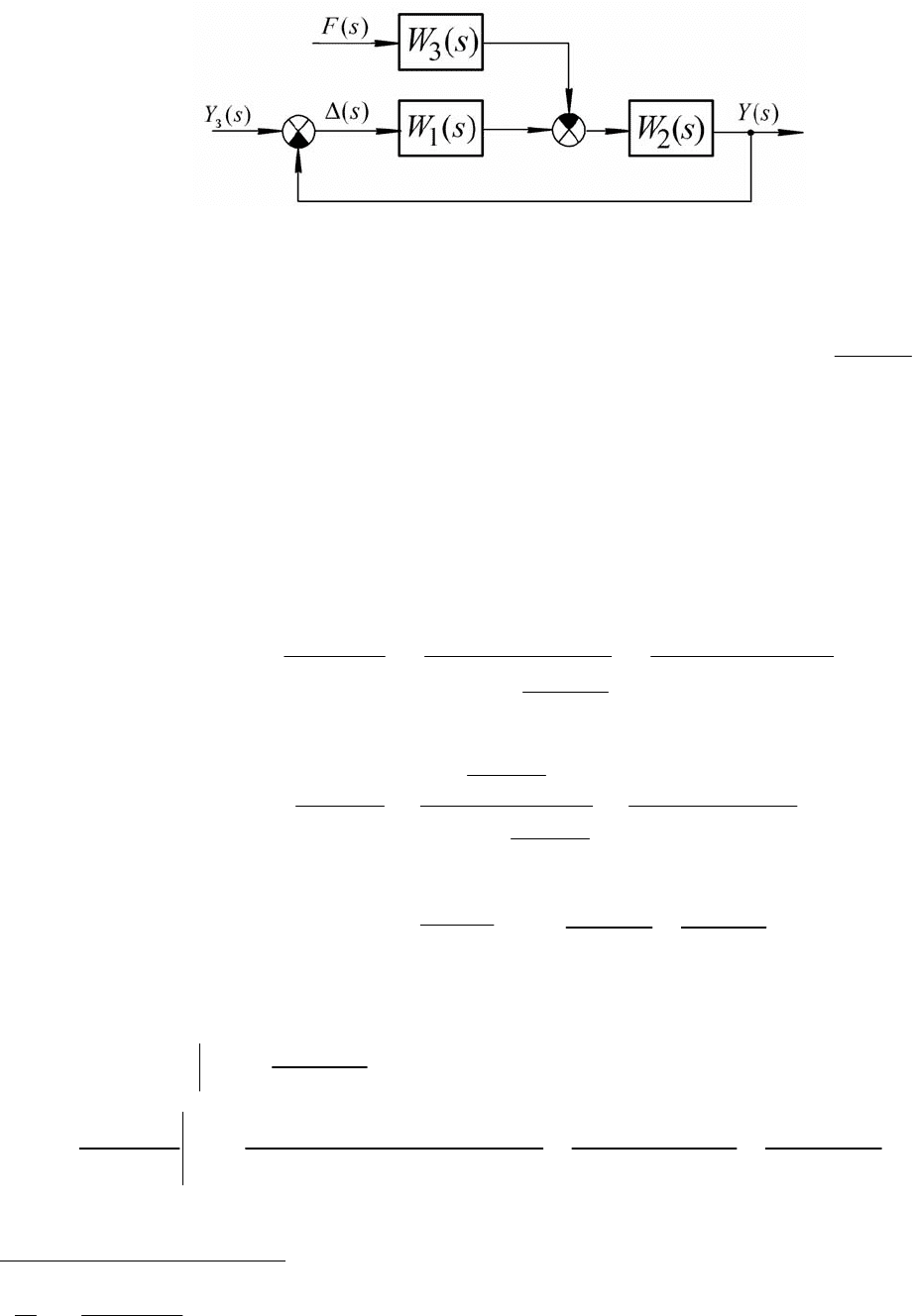
Определить ошибку системы программного управления, структурная
схема которой приведена на рис. 6.6:
Рис. 6.6
Здесь:
з
()yt at=
;
0
() constft f
=
=
;
11
)( ksW
=
;
1
)(
2
2
+
=
Ts
k
sW
;
3
()
f
Ws k=
.
Решение.
В соответствии со схемой имеем:
з
з
,
2
з 12
1
()
11
() ;
() 1
1
1
y
y
s
Ts
Ws
k
Ys Ts kk
k
Ts
δ
Δ
+
== =
++
+⋅
+
2
2
,
2
12
1
()
1
()
() 1
1
1
f
ff
f
kk
skk
Ts
Ws
k
F
sTskk
k
Ts
δ
Δ
+
== =
++
+⋅
+
Учитывая вид
з
()
y
t
, имеем:
з
()dy t
a
dt
=
;
23
зз
23
() ()
... 0
dyt dyt
dt dt
=
==
.
Тогда коэффициенты ошибок будут равны
∗
:
зз
0, ,
0
12
1
() ;
1
yy
s
CWs
kk
δ
=
==
+
()
(
)
()
(
)
()
()
з
,
12 12
12
1,
222
0
12 12 12
()
111
;
111
u
y
s
dW s
TTs kkTTs T kkT
Tk k
C
ds
Ts kk kk kk
δ
=
++ − + + −
== = =
++ + +
2
V
UVVU
V
U
′
−
′
=
′
⎟
⎠
⎞
⎜
⎝
⎛

173
2
0, ,
0
12
()
1
F
ff
s
kk
CWs
kk
δ
=
==
+
Воспользовавшись (6.7), окончательно получим:
()
зз
2
12
0, з 1, 0, 0
2
12 12
12
()
1
( ) () ()
11
1
f
з
yy f
kk
dy t
Tk k
CytC Cft at a f
dt k k k k
kk
δ
∞= + + = + + =∞
++
+
Следовательно, система не пригодна для программного управления.
***
Пример 6.3.
Определить ошибку системы программного управления для условий
примера (6.3), но при
s
k
sW
1
1
)( =
.
Решение.
Имеем:
(
)
()
з
з
2
,
2
12
з 12
12
()
1
1
() ;
() 1
1
1
y
y
s
sTs
Ts s
Ws
kk
Ys sTs kk
Ts s k k
s
Ts
δ
Δ
+
+
== = =
++
++
+⋅
+
()
2
22
,
2
12
12
12
()
1
()
() 1
1
1
f
fff
f
kk
skkskks
Ts
Ws
kk
Fs sTs kk
Ts s k k
s
Ts
δ
Δ
+
== = =
++
++
+⋅
+
Коэффициенты ошибок:
з
0, ,
0
() 0;
з
yy
s
CWs
δ
=
==
(
)
(
)
(
)
()
()
з
22
12
,
1,
2
2
12
0
12
21 21
()
1
;
u
y
s
Ts s k k Ts Ts s Ts
dW s
C
ds k k
Ts s k k
δ
=
++ + − + +
== =
++
0, ,
0
() 0
ff
s
CWs
δ
=
==
Тогда:
з
з
1,
12
()
1
()
y
dy t
Ca
dt k k
δ
∞= =
174
Система астатическая и по
з
()yt
и по
)(tf
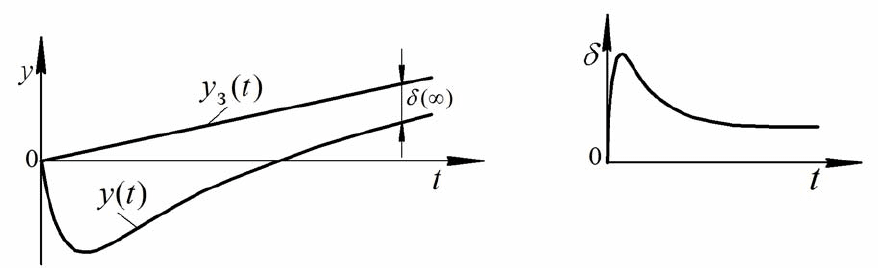
, но имеет постоянную уста-
новившуюся ошибку по скорости изменения задания (см. рис. 6.7):
а) б)
Рис. 6.7:
а) характер изменения
з
()
y
t
и
()yt
;
б) характер изменения ошибки
()
δ
∞
6.2. Точность работы САУ в переходных режимах.
Точность работы в переходных режимах определяется совокупностью
отдельных мгновенных значений ошибки
)(t
δ
. С целью стандартизации по-
казателей качества в этом случае принято использовать переходные характе-
ристики по каналу задания
)(th
y
и каналу возмущения
)(th
f
при подаче на
соответствующие входы типовых сигналов вида
)(1 t
, которые в обобщенном
виде характеризуют значения
)(t
δ
.
Показатели качества, в зависимости от способа их определения, разде-
ляются на прямые и косвенные. В начале рассмотрим прямые показатели,
которые определяются непосредственно по временным характеристикам.
При этом может использоваться как переходная характеристика
)(th
(обычно
по каналу задающего воздействия), так и импульсная переходная характери-
стика
)(t
ω
(по каналу возмущения).
175
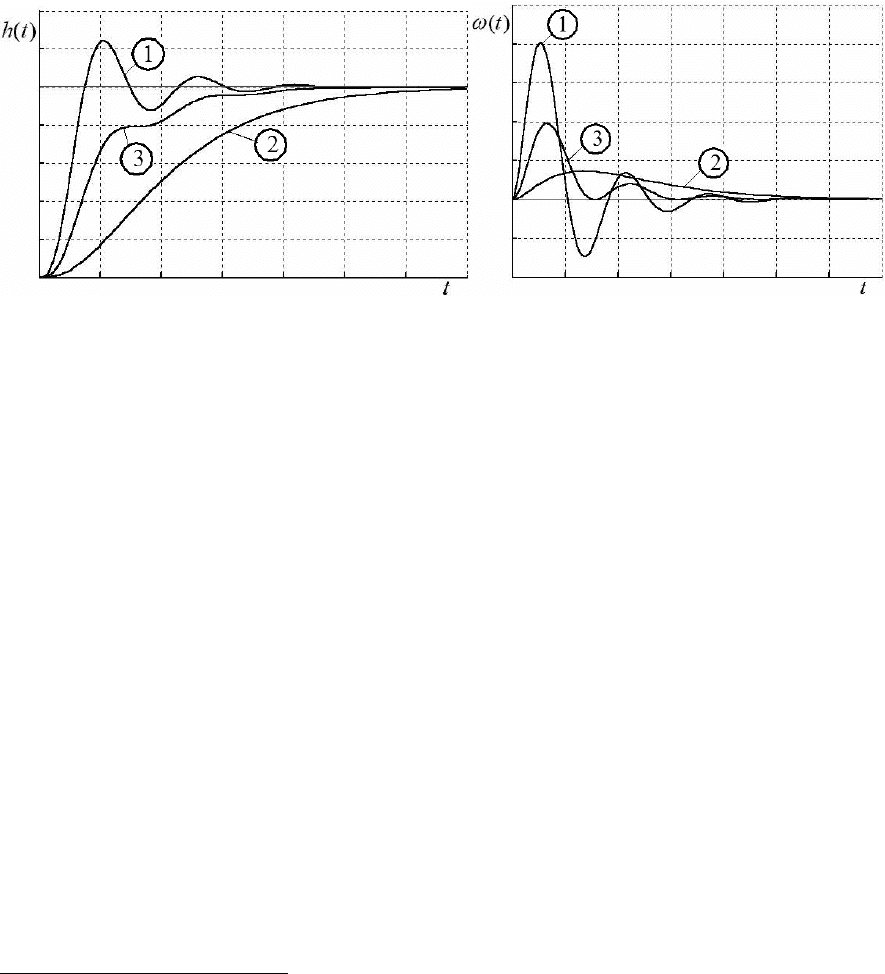
При самой общей оценке качества, прежде всего, обращают внимание
на форму переходного процесса. Различают следующие типы переходных
процессов (см. рис. 6.8):
1
- колебательные (1);
- апериодические (2);
- монотонные (3).
а) б)
Рис. 6.8:
а) переходные характеристики;
б) импульсные переходные характеристики
Наибольшее количество прямых показателей введено для характери-
стики качества колебательного процесса по каналу задания. Поэтому опреде-
ление этих показателей проведем именно для такого процесса (см. рис. 6.9):
1
Стр: 175
Рисунки соответствуют системе третьего порядка с корнями:
1 -
5,3
1
−=p , 41
3,2
jp ±
−
= - (d_ur3p_bezu_k);
2 -
5,3
1
−=p ,
01
3,2
jp ±−
=
- (d_ur3p_bezu_a);
3 -
1
1
−=p , 41
3,2
jp ±−= - (d_ur3p_bezu_m)
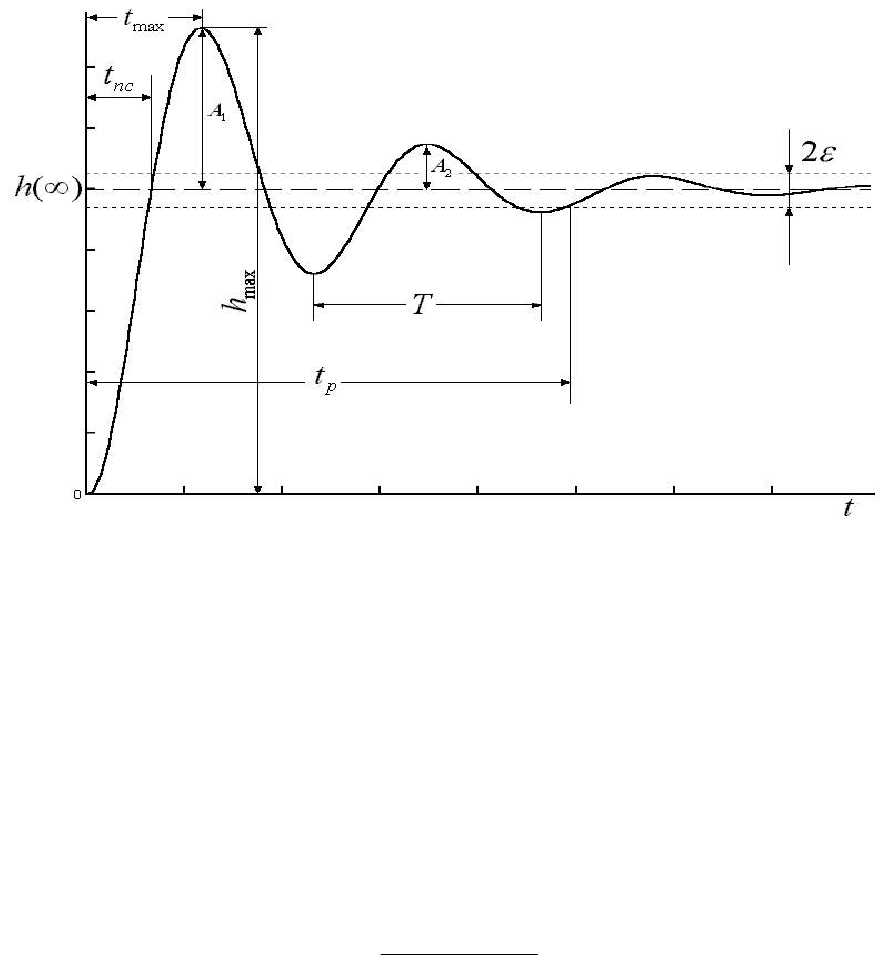
176
Рис. 6.9
К основным показателям характеристики
()ht
относятся перерегулиро-
вание
σ
и время регулирования
р
t
.
Перерегулирование
σ
определяется максимальным отклонением
управляемой величины от ее установившегося значения
)(∞h
, выраженном
в % к
)(∞h
:
%100
)(
)(
max
⋅
∞
∞−
=
h
hh
σ
. (6.8)
Обычно,
3010 ÷=
σ
%, иногда
10
<
σ
%, а иногда недопустимо со-
всем.
Время регулирования
р
t
– время, по истечении которого отклонение
характеристики
()ht
от установившегося значения
)(
∞
h
становится и остает-
ся меньше зоны нечувствительности системы
(0,01 0,05) ( )h
δ
=
÷∞
. Этот
показатель характеризует скорость протекания переходного процесса. Если
кривая переходного процесса монотонна, то этот показатель является един-
ственным.
177
Кроме основных существует и ряд дополнительных показателей каче-
ства. К таким показателям относят:
- время первого согласования переходного процесса
пс
t
– время, по ис-
течении которого управляемая величина первый раз достигает своего устано-
вившегося значения (также характеризует скорость протекания процесса в
начальный период);
- частоту колебаний
T/2
π
ω
=
, где
T
- период колебаний;
- число колебаний
к
n
за время регулирования
р
t
(обычно
к
12n
=
÷
,
иногда
43 ÷
, а иногда и вовсе недопустимо);
- степень затухания
1
21
A
AA
−
=
ψ
, равная отношению разности
двух смежных амплитуд к первой из них (интенсивность затухания считается
удовлетворительной, если
0,75 0,95
ψ
=
÷
;
- время достижения первого максимума
max
t
.
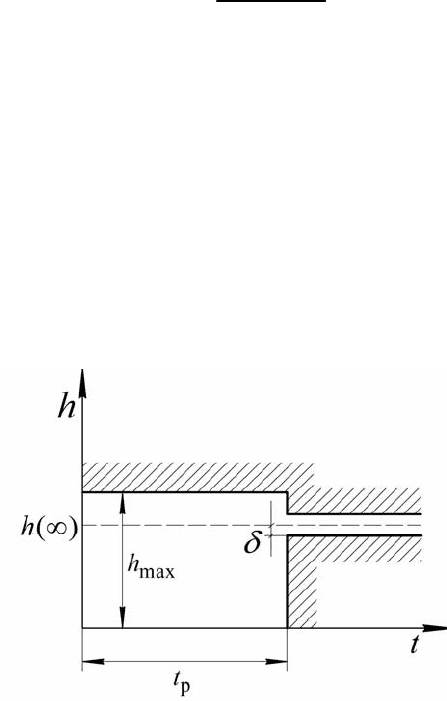
Система обладает необходимым качеством, если удовлетворяет задан-
ным показателям качества, а переходный процесс не выходит из области до-
пустимых значений(см. рис. 6.10).
Рис. 6.10
В случае оценки качества процессов управления по каналу возмущаю-
щего воздействия могут использоваться все перечисленные показатели за ис-
178
ключением перерегулирования. Этот показатель можно заменить непосред-
ственно максимальным значением
max,f
h
:
Косвенные показатели качества определяются без построения пере-
ходных процессов и подразделяются на несколько групп:
- корневые показатели;
- частотные показатели;
- интегральные показатели.
Корневые показатели.
Характер переходных процессов САУ по определенному входу полно-
стью определяется соответствующей передаточной функцией
)(sW
. Если
числитель этой функции не имеет нулей, т.е. представляет собой постоянную
величину, то в соответствии с формулой разложения Хевисайда особенности
переходной характеристики можно оценить по полюсам
)(sW
, т.е. по кор-
ням характеристического уравнения системы
)(sA
. Для этого на комплексной
плоскости выделяется область, в которой располагаются все корни уравнения
0)( =sA
. Обычно эта область имеет форму трапеции (см. рис. 6.11).
Рис. 6.11
При этом на сторонах и основаниях этой трапеции располагается хотя
бы по одному корню.
Основное влияние на длительность переходных процессов оказывают
корни, расположенные ближе других к мнимой оси, т.к. они дают наиболее
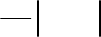
179
медленно затухающие составляющие. Действительная часть такого корня на-
зывается степенью устойчивости
α
.
Составляющая, определяемая степенью устойчивости, записывается
для случая вещественного корня
i
p
α
=
−
в виде:
t
ii
hCe
α
−
=
,
и для случая пары комплексно-сопряженных корней
,1jj
p
j
α
β
+
=− ±
в ви-
де:
sin
t
jj
hC te
α
β
−
=
.
Тогда, приняв
0,05 ( )h
ε
=⋅∞
, можно получить зависимость:
р
1
lnt
ε
α
≤
, (6.9)
где знак равенства относится к случаю вещественного корня.
Основное влияние на колебательные свойства переходных процессов
оказывает пара комплексно сопряженных корней, для которых отношение
/ tg
β
α
ϕμ
==
является наибольшим. Величину
μ
называют колебательно-
стью САУ. При увеличении
μ
возрастает число колебаний
к
n
и возрастает
перерегулирование
σ
.
По значению колебательности
μ
можно определить приближенное
значение перерегулирования переходной характеристики при условии распо-
ложения пары комплексно сопряженных корней ближе остальных к мнимой
оси, воспользовавшись соотношением:
/
e
π
μ
σ
−
≤
. (6.10)
Последняя оценка является несколько завышенной и реальный процесс
может иметь значительно лучшее качество.
Пример 6.4.
САУ имеет передаточную функцию вида:

180
432
1
()
0,0004 0,012 0,107 0,465 1
Ws
ssss
=
+
+++
Определить приближенные оценки прямых показателей качества.
Решение.
Корни характеристического уравнения САУ имеют вид:
43
2,1
jp
±
−
=
;
8
3
−=p
;
10
4
−=p
.
Следовательно:
3
α
=
;
33,13/4
≈
=
μ
.
Тогда
р
11 3
ln ln 0, 05 1
33
tc
ε
α
≤= ≈=
;
/1,33
9, 4%e
π
σ
−
≤≈
.
Действительные значения показателей составляет:
р
1, 2 2tc=
и
%6=
σ
.
***
В заключение заметим, что можно показать, что в системе любого по-
рядка наиболее быстрый апериодический переходный процесс имеет место,
когда все
n
корней равны между собой. Максимальное быстродействие сис-
темы достигается при небольшой колебательности (
%10
≤
σ
). Для этого все
комплексные корни (и один действительный при
n
нечетном) должны рас-
полагаться на одинаковом расстоянии
α
от мнимой оси, а мнимые части
должны образовывать арифметическую прогрессию с разностью
1
β
β
=
Δ
.
Причем, для каждого порядка уравнения существует оптимальное отноше-
ние
/
β
α
Δ
: для 2-го порядка оно равно 1; для 3-го – 1,45; 4-го – 0,79; 5-го
– 1,5.
Частотные показатели.
Частотные показатели качества, определяемые по частотным характе-
ристикам САУ, получили наибольшее распространение на практике. Это
объясняется тем, что практически любой сигнал, действующий на систему,
может быть представлен в виде суммы гармоник (разложен в ряд Фурье). По-
этому, изучив прохождение гармонических сигналов через САУ в диапазоне
